[논문리뷰] Fine-Tuning Image-Conditional Diffusion Models is Easier than You Think
WACV 2025 (Oral). [Paper] [Page] [Github]
Gonzalo Martin Garcia, Karim Abou Zeid, Christian Schmidt, Daan de Geus, Alexander Hermans, Bastian Leibe
RWTH Aachen University | Eindhoven University of Technology
17 Sep 2024
Introduction
최근 논문들에서는 깊이 예측을 조건부 이미지 생성으로 생각하여 monocular depth estimation을 위한 대규모 diffusion model을 적용하는 방안을 제안했다. 그 결과 모델은 우수한 성능을 보이며 매우 높은 수준의 디테일을 제공한다. 그러나 inference 과정에서 대규모 신경망에 대한 여러 차례의 평가를 수행해야 하기 때문에 속도가 느린 경향이 있다.
본 논문에서는 일반적인 믿음과는 달리, Marigold와 같은 조건부 latent diffusion model은 single-step inference로 합리적인 예측 결과를 도출할 수 있어야 한다고 주장한다. 저자들이 Marigold의 동작을 조사한 결과, few-step inference에서 Marigold의 저조한 성능은 inference 파이프라인의 심각한 결함 때문임을 발견했다. 이 버그는 일반적인 diffusion model 관련 논문에서 이미 보고되었지만, Marigold와 같은 이미지 조건부 방법에서 특히 심각하다. 특히, 본 논문의 결과는 기존 논문들이 잘못된 inference 결과로 인해 잘못된 결론을 도출했을 가능성이 있음을 시사한다.
Inference 파이프라인을 약간 수정하면 Marigold와 비슷한 모델은 multi-step 앙상블 inference와 비슷한 single-step 성능을 얻을 수 있으며, 200배 이상 빠르다. 실제로 이 버그 수정을 통해 diffusion 기반 깊이 추정 속도가 SOTA 모델과 비슷해져 다음과 같은 추가 개선을 위한 흥미로운 길이 열렸다.
- Single-step 모델은 여러 네트워크 호출을 통해 backpropagation할 필요가 없으므로 task별 end-to-end fine-tuning을 효율적으로 수행할 수 있다.
- Pseudo-label을 사용한 self-training과 같은 고급 기술을 이제 사전 학습된 diffusion model에도 효율적으로 적용할 수 있다.
저자들은 scale- and shift- invariant loss를 사용하여 monocular 이미지에 대한 deterministic affine-invariant depth estimator로 Marigold를 end-to-end fine-tuning했다. 놀랍게도 이 모델은 Marigold의 최적 구성보다 성능이 우수했다. 표면 normal 추정의 경우에도 유사한 결과를 얻었다. Task별 loss를 적용한 end-to-end fine-tuning은 더 많은 데이터로 학습된 더 복잡한 아키텍처보다 성능이 우수했다.
Stable Diffusion (SD)을 deterministic feed-forward model로 직접 fine-tuning하는 가장 간단한 baseline조차도 Marigold나 기타 diffusion 기반 깊이 추정 및 normal 추정 방법보다 성능이 우수하였다. 즉, diffusion 기반 깊이 추정 및 normal 추정 방법은 느릴 필요가 없으며, 깊이 추정을 조건부 이미지 생성으로 생각하는 것이 단순한 end-to-end fine-tuning보다 효과적이지 않다.
Method
1. Fixing Single-Step Inference

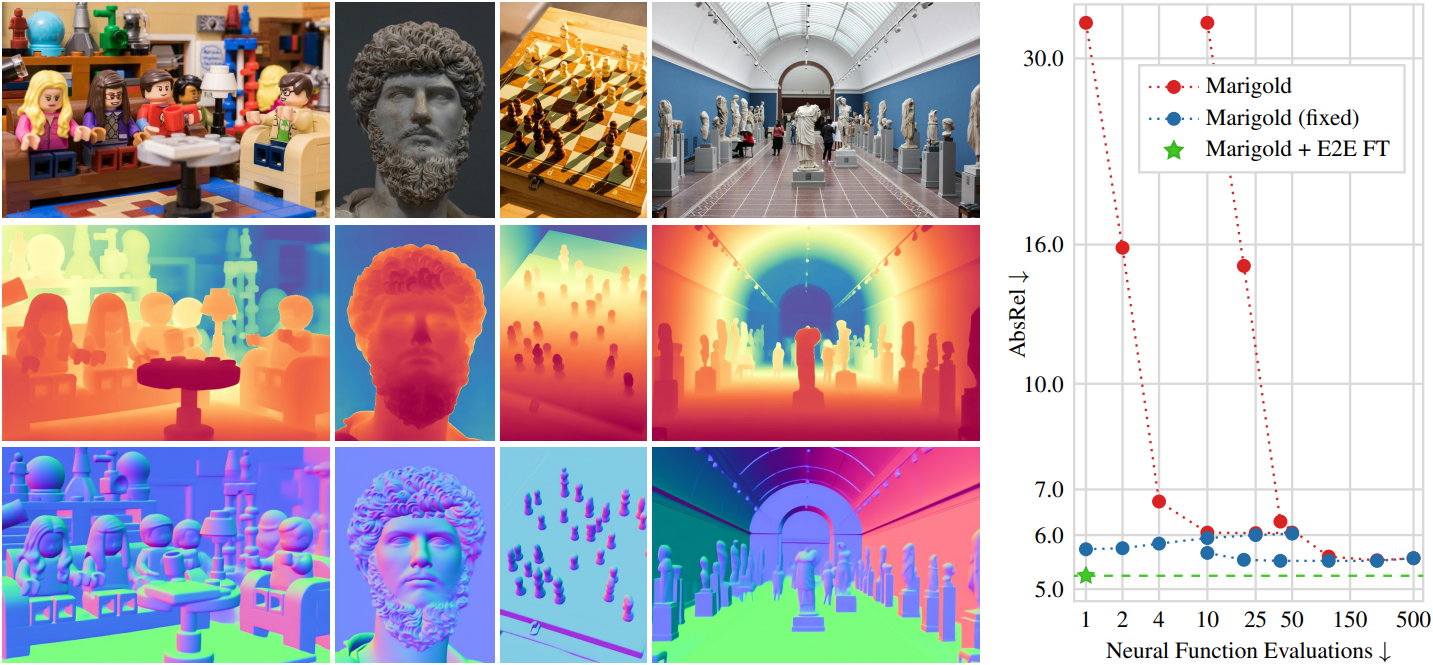
저자들은 Marigold의 inference 시의 동작을 분석해 보았다. 위 그림의 (b)는 Marigold의 기본 50-step inference 시에 step에 대한 표준 편차를 보여준다. 거의 모든 픽셀에서 매우 작은 차이가 관찰되었는데, 이는 inference 중 모델이 예측을 거의 변경하지 않음을 나타낸다. 이는 50-step의 첫 번째 예측이 이미 최종 출력과 거의 일치함을 의미한다. Single-step 출력은 50-step의 첫 번째 step과 유사할 것으로 예상되지만, 위 그림의 (c)에서 볼 수 있듯이 첫 번째 step의 출력은 순수한 noise에 해당한다.
이러한 불일치는 Marigold에서 사용하는 inference 스케줄러 구현의 결함으로 인해 발생한다. 이 결함으로 인해 모델은 timestep과 noise의 불일치한 쌍을 수신하게 되어, 결과적으로 무의미한 예측 결과를 도출한다. 특히, single-step 예측의 경우, 모델은 거의 완벽한 depth map을 나타내는 timestep 인코딩을 수신하지만, 실제 입력은 순수한 noise이다. 즉, 모델은 예상보다 훨씬 많은 noise를 수신하고, noise를 거의 그대로 전달한다.
결함을 수정하는 것은 간단하다. Timestep을 noise 레벨에 맞춰 조정하면 된다. 이를 위해 이미지 생성 모델 논문에서 제안된 trailing 설정을 사용할 수 있다. 이 설정은 이미지 생성 성능에는 약간의 개선만 제공했지만, Marigold와 같은 모델의 single-step inference에는 매우 중요하다.
위 그림의 (c)와 (d)는 결함이 있는 inference 스케줄과 고정된 inference 스케줄을 각각 사용하여 동일한 모델의 출력을 비교한 것이다. 고정된 inference 프로세스는 합리적인 예측을 생성하는 반면, 원본은 그렇지 않음이 분명하다.
2. End-to-End Fine-Tuning of LDMs
Diffusion 기반 깊이 추정 모델은 전반적으로 우수한 성능과 정확한 디테일을 보여주지만, 흐릿하거나 과도하게 선명해진 출력과 같은 아티팩트도 발생한다. 이는 diffusion loss 때문일 수 있는데, 이는 모델이 원하는 다운스트림 task가 아닌 denoising task에 대해 학습되었기 때문이다.
이 문제를 해결하기 위해 diffusion model을 end-to-end 방식으로 직접 fine-tuning한다. 합리적인 single-step 예측 없이 diffusion model을 end-to-end fine-tuning하려면 여러 네트워크 호출을 통한 backpropagation 연산이 필요하며, 이는 수억 개의 파라미터를 가진 모델의 경우 계산적으로 불가능하다.
저자들은 diffusion 학습 단계에서 사용된 수정된 UNet을 계속 학습시켰다. 그러나 더 이상 timestep $t$를 샘플링하지 않고 대신 $t = T$로 고정하여 항상 single-step 예측을 위한 모델을 학습시켰다. 또한, noise를 0으로 대체하고 RGB latent만 모델을 통해 전달하였다. Diffusion 학습 동안 $t = T$는 $\textbf{v}$-parameterization에 따라
\[\begin{equation} \textbf{v}_T^\ast = \sqrt{\vphantom{1} \bar{\alpha}_T} \boldsymbol{\epsilon} - \sqrt{1 - \bar{\alpha}_T} \textbf{z}^\ast \end{equation}\]에 해당한다. \(\bar{\alpha}_T \approx 0\)인 경우 모델은 순수한 noise를 깨끗한 예측 \(\textbf{z}^\ast\)로 변환하도록 학습되어 효과적으로 single-step 예측을 수행한다. UNet의 출력은
\[\begin{equation} \hat{\textbf{z}}_0 = \sqrt{\vphantom{1} \bar{\alpha}_t} \textbf{z}_t - \sqrt{1 - \bar{\alpha}_t} \hat{\textbf{v}}_\theta ([\textbf{z}_t, \textbf{x}], t) \end{equation}\]를 사용하여 latent depth map 예측으로 변환할 수 있으며, 이는 고정된 VAE 디코더를 사용하여 디코딩되고 GT depth map과 비교된다. Marigold는 MSE loss를 사용하여 GT depth map의 latent를 일치시키도록 학습하는 반면, 저자들은 디코딩된 depth map의 예측을 최적화하였다. 결과적으로 생성된 feed-forward model은 deterministic하며, task별 loss를 사용하여 end-to-end로 학습된다.
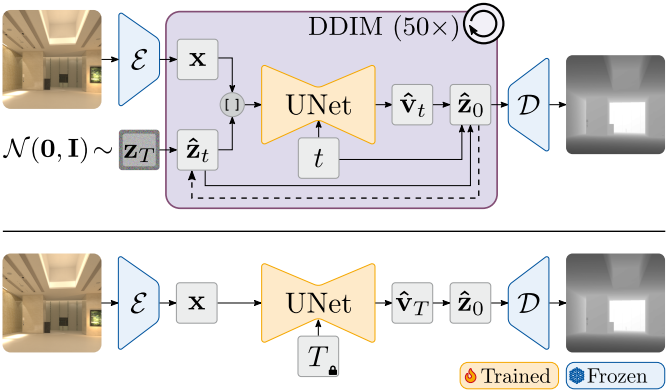
위 그림에서 볼 수 있듯이, inference 과정도 deterministic하게 single-step으로 변경된다.
Monocular depth estimation의 경우, scale- and shift- invariant loss를 사용한다. 구체적으로, GT depth map $\textbf{d}^\ast$와 예측된 depth map $\textbf{d}$ 사이에 least-squares fitting을 수행하여 scale 값 $s$와 shift 값 $t$를 추정한다. 정렬된 예측은 \(\hat{\textbf{d}} = s \textbf{d} + t\)로 주어지며, loss function은 다음과 같이 정의된다.
\[\begin{equation} \mathcal{L}_D = \frac{1}{HW} \sum_{i,j} \vert d_{i,j}^\ast - \hat{d}_{i,j} \vert \end{equation}\]표면 normal 추정의 경우, GT normal $n^\ast$과 예측된 normal $\hat{n}$ 사이의 각도를 기반으로 하는 loss를 사용한다.
\[\begin{equation} \mathcal{L}_N = \frac{1}{HW} \sum_{i,j} \textrm{arccos} \left( \frac{n_{i,j}^\ast \cdot \hat{n}_{i,j}}{\| n_{i,j}^\ast \| \| \hat{n}_{i,j} \|} \right) \end{equation}\]Experiments
- 데이터셋: Hypersim, Virtual KITTI 2 (Marigold와 동일)
- 구현 디테일
- Marigold의 hyperparmeter를 따름
- base model: 깊이 추정의 경우 Marigold의 checkpoint를 사용, normal 추정은 Marigold와 동일한 방법으로 학습
- optimizer: AdamW
- learning rate: $3 \times 10^{-5}$ (exponential decay, 100-step warm-up)
- effective batch size: 32 (batch size = 2, accumulation step = 16)
- GPU: NVIDIA H100 1개로 약 3일 소요
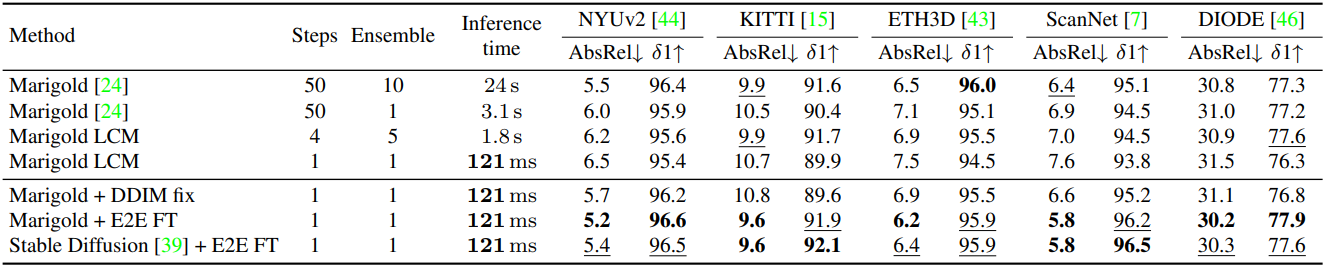
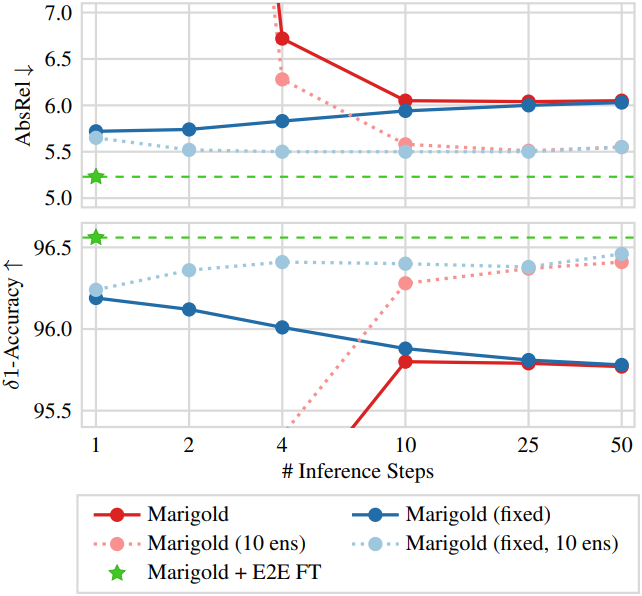
다음은 Marigold와 깊이 추정 성능을 비교한 결과이다.
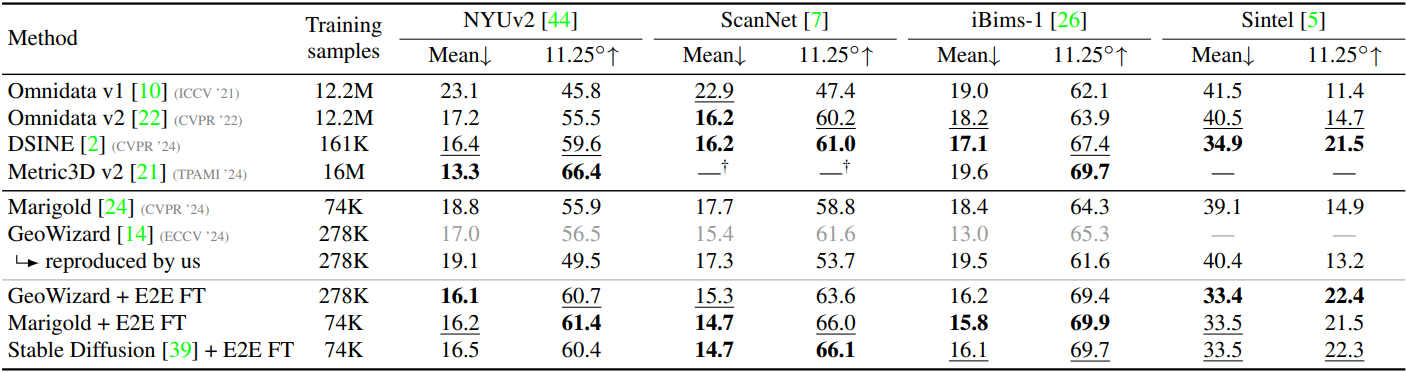
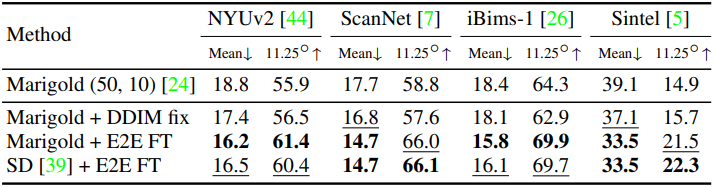
다음은 Marigold와 normal 추정 성능을 비교한 결과이다.
다음은 GeoWizard와 깊이 추정 성능을 비교한 결과이다.

다음은 end-to-end fine-tuning을 Marigold와 GeoWizard에 적용한 모델을 Marigold와 비교한 예시들이다.

다음은 noise 종류에 따른 깊이 추정 성능을 비교한 결과이다.

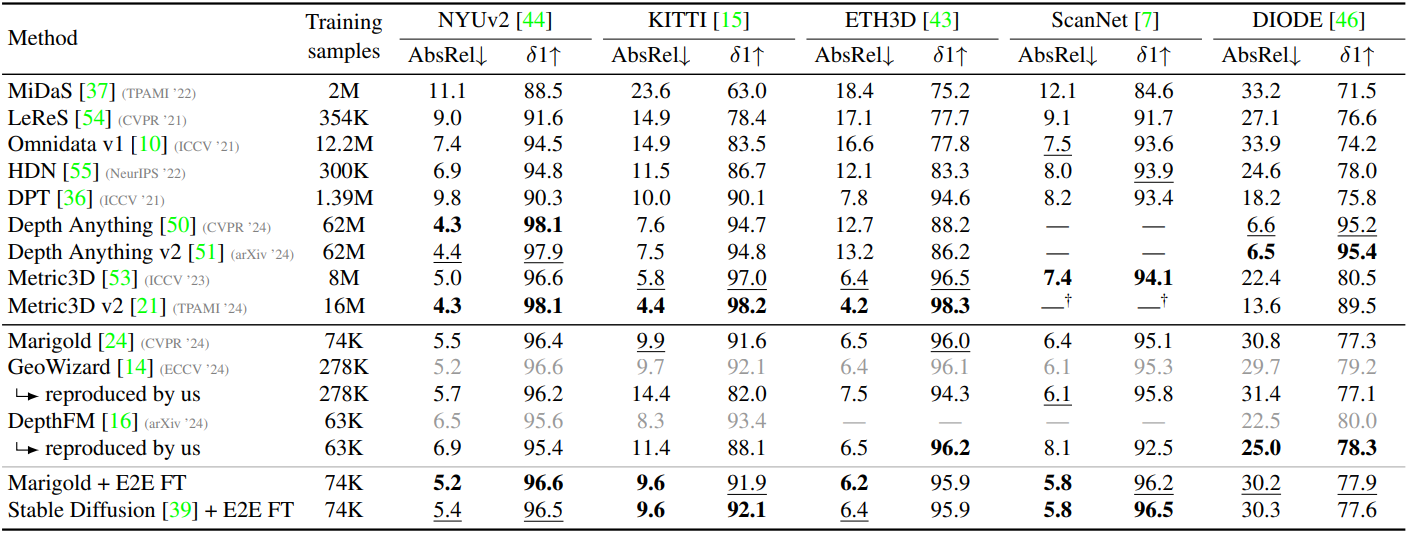
다음은 SOTA 깊이 추정 모델과의 비교 결과이다.
다음은 SOTA normal 추정 모델과의 비교 결과이다.