[논문리뷰] DUSt3R: Geometric 3D Vision Made Easy

CVPR 2024. [Paper] [Page] [Github]
Shuzhe Wang, Vincent Leroy, Yohann Cabon, Boris Chidlovskii, Jerome Revaud
Aalto University | Naver Labs Europe
21 Dec 2023

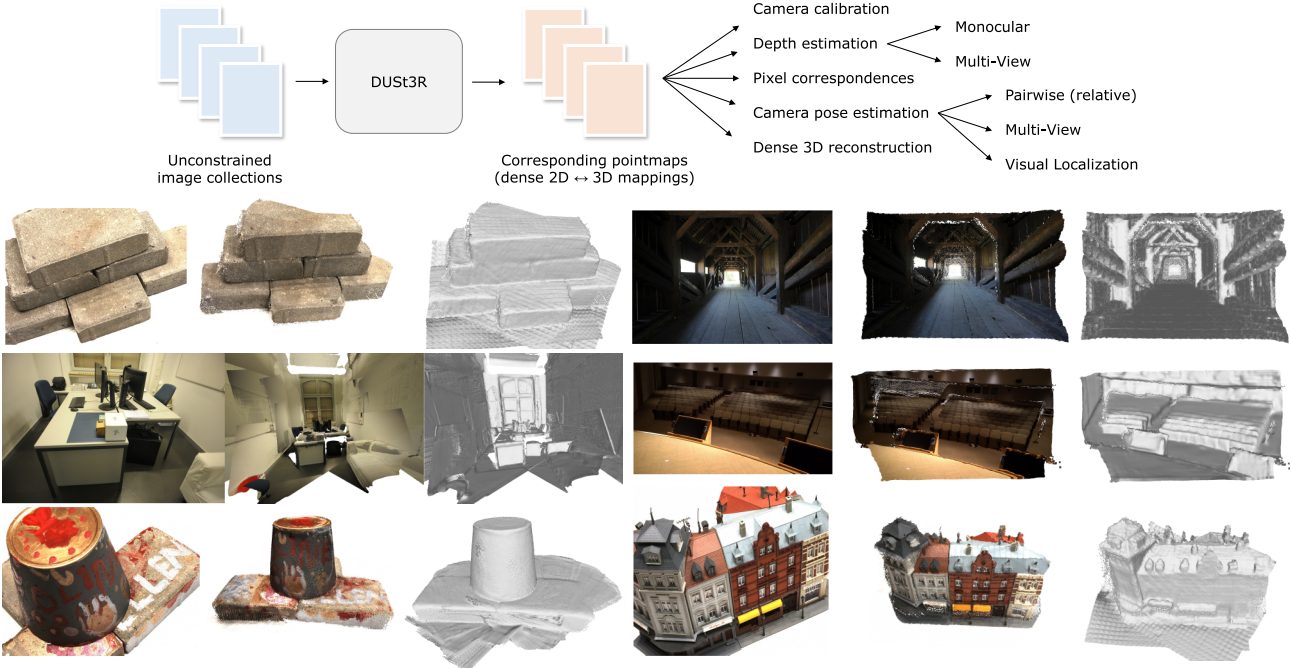
Introduction

본 논문에서는 calibration되지 않고 포즈를 모르는 카메라에서 Dense Unconstrained Stereo 3D Reconstruction을 위한 근본적으로 새로운 접근 방식인 DUSt3R를 제시하였다. 주요 구성 요소는 장면이나 카메라에 대한 어떠한 사전 정보 없이 한 쌍의 이미지에서만 dense하고 정확한 장면 표현을 예측할 수 있는 네트워크이다. 장면 표현은 풍부한 속성을 가진 3D pointmap을 기반으로 하며, pointmap은 장면 형상, 픽셀과 장면 포인트 간의 관계, 두 시점 간의 관계를 동시에 나타낸다. 이 출력만으로도 거의 모든 장면 파라미터를 간단히 추출할 수 있다. 이것이 가능한 것은 네트워크가 입력 이미지와 결과 3D pointmap을 공동으로 처리하여 2D 구조를 3D 모양과 연관시키는 방법을 학습하고 여러 개의 minimal problem들을 동시에 해결하기 때문이다.

DUSt3R는 단순 regression loss를를 사용하여 fully-supervised 방식으로 학습되며, ground-truth가 합성적으로 생성되거나 SfM에서 재구성되거나 전용 센서로 캡처되는 대규모 공개 데이터셋을 활용한다. 저자들은 task별 모듈을 통합하는 트렌드에서 벗어나, 강력한 사전 학습의 이점을 얻을 수 있는 transformer 아키텍처를 기반으로 하는 완전히 데이터 기반 전략을 채택하였다. 네트워크는 MVS에서 일반적으로 활용되는 것과 유사한 강력한 geometric prior와 shape prior를 학습한다.

여러 이미지 쌍의 예측을 융합하기 위해 pointmap에 대한 bundle adjustment(BA)를 수행하여 전체 규모의 MVS를 달성한다. 저자들은 BA와 달리 reprojection error를 최소화하지 않는 global alignment 절차를 도입하였다. 대신 3D 공간에서 카메라 포즈와 형상 정렬을 직접 최적화하는데, 이는 빠르고 실제로 뛰어난 수렴을 보여준다.

Method

Pointmap

3D 포인트의 dense한 2D 필드를 pointmap $X \in \mathbb{R}^{W \times H \times 3}$라 하자. 해상도가 $W \times H$인 RGB 이미지 $I$에 대하여 $X$는 이미지 픽셀과 3D 포인트 사이에 일대일 매핑을 형성한다. 즉, 모든 픽셀 좌표 $(i, j)$에 대해 $I_{i,j} \leftrightarrow X_{i,j}$이다. 여기서는 각 카메라 광선이 하나의 3D 포인트에 도달한다고 가정한다. 즉, 반투명 표면의 경우는 무시한다.

Cameras and scene

카메라 intrinsic $K \in \mathbb{R}^{3 \times 3}$이 주어지면, ground-truth depth map $D \in \mathbb{R}^{W \times H}$에서 pointmap $X$를 쉽게 얻을 수 있다.

\[\begin{equation} X_{i,j} = K^{-1} [i D_{i,j}, j D_{i,j}, D_{i,j}]^\top \end{equation}\]

여기서, $X$는 카메라 좌표 프레임에서 표현된다. 카메라 $m$의 좌표 프레임에서 표현된 카메라 $n$의 pointmap $X^n$을 $X^{n,m}$이라 하면, $X^{n,m}$은 다음과 같이 계산된다.

\[\begin{equation} X^{n,m} = P_m P_n^{-1} h (X^n) \end{equation}\]

($P_m, P_n \in \mathbb{R}^{3 \times 4}$는 이미지 $n$과 $m$에 대한 world-to-camera 포즈, $h : (x, y, z) \rightarrow (x, y, z, 1)$은 homogeneous mapping)

1. Network Architecture

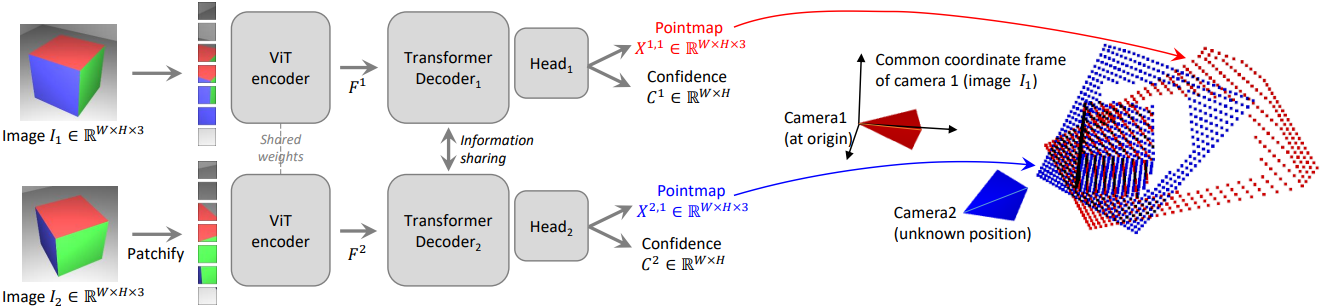
네트워크 $\mathcal{F}$의 아키텍처는 CroCo에서 영감을 받았다. $\mathcal{F}$는 각 이미지당 하나씩 총 두 개의 동일한 브랜치로 구성되어 있으며, 각각 이미지 인코더, 디코더, regression head로 구성된다. 두 개의 입력 이미지는 먼저 동일한 가중치를 사용하는 ViT 인코더로 인코딩되어 두 개의 토큰 표현 $F^1$과 $F^2$가 생성된다.

\[\begin{aligned} F^1 &= \textrm{Encoder} (I^1) \\ F^2 &= \textrm{Encoder} (I^2) \end{aligned}\]

그런 다음 네트워크는 디코더에서 두 가지 모두를 공동으로 추론한다. CroCo와 유사하게 디코더는 cross-attention을 갖춘 일반 transformer 네트워크이다. 따라서 각 디코더 블록은 순차적으로 self-attention을 수행한 다음 cross-attention을 수행하고 마지막으로 토큰을 MLP에 공급한다.

중요한 점은 디코더 간에 정보가 지속적으로 공유된다는 것이며, 이는 적절하게 정렬된 pointmap을 출력하기 위해 필수적이다. 즉, 각 디코더 블록은 다른 브랜치의 토큰에 attention을 한다.

\[\begin{aligned} G_i^1 &= \textrm{DecoderBlock}_i^1 (G_{i-1}^1, G_{i-1}^2) \\ G_i^2 &= \textrm{DecoderBlock}_i^2 (G_{i-1}^2, G_{i-1}^1) \end{aligned}\]

($\textrm{DecoderBlock}_i^v$는 브랜치 $v \in \{1,2\}$의 $i$번째 블록)

$G_0^1$과 $G_0^2$는 각각 인코더 토큰 $F^1$과 $F^2$로 초기화된다. 마지막으로 각 브랜치에서 별도의 regression head가 디코더 토큰 세트를 가져와 pointmap과 신뢰도 맵을 출력한다.

\[\begin{aligned} X^{1,1}, C^{1,1} &= \textrm{Head}^1 (G_0^1, \ldots, G_B^1) \\ X^{2,1}, C^{2,1} &= \textrm{Head}^2 (G_0^2, \ldots, G_B^2) \end{aligned}\]

출력 pointmap $X^{1,1}$과 $X^{2,1}$은 모르는 scale factor를 포함한다. 또한, 아키텍처는 기하학적 제약을 명시적으로 적용하지 않기 때문에 pointmap이 반드시 물리적으로 타당한 카메라 모델과 일치하지 않는다. 오히려, 저자들은 네트워크가 기하학적으로 일관된 pointmap만 포함하는 학습 세트에서 모든 관련 prior들을 학습하도록 하였다. 이를 통해 궁극적으로 기존 task별 아키텍처가 달성할 수 있는 것을 능가할 수 있다.

2. Training Objective

3D Regression loss

DUSt3R의 유일한 loss는 3D 공간에서의 regression에 기반을 둔다. GT pointmap을 $\bar{X}^{1,1}$과 $\bar{X}^{2,1}$라 하고 GT가 정의된 두 개의 유효 픽셀 세트를 $\mathcal{D}^1$, $\mathcal{D}^2$라 하자. 뷰 $v \in \{1, 2\}$에서 유효 픽셀 $i \in \mathcal{D}^v$에 대한 regression loss는 간단히 유클리드 거리로 정의된다.

\[\begin{equation} \ell_\textrm{regr}(v, i) = \| \frac{1}{z} X_i^{v,1} - \frac{1}{\bar{z}} \bar{X}_i^{v,1} \| \\ \end{equation}\]

예측과 GT 간의 스케일 모호성을 처리하기 위해 예측 pointmap과 GT pointmap을 각각 scaling factor $z$와 $\bar{z}$로 정규화한다.

\[\begin{aligned} z &= \textrm{norm} (X^{1,1}, X^{2,1}) \\ \bar{z} &= \textrm{norm} (\bar{X}^{1,1}, \bar{X}^{2,1}) \end{aligned}\]

이는 단순히 모든 유효 포인트에서 원점까지의 평균 거리를 나타낸다.

\[\begin{equation} \textrm{norm}(X^1, X^2) = \frac{1}{\vert \mathcal{D}^1 \vert + \vert \mathcal{D}^2 \vert} \sum_{v \in \{1,2\}} \sum_{i \in \mathcal{D}^v} \| X_i^v \| \end{equation}\]

Confidence-aware loss

실제로는 저자들의 가정과는 달리 하늘이나 반투명 물체와 같이 정의되지 않은 3D 포인트가 있다. 보다 일반적으로, 이미지의 일부 부분은 일반적으로 다른 부분보다 예측하기 어렵다. 따라서 네트워크가 이 특정 픽셀에 대해 가지고 있는 신뢰도를 나타내는 각 픽셀에 대한 점수를 예측하는 방법을 공동으로 학습시킨다. 최종 loss는 다음과 같다.

\[\begin{equation} \mathcal{L}_\textrm{conf} = \sum_{v \in \{1,2\}} \sum_{i \in \mathcal{D}^v} C_i^{v,1} \ell_\textrm{regr} (v,i) - \alpha \log C_i^{v,1} \end{equation}\]

($C_i^{v,1}$는 픽셀 $i$에 대한 신뢰도 점수, $\alpha$는 정규화 항을 제어하는 hyperparameter)

항상 양의 신뢰도를 보장하기 위해 일반적으로 $C_i^{v,1} = 1 + \exp \tilde{C}_i^{v,1} > 1$로 정의한다. 이 loss로 네트워크 $\mathcal{F}$를 학습시키면 명시적인 supervision 없이도 신뢰도 점수를 추정할 수 있다.

3. Downstream Applications

출력 pointmap의 풍부한 속성 덕분에 비교적 쉽게 다양하고 편리한 연산들을 수행할 수 있다.

Point matching

3D pointmap 공간에서 nearest neighbor (NN) search를 통해 두 이미지의 픽셀 간의 대응 관계를 찾을 수 있다. 일반적으로 이미지 $I^1$과 $I^2$ 간의 상호 대응 관계 $\mathcal{M}_{1,2}$를 찾는다.

\[\begin{equation} \mathcal{M}_{1,2} = \{(i,j) \, \vert \, i = \textrm{NN}_1^{1,2} (j), j = \textrm{NN}_1^{2,1} (i) \} \\ \textrm{where} \quad \textrm{NN}_k^{n,m} (i) = \underset{j \in \{0, \ldots, WH\}}{\arg \min} \| X_j^{n,k} - X_i^{m,k} \| \end{equation}\]

Recovering intrinsics

Pointmap $X^{1,1}$은 $I^1$의 좌표 프레임으로 표현된다. 따라서 간단한 최적화 문제를 풀어 카메라 intrinsic을 추정하는 것이 가능하다. 본 논문에서는 principal point가 대략 중앙에 있고 픽셀이 정사각형이라고 가정하므로 초점 거리 $f_1^\ast$만 추정하면 된다.

\[\begin{equation} f_1^\ast = \underset{f_1}{\arg \min} \sum_{i=0}^W \sum_{j=0}^H C_{i,j}^{1,1} \| (i - \frac{W}{2}, j - \frac{H}{2}) - f_1 \frac{(X_{i,j,0}^{1,1} - X_{i,j,1}^{1,1})}{X_{i,j,2}^{1,1}} \| \end{equation}\]

Iterative solver를 몇 번의 사용하면 최적의 $f_1^\ast$을 찾을 수 있다. 두 번째 카메라의 초점 거리 $f_2^\ast$의 경우 $(I^2, I^1)$에 대한 inference를 수행하고 $X^{1,1}$ 대신 $X^{2,2}$를 사용하여 위의 식을 풀면 된다.

Relative pose estimation

상대적 포즈 추정은 여러 가지 방식으로 사용할 수 있다. 한 가지 방법은 위에서 설명한 대로 2D 매칭을 수행하고 intrinsic을 복구한 다음 Epipolar 행렬을 추정하고 상대적 포즈를 계산하는 것이다.

더 직접적인 방법은 Procrustes alignment를 사용하여 pointmap $X^{1,1} \leftrightarrow X^{1,2}$ 또는 $X^{2,2} \leftrightarrow X^{1,2}$를 비교하여 상대적 포즈 $P^\ast = [R^\ast \vert t^\ast]$를 구하는 것이다.

\[\begin{equation} R^\ast, t^\ast = \underset{\sigma, R, t}{\arg \min} \sum_i C_i^{1,1} C_i^{1,2} \| \sigma (RX_i^{1,1} + t) - X_i^{1,2} \|^2 \end{equation}\]

이는 closed-form으로 해를 찾을 수 있다. Procrustes alignment는 노이즈와 outlier에 민감하다. 더 강력한 방법은 결국 PnP를 사용한 RANSAC에 의존하는 것이다.

Absolute pose estimation (Visual localization)

쿼리 이미지를 $I^Q$, 레퍼런스 이미지를 $I^B$라 하자. 먼저 $I^Q$에 대한 intrinsic을 $X^{Q,Q}$에서 추정한다. 그런 다음, 두 가지 방법을 사용할 수 있다.

$I^Q$와 $I^B$사이의 2D correspondence를 구한 후, $I^Q$에 대한 2D-3D correspondencef를 생성하고 PnP-RANSAC를 실행한다.
$I^Q$와 $I^B$ 사이의 상대적 포즈를 구한 후, $X^{B,B}$와 $I^B$의 GT pointmap 사이의 scale로 적절하게 스케일링하여 구한 포즈를 world 좌표로 변환한다.

4. Global Alignment

지금까지 제시된 네트워크 $\mathcal{F}$는 한 쌍의 이미지만 처리할 수 있다. 이제 여러 이미지에서 예측된 pointmap을 공통된 3D 공간으로 정렬할 수 있는 전체 장면에 대한 빠르고 간단한 후처리 최적화가 필요하다. 이는 설계상 두 개의 정렬된 포인트 클라우드와 픽셀-3D 매핑을 포함하는 pointmap의 풍부한 콘텐츠 덕분이다.

Pairwise graph

주어진 장면에 대한 이미지 집합 $\{I^1, \ldots, I^N\}$이 주어지면, 먼저 $N$개의 이미지가 vertex $\mathcal{V}$를 형성하고 각 edge $e = (n, m) \in \mathcal{E}$인 connectivity graph $\mathcal{G} (\mathcal{V}, \mathcal{E})$를 구성한다. 이는 이미지 $I^n$과 $I^m$이 일부 시각적 콘텐츠를 공유한다는 것을 나타낸다.

이를 위해 기존의 이미지 검색 방법을 사용하거나, 모든 쌍을 네트워크 $\mathcal{F}$로 전달하고 두 쌍의 평균 신뢰도를 기반으로 중첩된 정도를 측정한 다음 신뢰도가 낮은 쌍을 필터링한다.

Global optimization

Connectivity graph $\mathcal{G}$를 사용하여 모든 카메라 $n = 1, \ldots, N$에 대해 글로벌하게 정렬된 pointmap $\{\chi^n \in \mathbb{R}^{W \times H \times 3}\}$을 복구한다.

먼저 각 이미지 쌍 $e = (n, m) \in \mathcal{E}$에 대해 쌍별 pointmap $X^{n,n}$, $X^{m,n}$과 신뢰도 맵 $C^{n,n}$, $C^{m,n}$을 예측한다. 공통 좌표 프레임에서 모든 쌍별 예측을 회전시키는 것이 목표이므로 각 쌍 $e \in \mathcal{E}$에 연관된 쌍별 포즈 $P_e \in \mathbb{R}^{3 \times 4}$와 scaling $\sigma_e > 0$을 도입한다. 그런 다음, 다음과 같은 최적화 문제를 푼다.

\[\begin{equation} \chi^\ast = \underset{\chi, P, \sigma}{\arg \min} \sum_{e \in \mathcal{E}} \sum_{v \in e} \sum_{i=1}^{HW} C_i^{v,e} \| \chi_i^v - \sigma_e P_e X_i^{v,e} \| \end{equation}\]

아이디어는 주어진 쌍 $e$에 대해 동일한 강체 변환 $P_e$가 두 pointmap $X^{n,e}$와 $X^{m,e}$를 world 좌표 pointmap $\chi^n$과 $\chi^m$에 맞춰야 한다는 것이다. 왜냐하면 $X^{n,e}$와 $X^{m,e}$는 모두 동일한 좌표 프레임에서 표현되기 때문이다.

모든 $e$에 대해 $\sigma_e = 0$이 되는 것을 피하기 위해 $\prod_e \sigma_e = 1$을 적용한다.

Recovering camera parameters

이 프레임워크를 간단하게 확장하면 모든 카메라 파라미터를 복구할 수 있다. 간단히

\[\begin{equation} \chi_{i,j}^n = P_n^{-1} h (K_n^{-1} [i D_{i,j}^n, j D_{i,j}^n, D_{i,j}^n]) \end{equation}\]

으로 대체하면 모든 카메라 포즈 $\{P_n\}$, 관련된 intrinsic $\{K_n\}$과 depth map $\{D_n\}$을 $n = 1, \ldots, N$에 대해 추정할 수 있다.

Discussion

전통적인 bundle adjustment(BA)와 달리 이 글로벌 최적화는 실제로 빠르고 간단하게 수행할 수 있다. 사실, BA가 일반적으로 하는 것처럼 2D projection error들을 최소화하는 것이 아니라 3D projection error들을 최소화한다. 최적화는 gradient descent를 사용하여 수행되며 일반적으로 수백 step 후에 수렴하여 표준 GPU에서 몇 초만 걸린다.

Experiments

데이터셋: Habitat, MegaDepth, ARKitScenes, MegaDepth, Static Scenes 3D, Blended MVS, ScanNet++, CO3D-v2, Waymo
학습 디테일
- 먼저 224$\times$224 해상도에서 학습시킨 후, 긴 쪽이 512인 이미지에서 이어서 학습
- 각 batch마다 이미지 종횡비를 무작위로 선택
- 원하는 종횡비로 crop후에 긴 쪽이 512가 되도록 resize
아키텍처 디테일
- 인코더: Vit-Large
- 디코더: ViT-Base
- head: DPT
- 사전 학습된 CroCo로 가중치 초기화

1. Visual Localization

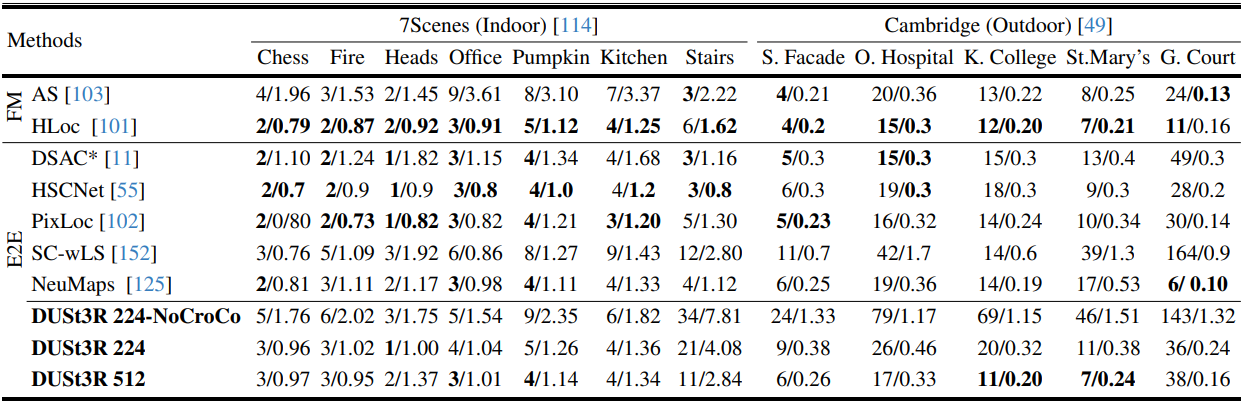
다음은 7Scenes와 Cambridge-Landmarks 데이터셋에서 절대적 카메라 포즈를 추정한 결과이다. (median translation/rotation error (cm/◦)로 비교, FM은 feature matching, E2E는 end-to-end)

2. Multi-view Pose Estimation

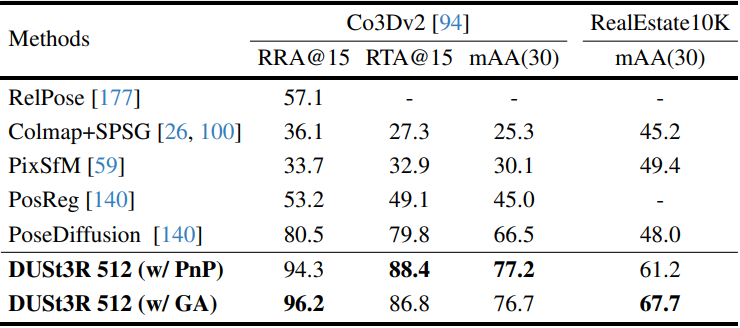
다음은 CO3Dv2와 RealEst10K 데이터셋에서 멀티뷰 포즈를 추정한 결과이다.

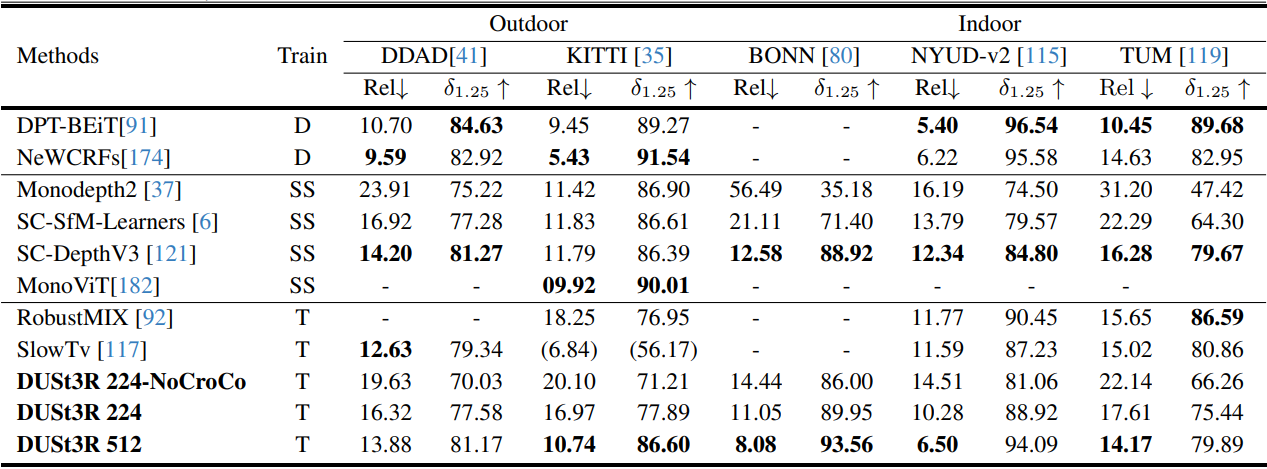
3. Monocular Depth

다음은 monocular depth 추정 결과를 비교한 표이다.

4. Multi-view Depth

다음은 멀티뷰 깊이 추정 결과를 비교한 표이다.

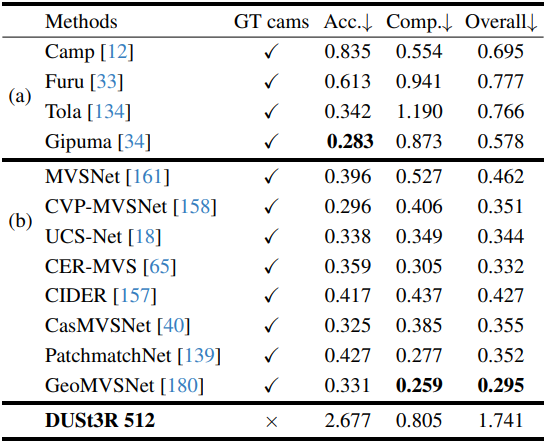
5. 3D Reconstruction

다음은 DTU 데이터셋에서의 MVS 결과이다.

다음은 3D 재구성 예시들이다.

JiYeop Kim