[논문리뷰] Dynamic Dual-Output Diffusion Models
CVPR 2022. [Paper]
Yaniv Benny, Lior Wolf
Tel Aviv University
8 Mar 2022
Introduction
최근까지 잘 최적화된 GAN 모델이 log-likelihood 모델보다 성능이 좋았다. 하지만 이는 DDPM이라는 새로운 log-likelihood 모델이 나오면서 바뀌었다. DDPM은 GAN보다 이미지 품질이 좋으며 학습이 안정적이고 쉽다. DDPM은 noisy한 이미지 $x_t$가 주어졌을 때 덜 noisy한 이미지 $x_{t-1}$을 예측하여 점진적으로 denoise한다. 이 프로세스가 끝나면 굉장히 품질이 높고 다양성이 높은 이미지를 생성한다.
DDPM은 평균 성분 $\mu_{t-1}$의 추정에 의존하는 확률적 denoising process를 통합한다. 이는 신경망 $\mu_\theta (x_t, t)$에 의해 진행된다. 그러나 forward 및 backward 방정식을 통해 이 프로세스는 noise $\epsilon_\theta(x_t, t)$ 또는 원본 이미지 $x_\theta (x_t, t)$를 예측하면 더 잘 공식화됨을 발견했다. 경험적으로 noise를 예측하는 것이 우월하다는 것을 발견했으며, 아직 두 가지 옵션 간의 추가 비교는 아직 수행되지 않았다.
본 논문에서는 저자들은 DDPM의 원래 구현을 다시 검토하고 $x_\theta$보다 $\epsilon_\theta$를 선호하는 것이 상황에 따라 다르며 hyperparameter와 데이터셋에 따라 다르다는 것을 발견했다. 또한 특정 timestep에서 denoising process는 noise 성분 $\epsilon_\theta$를 예측할 때 오류가 적고 다른 경우에는 원래 이미지 $x_\theta$를 더 잘 예측한다.
따라서 저자들은 두 값을 모두 예측하고 각 샘플링 iteration에서 더 신뢰할 수 있는 출력을 적응적으로 선택할 수 있는 모델을 설계하였다. 수정된 모델에 추가된 parameter와 복잡성이 무시해도 될 정도이다. 저자들은 이 방법을 다양한 DDPM 모델에 적용하고 많은 벤치마크에서 이미지 품질(FID)의 현저한 개선을 보여준다. 프레임워크에 대한 이러한 추가는 기존 개선 사항에 영향을 주지 않으며 특히 몇 번의 iteration의 제한으로 샘플링 품질을 향상시킬 수 있다.
Setup
Diffusion model은 점진적인 noising process에 역으로 작동한다. 샘플 $x_0$가 주어질 때 점진적으로 noise를 추가하여 얻은 $x_t$를 생각할 수 있으며 $x_T$는 완전히 파괴되어 사전 정의된 noise 분포의 샘플로 볼 수 있다.
\[\begin{equation} q (x_t \vert x_{t-1}) := \mathcal{N} (x_t; \sqrt{1 - \beta_t} x_{t-1} \beta I) \end{equation}\]가우시안 noise를 추가하도록 선택하였기 때문에 $x_0$에서 바로 임의의 $x_t$를 계산할 수 있어 더 효율적인 학습이 가능하다.
\[\begin{equation} q(x_t \vert x_0) := \mathcal{N} (x_t; \sqrt{\vphantom{1} \bar{\alpha_t}} x_0, (1 - \bar{\alpha_t}) I) \\ a_t := 1 - \beta_t, \quad \bar{\alpha_t} := \prod_{s=1}^t \alpha_s \end{equation}\]이 공식은 더 간단한 제약조건 $\bar{\alpha}_T \approx 0$을 나타내며, 중간 step $x_t$는 다음과 같이 샘플링된다.
\[\begin{equation} x_t = \sqrt{\vphantom{1} \bar{\alpha_t}} x_0 + \sqrt{1 - \bar{\alpha_t}} \epsilon, \quad \epsilon \sim \mathcal{N} (0,I) \end{equation}\]위 식을 이용하면 쉽게 $x_0$를 역으로 구할 수 있다.
\[\begin{equation} x_0 = \frac{1}{\sqrt{\vphantom{1} \bar{\alpha_t}}} (x_t - \sqrt{1 - \bar{\alpha_t}} \epsilon) \end{equation}\]Reverse process는 Markovian process로 신경망으로 parameterize된다.
\[\begin{equation} p_\theta (x_{t-1} \vert x_t) := \mathcal{N} (x_{t-1}; \mu_\theta (x_t, t). \Sigma_\theta (x_t, t)) \end{equation}\]이 모델의 학습은 랜덤한 $t \in [1,T]$를 샘플링하여 SGD로 loss $L_t$를 최소화하여 진행된다.
\[\begin{equation} L_t = D_{KL} (q(x_{t-1} \vert x_t) \| p_\theta (x_{t-1} \vert x_t)) \end{equation}\]목적 함수의 안정성을 위하여 몇몇 중요한 수정이 필요하다. 높은 분산을 가지는 분포 $q(x_{t-1} \vert x_t)$는 더 안정적인 $q(x_{t-1} \vert x_t, x_0)$로 대체되며, 이는 posterior $q(x_{t-1} \vert x_t)$와 forward process $q(x_{t-1} \vert x_0)$의 결합이다.
\[\begin{equation} q (x_{t-1} \vert x_t, x_0) := \mathcal{N} (x_{t-1}; \tilde{\mu}_t (x_t, x_t, t), \tilde{\beta}_t I) \\ \tilde{\mu}_t (x_t, x_t, t) := \frac{\sqrt{\vphantom{1} \bar{\alpha}_{t-1}} \beta_t}{1 - \bar{\alpha}_t} x_0 + \frac{\sqrt{\vphantom{1} \bar{\alpha}_t} (1 - \bar{\alpha}_{t-1}) }{1 - \bar{\alpha}_t} x_t \\ \tilde{\beta}_t := \frac{1 - \bar{\alpha}_{t-1}}{1 - \bar{\alpha}_t} \beta_t \end{equation}\]DDPM 논문에서는 $\Sigma_t$를 상수 $\sigma_t^2$로 고정하는 것이 목적 함수를 최적화하는 데 더 쉽다는 것을 발견했으며, 평균 벡터 $\tilde{\mu}_t$만 예측하면 되도록 목적 함수를 줄일 수 있다.
\[\begin{equation} p_\theta (x_{t-1} \vert x_t) := \mathcal{N} (x_{t-1}; \mu_\theta (x_t, t), \sigma_t^2 I) \end{equation}\]손실 함수는 다음과 같다.
\[\begin{equation} L_t := \frac{1}{2\sigma_t^2} \| \tilde{\mu}_t (x_t, x_0, t) - \mu_\theta (x_t, t) \|^2 \end{equation}\]상수 $\sigma_t$는 $\beta_t$로 선택되며 $\tilde{\beta}_t$를 대신 선택할 수 있다.
추가로, $\mu_\theta$를 직접 예측하는 것은 $x_\theta$로 $x_0$를 예측한 후 $\mu_\theta$를 계산하거나 $\epsilon_\theta$로 $\epsilon$를 예측한 후 $\mu_\theta$를 계산하는 것으로 대체할 수 있다.
\[\begin{equation} \mu_x (x_\theta) := \frac{\sqrt{\vphantom{1} \bar{\alpha}_t} (1 - \bar{\alpha}_{t-1}) }{1 - \bar{\alpha}_t} x_t + \frac{\sqrt{\vphantom{1} \bar{\alpha}_{t-1}} \beta_t}{1 - \bar{\alpha}_t} x_\theta \\ \mu_\epsilon (\epsilon_\theta) := \frac{1}{\sqrt{\vphantom{1} \bar{\alpha_t}}} x_t - \frac{1 - \alpha_t}{\sqrt{1 - \bar{\alpha}_t}\sqrt{\vphantom{1} \bar{\alpha_t}}} \epsilon_\theta \end{equation}\]후자를 사용하는 것이 경험적으로 더 좋으며 새로운 $L_t$를 공식화할 수 있다.
\[\begin{equation} L_t = M_t \| \epsilon - \epsilon_\theta (\underbrace{\sqrt{\vphantom{1} \bar{\alpha}_t} x_0 + \sqrt{1 - \bar{\alpha}_t}\epsilon}_{x_t}, t) \|^2 \\ M_t = \frac{\beta_t^2}{2 \sigma_t^2 \alpha_t (1- \bar{\alpha}_t)} \end{equation}\]DDPM 논문에서는 간단하게 $M_t = 1$로 두었다.
1. Pros and cons for predicting $\epsilon$
Noise를 예측하여 backward process를 구동해야 하는 이유는 여러 가지가 있다. 첫 번째는 항상 noise의 평균이 0이고 분산이 1이며, 모델이 이를 매우 쉽게 학습할 수 있다는 것이다. 두 번째는 이미지 $x_0$가 입력에서 모델의 출력을 빼서 예측되는 residual과 같은 방정식을 제공한다는 것이다. 이는 모델에 zero noise을 예측하거나 작은 $\sqrt{1 - \bar{\alpha_t}}$를 곱하여 입력 정보를 보존하는 옵션을 제공한다. 이 방식은 denoising process가 끝날수록 noise 양이 작아지고 약간의 수정만 필요하기 때문에 점점 더 장점이 커진다.
이 방식의 주요 단점은 $x_t$에서 noise를 뺀 후 결과가 \(\sqrt{\vphantom{1} \bar{\alpha}_t}\)로 스케일링되며 $t$가 큰 경우에서는 매우 작은 값이 될 수 있다는 것이다. 이로 인해 $\epsilon_\theta$의 오차가 작더라도 매우 큰 오차가 발생할 수 있다. 모델이 noise와 유사한 것으로 중간 상태를 수정하도록 제한되기 때문에 이 오차는 전파되며, 이전 iteration에서 존재하지 않는 상태 $x_{t-1}$이 생성된 경우 모델이 이 경로를 수정하기가 어려워진다. 이러한 경우 이전의 잘못된 예측을 되돌리기 위해 여러 번의 iteration이 필요할 수 있다.
이 문제는 아래 그림에서 확인할 수 있다.
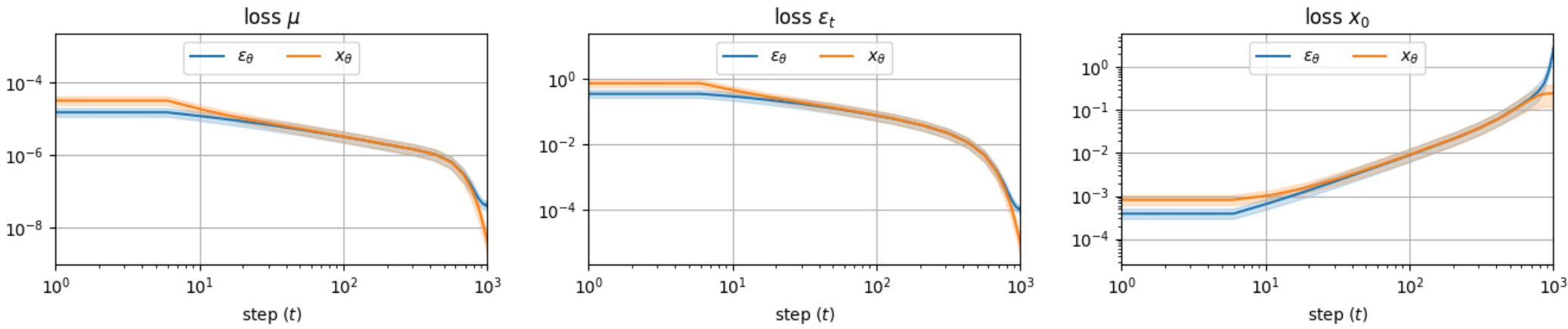
큰 $t$에서 $\epsilon_\theta$를 사용할 때의 loss가 $x_\theta$를 바로 사용할 때의 loss보다 상당히 크다.
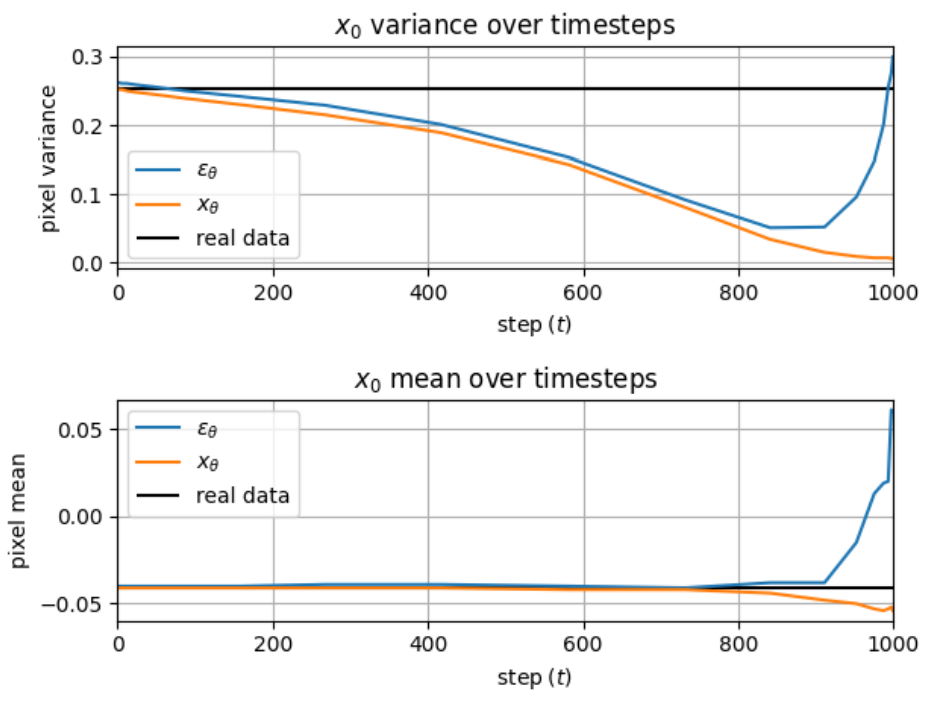
위 그래프는 예측된 $x_0$의 평균과 분산이 denoising process를 진행하면서 어떻게 달라지는 지를 나타낸 것이다. $\epsilon_\theta$를 사용하여 예측한 $x_0$는 굉장히 큰 편향과 분산으로 시작하여 여러 step으로 이를 수정한다. 반대로 $x_\theta$를 바로 사용한 예측은 즉시 낮은 편향에서 시작하며, 분산은 실제 데이터의 분산에 따라 단조 증가한다.
2. Pros and cons for predicting $x_0$
$x_0$를 바로 예측하는 것의 장점이자 단점은 모델이 그냥 입력에서 noise를 빼는 것이 아니라 전체 이미지를 생성해야 한다는 것이다. 이는 이미지가 매우 noisy한 초기 단계에서는 장점으로 작용한다. 위 그래프에서 볼 수 있듯이 편향되지 않은 이미지의 예측이 더 쉬우며 loss도 $\epsilon_\theta$보다 충분히 낮다. 반면 상당한 구조가 구성된 후반으로 가면 단점으로 작용한다. 단순히 작은 noise를 빼는 것이 아니라 $x_0$의 예측을 각 step마다 다시 해야한다. 작은 $t$에서 $x_\theta$를 사용하면 예측이 덜 정확해진다.
언뜻 보기에 $x_\theta$를 사용하는 backward process는 이미지 $x_0$가 $x_t$에서 빼지 않고 직접 추정되기 때문에 $\theta$의 residual 속성을 잃는 것처럼 보인다. 그러나 step $t$의 목적은 $x_0$을 예측하는 것이 아니라 \(\tilde{\mu}_t\)를 얻는 것이다. Residual 속성은 여전히 존재하며 $x_\theta$에 의존한다.
$\mu$를 계산할 때 $\epsilon_\theta$는 $x_t$에서 빼지지만 $x_\theta$는$ x_t$에 더해진다. 따라서 두 프로세스를 구분하기 위해 $\epsilon_\theta$ process는 “subtractive” backward process라 부르고 $x_\theta$ process는 “additive” backward process라 부른다.
Method
두 프로세스 모두의 장점을 활용하기 위해서 저자들은 $\epsilon_\phi$를 예측하는 $f_\phi (x_t, t)$와 $x_\psi$를 예측하는 $f_\psi (x_t, t)$를 고려하였다. 각 모델은 각자의 $\tilde{\mu}_t$를 추정하며, 얼마나 각 모델의 출력에 의존할 지를 조절하기 위해야 추가 parameter $r_t$를 사용하여 interpolate한다. 각 step $t$에서 서로 다른 $r_t$ 값을 선택하여 각 step에 각 프로세스가 얼마나 영향을 줄 지 조절할 수 있다.
이 방법을 간단하게 만들기 위해 $f_\phi$와 $f_\psi$를 하나의 모델 $f_\theta$로 융합하며, $r_t$도 같이 학습한다.
\[\begin{equation} \epsilon_\theta, x_\theta, r_\theta = f_\theta (x_t, t) \\ \mu_\theta = r_\theta \cdot \mu_x (x_\theta) + (1-r_\theta) \cdot \mu_\epsilon (\epsilon_\theta) \end{equation}\]아래 그림은 위 방법을 간단히 묘사한다.

모델의 유일한 변경점은 마지막 layer의 출력 채널이다. 예를 들어, $x_0, \epsilon \in \mathbb{R}^{H,W,C}$이고 $r \in \mathbb{R}^{H,W,1}$이면 $f_\theta$의 출력은 $\mathbb{R}^{H,W,C}$에서 $\mathbb{R}^{H,W,2C+1}$로 바뀐다. 이는 추가되는 파라미터의 수가 무시할 수 있는 수준임을 의미한다. $\mu_\theta$의 계산이 무시할 수 있는 수준이기 때문에 복잡도와 실행 시간도도 영향을 받지 않는다.
이 새로운 모델은 $\epsilon_\theta$, $x_\theta$, $r_\theta$를 최적화하는 새로운 손실 함수 $L_t$를 필요로 한다. 저자들은 손실 함수를 세 부분으로 나누었다.
\[\begin{equation} L_t^\epsilon = \| \epsilon - \epsilon_\theta \|^2 \\ L_t^x = \| x_0 - x_\theta \|^2 \\ L_t^\mu = \| \tilde{\mu}_t - (r_\theta [\mu_x (x_\theta)]_\textrm{sg} + (1-r_\theta) [\mu_\epsilon (\epsilon_\theta)]_\textrm{sg}) \|^2 \\ L_t = \lambda_t^\epsilon L_t^\epsilon + \lambda_t^x L_t^x + \lambda_t^\mu L_t^\mu \end{equation}\]\([\cdot]_\textrm{sg}\)는 “stop-grad”를 의미하며, 안의 값이 detach되어 기울기가 전파되지 않는다. $\lambda$들은 각 loss의 가중치이며 실험에서 모두 1로 유지된다. Stop gradient를 사용하지 않을 때보다 사용할 때 학습이 더 안정적이며, 이는 $\frac{\partial \mu_x}{\partial x_\theta}$와 $\frac{\partial \mu_\epsilon}{\partial \epsilon_\theta}$이 강하게 rescaling되기 때문이다.
1. Implicit sampling
DDIM은 $x_T$를 샘플링한 후 deterministic하게 생성이 진행된다. 본 논문의 방법은 $\mu_\theta$를 추정하는 것만 바뀌었기 때문에 DDIM의 implicit sampling을 수행하는 데에 아무런 영향이 없다.
\[\begin{equation} q(x_t \vert x_{t-1}, x_0) := \mathcal{N} (\mu_I, \sigma_t^2 I) \\ \mu_I := \sqrt{\vphantom{1} \bar{\alpha}_{t-1}} x_0 + \sqrt{1 - \bar{\alpha}_{t-1} - \sigma_t^2} \cdot \epsilon_t \end{equation}\]DDIM 논문에서는 $x_0$와 $\epsilon_t$가 \(\hat{x}_0 = x_0 (\epsilon_\theta)\)와 \(\hat{\epsilon}_t = \epsilon_\theta\)로 추정되었다. 본 논문에서는 다음 두 $\mu_I$의 추정을 interpolate하여 사용한다.
\[\begin{equation} \mu_{Ix} = \sqrt{\vphantom{1} \bar{\alpha}_t} x_\theta + \sqrt{1 - \bar{\alpha}_{t-1} - \sigma_t^2} \cdot \underbrace{\frac{x_t - \sqrt{\vphantom{1} \bar{\alpha}_t} x_\theta}{\sqrt{1 - \bar{\alpha}_t}}}_{\hat{\epsilon}_t} \\ \mu_{I \epsilon} = \underbrace{\frac{x_t - \sqrt{1 - \bar{\alpha}_t} \epsilon_\theta}{\sqrt{\alpha_t}}}_{\sqrt{\vphantom{1} \bar{\alpha}_{t-1}} \hat{x}_0} + \sqrt{1 - \bar{\alpha}_{t-1} - \sigma_t^2} \cdot \epsilon_\theta \end{equation}\]$\sigma_t = 0$이면 deterministic behavior가 얻어지며 모델은 확률적 접근법의 $\sigma_t^2$ 값에 민감하지 않다. DDIM의 또 다른 장점은 DDPM의 확률적 샘플링보다 훨씬 적은 iteration으로 예외적으로 잘 생성할 수 있다는 것이다. 이러한 이유들 때문에 본 논문의 실험은 대부분 이 방법을 따른다.
Experiments
1. Dual-Output Denoising
다음은 $\epsilon_\theta$로 예측하는 것(위)과 $x_\theta$로 예측하는 것(중간)이 얼마나 프로세스에 영향을 미치는 지 나타낸 것이다.

두 출력은 서로 다른 프로세스를 생성하며 어느정도 반대 역할을 한다. $\epsilon_\theta$를 사용하는 denoising process는 굉장히 noisy하게 시작하여 점진적으로 이전 추정값에서 noise가 제거된다. 반대로, $x_\theta$를 사용하는 denoising process는 여러 이미지의 평균과 유사한 굉장히 흐린 이미지에서 시작하여 반복적으로 컨텐츠가 추가된다. 이 서로 다른 시퀀스는 필연적으로 서로 다른 최종 이미지를 생성하지만, $x_T$는 이미지 space에서 두 이미지를 비슷한 방향으로 guide하기에 충분히 강한 조건인 것으로 보인다.
위 그림의 맨 아래 줄은 denoising process의 dual-output을 시각화한 것이다. 각 step의 interpolation 크기는 데이터셋에 따라 다르다. 예를 들어 CIFAR10의 dual-output process는 $x_\theta$와 매우 유사하게 시작하지만 CelebA의 경우 혼합되어 있다. Dual-output 결과도 두 데이터셋에 대하여 다르다. CIFAR10의 경우 dual-output이 $\epsilon_\theta$보다 noise가 적은 이미지를 생성하고 $x_\theta$보다 더 선명한 이미지를 생성하는 것을 관찰할 수 있다. CelebA의 경우 dual-output의 이미지 품질이 더 높다. 예를 들어 머리카락이 더 세련되고 안경이 눈에 띈다.
각 출력의 denoising process를 더 잘 이해하기 위하여 저자들은 subtractive와 additive를 중간에 바꾸는 추가 실험을 진행하였다. 다음 그림은 $x_\theta$에서 시작한 모델이 어떤 지점에서 $\epsilon_\theta$로 task를 이어나갈 때의 결과를 보여준다.
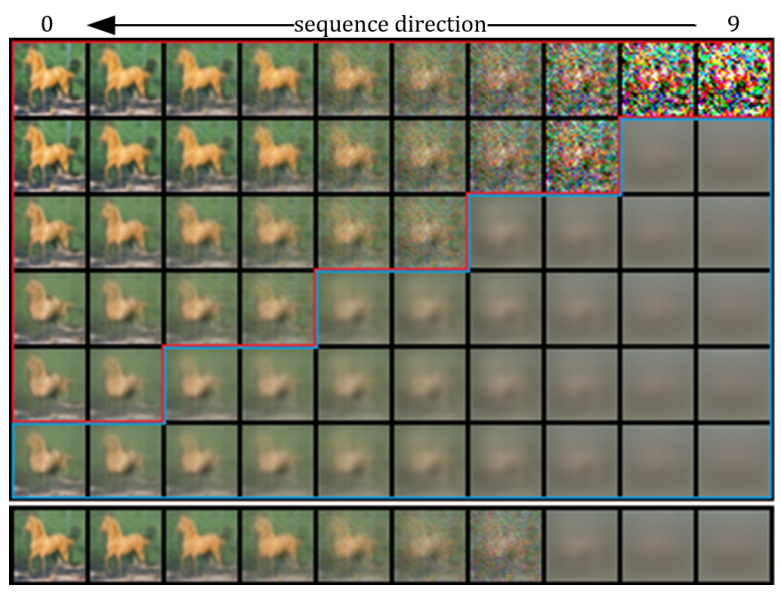
빨간색 테두리로 표시한 부분이 $\epsilon_\theta$를 사용한 것이고, 파란색 테두리로 표시한 부분이 $x_\theta$를 사용한 것이다. 맨 아래 줄은 dual-output을 나타낸다.
$x_\theta$를 사용한 생성은 만족스러운 이미지를 생성하지 못했으며 $\epsilon_\theta$를 사용한 생성이 우수했다. 그러나 두 가지를 혼합하면 최상의 결과를 얻을 수 있는 것처럼 보인다. 이것은 모델이 어떻게 진행할지 동적으로 선택할 수 있도록 하는 적응형 interpolation을 사용한 이유이다.
각 step $t$에 대한 상수 $r_t$를 학습하는 것보다 동적 interpolation parameter를 사용하는 것이 얼마나 더 나은지 질문할 수 있다. 이를 답하기 위하여 저자들은 여러 denoising process에 대한 각 step의 $r_\theta$를 측정하였다.
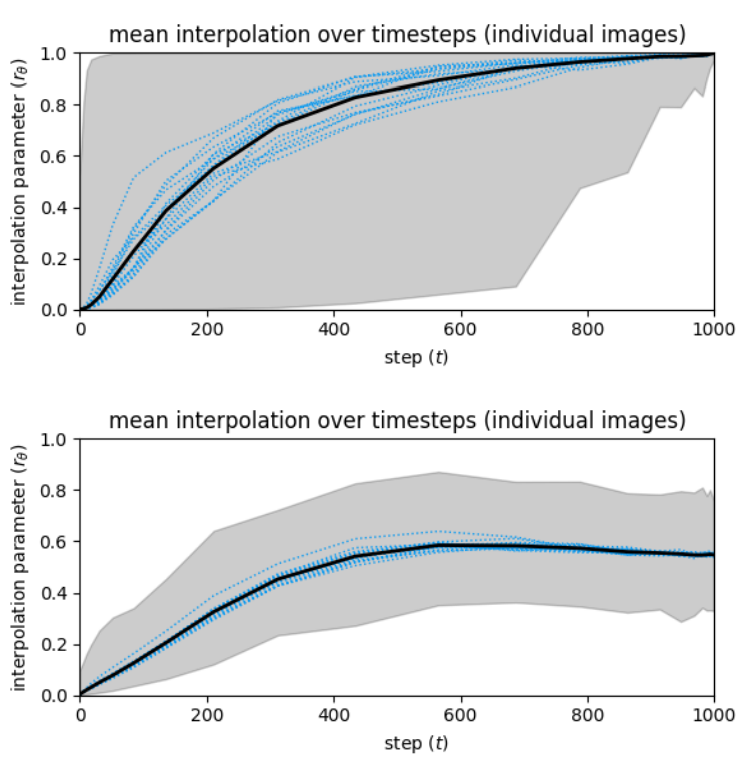
위 그래프는 각 step $t$에 대한 $r_\theta$를 나타낸 것이다. 위의 그래프는 CIFAR10에 대한 그래프고 아래 그래프는 CelebA에 대한 그래프다. $r_\theta$의 평균값은 검은색으로 나타냈고 회색 영역은 파라미터의 동적 범위를 나타낸다. 또한 16개의 궤적의 $r_\theta$의 평균값을 파란색으로 나타냈다.
이 시각화는 $r_\theta$가 취하는 궤적에 큰 가변성이 있음을 보여준다. 또한, 특정 생성 프로세스와 관련하여 일반적으로 전체 평균이 아닌 다른 값을 선호하는 것을 볼 수 있다.
놀랍게도 $r_\theta$가 데이터셋마다 다른 양상을 보인다는 것을 알 수 있다. CIFAR10의 경우 interpolation이 명확하다. 처음에는 $x_\theta$를 향한 매우 높은 선호도를 보이다가 중간부터 $\epsilon_\theta$를 향해 빠르게 떨어진다. CelebA의 경우 $r_\theta$가 0.5 정도에서 시작하고 상대적으로 좁은 범위를 유지하다가 마찬가지로 후반부에 $\epsilon_\theta$를 향해 빠르게 떨어진다. 두 데이터셋 모두 subtractive process에 대한 매우 높은 선호도로 denoising process가 종료된다.
2. Image Quality
다음은 CIFAR10과 CelebA에서 FID를 평가한 표이다.
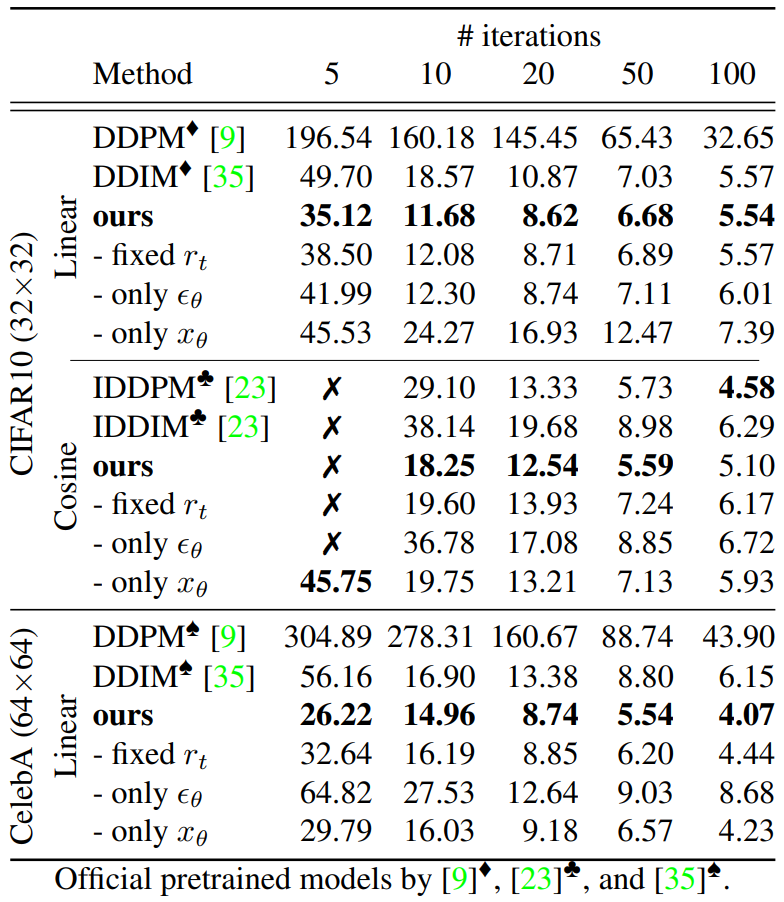
다음은 CIFAR10에서 생성한 이미지이다. (a)는 5 step, (b)는 10 step, (c)는 20 step으로 생성하였고, 위는 DDIM, 아래는 본 논문의 방법을 사용한 것이다.

다음은 ImageNet에서 생성한 이미지다. 모두 같은 $x_T$에서 생성을 시작하였다.

다음은 ImageNet 128$\times$128에서의 생성을 평가한 표이다.
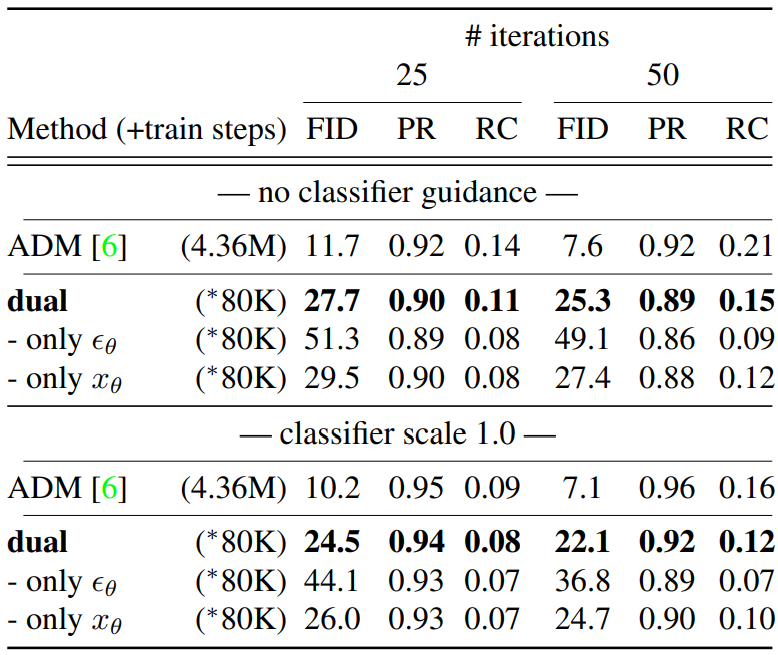
ImageNet의 경우 baseline인 ADM이 high-end device에서 436만 iteration으로 학습되었기 때문에 비교에 알맞지는 않다. 대신에 저자들은 사전 학습된 ADM의 인코더 부분의 가중치를 그대로 사용하고 디코더와 residual block만 8만 iteration으로 학습하였다고 한다.
Limitations
$L_t^\mu$ 식에서 파생된 next-step 측정값을 고려하여 $r_\theta$에 대한 유효 값을 선택할 수 있지만 이것이 생성 프로세스의 끝에서 반드시 최적의 이미지 품질로 이어지는 것은 아니다. 이러한 greedy 방식이 최적에 가깝다고 직관적으로 예상할 수 있지만 이를 위해서는 검증이 필요하다. 언어 생성 모델과 비슷하게 greedy 방식보다 beam search 방식이 이미지 품질을 더 향상시킬 수 있다.