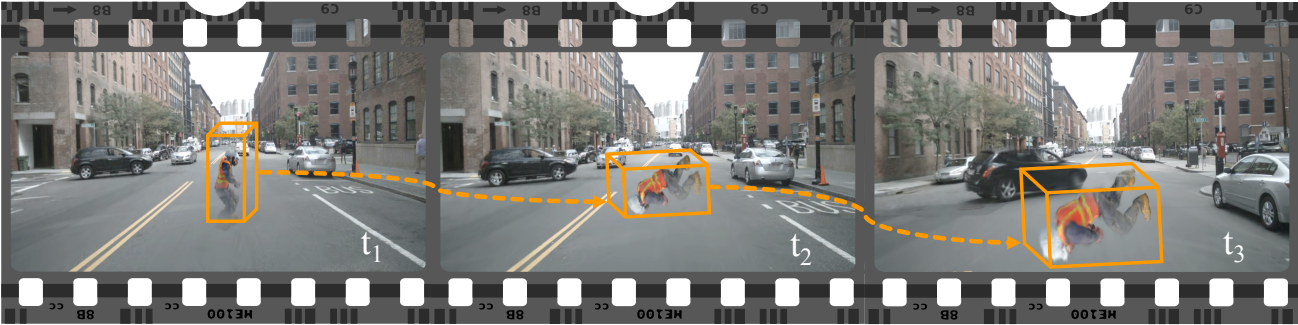
[논문리뷰] DrivingGaussian: Composite Gaussian Splatting for Surrounding Dynamic Autonomous Driving Scenes

CVPR 2024. [Paper] [Page]
Xiaoyu Zhou, Zhiwei Lin, Xiaojun Shan, Yongtao Wang, Deqing Sun, Ming-Hsuan Yang
Peking University | Google Research | University of California
13 Dec 2023

1. Introduction

차량에 장착된 sparse한 센서 데이터에서 복잡한 3D 장면을 재구성하는 것은 어려운 일이며, 특히 차량이 고속으로 이동할 때 더욱 그렇다. 왼쪽 전면 카메라가 포착한 장면의 가장자리에 차량이 나타나 전면 카메라 시야의 중앙으로 빠르게 이동하고, 다음 프레임에서 먼 점으로 줄어드는 장면을 상상해보자. 이러한 운전 장면의 경우 차량과 동적 객체가 모두 상대적으로 빠른 속도로 움직이므로 장면 구성에 심각한 문제가 발생한다. 정적인 배경과 동적인 사물은 제한된 시야를 통해 빠르게 변화하며 표현된다. 또한 다중 카메라 세팅에서는 외부 뷰, 최소한의 겹침, 다양한 방향에서 나오는 빛의 변화로 인해 훨씬 더 어려워진다. 복잡한 형상, 다양한 광학적 저하, 시공간적 불일치 역시 이러한 360도 대규모 운전 장면을 모델링하는 데 중요한 과제를 제기한다.

3D Gaussian Splatting(3D-GS)는 보다 명확한 3D Gaussian 표현으로 장면을 표현하고 새로운 뷰 합성에서 인상적인 성능을 달성하였다. 그러나 원래의 3D-GS는 고정된 Gaussian과 제한된 표현 용량으로 인해 대규모 동적 운전 장면을 모델링하는 데 여전히 심각한 문제에 직면해 있다. 각 타임스탬프에서 Gaussian을 구성하여 3D-GS를 동적 장면으로 확장하려는 노력이 있었다. 불행하게도 그들은 개별 동적 객체에 초점을 맞추고 정적-동적 영역이 결합되어 있고 고속으로 움직이는 여러 객체가 포함된 복잡한 주행 장면을 처리하지 못하였다.

본 논문에서는 동적인 자율주행 장면을 표현하는 새로운 프레임워크인 DrivingGaussian을 소개한다. 핵심 아이디어는 여러 센서의 순차적 데이터를 사용하여 복잡한 운전 장면을 계층적으로 모델링하는 것이다. 저자들은 Composite Gaussian Splatting을 채택하여 전체 장면을 정적 배경과 동적 객체로 분해하고 각 부분을 별도로 재구성하였다. 특히, 먼저 Incremental Static 3D Gaussian을 사용하여 다중 카메라 뷰로부터 포괄적인 장면을 순차적으로 구성한다. 그런 다음 Composite Dynamic Gaussian Graph를 사용하여 움직이는 각 객체를 개별적으로 재구성하고 Gaussian graph를 기반으로 정적 배경에 동적으로 통합한다. 이를 기반으로 Gaussian Splatting을 통한 글로벌 렌더링은 정적 배경과 동적 객체를 포함하여 현실 세계의 occlusion 관계를 캡처한다. 또한 랜덤 초기화나 SfM에 의해 생성된 포인트 클라우드를 활용하는 것보다 더 정확한 형상을 복구하고 더 나은 멀티뷰 일관성을 유지할 수 있는 GS 표현에 LiDAR prior를 통합하였다.

본 논문의 방법은 공공 자율주행 데이터셋에서 SOTA 성능을 달성하였다. LiDAR prior가 없더라도 본 논문의 방법은 여전히 유망한 성능을 제공하여 대규모 동적 장면을 재구성하는 데 있어 다양성을 보여준다. 또한 동적 장면 구성과 코너 케이스 시뮬레이션을 가능하게 하여 자율주행 시스템의 안전성과 견고성을 쉽게 검증할 수 있다.

Method

1. Composite Gaussian Splatting

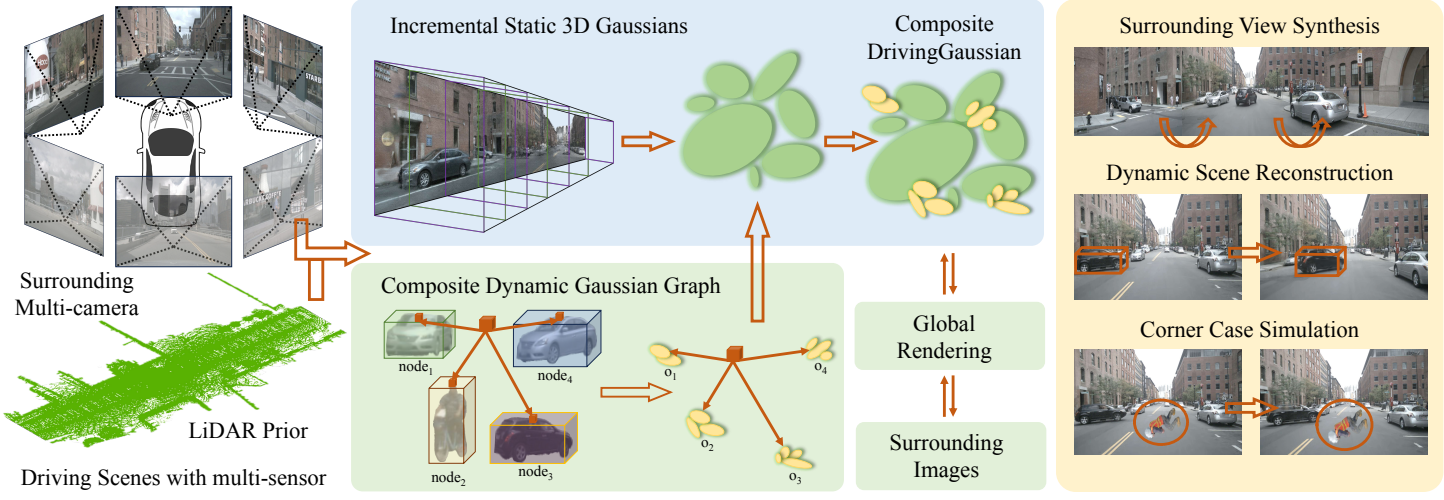
3D-GS는 순수한 정적 장면에서는 잘 작동하지만 대규모 정적 배경과 여러 동적 객체가 포함된 혼합 장면에서는 상당한 제한이 있다. 위 그림에서 볼 수 있듯이, 본 논문은 무한한 정적 배경과 동적 객체에 대해 Composite Gaussian Splatting을 사용하여 주변의 대규모 운전 장면을 표현하는 것을 목표로 하였다.

Incremental Static 3D Gaussians

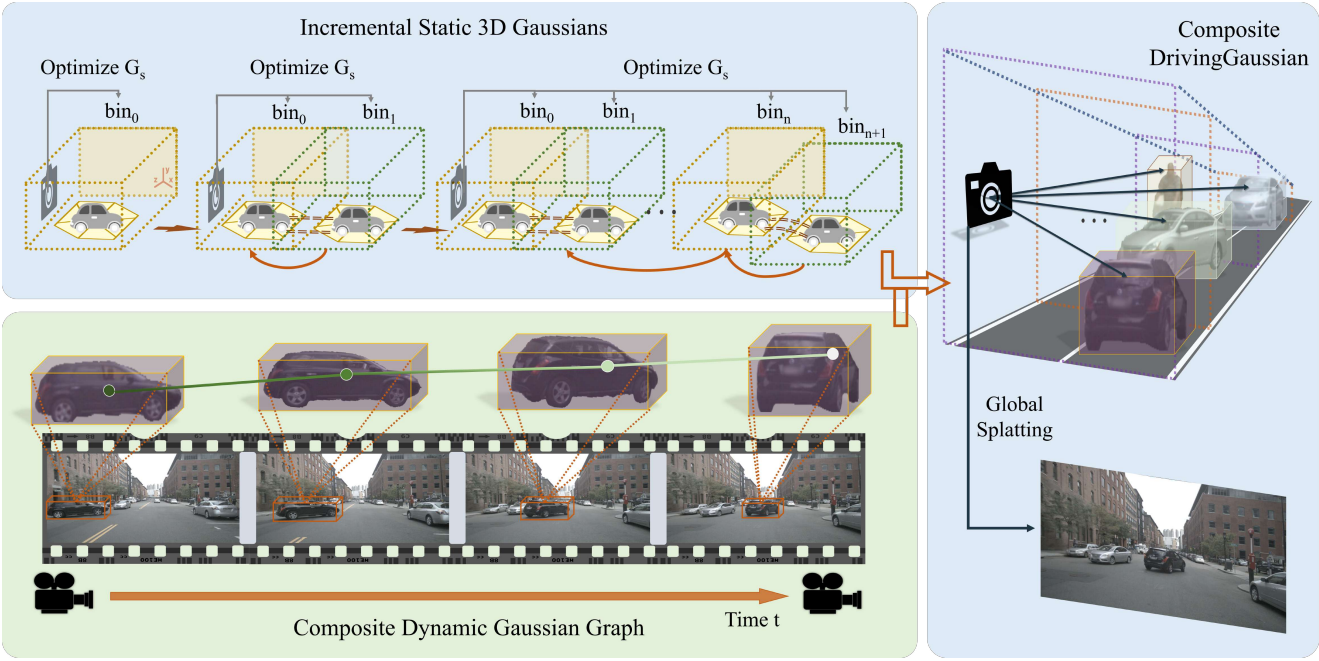
운전 장면의 정적인 배경은 대규모, 장기간, 다중 카메라 변환을 통한 차량 움직임의 변화로 인해 어려움을 겪는다. 차량이 움직일 때 정적 배경은 빈번하게 시간적 이동과 변화를 겪는다. 원근법에 인해 현재에서 멀리 떨어진 timestep에서 먼 거리의 장면을 성급하게 통합하면 스케일 혼란이 발생하여 아티팩트와 흐릿함이 발생할 수 있다. 이 문제를 해결하기 위해 저자들은 위 그림과 같이 차량의 움직임으로 인한 관점 변화와 인접 프레임 간의 시간적 관계를 활용하여 Incremental Static 3D Gaussian을 도입하여 3D-GS를 향상시킨다.

구체적으로 먼저 LiDAR prior에서 제공한 깊이 범위를 기반으로 정적 장면을 $N$개의 bin으로 균일하게 나눈다. 이러한 bin들 \(\{b_i\}^N\)은 시간순으로 정렬된다. 여기서 각 bin에는 하나 이상의 timestep의 다중 카메라 이미지가 포함된다. 첫 번째 bin 내의 장면에 대해 LiDAR prior를 사용하여 Gaussian 모델을 초기화한다.

\[\begin{equation} p_{b_0} (l \vert \mu, \Sigma) = \exp (-\frac{1}{2} (l - \mu)^\top \Sigma^{-1} (l - \mu)) \end{equation}\]

여기서 $l \in \mathbb{R}^3$은 LiDAR prior의 위치, $\mu$는 LiDAR 포인트의 평균, $\Sigma \in \mathbb{R}^{3 \times 3}$은 공분산 행렬이다. Gaussian 모델의 파라미터를 업데이트하기 위해 이 bin segment 내의 주변 뷰를 supervision으로 활용한다.

이후의 bin들의 경우 이전 bin의 Gaussian을 위치 prior로 사용하고 겹치는 영역을 기준으로 인접한 bin을 정렬한다. 각 bin의 3D 중심은 다음과 같이 정의할 수 있다.

\[\begin{equation} \hat{P}_{b+1} (G_s) = P_b (G_s) \cup (x_{b+1}, y_{b+1}, z_{b+1}) \end{equation}\]

여기서 $\hat{P}$는 현재 보이는 모든 영역의 Gaussian $G_s$에 대한 3D 중심 모음이고, $(x_{b+1}, y_{b+1}, z_{b+1})$은 $b+1$ 영역 내의 Gaussian 좌표이다. 반복적으로, supervision으로서 여러 주변 프레임을 사용하여 이전에 구성된 Gaussian에 나중 bin들의 장면을 통합한다. Incremental Static 3D Gaussian 모델 $G_s$는 다음과 같이 정의할 수 있다.

\[\begin{equation} \hat{C} (G_s) = \sum_{b=1}^N \Gamma_b \alpha_b C_b, \quad \Gamma_b = \prod_{i=1}^{b-1} (1 - \alpha_b) \end{equation}\]

여기서 $C$는 특정 뷰에서 각 단일 Gaussian에 해당하는 색상이고, $\alpha$는 불투명도, $\Gamma$는 모든 bin에서 $\alpha$에 따른 장면의 누적 투과율이다. 이 과정에서 주변 다중 카메라 이미지 간의 겹치는 영역을 사용하여 Gaussian 모델의 암시적 정렬을 공동으로 형성한다.

정적 Gaussian 모델을 증분적으로 구성하는 동안 전면 카메라와 후면 카메라 간에 동일한 장면을 샘플링하는 데 차이가 있을 수 있다. 이 문제를 해결하기 위해 가중치 평균을 사용하여 3D Gaussian 투영 중에 장면의 색상을 최대한 정확하게 재구성한다.

\[\begin{equation} \tilde{C} = \varsigma (G_s) \sum \omega (\hat{C} (G_s) \vert R, T) \end{equation}\]

여기서 $\tilde{C}$는 최적화된 픽셀 색상, $\varsigma$는 differential splatting, $\omega$는 다양한 뷰에 대한 가중치, $[R, T]$는 다중 카메라 뷰를 정렬하기 위한 뷰 행렬이다.

Composite Dynamic Gaussian Graph

자율주행 환경은 여러 개의 동적 객체와 시간적 변화를 포함하여 매우 복잡하다. 차량과 동적 객체의 움직임으로 인해 제한된 뷰(ex. 2~4개의 뷰)에서 객체가 관찰되는 경우가 많다. 또한 속도가 빠르면 동적 객체에 상당한 공간 변화가 발생하므로 고정된 Gaussian들을 사용하여 이를 표현하는 것이 어려워진다.

이러한 문제를 해결하기 위해 저자들은 대규모 장기 운전 장면에서 여러 개의 동적 객체를 구성할 수 있는 Composite Dynamic Gaussian Graph를 도입했다. 먼저 정적 배경에서 동적 전경 객체를 분해하여 데이터셋에서 제공하는 bounding box를 사용하여 동적 Gaussian graph를 만든다. 동적 객체는 object ID와 해당 외형의 타임스탬프로 식별된다. 또한 Segment Anything Model은 bounding box 범위를 기반으로 동적 객체를 픽셀 단위로 정확하게 추출하는 데 사용된다.

그런 다음 동적 Gaussian graph를 다음과 같이 구축한다.

\[\begin{equation} H = \langle O, G_d, M, P, A, T \rangle \end{equation}\]

여기서 각 노드는 인스턴스 객체 $o \in O$를 저장하고, $g_i \in G_d$는 해당 동적 Gaussian이고, $m_o \in M$은 각 객체에 대한 변환 행렬이다. $p_o (x_t, y_t, z_t) \in P$는 bounding box의 중심 좌표이고 $a_o = (\theta_t, \phi_t) \in A$는 timestep $t \in T$에서 bounding box의 방향이다. 여기서는 각 동적 객체에 대해 별도로 Gaussian들을 계산한다. 변환 행렬 $m_o$를 사용하여 대상 객체 $o$의 좌표계를 정적 배경이 있는 월드 좌표로 변환한다.

\[\begin{equation} m_o^{-1} = R_o^{-1} S_o^{-1} \end{equation}\]

여기서 $R_o^{−1}$와 $S_o^{−1}$는 각 객체에 해당하는 rotation 행렬과 translation 행렬이다.

동적 Gaussian graph의 모든 노드를 최적화한 후 Composite Gaussian Graph를 사용하여 동적 객체와 정적 배경을 결합한다. 각 노드의 Gaussian 분포는 bounding box 위치와 방향을 기준으로 시간순으로 정적 Gaussian field로 연결된다. 여러 동적 객체 사이에 occlusion이 있는 경우 카메라 중심으로부터의 거리를 기준으로 불투명도를 조정한다. 객체에 가까울수록 불투명도가 더 높다.

\[\begin{equation} \alpha_{o,t} = \sum \frac{(p_t - b_o)^2 \cdot \textrm{cot} \alpha_o}{\| (b_o \vert R_0, S_0) - \rho \|^2} \alpha_{p_0} \end{equation}\]

여기서 \(\alpha_{o,t}\)는 timestep $t$에서 객체 $o$에 대해 조정된 Gaussian의 불투명도이고, $p_t = (x_t, y_t, z_t)$는 객체에 대한 Gaussian의 중심이다. $[R_o, S_o]$는 object-to-world 변환 행렬, $\rho$는 카메라 뷰의 중심, \(\alpha_{p_0}\)는 Gaussian의 불투명도이다.

마지막으로 정적 배경과 여러 동적 객체를 모두 포함하는 composite Gaussian field는 다음과 같이 공식화될 수 있다.

\[\begin{equation} G_\textrm{comp} = \sum H \langle O, G_d, M, P, A, T \rangle + G_s \end{equation}\]

여기서 $G_s$는 Incremental Static 3D Gaussians를 통해 얻어지고 $H$는 최적화된 동적 Gaussian graph이다.

2. LiDAR Prior with surrounding views

3D-GS는 Structure-from-Motion (SfM)을 통해 Gaussian을 초기화한다. 그러나 자율주행을 위한 무한한 도시 장면에는 다양한 규모의 배경과 전경이 많이 포함되어 있다. 그럼에도 불구하고 그것들은 극히 sparse한 뷰를 통해서만 엿볼 수 있으며, 그 결과 기하학적 구조가 잘못되고 불완전하게 복원된다.

Gaussian에 대한 더 나은 초기화를 제공하기 위해 3D Gaussian에 LiDAR prior를 도입하여 더 나은 형상을 얻고 주변 뷰에서 다중 카메라 일관성을 유지한다. 각 timestep $t \in T$에서 다중 카메라 이미지 세트 \(\{I_t^i \vert i = 1 \ldots N\}\)가 움직이는 플랫폼과 다중 프레임 LiDAR sweep $L_t$에서 수집된다. LiDAR-이미지 멀티모달 데이터를 사용하여 다중 카메라 오차를 최소화하고 정확한 포인트 위치와 geometric prior를 얻는 것을 목표로 한다.

먼저 LiDAR sweep의 여러 프레임을 병합하여 장면의 완전한 포인트 클라우드 $L$을 얻는다. COLMAP으로 각 이미지에서 이미지 feature $X = x_p^q$를 개별적으로 추출한다. 다음으로 LiDAR 포인트를 주변 이미지에 투영한다. 각 LiDAR 포인트 $l$에 대해 해당 좌표를 카메라 좌표계로 변환하고 projection을 통해 카메라 이미지 평면의 2D 픽셀과 일치시킨다.

\[\begin{equation} x_p^q = K [R_t^i \cdot l_s + T_t^i] \end{equation}\]

여기서 $x_p^q$는 이미지 $I_t^i$의 2D 픽셀이고, $R_t^i$d와 $T_t^i$는 각각 orthogonal rotation matrix와 translation vector이다. $K \in \mathbb{R}^{3 \times 3}$은 알고 있는 camera intrinsic이다. 특히 LiDAR의 포인트는 여러 이미지의 여러 픽셀에 투영될 수 있다. 따라서 이미지 평면까지의 유클리드 거리가 가장 짧은 점을 선택하고 이를 투영된 점으로 유지하여 색상을 할당한다.

3D 재구성의 이전 연구들과 유사하게 dense bundle adjustment (DBA)을 다중 카메라 세팅으로 확장하고 업데이트된 LiDAR 포인트를 얻는다. 주변 다중 카메라와 정렬하기 전에 LiDAR로 초기화하면 Gaussian 모델에 보다 정확한 기하학적 형상을 제공하는 데 도움이 된다.

3. Global Rendering via Gaussian Splatting

미분 가능한 3D-GS 렌더러 $\varsigma$를 채택하고 글로벌 composite 3D Gaussian을 2D로 투영한다. 여기서 공분산 행렬 $\tilde{\Sigma}$는 다음과 같다.

\[\begin{equation} \tilde{\Sigma} = J E \Sigma E^\top J^\top \end{equation}\]

여기서 $J$는 perspective projection의 Jacobian 행렬이고 $E$는 world-to-camera matrix이다.

Composite Gaussian field는 글로벌 3D Gaussian을 여러 2D 평면에 투영하고 각 timestep에서 주변 뷰를 사용하여 supervise된다. 글로벌 렌더링 프로세스에서 다음 timestep의 Gaussian은 처음에는 현재에 보이지 않으며 이후 해당 글로벌 이미지의 supervision과 함께 통합된다.

Loss function은 세 부분으로 구성된다. 먼저 렌더링된 타일과 해당 ground-truth 간의 유사성을 측정하는 Tile Structural Similarity (TSSIM)을 Gaussian Splatting에 도입한다.

\[\begin{equation} L_\textrm{TSSIM} (\delta) = 1 - \frac{1}{Z} \sum_{z=1}^Z \textrm{SSIM} (\Psi (\hat{C}), \Psi (C)) \end{equation}\]

여기서 $M$은 분할한 타일의 수, $\delta$는 Gaussian의 학습 파라미터, $\Psi(\hat{C})$는 Composite Gaussian Splatting에서 렌더링된 타일, $\Psi(C)$는 쌍을 이루는 ground-truth 타일이다.

또한 3D Gaussian의 outlier를 줄이기 위한 다음과 같이 정의된 robust loss를 도입한다.

\[\begin{equation} L_\textrm{robust} (\delta) = \kappa (\| \hat{I} - I \|_2) \end{equation}\]

여기서 $\kappa \in (0, 1]$은 loss의 robustness를 제어하는 형상 파라미터이고, $I$와 $\hat{I}$는 각각 ground-truth 및 합성 이미지이다.

LiDAR loss는 LiDAR에서 예상되는 Gaussian 위치를 supervise하여 더 나은 기하학적 구조와 가장자리 모양을 얻기 위해 추가로 사용된다.

\[\begin{equation} L_\textrm{LiDAR} (\delta) = \frac{1}{s} \sum \| P (G_\textrm{comp}) - L_s \|^2 \end{equation}\]

여기서 \(P (G_\textrm{comp})\)는 3D Gaussian의 위치이고 $L_s$는 LiDAR prior의 포인트이다. 세 가지 loss의 합을 최소화하여 Composite Gaussian을 최적화한다.

Experiments

• 데이터셋: nuScenes, KITTI-360
• 구현 디테일
  • 계산 비용을 고려하여 LiDAR 포인트에 복셀 그리드 필터를 사용하여 기하학적 feature들을 잃지 않고 규모를 줄임
  • 대규모 장면에서 객체가 상대적으로 작다는 점을 고려하여 초기 포인트가 3000으로 설정된 동적 객체에 대해 무작위 초기화를 사용
  • iteration: 50,000
  • 밀도 증가 임계값을 0.001로 설정하고 불투명도 간격을 900으로 재설정
  • learning rate
    • Incremental Static 3D Gaussians: 3D-GS와 동일하게 유지
    • Composite Dynamic Gaussian Graph: $1.6 \times 10^{-3}$에서 $1.6 \times 10^{-6}$으로 exponentially decay
  • GPU: P40 8개 (총 192GB)

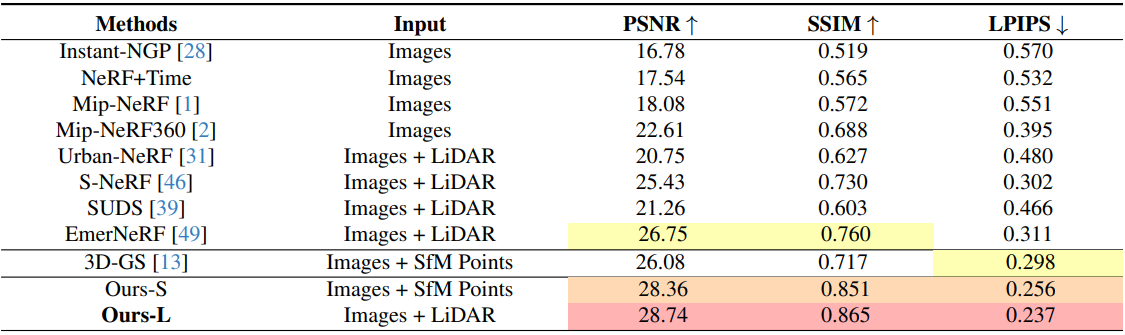
1. Results and Comparisons

다음은 nuScenes에서 기존 SOTA 방법들과 전체적인 성능을 비교한 표이다.

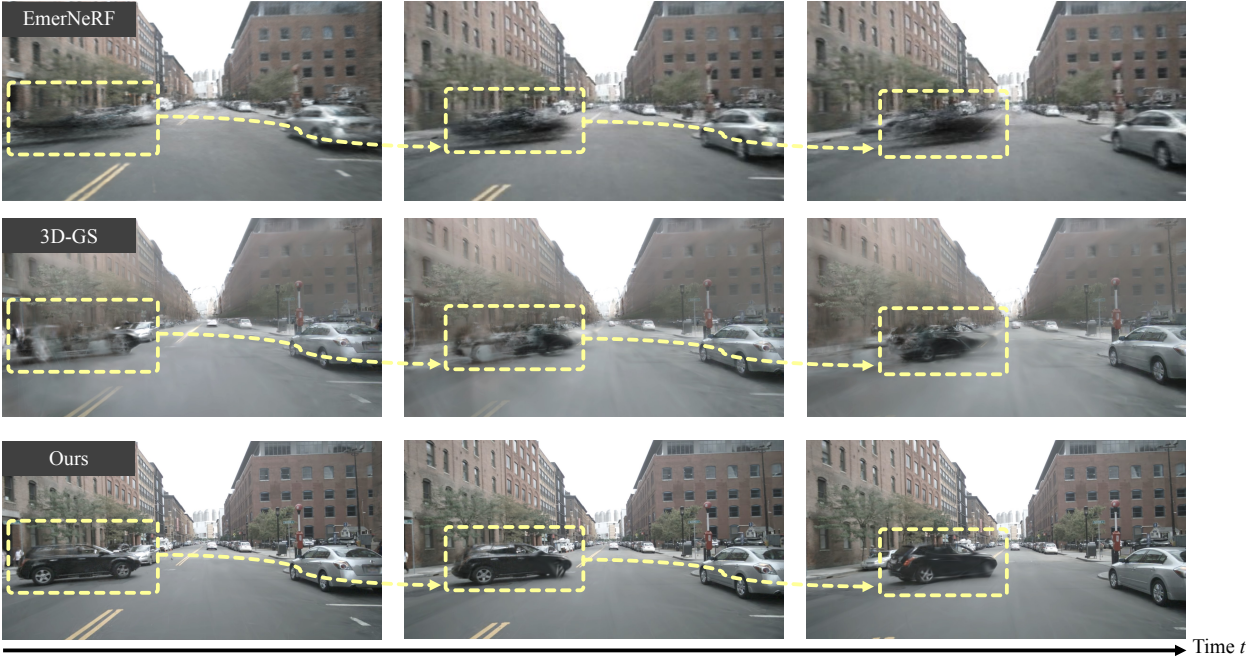
다음은 nuScenes에서 재구성 결과를 비교한 것이다.

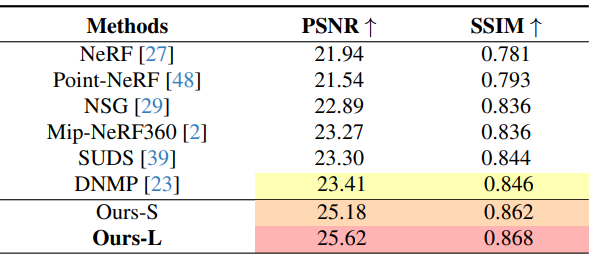
다음은 KITTI-360에서 기존 SOTA 방법들과 전체적인 성능을 비교한 표이다.

2. Ablation Study

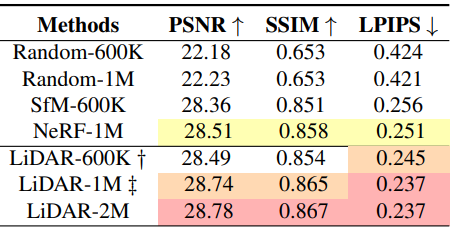
다음은 초기화 방법에 대한 ablation 결과이다.

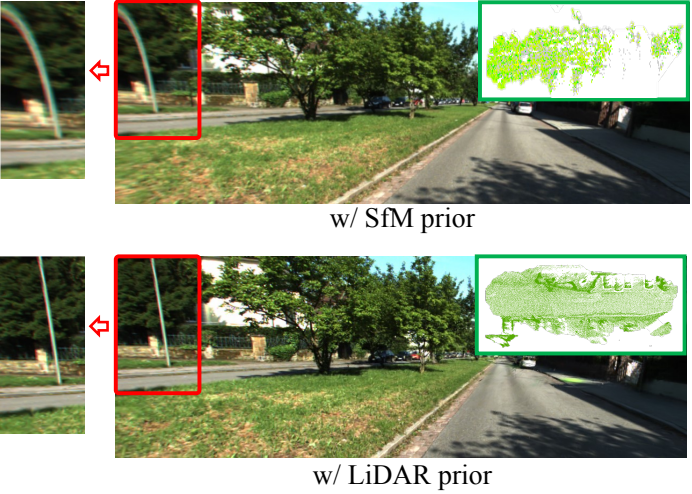
다음은 KITTI-360에서 초기화 방법에 따른 결과를 시각적으로 비교한 것이다.

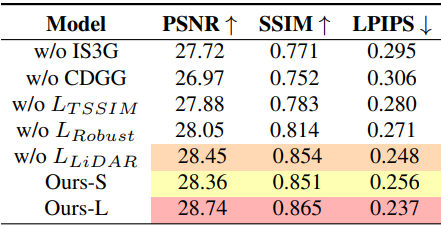
다음은 각 모듈에 대한 ablation 결과이다.

3. Corner Case Simulation

다음은 코너 케이스 시뮬레이션의 예시이다.