Diffusion은 신이고 GPT는 무적이다

arXiv 2023. [Paper] [Page] [Github]
Yujun Shi, Chuhui Xue, Jiachun Pan, Wenqing Zhang, Vincent Y. F. Tan, Song Bai
National University of Singapore | ByteDance Inc.
9 Jul 2023

Introduction

생성 모델을 사용한 이미지 편집은 최근 많은 관심을 받고 있다. 중요한 최근 연구 중 하나는 상호 작용하는 포인트 기반 이미지 편집, 즉 “드래그” 편집을 가능하게 하는 DragGAN이다. 이 프레임워크에서 사용자는 주어진 이미지에서 여러 쌍의 핸들 포인트와 타겟 포인트를 클릭한다. 그런 다음 모델은 핸들 포인트의 내용을 해당 타겟 포인트로 이동하는 의미론적으로 일관된 편집 결과를 이미지에 생성한다. 또한 사용자는 편집 가능한 이미지 영역을 지정하고 나머지 영역은 변경되지 않도록 지정하는 마스크를 그릴 수 있다. DragGAN은 인상적인 결과를 달성했지만 적용 가능성은 GAN 고유의 모델 용량에 의해 제한된다.

본 논문은 이를 해결하기 위해 diffusion model로 강화된 인터랙티브한 포인트 기반 이미지 편집 방법인 DragDiffusion을 제안한다. DragDiffusion을 사용하면 인터랙티브한 포인트 기반 편집 프레임워크를 위한 사전 학습된 대규모 diffusion model을 활용할 수 있으므로 드래그 편집의 일반성을 크게 향상시킬 수 있다. 대부분의 이전 diffusion 기반 이미지 편집 방법은 생성된 이미지를 편집하기 위해 주로 텍스트 임베딩 제어에 의존하기 때문에 정확한 픽셀 레벨의 공간 제어 대신 높은 레벨의 semantic 편집만 가능했다. 이러한 방법과 달리 DragDiffusion은 특정 step $t$에서 diffusion latent를 조작하여 출력 이미지를 편집한다. 이는 diffusion latent가 생성된 이미지의 공간 레이아웃을 결정할 수 있다는 관찰에서 영감을 얻었다.

인터랙티브한 포인트 기반 편집을 위해 motion supervision과 point tracking이라는 두 가지 연속되는 절차를 따르고 반복적으로 적용한다. 구체적으로, 먼저 타겟을 향해 이동하는 핸들 포인트를 supervise하는 motion supervision loss를 최소화하기 위해 $t$번째 step의 latent를 최적화한다. Motion supervision loss는 diffusion model의 UNet의 feature map을 사용하여 계산된다. Diffusion latent의 업데이트로 핸들 포인트의 위치도 변경될 수 있다. 따라서 핸들 포인트의 가장 최신 위치를 추적하기 위해 motion supervision 후에 point tracking 연산이 이어진다.

Diffusion model은 이미지를 생성하기 위해 여러 단계의 프로세스를 필요로 하기 때문에 DragDiffusion의 한 가지 잠재적인 우려는 $t$번째 step의 latent에서만 motion supervision과 point tracking을 적용하여 출력 이미지를 정확하게 조작할 수 있는지 여부이다. 저자들은 실험에서 $t$번째 step의 latent의 UNet feature map을 사용하면 정밀한 공간 조작을 수행하기에 충분하다는 것을 보였다. 이렇게 단순화된 디자인으로 DragDiffusion은 합리적인 시간에 편집 피드백을 제공할 수 있다.

그러나 위의 절차를 직접 적용할 때 발생할 수 있는 한 가지 문제는 편집 결과가 원하지 않는 객체 identity 또는 이미지 스타일의 이동으로 인해 어려움을 겪을 수 있다는 것이다. 예를 들어, 고양이 머리를 드래그하면 고양이 머리가 결국 개 머리로 변할 수 있다. 이미지를 편집할 때 스타일이 다른 스타일로 변경될 수 있다. 흥미롭게도 편집하기 전에 입력 이미지를 재구성하기 위해 UNet의 파라미터에서 LoRA를 fine-tuning하면 이 문제를 완화할 수 있다.

본 논문은 다양한 예제에 대한 광범위한 실험을 통해 DragDiffusion이 여러 개체, 다양한 개체 카테고리, 다양한 스타일과 같은 까다로운 사례에 적용 가능하며 인터랙티브한 포인트 기반 편집 프레임워크의 다양성과 일반성을 크게 향상시킨다는 것을 보여준다.

Methodology

1. Preliminaries on Diffusion Models

DDPM은 확률 밀도 $q(Z_0)$를 $Z_0$와 latent 변수들 $Z_{1:T}$ 사이의 결합 분포로 모델링한다.

\[\begin{equation} p_{Z_0} (z_0) = \int p_{Z_{0:T}} (z_{0:T}) dz_{1:T} \end{equation}\]

Latent 변수의 시퀀스 \((Z_T, Z_{T -1}, \cdots, Z_1, Z_0)\)는 표준 정규 분포 \(Z_T \sim \mathcal{N} (0, I)\)에서 시작하여 학습된 transition을 갖는 Markov chain을 형성한다. 본 논문에서 $Z_0$은 사용자가 제공한 이미지 샘플에 해당하고 $Z_t$는 diffusion process의 $t$ step 후 noisy한 이미지에 해당한다.

2. Method Overview

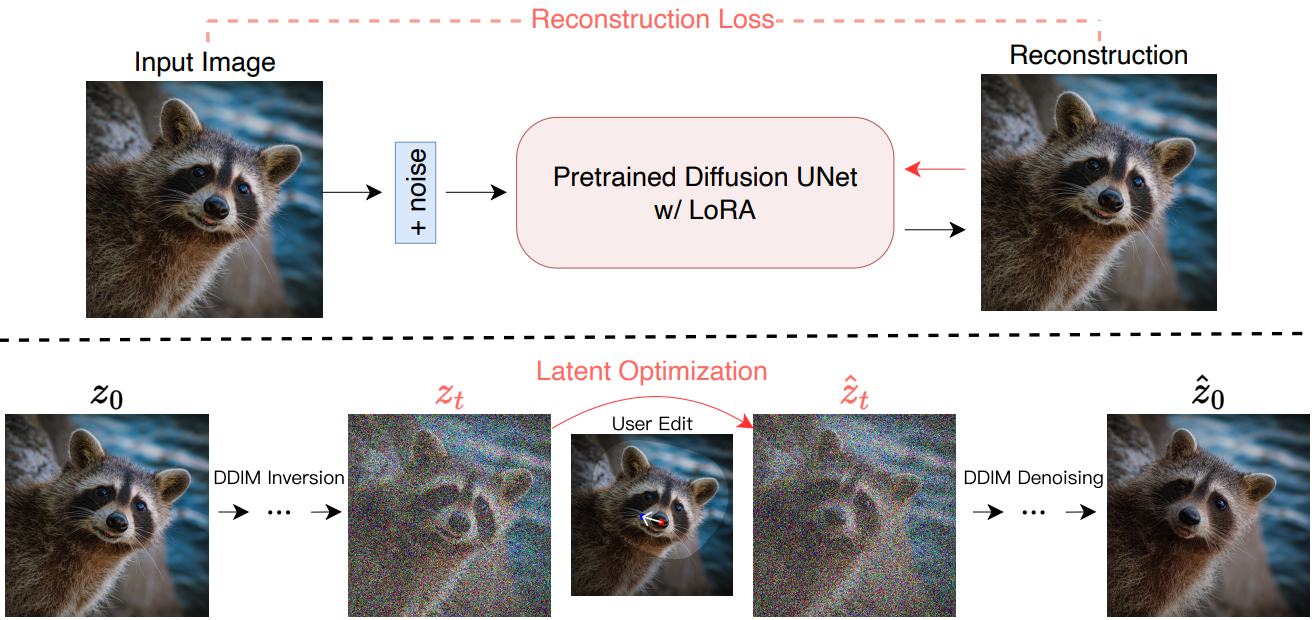
DragDiffusion은 인터랙티브한 포인트 기반 이미지 편집을 달성하기 위해 특정 diffusion latent를 최적화하는 것을 목표로 한다. 이 목표를 달성하기 위해 먼저 diffusion model에서 LoRA를 fine-tuning하여 사용자가 입력한 이미지를 재구성한다. 이러한 방식으로 편집 과정에서 개체의 identity와 입력 이미지의 스타일을 더 잘 보존할 수 있다. 다음으로 입력 이미지에 DDIM inversion을 적용하여 특정 step $t$의 diffusion latent를 얻는다. 그런 다음 motion supervision과 point tracking을 반복적으로 적용하여 이전에 획득한 $t$-step diffusion latent를 최적화하여 핸들 포인트의 콘텐츠를 타겟으로 끌어당긴다. 편집 프로세스 중에 이미지의 마스킹되지 않은 영역이 변경되지 않도록 정규화 항이 적용된다. 마지막으로 최적화된 $t$번째 step의 latent를 DDIM으로 denoise하여 사후 편집 결과를 얻는다. DragDiffusion의 개요는 아래 그림과 같다.

3. Motion Supervision and Point Tracking

Motion supervision

$k$번째 motion supervision iteration에서 $n$개의 핸들 포인트와 대응되는 타겟 포인트는 각각

\[\begin{equation} \{h_i^k = (x_i^k, y_i^k): i = 1, \cdots, n\}, \\ \{g_i = (\tilde{x}_i, \tilde{y}_i): i = 1, \cdots, n\} \end{equation}\]

로 표시된다. 입력 이미지는 $z_0$로 표시된다. $t$번째 step의 latent, 즉 $t$번째 step의 DDIM inversion의 결과는 $z_t$로 표시된다. 입력으로 $z_t$가 주어지면 끝에서 두 번째 UNet 블록의 feature map $F(z_t)$는 motion supervision을 수행하는 데 사용된다. 또한 픽셀 위치 $h_i^k = (x_i^k, y_i^k)$의 feature 벡터를 $F_{h_i^k} (z_t)$로 표시한다. 또한 $h_i^k$를 중심으로 한 변 길이가 $2r_1 + 1$인 정사각형 패치는

\[\begin{equation} \Omega (h_i^k, r_1) = \{(x, y): \vert x − x_i^k \vert \le r_1, \vert y − y_i^k \vert \le r_1\} \end{equation}\]

로 정의된다. 그런 다음 motion supervision의 $k$번째 iteration에 대해 최적화 문제의 목적 함수는 다음과 같이 정의된다.

\[\begin{aligned} \mathcal{L} (\hat{z}_t^k) = \;& \sum_{i=1}^n \sum_{q \in \Omega (h_i^k, r_1)} \| F_{q + d_i} (\hat{z}_t^k) - \textrm{sg} (F_q (\hat{z}_t^k)) \|_1 \\ & + \lambda \| (\hat{z}_{t-1}^k - \textrm{sg} (\hat{z}_{t-1}^0)) \odot (\unicode{x1D7D9} - M) \|_1 \\ d_i = \;& \frac{g_i - h_i^k}{\| g_i - h_i^k \|_2} \end{aligned}\]

여기서 \(\hat{z}_t^k\)는 $k$번째 motion supervision 후의 $t$번째 step의 latent이고 (\(\hat{z}_t^0 = z_t\)), $\textrm{sg}(\cdot)$는 stop gradient 연산자이다. $d_i$는 $i$번째 핸들 포인트에서 $i$번째 타겟 포인트로의 정규화된 방향이고, $M$은 사용자가 지정한 이진 마스크이다. \(F_{q+d_i} (\hat{z}_t^k)\)에서 $q+d_i$가 정수가 아닐 수 있으므로 bilinear interpolation을 통해 얻는다. 마스킹되지 않은 영역이 변경되지 않도록 권장하므로 UNet feature 대신 diffusion latent을 사용한다. 구체적으로 \(\hat{z}_t^k\) 가 주어지면 먼저 \(\hat{z}_{t-1}^k\)을 얻기 위해 DDIM denoising의 한 step을 적용한 다음 \(\hat{z}_{t-1}^k\)의 마스킹되지 않은 영역을 \(\hat{z}_{t-1}^0 = z_{t-1}\)과 동일하게 정규화한다. 마지막으로 \(\hat{z}_t^k\)는 각 motion supervision iteration에서 $\mathcal{L}$을 최소화하기 위해 하나의 gradient descent step을 수행하여 업데이트된다.

\[\begin{equation} \hat{z}_t^{k+1} = \hat{z}_t^k - \eta \cdot \frac{\partial \mathcal{L} (\hat{z}_t^k)}{\partial \hat{z}_t^k} \end{equation}\]

여기서 $\eta$는 learning rate이다.

Point Tracking

Motion supervision 업데이트가 \(\hat{z}_t^k\)를 변경하기 때문에 핸들 포인트의 위치도 변경될 수 있다. 따라서 diffusion latent를 최적화한 후 핸들 포인트를 업데이트하기 위해 point tracking을 수행해야 한다. \(F(\hat{z}_t^k)\)와 \(F(z_t)\)를 사용하여 새 핸들 포인트를 추적한다. 구체적으로, 다음과 같이 정사각형

\[\begin{equation} \Omega (h_i^k, r_2) = \{(x, y): \vert x − x_i^k \vert \le r_2, \vert y − y_i^k \vert \le r_2\} \end{equation}\]

내에서 nearest neighbor 검색으로 각 핸들 포인트 $h_i^k$를 업데이트한다.

\[\begin{equation} h_i^{k+1} = \underset{q \in \Omega (h_i^k, r_2)}{\arg \min} \| F_q (\hat{z}_t^{k+1}) - F_{h_i^k} (z_t) \|_1 \end{equation}\]

4. Implementation Details

  • Stable Diffusion 1.5을 diffusion model로 채택
  • LoRA fine-tuning
    • rank: 16
    • optimizer: AdamW
    • learning rate: $2 \times 10^{-4}$
    • 200 steps
  • 편집 단계
    • DDIM: 50 steps
    • 40번째 step의 latent를 최적화
    • optimizer: Adam
    • learning rate: 0.01
    • classifier-free guidance (CFG)는 수치적 오차를 증폭시키므로 사용하지 않음
    • $r_1$ = 1, $r_2$ = 3, $\lambda$ = 0.1

1. Qualitative Evaluation

다음은 주어진 이미지에 대하여 빨간색 핸들 포인트에서 파란색 타겟 포인트로 드래그한 편집 결과이다. 밝은 영역은 사용자가 지정한 편집 가능한 영역이다.


You may also enjoy