[논문리뷰] Direct Preference Optimization: Your Language Model is Secretly a Reward Model (DPO)
NeurIPS 2023 (Oral). [Paper]
Rafael Rafailov, Archit Sharma, Eric Mitchell, Stefano Ermon, Christopher D. Manning, Chelsea Finn
Stanford University | CZ Biohub
29 May 2023
Introduction
매우 큰 데이터셋에 대해 학습된 대규모 unsupervised 언어 모델(LM)은 놀라운 능력을 가지고 있다. 그러나 이러한 모델들은 다양한 목표, 우선 순위, 기술들을 사용하여 사람이 생성한 데이터를 기반으로 학습되었다. 이러한 목표와 기술 중 일부는 모방하는 것이 바람직하지 않을 수 있다. 예를 들어, AI 코딩 도우미가 일반적인 프로그래밍 실수를 이해하여 이를 수정하기를 원하지만 코드를 생성할 때 학습 데이터에 존재하는 고품질 코딩 능력 쪽으로 모델이 편향된다. 마찬가지로, 언어 모델이 50%의 사람들이 믿는 일반적인 오해를 인식하기를 원하지만 모델이 이 오해가 50%의 쿼리에서 사실이라고 주장하는 것을 원하지 않는다. 즉, 매우 폭넓은 지식과 능력에서 모델이 원하는 반응과 행동을 선택하는 것은 성능이 뛰어나며 안전하고 제어 가능한 AI 시스템을 구축하는 데 중요하다. 기존 방법들은 일반적으로 강화 학습(RL)을 사용하여 사람의 선호도와 일치하도록 LM을 조정하지만, 기존 방법에서 사용하는 RL 기반 목적 함수는 간단한 binary cross-entropy 목적 함수로 정확하게 최적화되어 선호도 학습 파이프라인을 크게 단순화할 수 있다.
기존 방법들은 사람이 안전하고 유용하다고 생각하는 행동 유형을 나타내는 선별된 선호도 세트를 사용하여 원하는 행동을 언어 모델에 주입하였다. 이 선호도 학습 단계는 대규모 텍스트 데이터셋에 대한 대규모 unsupervised 사전 학습의 초기 단계 후에 진행된다. 선호도 학습에 대한 가장 간단한 접근 방식은 인간의 고품질 응답에 대한 supervised fine-tuning인 반면, 가장 성공적인 방법은 사람(또는 AI)의 피드백을 통한 강화 학습이다. RLHF 방법은 reward model을 인간 선호도 데이터셋에 맞춘 다음 RL을 사용하여 언어 모델의 policy를 최적화하여 원래 모델에서 지나치게 벗어나지 않고 높은 reward가 할당된 응답을 생성한다. RLHF는 인상적인 대화 및 코딩 능력을 갖춘 모델을 생성하는 반면, 여러 LM을 학습시키고 LM policy의 샘플링 등 상당한 계산 비용이 발생하여 supervised learning보다 훨씬 더 복잡하다.
본 논문에서는 명시적인 reward 모델링이나 강화 학습 없이 사람의 선호도를 준수하도록 언어 모델을 직접 최적화하는 방법을 보여주었다. 저자들은 기존 RLHF 알고리즘(KL-divergence 제약 조건을 사용한 reward 최대화)과 동일한 목적 함수를 암시적으로 최적화하지만 구현이 간단하고 학습이 간편한 알고리즘인 Direct Preference Optimization (DPO)를 제안하였다.
DPO 업데이트는 선호되지 않는 응답에 대한 상대적인 log probability를 증가시키지만, 단순한 probability ratio 목적 함수에 의한 모델 저하를 방지하는 동적인 예제별 중요도 가중치를 통합하였다. 기존 알고리즘과 마찬가지로 DPO는 주어진 reward function이 경험적 선호도 데이터와 얼마나 잘 일치하는지 측정하는 이론적 선호도 모델(ex. Bradley-Terry model)에 의존한다. 그러나 기존 방법에서는 선호도 loss를 정의하여 reward model을 학습시킨 다음 학습된 reward model을 최적화하는 policy를 학습시키는 반면, DPO는 change-of-variables(변수 변환)을 사용하여 선호도 loss를 policy의 함수로 직접 정의한다. 따라서 모델 응답에 대한 인간 선호도 데이터셋이 주어지면 DPO는 reward function을 명시적으로 학습하거나 학습 중에 policy에서 샘플링하지 않고도 간단한 binary cross-entropy 목적 함수를 사용하여 policy를 최적화할 수 있다.
Preliminaries: RLHF
RLHF는 일반적으로 3단계로 구성된다.
1. Supervised fine-tuning (SFT) 단계
RLHF는 일반적으로 사전 학습된 LM에서 시작하여 관심 있는 다운스트림 task의 고품질 데이터셋에 대한 supervised learning으로 fine-tuning된 모델 $\pi^\textrm{SFT}$를 얻는다.
2. Reward 모델링 단계
두 번째 단계에서 SFT 모델은 프롬프트 $x$로 프롬프팅되어 답의 쌍 $(y1, y2) \sim \pi^\textrm{SFT} (y \vert x)$를 생성한다. 그런 다음 답 쌍이 인간 라벨러에게 제시되며 라벨러는 하나의 답변에 대한 선호도 $y_w \succ y_l \vert x$를 표현한다. 여기서 $y_w$와 $y_l$은 각각 $(y1, y2)$ 중에서 선호하는 답과 선호하지 않는 답을 나타낸다. 선호도는 접근할 수 없는 어떤 latent reward model $r^\ast (x, y)$에 의해 생성된 것으로 가정된다. 선호도를 모델링하는 데 사용되는 접근 방식에는 여러 가지가 있으며, Bradley-Terry (BT) 모델이 인기 있는 선택이다. BT 모델은 사림의 선호도 분포 $p^\ast$가 다음과 같다고 규정한다.
\[\begin{equation} p^\ast (y_1 \succ y_2 \vert x) = \frac{\exp (r^\ast (x, y_1))}{\exp (r^\ast (x, y_1)) + \exp (r^\ast (x, y_2))} \end{equation}\]$p^\ast$에서 샘플링된 비교 데이터셋 \(\mathcal{D} = \{x^{(i)}, y_w^{(i)}, y_l^{(i)}\}_{i=1}^N\)에 대한 액세스를 가정하면 reward model을 $r_\phi(x, y)$로 parameterize하고 maximum likelihood를 통해 파라미터를 추정할 수 있다. 문제를 이진 분류(binary classification)로 구성하면 negative log-likelihood loss는 다음과 같다.
\[\begin{equation} \mathcal{L}_R (r_\phi, \mathcal{D}) = - \mathbb{E}_{(x, y_w, y_l) \sim \mathcal{D}} [\log \sigma (r_\phi (x, y_w) - r_\phi (x, y_l))] \end{equation}\]여기서 $\sigma$는 로지스틱 함수이다. $r_\phi(x, y)$는 SFT 모델 $\pi^\textrm{SFT} (y \vert x)$에서 초기화되며 최종 transformer layer 위에 linear layer를 추가하여 reward 값에 대한 하나의 스칼라 예측을 생성한다. 낮은 분산의 reward function을 보장하기 위해 이전 연구들에서는 모든 $x$에 대해 \(\mathbb{E}_{(x, y) \sim \mathcal{D}} [r_\phi (x, y)] = 0\)이 되도록 reward를 정규화했다.
3. RL fine-tuning 단계
RL 단계에서는 학습된 reward function을 사용하여 LM에 피드백을 제공한다. 특히 다음과 같은 최적화 문제를 사용한다.
\[\begin{equation} \max_{\pi_\theta} \mathbb{E}_{x \sim \mathcal{D}, y \sim \pi_\theta (y \vert x)} [r_\phi (x, y)] - \beta \mathbb{D}_\textrm{KL} [\pi_\theta (y \vert x) \;\|\; \pi_\textrm{ref} (y \vert x)] \end{equation}\]여기서 $\beta$는 기본 레퍼런스 policy $\pi_\textrm{ref}$, 즉 초기 SFT 모델 $\pi^\textrm{SFT}$와의 편차를 제어하는 파라미터이다. 실제로 LM policy $\pi_\theta$도 $\pi^\textrm{SFT}$로 초기화된다. 추가된 제약 조건은 reward model의 분포에서 모델이 너무 멀리 벗어나는 것을 방지할 뿐만 아니라 생성 다양성을 유지하고 하나의 높은 reward 답변으로의 mode-collapse를 방지하기 때문에 중요하다. 언어 생성의 이산적인 특성으로 인해 이 목적 함수는 미분 가능하지 않으며 일반적으로 강화 학습을 통해 최적화된다. 표준 접근 방식은 reward를
\[\begin{equation} r(x, y) = r_\phi (x, y) − \beta (\log \pi_\theta (y \vert x) − \log \pi_\textrm{ref} (y \vert x)) \end{equation}\]로 구성하고 PPO를 사용하여 최대화하는 것이었다.
Direct Preference Optimization

LM fine-tuning과 같은 대규모의 문제에 RL 알고리즘을 적용하는 것이 어렵기 때문에 본 논문은 선호도를 직접 사용하여 policy를 최적화 하는 간단한 접근 방식을 도출하는 것을 목표로 하였다. Reward를 학습한 후 RL을 통해 최적화하는 이전 RLHF 방법과 달리 본 논문의 접근 방식은 reward 모델링 단계를 피하고 선호도 데이터를 사용하여 언어 모델을 직접 최적화한다. 핵심 통찰력은 reward function에서 최적의 policy로의 수치적 매핑을 활용하여 reward function에 대한 loss function을 policy에 대한 loss function으로 변환할 수 있다는 것이다. 이 change-of-variables 접근 방식을 사용하면 Bradley-Terry 모델과 같은 기존 인간 선호도 모델에서 계속 최적화하면서 명시적인 reward 모델링 단계를 건너뛸 수 있다. 본질적으로 policy 네트워크는 언어 모델과 reward를 모두 나타낸다.
DPO 목적 함수 유도
일반적인 reward function $r$ 하에서 이전 연구들과 동일한 RL 목적 함수로 시작한다. KL 제약 조건을 가지는 reward 최대화 목적 함수에 대한 최적해는 다음과 같은 형식을 취한다.
\[\begin{equation} \pi_r (y \vert x) = \frac{1}{Z (x)} \pi_\textrm{ref} (y \vert x) \exp \bigg( \frac{1}{\beta} r(x, y) \bigg) \\ \textrm{where} \; Z(x) = \sum_y \pi_\textrm{ref} (y \vert x) \exp \bigg( \frac{1}{\beta} r(x, y) \bigg) \end{equation}\]Ground-truth reward function $r^\ast$의 MLE 추정 $r_\phi$를 사용하더라도 여전히 partition function $Z(x)$를 추정하기 어렵기 때문에 이 표현을 실제로 활용하기 어렵다. 그러나 위 식을 재배열하여 최적 policy $\pi_r$, 레퍼런스 policy $\pi_\textrm{ref}$, $Z(\cdot)$의 관점에서 reward function을 표현할 수 있다.
\[\begin{equation} r(x, y) = \beta \log \frac{\pi_r (y \vert x)}{\pi_\textrm{ref} (y \vert x)} + \beta \log Z(x) \end{equation}\]이 reparameterization을 ground-truth reward $r^\ast$와 최적 모델 $π^\ast$에 적용할 수 있다. 다행히도 Bradley-Terry 모델은 두 응답 간의 reward 차이에만 의존한다.
\[\begin{equation} p^\ast (y_1 \succ y_2 \vert x) = \sigma (r^\ast (x, y_1) - r^\ast (x, y_2)) \end{equation}\]$r^\ast (x,y)$에 대한 위 식의 reparameterization을 선호도 모델에 대입하면 $Z$가 사라지고 $\pi^\ast$와 $\pi_\textrm{ref}$만으로 선호도 확률을 표현할 수 있다. 따라서 Bradley-Terry 모델에 따른 최적의 RLHF policy $\pi^\ast$는 다음과 같은 선호도 모델을 만족한다.
\[\begin{equation} p^\ast (y_1 \succ y_2 \vert x) = \bigg( 1 + \exp \bigg( \beta \log \frac{\pi^\ast (y_2 \vert x)}{\pi_\textrm{ref} (y_2 \vert x)} - \beta \log \frac{\pi^\ast (y_1 \vert x)}{\pi_\textrm{ref} (y_1 \vert x)} \bigg) \bigg)^{-1} \end{equation}\]Reward model이 아닌 최적 policy 측면에서 선호도 데이터의 확률을 얻었으므로 parameterize된 policy $\pi_\theta$에 대한 maximum likelihood 목적 함수를 다음과 같이 공식화할 수 있다.
\[\begin{equation} \mathcal{L}_\textrm{DPO} (\pi_\theta; \pi_\textrm{ref}) = -\mathbb{E}_{(x, y_w, y_l) \sim \mathcal{D}} \bigg[ \log \sigma \bigg( \beta \log \frac{\pi_\theta (y_w \vert x)}{\pi_\textrm{ref} (y_w \vert x)} - \beta \log \frac{\pi_\theta (y_l \vert x)}{\pi_\textrm{ref} (y_l \vert x)} \bigg) \bigg] \end{equation}\]이러한 방식을 사용하면 명시적인 reward 모델링 단계를 피하는 동시에 강화 학습 최적화를 수행할 필요도 없다. 또한 reparameterize된 Bradley-Terry 모델을 피팅하는 것과 동일하기 때문에 선호도 데이터 분포의 적절한 가정 하에서 일관성과 같은 특정 이론적 특성을 유지한다.
DPO 업데이트는 무엇을 하는가?
파라미터 $\theta$에 대한 loss function \(\mathcal{L}_\textrm{DPO}\)의 기울기는 다음과 같다.
\[\begin{equation} \nabla_\theta \mathcal{L}_\textrm{DPO} (\pi_\theta; \pi_\textrm{ref}) = -\beta \mathbb{E}_{(x, y_w, y_l) \sim \mathcal{D}} \bigg[ \sigma(\hat{r}_\theta (x, y_l) - \hat{r}_\theta (x, y_w)) \bigg[ \nabla_\theta \log \pi (y_w \vert x) - \nabla_\theta \log \pi (y_l \vert x) \bigg] \bigg] \\ \textrm{where} \; \hat{r}_\theta (x, y) = \beta \log \frac{\pi_\theta (y \vert x)}{\pi_\textrm{ref} (y \vert x)} \end{equation}\]\(\hat{r}_\theta (x, y)\)는 언어 모델 $\pi_\theta$와 레퍼런스 모델 \(\pi_\textrm{ref}\)에 의해 암시적으로 정의된 reward이다. $\nabla_\theta \log \pi (y_w \vert x)$는 $y_w$의 likelihood를 증가시키고 $\nabla_\theta \log \pi (y_l \vert x)$는 $y_l$의 likelihood를 감소시킨다. Reward 추정이 잘못된 경우 가중치 \(\sigma(\hat{r}_\theta (x, y_l) - \hat{r}_\theta (x, y_w))\)가 커진다. 즉 암시적 reward model이 KL 제약의 강도를 고려하여 응답이 얼마나 잘못 정렬되는지에 따라 가중치가 결정된다는 것이다.
Experiments
- Task
- 제어된 감정 생성
- IMDb 데이터셋
- $x$는 영화 리뷰의 앞부분, $y$는 긍정적인 감정의 영화 리뷰
- 요약
- Reddit TL;DR 요약 데이터셋
- $x$는 Reddit의 게시물, $y$는 게시물의 주요 요점에 대한 요약
- Single-turn 대화
- Anthropic Helpful and Harmless 대화 데이터셋
- $x$는 사람의 질문, $y$는 질문에 대해 매력적이고 유용한 응답
- 제어된 감정 생성
저자들은 평가에 대해 두 가지 다른 접근 방식을 사용하였다.
- 제어된 감정 생성 task의 경우 reward의 경계와 레퍼런스 모델에 대한 KL divergence를 기준으로 각 알고리즘을 평가한다. 이 경계는 ground-truth reward function(감정 분류기)에 접근할 수 있기 때문에 계산 가능하다.
- 요약과 single-turn 대화의 경우 ground-truth reward function이 알려져 있지 않다. 따라서 각각 요약 품질과 응답 유용성에 대한 사람의 평가의 대체재로 GPT-4를 사용하여 baseline에 대한 승률로 알고리즘을 평가한다. 요약의 경우 테스트셋의 레퍼런스 요약을 baseline으로 사용한다. 대화의 경우 테스트셋에서 선호하는 응답을 baseline으로 사용한다.
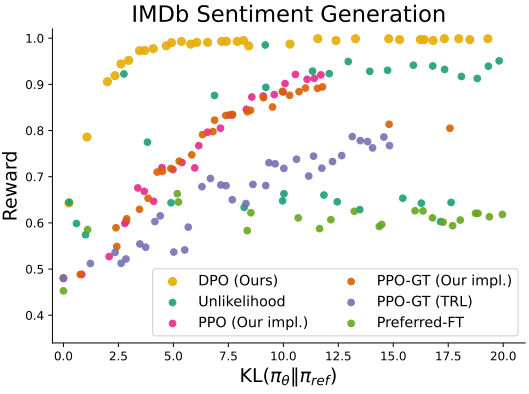
다음은 IMDb 감정 생성 task에 대한 결과이다.
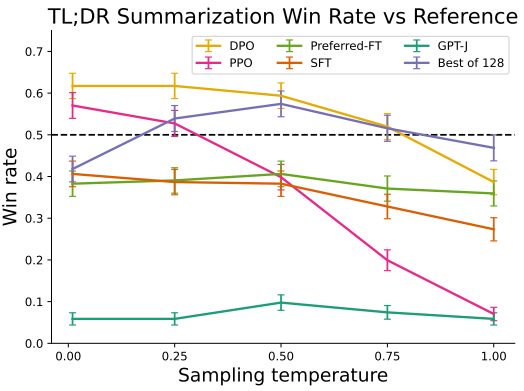
다음은 TL;DR 요약 task에 대한 승률이다.
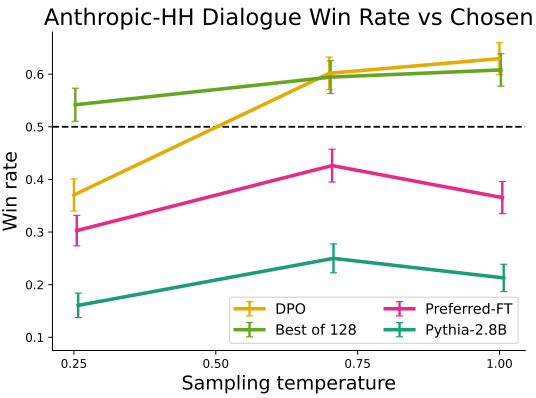
Anthropic-HH 대화 task에 대한 승률이다.
다음은 fine-tuning step에 따른 대화 task에 대한 승률 변화이다.

저자들은 GPT-4 사용을 정당화하기 위해 추가로 human study를 수행하였다. GPT-4 (S) 프롬프트는 게시물의 중요한 정보를 더 잘 요약하는 것이 어떤 요약을 묻는다. GPT-4는 더 길고 더 반복적인 요약을 선호하므로 어떤 요약이 더 간결한지도 묻는 GPT-4 (C) 프롬프트도 함께 평가하였다. Human study 결과는 아래 표와 같다.
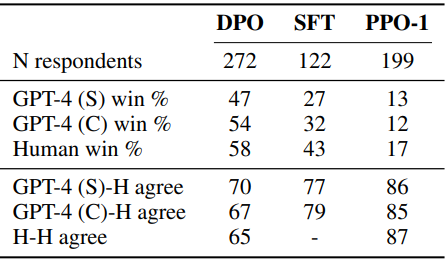
GPT-4 판단이 사람의 판단과 강한 상관관계가 있음을 알 수 있다. GPT-4와 사람 사이의 일치율은 사람과 사람 사이의 일치율과 비슷하거나 오히려 더 높다.