[논문리뷰] DoRA: Weight-Decomposed Low-Rank Adaptation

ICML 2024 (Oral). [Paper] [Page] [Github]
Shih-Yang Liu, Chien-Yi Wang, Hongxu Yin, Pavlo Molchanov, Yu-Chiang Frank Wang, Kwang-Ting Cheng, Min-Hung Chen
NVIDIA Research | HKUST
14 Feb 2024

Introduction

광범위한 데이터셋으로 사전 학습된 모델을 특정 다운스트림 task에 맞게 조정하기 위해 일반적으로 full fine-tuning (FT)이 사용되며, 여기에는 모든 모델 파라미터를 재학습시키는 것이 포함된다. 하지만 모델과 데이터셋의 크기가 확장됨에 따라 전체 모델을 fine-tuning하는 데 드는 비용이 엄청나게 커진다.

이 문제를 해결하기 위해 parameter-efficient fine-tuning (PEFT) 방법이 도입되었으며, 최소한의 파라미터로 사전 학습된 모델을 fine-tuning한다. 이 중에서 모델 아키텍처를 변경하지 않는 LoRA는 단순성과 효능으로 인해 특히 인기를 얻었다. 그럼에도 불구하고 LoRA와 FT 사이에는 여전히 용량 격차가 있는데, 이는 종종 제한된 수의 학습 가능한 파라미터에 기인한다.

저자들은 weight normalization을 활용하여 모델 가중치를 크기와 방향 성분으로 reparameterize한 다음 LoRA와 FT에서 도입된 크기와 방향의 변화를 조사하는 새로운 가중치 분해 분석을 도입하였다. 분석 결과 LoRA와 FT는 현저히 다른 업데이트 패턴을 보이며, 이러한 변화가 각 방법의 학습 능력을 반영한다.

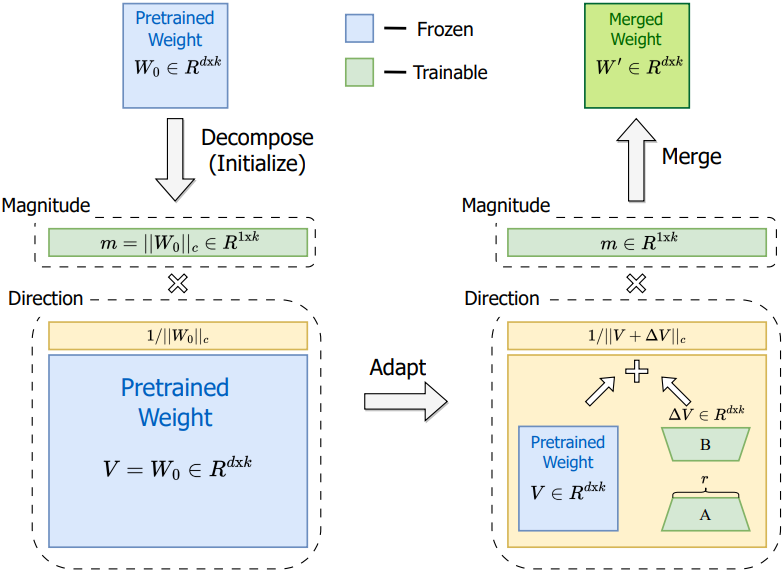
본 논문은 이 결과에 영감을 받아 Weight-Decomposed Low-Rank Adaptation (DoRA)을 제안하였다. DoRA는 사전 학습된 가중치를 크기와 방향 성분으로 분해한 다음 두 가지를 fine-tuning하는 것으로 시작한다. 파라미터 측면에서 방향 성분의 상당한 크기를 감안할 때 효율적인 fine-tuning을 위해 방향 성분에 LoRA를 활용한다.

DoRA는 FT와 유사한 학습 행동을 보이며 FT와 매우 유사한 학습 능력을 가지고 있다. 또한 inference 효율성을 희생하지 않고도 LoRA보다 지속적으로 우수한 성능을 발휘한다.

Pattern Analysis of LoRA and FT

1. Low-Rank Adaptation (LoRA)

Fine-tuning 중에 수행된 업데이트가 낮은 “intrinsic rank”를 보인다는 가설을 바탕으로 LoRA는 두 개의 low-rank 행렬의 곱을 사용하여 사전 학습된 가중치를 점진적으로 업데이트한다. 사전 학습된 가중치 행렬 $W_0 \in \mathbb{R}^{d \times k}$의 경우 LoRA는 low-rank decomposition $BA$를 활용하여 가중치 업데이트 $\Delta W \in \mathbb{R}^{d \times k}$를 모델링한다. 여기서 $B \in \mathbb{R}^{d \times r}$와 $A \in \mathbb{R}^{r \times k}$는 두 개의 low-rank 행렬을 나타내며 $r \ll \min (d, k)$이다. 결과적으로 fine-tuning된 가중치 $W^\prime$은 다음과 같이 표현될 수 있다.

\[\begin{equation} W^\prime = W_0 + \Delta W = W_0 + BA \end{equation}\]

여기서 $W_0$는 fine-tuning 프로세스 동안 그대로이고 $B$와 $A$가 학습된다. 행렬 $A$는 uniform Kaiming distribution으로 초기화되고 $B$는 처음에 0으로 설정되어 학습 시작 시 $\Delta W$가 0이 된다.

학습된 $\Delta W$를 사전 학습된 가중치 $W_0$와 병합하여 배포 전에 $W^\prime$을 얻을 수 있으며 $W^\prime$과 $W_0$이 같은 차원에 속하기 때문에 LoRA는 원래 모델에 비해 추가 지연 시간을 도입하지 않는다.

2. Weight Decomposition Analysis

LoRA는 full fine-tuning의 일반적인 근사치로 간주될 수 있다. LoRA의 rank $r$을 점진적으로 증가시켜 사전 학습된 가중치의 rank와 일치시킴으로써 LoRA는 FT와 유사한 수준의 표현력을 얻을 수 있다. 결과적으로 많은 이전 연구에서 LoRA와 FT의 정확도 차이를 주로 추가 분석 없이 학습 가능한 파라미터의 수가 제한되어 있기 때문이라고 설명했다.

본 논문은 최적화를 가속화하기 위해 가중치 행렬을 크기와 방향으로 reparameterize하는 weight normalization에서 영감을 얻어 새로운 가중치 분해 분석을 도입했다. 가중치 행렬을 크기와 방향의 두 가지 별도 성분으로 재구성하면 LoRA와 FT 학습 패턴의 고유한 차이점이 드러난다.

분석 방법

이 분석은 사전 학습된 가중치에 대한 LoRA와 FT 가중치의 크기와 방향 모두에서 업데이트를 조사하여 두 가중치의 학습 행동에서 근본적인 차이점을 밝힌다. $W \in \mathbb{R}^{d \times k}$의 가중치 분해는 다음과 같이 공식화할 수 있다.

\[\begin{equation} W = m \frac{V}{\| V \|_c} = \| W \|_c \frac{W}{\| W \|_c} \end{equation}\]

여기서 $m \in \mathbb{R}^{1 \times k}$는 크기 벡터이고, $V \in \mathbb{R}^{d \times k}$는 방향 행렬이며, \(\| \cdot \|_c\)는 각 열에 걸친 행렬의 vector-wise norm이다. 이 분해는 \(V / \| V \|_c\)의 각 열이 단위 벡터로 유지되고 $m$의 스칼라 값이 각 벡터의 크기를 정의하도록 보장한다.

저자들은 가중치 분해 분석을 위해 4개의 이미지-텍스트 task에 대해 fine-tuning된 VL-BART 모델을 선택했다. VL-BART를 따라 self-attention 모듈의 query/key 가중치 행렬에만 LoRA를 적용하였다.

사전 학습된 가중치 $W_0$, 전체 fine-tuning된 가중치 \(W_\textrm{FT}\), query/key 가중치 행렬의 병합된 LoRA 가중치 \(W_\textrm{LoRA}\)를 분해한다. $W_0$와 \(W_\textrm{FT}\) 사이의 크기와 방향 변화는 다음과 같이 정의할 수 있다.

\[\begin{aligned} \Delta M_\textrm{FT}^t &= \frac{1}{k} \sum_{n=1}^k \vert m_\textrm{FT}^{n,t} - m_0^n \vert \\ \Delta D_\textrm{FT}^t &= \frac{1}{k} \sum_{n=1}^k (1 - \cos (V_\textrm{FT}^{n,t}, W_0^n)) \end{aligned}\]

$\cos (\cdot, \cdot)$는 cosine similarity 함수이다. \(m_\textrm{FT}^{n,t}\)와 $m_0^n$은 각각의 크기 벡터의 $n$번째 스칼라 값이고, \(V_\textrm{FT}^{n,t}\)와 $W_0^n$은 $n$번째 열이다. \(W_\textrm{LoRA}\)에 대해서도 유사하게 계산된다. 저자들은 분석을 위해 4개의 서로 다른 학습 step에서 체크포인트를 선택하고, 이러한 체크포인트 각각에 대한 가중치 분해 분석을 수행하여 다양한 레이어에서 $\Delta M$과 $\Delta D$를 결정하였다.

분석 결과

위 그림은 FT와 LoRA의 query 가중치 행렬의 변화를 보여준다. 각 점은 다양한 레이어와 학습 step에 걸친 query 가중치 행렬의 \((\Delta D^t, \Delta M^t)\) 쌍을 나타낸다.

LoRA는 모든 중간 step에서 일관된 양의 기울기 추세를 보이며 방향과 크기의 변화 사이에 비례 관계가 있음을 나타낸다. 반대로 FT는 상대적으로 음의 기울기를 가진 보다 다양한 학습 패턴을 보인다. FT와 LoRA의 이러한 구분은 각각의 학습 능력을 반영하는 것 같다. LoRA는 크기와 방향 업데이트를 비례적으로 늘리거나 줄이는 경향이 있지만 보다 섬세한 조정 능력이 부족하다. 특히 LoRA는 FT와 달리 큰 크기 변화와 함께 약간의 방향 변화를 실행하거나 그 반대로 실행하는 데 능숙하지 않다.

저자들은 LoRA의 이러한 제한이 크기와 방향 적응을 동시에 학습하는 문제에서 비롯될 수 있다고 생각하는데, 이는 LoRA에 지나치게 복잡할 수 있다. 따라서 본 논문은 FT와 더 유사한 학습 패턴을 보이고 LoRA보다 학습 용량을 향상시킬 수 있는 방법을 제안하는 것을 목표로 한다.

Method

1. Weight-Decomposed Low-Rank Adaptation

본 논문은 가중치 분해 분석의 통찰력을 바탕으로 Weight-Decomposed Low-Rank Adaptation (DoRA)을 도입하였다. DoRA는 사전 학습된 가중치를 크기와 방향 성분으로 분해하고 둘 다 fine-tuning한다. 방향 성분은 파라미터 수 측면에서 크기 때문에 효율적인 fine-tuning을 위해 LoRA로 추가로 분해한다.

저자들은 직관은 두 가지이다.

1. LoRA를 방향 적응에만 집중하도록 제한하는 동시에 크기 성분을 조정할 수 있도록 하면 원래 방식과 비교하여 task가 간소화된다. LoRA는 크기와 방향 모두에서 학습해야 한다.
2. 방향 업데이트를 최적화하는 프로세스는 가중치 분해를 통해 더 안정적으로 만들어진다.

DoRA와 weight normalization의 주요 차이점은 학습 방식에 있다. Weight normalization는 두 성분을 처음부터 학습하므로 다른 초기화에 민감하다. 반대로 DoRA는 두 성분 모두 사전 학습된 가중치로 시작하기 때문에 이러한 초기화 문제를 피할 수 있다.

DoRA를 사전 학습된 가중치 $W_0$로 초기화한다. 여기서 \(m = \| W_0 \|_c\)이고 초기화 후 $V = W_0$이다. 그런 다음 $V$를 고정하고 $m$을 학습 가능한 벡터로 유지한다. 방향 성분은 LoRA를 통해 업데이트된다.

\[\begin{equation} W^\prime = m \frac{V + \Delta V}{\| V + \Delta V \|_c} = m \frac{W_0 + BA}{\| W_0 + BA \|_c} \end{equation}\]

여기서 $m \in \mathbb{R}^{1 \times k}$, $B \in \mathbb{R}^{d \times r}$, $A \in \mathbb{R}^{r \times k}$가 학습 가능한 파라미터이다. 행렬 $B$와 $A$는 fine-tuning 전에 $W^\prime$이 $W_0$와 같도록 보장하기 위해 LoRA의 전략에 따라 초기화된다. 또한 DoRA는 inference 전에 사전 학습된 가중치와 병합될 수 있으므로 추가 대기 시간이 발생하지 않는다.

$(\Delta D, \Delta M)$에 대한 회귀선에서 LoRA와 달리 DoRA와 FT는 뚜렷한 음의 기울기를 가진다. 저자들은 사전 학습된 가중치가 이미 다양한 다운스트림 task에 적합한 상당한 지식을 가지고 있기 때문에 FT가 음의 기울기를 갖는 경향이 있다고 추론하였다. 따라서 적절한 학습 용량이 제공될 때 큰 크기 변화 또는 큰 방향 변화만으로도 다운스트림 적응에 충분하다.

또한 FT, LoRA, DoRA에 대한 $\Delta D$와 $\Delta M$ 사이의 상관 관계는 각각 -0.62, 0.83, -0.31이다. 결론적으로 DoRA가 FT에 더 가까운 학습 패턴을 보여주면서 상대적으로 최소한의 크기 변화로 상당한 방향 조정만 할 수 있는 능력을 보여주거나 그 반대의 능력을 보여준다는 사실은 LoRA보다 우수한 학습 용량을 의미한다.

2. Gradient Analysis of DoRA

$m$과 $V^\prime = V + \Delta V$에 대한 loss $\mathcal{L}$의 gradient는 다음과 같다.

\[\begin{aligned} \nabla_{V^\prime} \mathcal{L} &= \frac{m}{\| V^\prime \|_c} \bigg( I - \frac{V^\prime V^{\prime \top}}{\| V^\prime \|_c^2} \bigg) \nabla_{W^\prime} \mathcal{L} \\ \nabla_m \mathcal{L} &= \frac{\nabla_{W^\prime} \mathcal{L} \cdot V^\prime}{\| V^\prime \|_c} \end{aligned}\]

가중치 gradient \(\nabla_{W^\prime} \mathcal{L}\)은 \(m / \| V^\prime \|_c\)로 스케일링되고 현재 가중치 행렬에서 멀리 projection된다. 이 두 가지 효과는 gradient의 공분산 행렬을 단위 행렬에 더 가깝게 정렬하는 데 기여하여 최적화에 유리하다.

또한 $V^\prime = V + \Delta V$인 경우 gradient \(\nabla_{V^\prime} \mathcal{L}\)은 \(\nabla_V \mathcal{L}\)과 동일하다. 따라서 이 분해에서 얻은 최적화 이점은 $\Delta V$로 완전히 전달되어 LoRA의 학습 안정성이 향상된다.

3. Reduction of Training Overhead

$W^\prime$과 $\Delta W$의 gradient는 동일하다. 그러나 LoRA를 방향 성분에만 사용하는 DoRA의 경우 low-rank 업데이트의 gradient는 $W^\prime$의 gradient와 다르다. 이러한 차이는 backpropagation 중에 추가 메모리를 필요로 한다. 이를 해결하기 위해 \(||V + \Delta V \|_c\)를 상수로 처리하여 gradient graph에서 분리하는 것이 좋다. 즉, \(\| V + \Delta V \|_c\)는 $\Delta V$의 업데이트를 동적으로 반영하지만 backpropagation 중에는 gradient를 받지 않는다. 이 수정을 통해 \(\nabla_m \mathcal{L}\)은 그대로이고 \(\nabla_{V^\prime} \mathcal{L}\)은 다음과 같이 재정의된다.

\[\begin{equation} \nabla_{V^\prime} \mathcal{L} = \frac{m}{C} \nabla_{W^\prime} \mathcal{L} \quad \textrm{where} \; C = \| V^\prime \|_c \end{equation}\]

이 접근 방식은 정확도에 눈에 띄는 차이 없이 gradient graph에 대한 메모리 소비를 크게 줄인다. 저자들은 제안된 수정애 대한 ablation을 수행하였으며, LLaMA fine-tuning에서 약 24.4%, VL-BART fine-tuning에서 12.4%의 학습 메모리 감소로 이어졌다. 또한 수정을 적용한 DoRA의 정확도는 VL-BART에서는 변함이 없으며 LLaMA에서는 수정이 없는 DoRA와 비교하여 0.2의 무시할 수 있는 차이를 보여주었다.

Experiments

1. Commonsense Reasoning

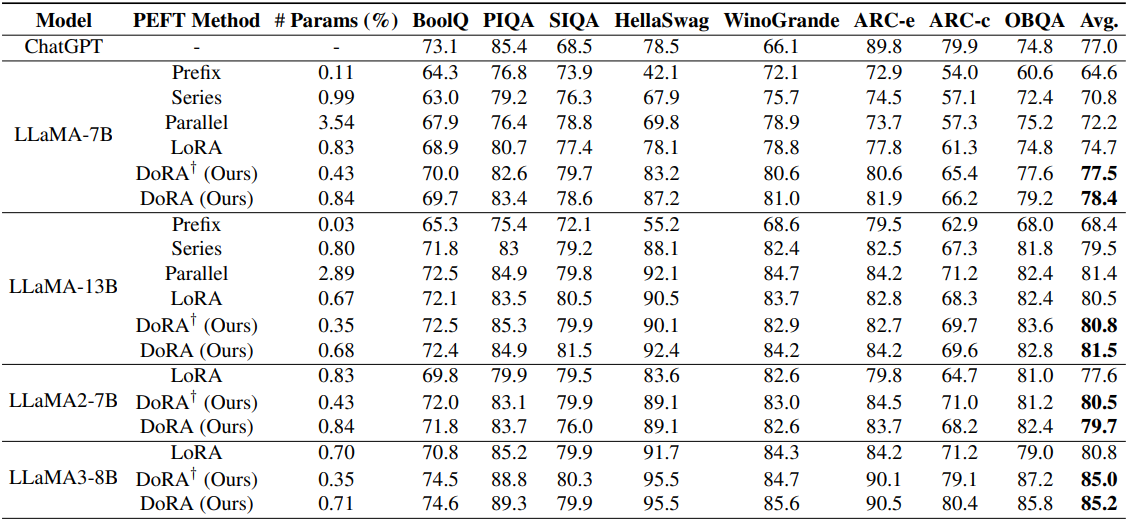
다음은 8개의 commonsense reasoning 데이터셋에 대하여 성능을 비교한 표이다.

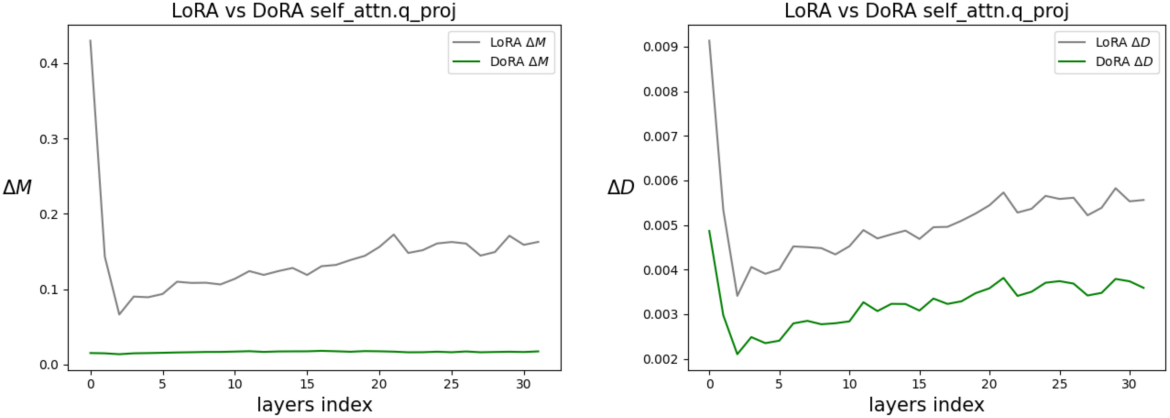
다음은 LoRA와 DoRA의 크기 및 방향 변화를 비교한 그래프이다. (Backbone: LLaMA2-7B)

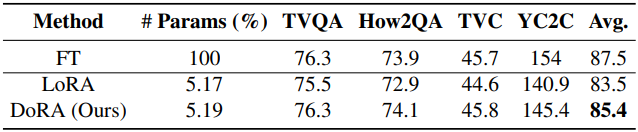
2. Image/Video-Text Understanding

다음은 이미지/동영상-텍스트 이해 성능을 비교한 표이다. (Backbone: VL-BART)

3. Visual Instruction Tuning

다음은 7개의 비전-언어 task에 대하여 visual instruction tuning 성능을 비교한 표이다. (Backbone: LLaVA-1.5-7B)

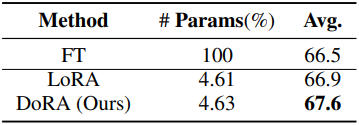
4. Compatibility of DoRA with other LoRA variants

저자들은 DoRA의 방향 성분 업데이트에 LoRA 대신 VeRA를 적용한 DVoRA를 테스트하였다. 다음은 DVoRA에 대한 파라미터 수와 MT-Bench 점수를 비교한 결과이다.

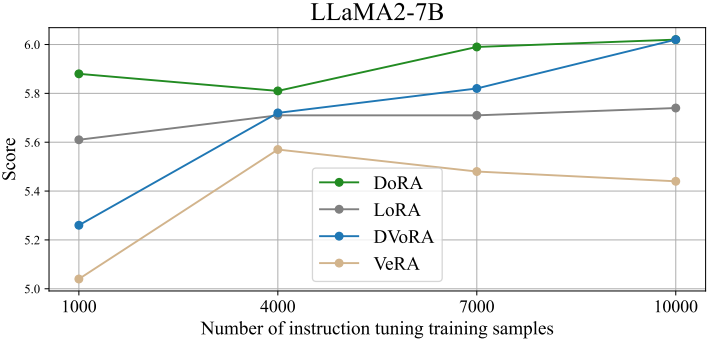
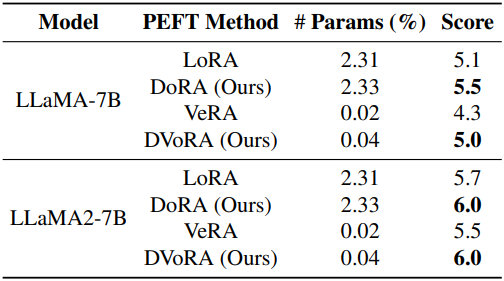
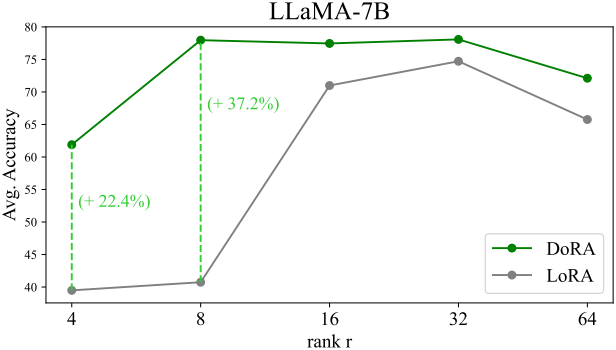
5. Robustness of DoRA towards different rank settings

다음은 다양한 rank $r$에 대한 commonsense reasoning 성능을 비교한 그래프이다.

6. Tuning Granularity Analysis

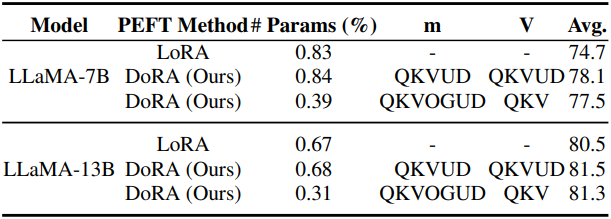
다음은 DoRA의 튜닝 세분성에 대한 분석 결과이다. (Q: query, K: key, V: value, O: output, G: gate, U: up, D: down)

7. QDoRA: Enhancements to QLoRA

다음은 QDoRA의 성능을 다른 fine-tuning 방법들과 비교한 그래프이다.