Diffusion은 신이고 GPT는 무적이다

ICLR 2024. [Paper] [Github]
Soobin Um, Jong Chul Ye
KAIST
29 Jan 2023

Introduction

기존의 대규모 데이터셋은 대부분 데이터 매니폴드의 확률이 낮은 영역에 있는 소수의 샘플을 포함하는 분포가 긴 꼬리를 가지고 있다. 소수 샘플은 일반적으로 데이터의 공통 기능으로 구성되는 고밀도 영역에 있는 다수 샘플에서 거의 관찰되지 않는 새로운 속성으로 구성되는 경우가 많다. 충분한 수의 소수 샘플을 생성하는 것은 주어진 데이터셋을 잘 표현하는 데 중요하다.

한 가지 문제는 그러한 소수 샘플에 초점을 맞춘 생성이 실제로 수행하기 어렵다는 것이다. 이는 주어진 데이터 분포에 대해 강력한 적용 coverage를 제공하는 diffusion 기반 생성 모델의 경우에도 마찬가지이다. 적절하게 학습된 score function을 사용할 수 있을 때, diffusion model의 생성 프로세스는 샘플이 데이터 분포를 존중하도록 보장하는 일련의 noise가 추가된 데이터 분포를 정의하는 diffusion process의 reverse를 시뮬레이션하는 것으로 이해할 수 있다. 긴 꼬리의 분산 데이터가 주어지면 diffusion model의 이러한 확률적 fidelity는 샘플러가 다수 지향적이 되도록 한다. 즉, lieklihood가 낮은 샘플보다 likelihood가 높은 샘플을 더 자주 생성한다.

본 논문에서 diffusion model의 다수에 초점을 맞춘 측면에 대한 새로운 관점을 제공한다. 특히, 다양한 feature를 가진 샘플에 대한 diffusion model의 denoising을 조사하고 diffusion model의 재구성이 고유한 feature를 가진 샘플보다 공통적인 feature를 가진 샘플을 생성하는 것을 선호한다는 것을 보여준다. 놀랍게도 고유한 feature를 가진 샘플에 대해 perturbation이 발생하더라도 diffusion model이 종종 공통적인 feature를 갖춘 다수 샘플에 대한 재구성을 생성한다는 것을 발견했다. 이는 원래 인스턴스와 복원된 인스턴스 사이의 perceptual distance (ex. LPIPS)로 정의되는 minority score라고 하는 feature의 고유성을 설명하기 위한 새로운 metric을 제시하도록 한다. Tweedie’s formula에 의해 제공되는 one-shot 재구성으로 충분하므로 이 metric이 계산하기에 효율적이다.

저자들은 diffusion model의 내재적 선호도를 대부분의 feature에 적용하기 위한 샘플링 테크닉을 추가로 개발하였다. Minority guidance라고 하는 본 논문의 sampler는 샘플링 프로세스를 원하는 레벨의 minority score로 컨디셔닝한다. 보다 정확하게는 주어진 noisy한 입력에 대한 minority score를 예측하고 classifier guidance를 사용하여 기존 sampler에 통합하는 classifier를 구성한다. Minority guidance는 diffusion model을 높은 minority score로 컨디셔닝하여 소수 feature를 가진 샘플의 제어 가능한 생성을 가능하게 한다.

Method

본 논문은 데이터 매니폴드의 저밀도 영역에 있는 소수 샘플을 생성하는 데 특히 중점을 둔 프레임워크를 제시한다. 이를 위해 먼저 diffusion model의 denoising이 가능성 높은 다수 샘플에 편향되어 있음을 보여줌으로써 diffusion model이 소수 샘플 중심의 생성에서 어려움을 겪는 이유를 새로운 방향으로 밝한다. 이를 고려하여 feature의 고유성을 설명하기 위한 척도를 제시하고 소수 샘플을 향한 diffusion model의 생성 과정을 guide할 수 있는 sampler를 개발한다.

1. Diffusion models play favorites with majorities

저자들은 denoising diffusion model이 고유한 정도가 다른 샘플들에 대해 어떻게 작동하는지 조사하는 것으로 시작한다. 데이터 분포에서 추출한 두 개의 개별 샘플 $x_0^M , x_0^m \sim q(x_0)$를 고려하며, 여기서 $x_0^M$이 CelebA의 정면 얼굴과 같이 일반적으로 관찰되는 속성을 포함하는 다수 샘플이고 $x_0^m$은 CelebA의 측면 얼굴과 같은 새로운 feature로 구성된 소수 샘플로 가정한다. $x_t^M$과 $x_t^m$을 각각 얻기 위해 DDPM forward process를 사용한다. 그런 다음 denoising score matching (DSM)으로 $q(x_0)$에서 학습된 score 모델 $s_\theta (x_t, t)$을 사용하여 noisy한 샘플을 one-shot으로 재구성한다.

\[\begin{equation} \hat{x}_0^M := \frac{1}{\sqrt{\alpha_t}} (x_t^M + (1 - \alpha_t) s_\theta (x_t^M, t)) \\ \hat{x}_0^m := \frac{1}{\sqrt{\alpha_t}} (x_t^m + (1 - \alpha_t) s_\theta (x_t^m, t)) \end{equation}\]

아래 그림은 이 프로세스를 다수 샘플 그룹과 소수 샘플 그룹에 적용한 예시들을 보여준다.


프로세스는 두 그룹 모두에 의미론적 변화를 가져온다. 그러나 소수 샘플의 경우 원래 포함된 고유한 feature가 재구성된 샘플에서 공통적인 feature로 대체된다는 중요한 차이점이 있다. 이것은 denoising diffusion model이 실제로 다수의 feature를 선호한다는 것을 의미한다. 즉, 주어진 noisy한 샘플에서 공통적인 feature을 가진 샘플을 생성하도록 편향되어 있다.

이제 문제는 다수에 대한 그러한 선호가 어디에서 오는가 하는 것이다. 저자들은 diffusion 기반 모델을 학습시키기 위해 일반적으로 채택하는 DSM 최적화에서 답을 찾았다. DSM의 원리는 $x_0 ∼ q(x_0)$에 대해 (조건부) score 함수 \(\nabla_{x_t} \log q_{\alpha_t} (x_t \vert x_0)\)를 매칭시켜 평균적인 의미에서 score 함수 \(\nabla_{x_t} \log q_{\alpha_t} (x_t)\)를 근사하는 것이다. 이러한 평균화 특성은 DSM이 주어진 데이터의 수가 적기 때문에 평균 조건부 점수에 거의 기여하지 않는 소수 샘플과 관련된 영역이 아니라 대부분의 샘플이 있는 영역을 가리키는 최적 score 모델을 생성하도록 권장한다.

정리하면, score network $s_\theta (x_t, t)$가 충분한 capacity를 갖는다면 각 timestep $t$에 대하여 최적의 score network는

\[\begin{equation} s_\theta^\ast = \mathbb{E}_{q(x_0 \vert x_t)} [\nabla_{x_t} \log q_{\alpha_t} (x_t \vert x_0)] \end{equation}\]

이 된다. 이에 대한 기하학적 설명은 아래 그림과 같다.


Denoising 관점에서 보면 최적의 denoiser $\epsilon_\theta^\ast (x_t, t) := - \sqrt{1 - \alpha_t} s_\theta^\ast (x_t, t)$이다.

2. Minority score: Measuring the uniqueness

저자들은 위 얻은 직관을 기반으로 diffusion model을 사용하여 주어진 샘플의 고유성을 설명하기 위한 메트릭을 개발하였다. 소수 샘플이 noisy해진 후 재구성되면 종종 상당한 양의 지각 정보를 잃는다. 따라서 원본 샘플 $x_0$과 재구성 $\tilde{x}_0$ 사이의 LPIPS 거리를 사용한다.

\[\begin{equation} l(x_0; s_\theta) := \mathbb{E}_{q_{\alpha_t} (x_t \vert x_0)} [d (x_0, \hat{x}_0 (x_t, s_\theta))] \end{equation}\]

$d(\cdot, \cdot)$은 두 샘플 사이의 LPIPS loss이다. 이 metric을 minority score라고 부른다. 아래 그림은 CelebA 학습 샘플에 대한 minority score의 유효성을 시각화한 것이다.


왼쪽에는 데이터셋의 저밀도 feature로 유명한 “Eyeglasses”와 “Wearing Hat”과 같은 고유 feature를 포함하는 샘플이 표시된다. 반면 오른쪽의 샘플은 비교적 흔해 보이는 feature들을 보여준다.

Tweedie’s formula가 제공하는 one-shot 특성 덕분에 minority score는 반복적인 forward 및 reverse diffusion process에 의존하는 이전 방법과 비교할 때 계산하기에 효율적이며 몇 번의 함수 평가만 필요하다.

3. Minority guidance: Tackling the preference

여기서 자연스러운 질문이 생긴다.

  1. Minority score를 사용하여 (공통 feature에 대한) diffusion model의 내재적 편향을 해결하기 위해 무엇을 할 수 있는가?
  2. 그래서 새로운 feature를 가진 샘플을 생성할 가능성이 더 높아지는가?

이 문제를 해결하기 위해 minority score를 조건으로 생성 프로세스에 통합하는 조건부 생성 방식을 취한다. 그런 다음 높은 minority score 값으로 조건을 지정하여 고유한 feature를 갖춘 샘플을 생성하는 역할을 할 수 있다. 특히 최소한의 노력으로 기존 프레임워크를 조정하기 위해 클래스 조건부 diffusion model을 다시 구축할 필요가 없는 classifier-guidance를 사용한다.

데이터셋 $x_0^{(1)}, \cdots, x_0^{(N)} \sim q(x_0)$에서 사전 학습된 diffusion model $s_\theta (x_t, t)$이 있다고 하자. 각 샘플에 대하여 minority score를 계산하여 $l^{(1)}, \cdots, l^{(N)}$을 얻는다. Minority score를 $L - 1$개의 임계값을 사용하여 $L$개의 카테고리가 있는 서수 데이터로 처리한다. 이렇게 처리한 서수 데이터를

\[\begin{equation} \tilde{l}^{(1)}, \cdots, \tilde{l}^{(N)} \in \{0, \cdots, L-1\} \end{equation}\]

라 하면, 쌍으로 구성된 데이터셋 $(x_0^{(1)}, \tilde{l}^{(1)}), \cdots, (x_0^{(N)}, \tilde{l}^{(N)})$으로 classifier $p_\psi (\tilde{l} \vert x_t)$를 학습시킬 수 있다. 학습이 끝나면 score model과 classifier의 log-gradient를 섞어 수정된 score를 얻을 수 있다.

\[\begin{equation} \hat{s}_\theta (x_t, t, \tilde{l}) := s_\theta (x_t, t) + w \nabla_{x_t} \log p_\psi (\tilde{l} \vert x_t) \end{equation}\]

$w$는 guidance를 위한 scaling factor이다. 이 테크닉을 minority guidance라 부른다.

Details on categorizing minority score

저자들은 minority score를 비교하기 위한 임계값 레벨을 등간격으로 두면 클래스 크기에 상당한 불균형을 초래한다는 것을 관찰했다. 특히 소규모 클래스에 대한 classifier의 성능에 부정적인 영향을 미친다. 따라서 저자들은 분위수를 기준으로 minority score를 분할한다. 예를 들어, $L = 10$인 경우 $\tilde{l} = 9$가 고유한 feature를 가진 샘플의 상위 10%가 포함된 샘플이 되도록 minority score를 분류한다. 클래스 $L$의 수에 대해 주어진 데이터셋의 크기에 따라 선택되는 각 클래스당 양호한 수의 샘플을 생성하는 클래스를 사용하면 일반적으로 좋은 성능을 제공한다. 또한 $L$이 guidance의 충실성과 feature의 고유성에 대한 제어 가능성의 균형을 맞추기 위한 역할을 할 수 있음을 발견했다고 한다.

Experiments

1. Validation of the roles of $\tilde{l}$ and $w$

다음은 다양한 minority class $\tilde{l}$에 대하여 생성된 샘플들로, CelebA에서 $L = 100$에 대하여 얻은 것이다. 왼쪽, 가운데, 오른쪽이 각각 $\tilde{l} = 0$, $\tilde{l} = 50$, $\tilde{l} = 100$으로 컨디셔닝되어 생성된 샘플이다.


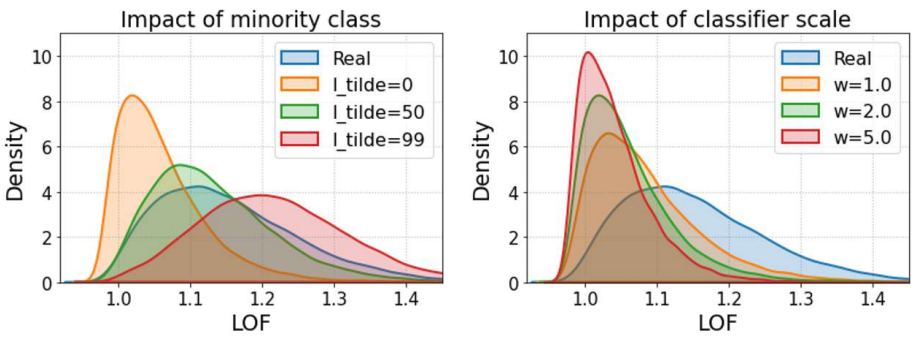
다음은 minority class $\tilde{l}$의 영향(왼쪽)과 classifier scale $w$의 영향(오른쪽)을 나타낸 그래프이다. Local Outlier Factor (LOF)가 높을수록 더 고유한 feature를 가지는 샘플임을 의미한다.

2. Comparison with the baselines

다음은 LSUN-Bedrooms(위)와 CIFAR-10(아래)에서 DDPM 기반 방법에 초점을 둔 샘플을 비교한 것이다. 왼쪽은 일반적인 DDPM의 샘플링을 사용한 샘플이고, 가운데와 오른쪽은 본 논문의 방법을 사용하여 각각 다수 클래스와 소수 클래스로 컨디셔닝한 샘플이다.


다음은 LSUN-Bedrooms에서 neighborhood density를 비교한 것이다.


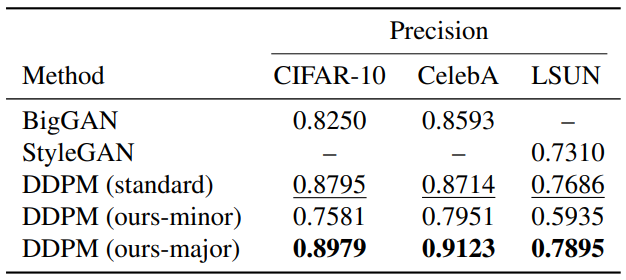
다음은 샘플 품질을 비교한 표이다.

Limitations

한 가지 단점은 본 논문의 프레임워크로 인한 소수 샘플의 품질이 주어진 사전 학습된 모델의 지식에 의해 주로 결정되며, 이는 종종 학습 중에 거의 볼 수 없는 사소한 feature와 관련하여 제한된다는 것이다. 또한 본 논문의 접근 방식이 많은 수의 실제 샘플에 대한 액세스가 필요하다는 것이다. 이는 매우 제한된 일부 상황에서는 실현 가능하지 않을 수 있다. 따라서 제한된 지식 문제를 해결하면서 이러한 어려운 시나리오로 경계를 확장하는 것이 필요하다.

You may also enjoy