[논문리뷰] Domain Expansion of Image Generators

CVPR 2023. [Paper] [Page] [Github]
Yotam Nitzan, Michaël Gharbi, Richard Zhang, Taesung Park, Jun-Yan Zhu, Daniel Cohen-Or, Eli Shechtman
Adobe Research | Tel-Aviv University | Carnegie Mellon University
12 Jan 2023

Introduction

최근의 도메인 적응 기술은 새로운 타겟 도메인에서 이미지를 생성할 수 있도록 사전 학습된 generator를 적응함으로써 현대 생성 이미지 모델의 엄청난 성공에 편승하였다. 종종 타겟 도메인은 원본 도메인과 관련하여 정의된다. 그러한 관계가 유지될 때 도메인 적응은 일반적으로 소스 도메인에서 학습된 변동 요소를 보존하고 이를 새로운 것으로 전송하려고 한다. 그러나 기존 기술을 사용하면 적응된 모델이 원래 도메인에서 이미지를 생성하는 능력을 상실한다.

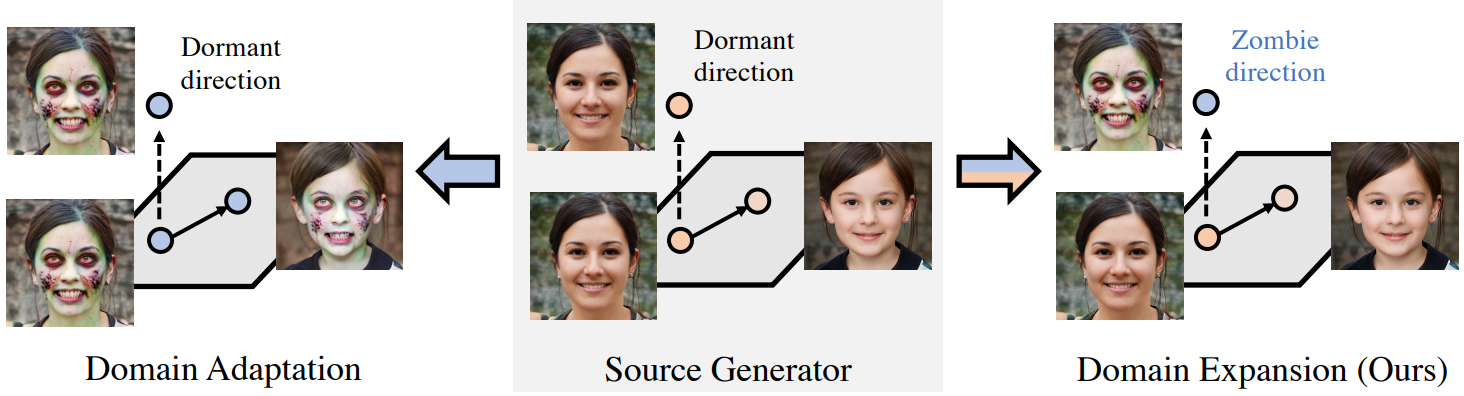
본 논문에서는 domain expansion이라는 새로운 task를 소개한다. 도메인 적응과 달리, 원래 동작을 무시하지 않고 단일 모델이 생성할 수 있는 이미지 공간을 늘리는 것을 목표로 한다. 유사한 이미지 도메인을 분리된 데이터 분포로 보는 대신 결합 분포에서 서로 다른 모드로 취급한다. 결과적으로 도메인은 원래 데이터 도메인에서 상속된 semantic prior를 공유한다. 예를 들어 포즈나 얼굴 모양과 같이 사실적인 얼굴에 내재된 변동 요소는 “좀비” 도메인에도 동일하게 적용될 수 있다.

이를 위해 원래 데이터 도메인을 존중하면서 확장을 위한 모델 학습 프로세스를 신중하게 구성한다. 저차원 latent space가 있는 현대의 생성 모델이 흥미롭고 창발적인 속성을 제공한다는 것은 잘 알려져 있다. 학습을 통해 latent space는 선형적이고 해석 가능한 방식으로 변동 요인을 나타낸다. 이 유리한 동작을 확장하고 선형적이고 disentangle된 방향을 따라 새로운 도메인을 표현하고자 한다. 흥미롭게도 이전 연구들에서 많은 latent 방향이 생성된 이미지에 지각할 수 있는 영향이 미미한 것으로 나타났다. 이 결과를 활용하여 이러한 방향을 새로운 도메인을 나타내도록 용도 변경한다.

실제로 latent space의 직교 분해에서 시작하여 생성된 이미지에 인지할 수 있는 영향이 없는 일련의 낮은 크기의 방향을 식별한다. 이를 dormant라고 한다. 새 도메인을 추가하려면 용도를 변경할 dormant 방향을 선택한다. Base subspace라고 부르는 직교 subspace는 원래 도메인을 나타내기에 충분하다. Dormant 방향을 횡단하면 이제 원래 도메인과 새 도메인 사이의 전환이 발생하도록 dormant 방향의 용도를 변경하는 것을 목표로 한다. 특히, 전환은 원래 도메인의 변동 요인에서 분리되어야 한다. 이를 위해 base subspace을 선택한 dormant 방향을 따라 전송하여 용도 변경된 affine subspace을 정의한다. 용도가 변경된 subspace에서 샘플링된 latent code에서만 작동하도록 변환된 도메인 적응 방법을 적용하여 새 도메인을 캡처한다. 정규화 loss는 원래 도메인이 보존되도록 기본 subspace에 적용된다. Subspace가 평행하고 latent space가 풀려 있기 때문에 원래 도메인의 변동 요인은 암시적으로 보존된다. 여러 새 도메인의 경우 여러 dormant 방향에 걸쳐 이 절차를 반복하면 된다.

저자들은 본 논문의 방법을 StyleGAN과 Diffusion Autoencoder라는 두 가지 generator 아키텍처에 적용하고 여러 데이터셋에 대해 학습하고 수백 가지의 새로운 변동 요소로 generator를 확장한다. 확장된 모델은 원본 도메인과 새 도메인 모두에서 전문화된 도메인별 generator에 필적하는 고품질 이미지를 동시에 생성한다. 따라서 하나의 확장된 generator가 수백 개의 적응된 generator를 대체하여 실제 애플리케이션을 위한 생성 모델의 배포를 용이하게 한다. 또한 새로운 도메인은 기존 도메인과 함께 글로벌하고 disentangle된 변동 요인으로 학습된다. 이를 통해 생성 프로세스를 세밀하게 제어할 수 있고 새로운 애플리케이션과 능력을 사용할 수 있다.

Method

Latent code $z \in \mathcal{Z} \subseteq \mathbb{R}^D$에서 소스 도메인 \(\mathcal{D}_\textrm{src}\)의 이미지로 매핑하는 사전 학습된 generator $G_\textrm{src}$와 각각 loss function \(L_i, i \in \{1, \ldots, N\}\)로 정의되는 $N$개의 도메인 적응 task 집합으로 시작한다. 도메인 적응에서 $G_\textrm{src}$를 fine-tuning하여 $L_i$를 최소화하면 새 도메인 \(\mathcal{D}_i\)에서 이미지를 생성하는 generator $G_i$가 생성된다. 대조적으로, 본 논문의 목표는 원래 도메인 \(\mathcal{D}_\textrm{src}\)와 함께 모든 새로운 도메인 \(\cup_{i=1}^N \mathcal{D}_i\)를 동시에 모델링할 수 있는 단일 확장 generator $G^{+}$를 학습하는 것을 목표로 하는 도메인 확장이다. 새로운 도메인 $D_i$가 서로 disentangle된 그대로 남아 있는 소스 도메인의 변동 요소를 공유하도록 보장하고자 한다.

본 논문의 솔루션은 latent space를 각각의 새로운 도메인에 대해 하나씩 분리된 subspace로 분할하고 각 도메인 적응의 효과를 해당 subspace로 제한하는 것이다. 이를 위해 latent space에 도메인 확장을 지원하는 명시적 구조를 부여하고 새 도메인을 위해 예약된 특정 subspace의 latent만 사용하여 각 도메인 적응 loss를 최적화한다. 이 분해는 소스 generator의 동작을 유지하기 위해 정규화 목적 함수를 부과하는 원래 도메인 \(\mathcal{D}_\textrm{src}\)에 대한 base subspace를 예약한다. 아래 그림은 도메인 확장 알고리즘의 개요를 제공한다.

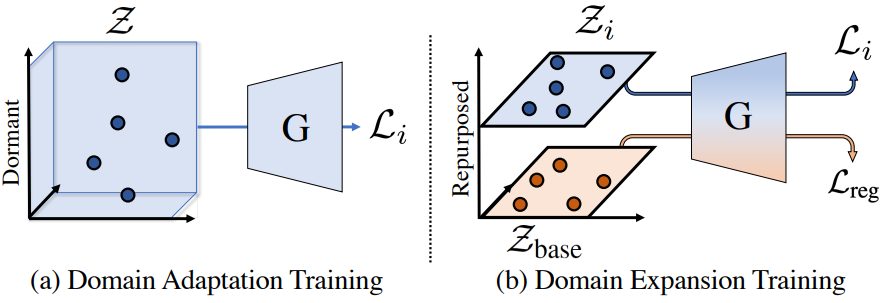
1. Structuring the Latent Space for Expansion

최신 생성 모델은 unsupervised 방식으로 선형 latent 방향을 따라 변동 요인을 나타내는 방법을 편리하게 학습한다. 적응 task에 의해 정의된 효과가 단일 선형 방향을 따라 표현되도록 latent space를 구조화하여 이 모델을 명시적으로 확장한다. $G^{+} (z)$, $G^{+} (z + sv_i)$에서 생성된 이미지가 소스 generator $G_\textrm{src} (z)$와 적응된 generator $G_i (z)$에서 해당 이미지로 서로 관련되는 일부 스칼라 $s$와 latent 방향 $v_i$가 존재해야 한다.

구체적으로 SeFA에 따라 latent space $\mathcal{Z}$에 작용하는 첫 번째 generator 레이어의 right singular vector로부터 latent space의 semantic orthogonal basis $V$를 얻는다. 저자들은 basis vector의 상대적으로 작은 subspace가 대부분의 generator $G_\textrm{src}$의 가변성을 나타내기에 충분하다는 것을 관찰했다. 다른 basis vector는 생성된 이미지에 거의 인지할 수 있는 영향을 미치지 않는다. SeFA에서도 마찬가지이다. 인지할 수 있는 효과가 없는 벡터를 dormant라고 한다.

Dormant 방향은 모델의 생성 능력에 영향을 미치지 않으므로 새로운 원하는 동작으로 용도를 변경할 수 있다. 따라서 dormant 방향으로만 분리된 영역에서 도메인 \(\mathcal{D}_\textrm{src}\)와 \(\mathcal{D}_i\)를 나타내도록 선택한다.

$N$개의 적응 task 각각에 대해 용도가 변경될 단일 dormant 방향 $v_i$를 할당한다. 나머지 방향 \(\{v_{N+1}, \ldots, v_D\}\)는 그대로 유지된다. 마지막으로 base subspace라고 하는 $\mathcal{Z}$의 subspace를 다음과 같이 정의한다.

\[\begin{equation} \mathcal{Z}_\textrm{base} = \textrm{span} (v_{N+1}, \ldots, v_D) + \bar{z} \end{equation}\]

여기서 $\bar{z}$는 generator를 학습시키는 데 사용되는 latent에 대한 분포의 평균이다. 그런 다음 용도가 변경된 각 방향 $v_i$에 대해 미리 정의된 스칼라 크기 $s$만큼 방향 $v_i$를 따라 이동되는 base subspace인 용도 변경된 subspace \(\mathcal{Z}_i\)를 정의한다.

\[\begin{equation} \mathcal{Z}_i = \mathcal{Z}_\textrm{base} + sv_i \end{equation}\]

아래에 설명할 도메인 확장 학습 절차는 subspace \(\mathcal{Z}_i\)가 목적 함수 $L_i$에 의해 영향을 받는 latent space의 유일한 부분이고 도메인 \(\mathcal{D}_i\)에서 이미지를 생성하도록 예약되어 있는지 확인한다. 직관적으로, $v_i$ 방향을 따라 base subspace를 이동하는 것은 두 가지를 달성하는 것을 목표로 한다.

1. \(\mathcal{Z}_\textrm{base}\)에서 상속된 변동 요인을 보존
2. 새로운 변동 요인을 단일 latent 방향 $v_i$로 제한

2. From Domain Adaptation to Expansion

새로운 도메인 \(\mathcal{D}_i\)에 대한 latent space $\mathcal{Z}$의 분리된 affine subspace \(\mathcal{Z}_i\)를 정의했으므로 이제 각 도메인 적응 목적 함수 $L_i$가 해당 subspace에만 영향을 미치도록 제한한다.

도메인 적응 목적 함수는 전체 space $\mathcal{Z}$에 정의된 분포 $p(z)$에서 샘플링된 latent code $z \in \mathcal{Z}$에서 생성된 이미지에 적용된다. 일반적으로 분포는 가우시안이거나 분포에서 가우시안에서 파생되지만 일부 예외가 존재한다. 본 논문의 전략은 이 표본 분포를 affine subspace \(\mathcal{Z}_i\)로 제한된 분포로 변환하는 것이다. 표준 orthogonal projection 연산자를 사용하여 $p(z)$의 샘플을 \(\mathcal{Z}_i\)에 project하여 수행한다.

\[\begin{equation} \textrm{proj}_{\mathcal{Z}_i} (z) = \sum_{j = N+1}^D (v_j^\top (z - \bar{z})) v_j + \bar{z} + sv_i \end{equation}\]

적응하려는 각각의 새로운 도메인에 대한 샘플링 분포를 $p_i$로 표시하면 모든 task에 대한 학습 loss는 다음과 같이 정의된다.

\[\begin{equation} \mathcal{L}_\textrm{expand} = \sum_{i=1}^N \mathbb{E}_{z \sim p_i (z)} \mathcal{L}_i (G (\textrm{proj}_{\mathcal{Z}_i} (z))) \end{equation}\]

3. Regularization

\(\mathcal{L}_\textrm{expand}\)를 최적화하면 단일 generator 내에서 새 도메인 \(\mathcal{D}_i\)에서 데이터를 생성하는 방법을 배울 수 있지만 불행히도 base subspace \(\mathcal{Z}_\textrm{base}\)가 제한되지 않은 상태로 남아 있으므로 학습 중에 변경되지 않은 상태로 유지된다는 보장이 없다. 실제로 $L_i$의 효과가 \(\mathcal{Z}_i\) 외부에서 “누출”되어 \(\mathcal{Z}_\textrm{base}\)에서 치명적인 망각을 일으키고 다른 subspace \(\mathcal{Z}_j\)에 바람직하지 않게 영향을 미치는 것을 관찰할 수 있다. 위 그림은 이러한 누출의 예를 보여준다.

이를 방지하기 위해 정규화를 통해 \(\mathcal{Z}_\textrm{base}\)에 대한 \(G_\textrm{src}\)의 동작 보존을 명시적으로 시행한다. 두 가지 성공적인 정규화 기술을 채택한다.

1. 망각을 완화하는 것으로 알려진 $L_\textrm{src}$에서 원래 학습된 loss로 generator를 계속 최적화한다.
2. Replay alignment를 적용한다. 이는 소스 generator의 고정된 복사본 출력과 생성기가 생성한 출력을 비교하는 재구성 loss이다. $L_2$ pixel loss와 LPIPS의 가중치 조합을 사용한다.

\[\begin{equation} \mathcal{L}_\textrm{recon} = \lambda_\textrm{lpips} \mathcal{L}_\textrm{lpips} (G_\textrm{src} (z), G(z)) + \lambda_{L_2} \| G_\textrm{src} (z) - G (z) \|_2 \end{equation}\]

여기서 \(\lambda_\textrm{lpips} = \lambda_{L_2} = 10\)은 가중치 hyperparameter이다. Replay alignment는 소스 도메인 \(\mathcal{D}_\textrm{src}\)를 보존할 뿐만 아니라 $G^{+}$를 소스 generator $G_\textrm{src}$에 정렬하는 추가 이점도 있다. 동일한 latent code $z$가 주어지면 유사한 출력을 생성한다는 의미이다.

결정적으로 base subspace \(\mathcal{Z}_\textrm{base}\)만 정규화한다. Subspace \(\mathcal{Z}_i\)가 새로운 동작을 학습하기 위해 변경되도록 허용되어야 하기 때문이다. 이를 위해 정규화 항을 계산하기 전에 latent code를 \(\mathcal{Z}_\textrm{base}\)에 project한다. 따라서 전반적인 정규화 목적 함수는 다음과 같다.

\[\begin{equation} \mathcal{L}_\textrm{reg} = \mathbb{E}_{z \sim p_\textrm{src} (z)} [\lambda_\textrm{src} \mathcal{L}_\textrm{src} (G (\textrm{proj}_{\mathcal{Z}_\textrm{base}} (z))) + \mathcal{L}_\textrm{recon} (G (\textrm{proj}_{\mathcal{Z}_\textrm{base}} (z)))] \end{equation}\]

여기서 \(\lambda_\textrm{src} = 1\)은 두 항의 균형을 이루고 $p_\textrm{src} (z)$는 $G_\textrm{src}$를 학습하는 데 사용되는 $\mathcal{Z}$에 대한 latent 분포이다. 따라서 최종 정규화된 도메인 확장 목적 함수는 다음과 같다.

\[\begin{equation} \mathcal{L}_\textrm{full} = \mathcal{L}_\textrm{expand} + \mathcal{L}_\textrm{reg} \end{equation}\]

Experiments

• Generator: StyleGAN2
• 도메인 적응 방법: StyleGAN-NADA, MyStyle
• 데이터셋: FFHQ, AFHQ Dog, LSUN Church, SD-Elephant

1. Evaluating Domains Individually

다음은 용도 변경된 방향에 따라 연속적으로 이미지를 변환한 결과이다.

다음은 도메인 적응 방법과 도메인 확장 방법의 성능을 정량적으로 비교한 표이다.

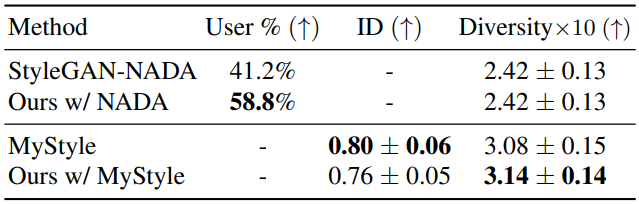
다음은 도메인 적응 방법과 도메인 확장 방법의 결과를 비교한 것이다.

2. Effect of Domains on Each Other

다음은 여러 도메인을 동시에 도입하는 효과를 조사한 것이다.

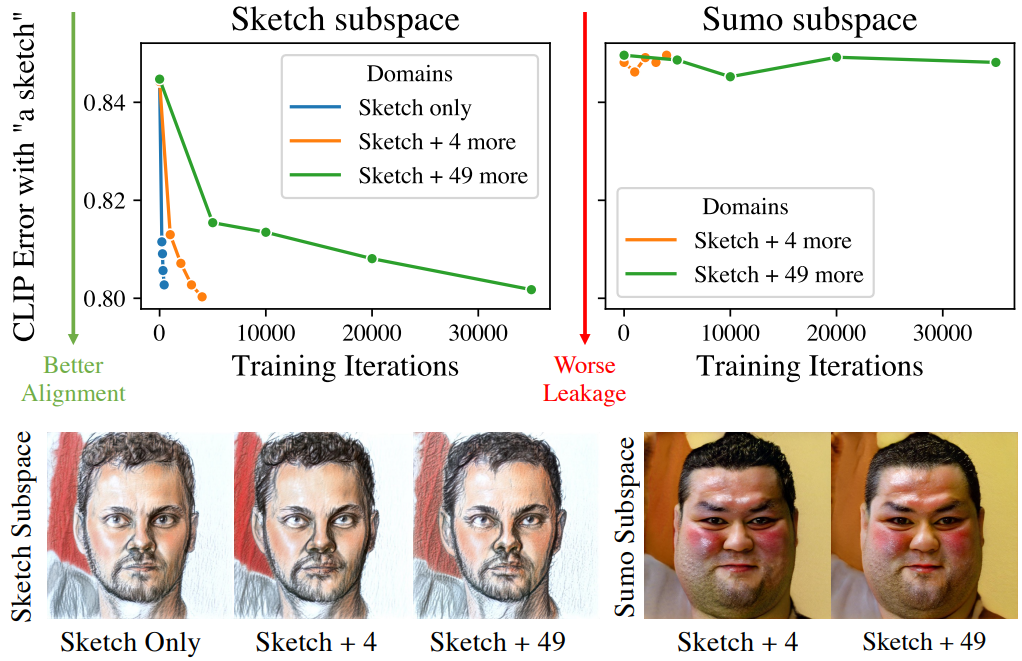
3. Compositionality

다음은 단순한 latent 탐색으로 여러 효과를 구성하는 예시이다.

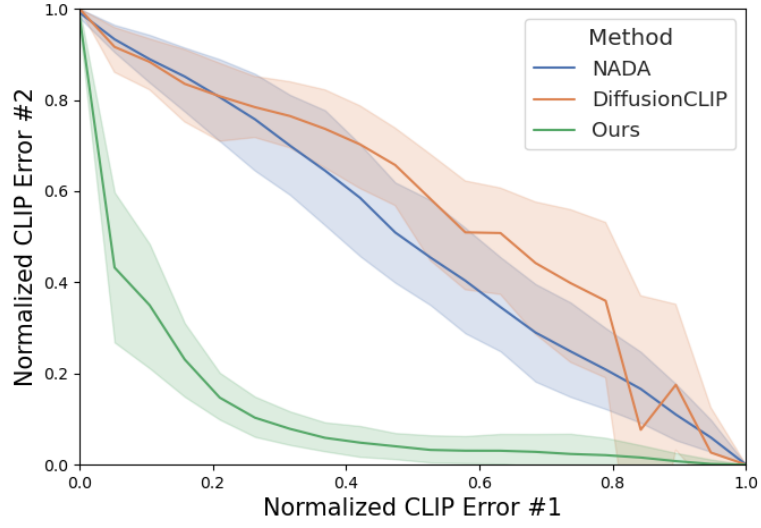
다음은 StyleGAN-NADA와 DiffusionCLIP에서 제안한 여러 도메인을 결합하는 방법과 본 논문의 generator의 합성성을 비교한 결과이다.

4. Preservation of the Source Domain

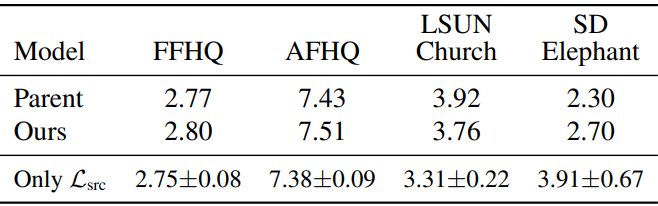
다음은 base subspace에서 이미지를 생성하고 소스 도메인 데이터셋에 대하여 FID를 측정한 표이다.

5. Generalization Beyond StyleGAN

다음은 Diffusion Autoencoder에 도메인 확장 방법을 적용한 결과이다.