[논문리뷰] DNGaussian: Optimizing Sparse-View 3D Gaussian Radiance Fields with Global-Local Depth Normalization
CVPR 2024. [Paper] [Page] [Github]
Jiahe Li, Jiawei Zhang, Xiao Bai, Jin Zheng, Xin Ning, Jun Zhou, Lin Gu
Beihang University | Chinese Academy of Sciences | Griffith University | RIKEN AIP | The University of Tokyo
11 Mar 2024

Introduction
Sparse한 입력을 사용한 novel view synthesis는 radiance fields에 대한 문제를 가지고 있다. NeRF의 최근 발전은 소수의 입력 뷰에서 사실적인 외관과 정확한 형상을 재구성하는 데 탁월했다. 그러나 대부분의 sparse-view NeRF는 낮은 처리 속도와 상당한 메모리 소비로 구현되므로 실제 적용을 제한하는 높은 시간과 계산 비용이 발생한다. 일부 방법은 그리드 기반 backbone을 사용하여 더 빠른 inference 속도를 달성하지만 종종 trade-off로 인해 높은 학습 비용이 발생하거나 렌더링 품질이 저하된다.

최근 3D Gaussian Splatting은 3D Gaussian을 사용하여 구조화되지 않은 3D Gaussian radiance field를 도입하여 dense한 입력 뷰에서 학습할 때 신속하고 고품질이며 저비용으로 novel view synthesis에서 놀라운 성공을 거두었다. Sparse한 입력만으로도 일부 명확하고 상세한 로컬 feature들을 재구성하는 놀라운 능력을 부분적으로 유지할 수 있다. 그럼에도 불구하고, 위 그림에서 볼 수 있듯이 뷰 제약 조건의 감소로 인해 장면 형상의 상당 부분이 잘못 학습되어 새로운 뷰 합성이 실패하게 된다. 본 논문은 이전의 깊이 정규화된 sparse-view NeRF의 성공에서 영감을 받아 사전 학습된 monocular depth estimator에서 얻은 깊이 정보를 사용하여 잘못 학습된 형상의 Gaussian을 수정하는 Depth Normalization Regularized Sparse-view 3D Gaussian Radiance Fields (DNGaussian)를 도입하여 few-shot novel view synthesis을 위한 더 높은 품질과 효율성을 추구하였다.
유사한 형태의 깊이 렌더링을 공유함에도 불구하고 3D Gaussian의 깊이 정규화는 NeRF에서 사용하는 것과 크게 다르다. 첫째, NeRF에 대한 기존 깊이 정규화 전략은 일반적으로 전체 모델을 정규화하기 위해 깊이를 사용한다. 이는 Gaussian에서 잠재적인 기하학적 충돌을 만들어 품질에 부정적인 영향을 미친다. 특히, 이 방법은 Gaussian의 모양을 복잡한 색상 표현이 아닌 부드러운 monocular depth에 맞추도록 강제하므로 디테일이 손실되고 모양이 흐릿해진다. 장면 형상의 기초가 Gaussian의 모양이 아닌 위치에 있다는 점을 고려하여, 저자들은 모양 파라미터를 고정하고 Gaussian 간의 움직임을 장려하여 공간적 reshaping을 가능하게 하는 Hard and Soft Depth Regularization를 제안하였다. 정규화 중에 형태를 변경하지 않고 Gaussian의 중심과 불투명도를 독립적으로 조정하기 위해 두 가지 유형의 깊이를 렌더링하여 복잡한 색상의 피팅과 부드럽고 대략적인 깊이 사이의 균형을 유지할 것을 제안하였다.
또한 Gaussian radiance field는 NeRF와 비교할 때 작은 깊이 오차에 더 민감하다. 이로 인해 Gaussian의 noisy한 분포를 만들고 복잡한 텍스처가 있는 영역에서 오차가 발생할 수 있다. 기존의 scale-invariant depth loss는 종종 depth map을 고정된 스케일로 정렬하는 것을 선택하여 작은 loss를 간과하게 된다. 이 문제를 해결하기 위해 저자들은 depth loss function에 Global-Local Depth Normalization을 도입하여 scale-invariant 방식으로 작은 로컬 깊이 변화를 학습하도록 장려하였다. DNGaussian은 로컬 및 글로벌 스케일 정규화를 통해 절대적인 스케일에 대한 지식을 유지하면서 작은 로컬 오차에 다시 초점을 맞추도록 loss function을 가이드하여 깊이 정규화를 위한 세부적인 형상 재구성 프로세스를 향상시켰다.
제안된 두 기술을 통합한 DNGaussian은 LLFF, Blender 및 DTU 데이터셋의 여러 sparse-view 설정에서 SOTA 방법에 비해 경쟁력 있는 품질과 뛰어난 디테일로 뷰를 합성한다. 이러한 이점은 상당히 낮은 메모리 비용, 학습 시간 25배 감소, 3000배 이상 빠른 렌더링 속도로 더욱 강화된다. 또한 DNGaussian은 복잡한 장면, 광범위한 뷰, 다양한 재료에 맞는 보편적인 능력을 보여주었다.
Method
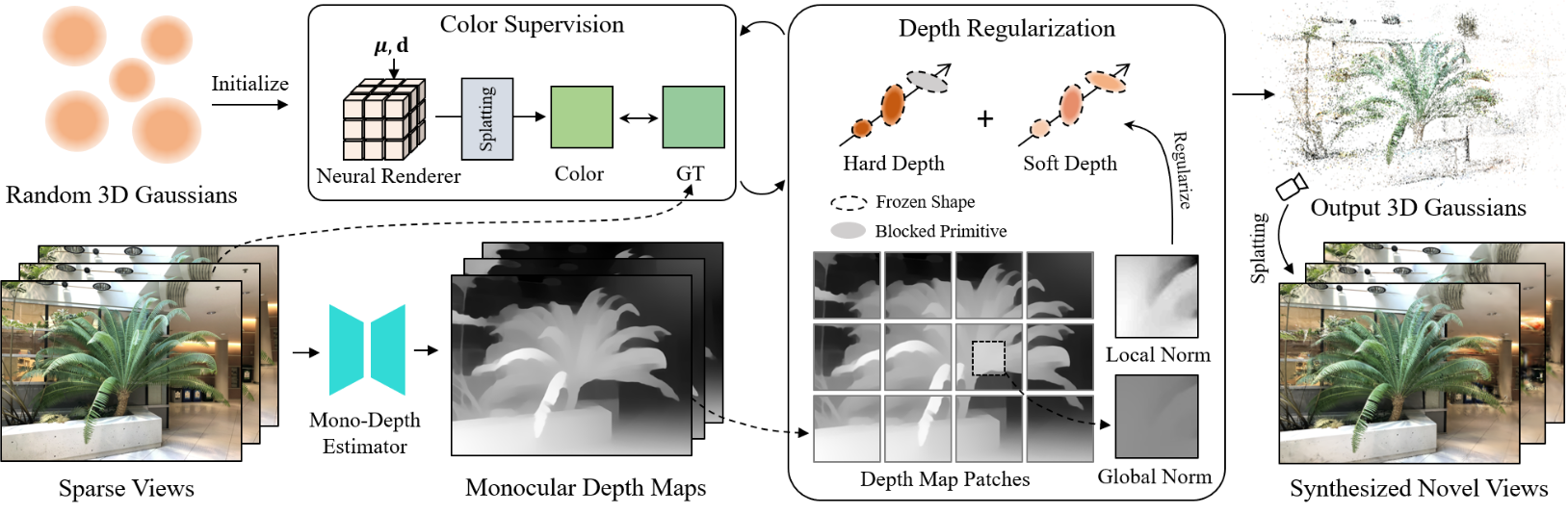
1. Depth Regularization for Gaussians
유사한 깊이 계산을 공유함에도 불구하고 NeRF에 대한 기존 깊이 정규화는 큰 차이로 인해 3D Gaussian로 전환할 수 없다. 먼저, 추가 파라미터에서 색상과 깊이 사이의 목표 충돌이 발생한다. 또한 연속적인 NeRF에 대한 이전 정규화는 밀도에만 초점을 맞추므로 discrete하고 유연한 Gaussian에서는 제대로 작동하지 않는다.
Shape Freezing
3D Gaussian은 NeRF보다 더 복잡한 깊이에 직접 영향을 미칠 수 있는 최적화 가능한 4개의 파라미터 \(\{\mu, s, q, \alpha\}\)를 가지고 있다. Monocular depth는 색상보다 훨씬 매끄럽고 피팅하기 쉽기 때문에 이전 sparse-view NeRF에서 널리 사용되는 전체 파라미터에 대한 깊이 정규화를 전체 모델에 적용하면 모양 파라미터가 목표 depth map에 overfitting된며 흐릿한 결과를 유발한다. 따라서 이러한 파라미터는 다르게 처리되어야 한다. 장면 형상은 주로 Gaussian의 위치 분포로 표현되므로 중심 $\mu$와 불투명도 $\alpha$를 정규화할 가장 중요한 파라미터로 간주할 수 있다. 왜냐하면 이 두 변수는 위치 자체와 위치 점유를 별도로 나타내기 때문이다. 또한 색상 재구성에 대한 부정적인 영향을 줄이기 위해 깊이 정규화에서 scaling $s$와 rotation $q$를 고정한다.
Hard Depth Regularization
본 논문은 Gaussian field의 공간적 reshaping을 달성하기 위해 먼저 가장 가까운 Gaussian의 이동을 장려하는 Hard Depth Regularization을 제안하였다. 가장 가까운 Gaussian은 표면을 구성할 것으로 예상되지만 종종 노이즈와 아티팩트를 유발한다. 예측된 깊이가 여러 Gaussian의 혼합으로 렌더링되고 누적 곱 $\tilde{\alpha}$로 다시 가중치가 부여된다는 점을 고려하여 모든 Gaussian에 큰 불투명도 값 $\tau$를 수동으로 적용한다. 그런 다음 카메라 중심 $o$와 픽셀 $x_p$를 가로지르는 광선의 가장 가까운 Gaussian으로 주로 구성된 “hard depth”를 렌더링한다.
\[\begin{equation} \mathcal{D}_\textrm{hard} = \sum_{i \in N} \tau (1 - \tau)^{i-1} \mathcal{G}_i^\textrm{proj} (x_p) \| \mu_i - o \|_2 \end{equation}\]이제 중심 $\mu$만 최적화되었으므로 잘못된 위치의 Gaussian은 불투명도를 낮추거나 모양을 변경하여 정규화되는 것을 피할 수 없으며 따라서 중심 $\mu$가 이동한다. 정규화는 monocular depth $\tilde{D}$에 가까운 hard depth \(\mathcal{D}_\textrm{hard}\)를 장려하기 위해 대상 이미지 영역 $\mathcal{P}$에서 similarity loss에 의해 구현된다.
\[\begin{equation} \mathcal{R}_\textrm{hard} (\mathcal{P}) = \mathcal{L}_\textrm{similar} (\mathcal{D}_\textrm{hard} (\mathcal{P}), \tilde{\mathcal{D}} (\mathcal{P})) \end{equation}\]Soft Depth Regularization
불투명도 최적화가 없기 때문에 hard depth에 대한 정규화만으로는 충분하지 않다. 또한 실제 렌더링된 “soft depth”의 정확성을 보장해야 한다. 그렇지 않으면 표면이 반투명해져서 빈 공간이 생길 수 있다. 이러한 관점에서 저자들은 중심 이동으로 인한 부정적인 영향을 피하기 위해 추가로 Gaussian 중심 $\tilde{\mu}$를 고정하고 불투명도 $\alpha$ 조정을 위해 Soft Depth Regularization을 제안하였다.
\[\begin{equation} \mathcal{D}_\textrm{soft} (x_p) = \sum_{i \in N} \| \mu_i - o \|_2 \times \tilde{\alpha}_i \prod_{j=1}^{i-1} (1 - \tilde{\alpha}_j) \\ \mathcal{R}_\textrm{soft} (\mathcal{P}) = \mathcal{L}_\textrm{similar} (\mathcal{D}_\textrm{soft} (\mathcal{P}), \tilde{\mathcal{D}} (\mathcal{P})) \end{equation}\]Hard 및 Soft Depth Regularization를 모두 사용하여 가장 가까운 Gaussian이 불투명도가 높은 적절한 위치에 머물도록 제한하여 완전한 표면을 구성한다.
2. Global-Local Depth Normalization

이전의 depth-supervised neural field는 일반적으로 depth map의 소스 스케일에 depth loss를 구축하였다. 이러한 유형의 정렬은 넓은 지역의 통계를 기반으로 고정된 스케일을 통해 모든 loss를 측정한다. 결과적으로, 특히 색상 재구성이나 광범위한 심도 변화와 같은 다중 목표를 처리할 때 작은 오차를 간과하게 될 수 있다. 이러한 간과는 이전 NeRF 기반 연구들에서는 그다지 중요하지 않을 수 있지만 Gaussian field에서는 더 큰 문제를 일으킬 수 있다.
Gaussian field에서 작은 깊이 오차를 수정하는 것은 작은 learning rate에서의 Gaussian의 움직임에 주로 의존하기 때문에 더 어렵다. 또한 깊이 정규화 중에 Gaussian의 위치가 수정되지 않으면 floater가 되어 오차가 발생할 수 있으며, 특히 위 그림과 같이 Gaussian이 모여 있는 세부적인 모양의 영역에서는 더욱 그렇다.
Local Depth Normalization
저자들은 이 문제를 해결하기 위해 패치별 로컬 정규화를 도입하여 loss function이 작은 오차에 다시 초점을 맞추도록 하였다. 구체적으로, 전체 depth map을 작은 패치로 자르고 평균값이 0이고 표준편차가 1에 가까운 예측 깊이와 monocular depth의 패치 $\mathcal{P}$를 정규화한다.
\[\begin{equation} \mathcal{D}^\textrm{LN} (x) = \frac{\mathcal{D} (x) - \textrm{mean} (\mathcal{D} (\mathcal{P}))}{\textrm{std} (\mathcal{D} (\mathcal{P})) + \epsilon}, \quad \textrm{s.t. } \; x \in \mathcal{P} \end{equation}\]여기서 $\epsilon$는 수치적 안정성을 위한 값이다. 이렇게 하면 모든 패치는 로컬 스케일로 정규화되며 loss는 내부에서 계산될 수 있다. 나중에 형상 재구성을 돕기 위해 Hard 및 Soft Depth Regularization에 로컬 깊이 정규화를 적용한다.
Global Depth Normalization
작은 로컬 loss들에 초점을 맞추는 것과는 대조적으로 전체적인 형태를 배우기 위해서는 글로벌한 뷰도 필요하다. 글로벌 스케일의 부족을 채우기 위해 깊이 정규화에 글로벌 깊이 정규화를 추가한다. 이를 통해 depth loss는 로컬 관련성을 유지하면서 글로벌 스케일을 인식하게 된다. 로컬 깊이 정규화와 유사하게 패치별 정규화를 적용하여 소스 스케일에서 깊이를 자유롭게 하고 로컬한 변경 사항에 집중한다. 유일한 차이점은 이미지 $\mathcal{I}$의 전체 이미지 깊이 \(\mathcal{D}_\mathcal{I}\)의 글로벌 표준 편차를 사용하여 패치의 깊이를 대체한다는 것이다.
\[\begin{equation} \mathcal{D}^\textrm{LN} (x) = \frac{\mathcal{D} (x) - \textrm{mean} (\mathcal{D} (\mathcal{P}))}{\textrm{std} (\mathcal{D}_\mathcal{I})}, \quad \textrm{s.t. } \; x \in \mathcal{P}, \; \mathcal{P} \subseteq \mathcal{I} \end{equation}\]또한 패치별 정규화는 depth rank distillation과 유사한 효과를 제공하는 로컬 상대 깊이 학습을 통해 monocular depth의 장거리 오차를 피할 수도 있다. 그러나 다른 점은 형상 reshaping을 위해 모델이 절대적인 깊이 변화를 무시하기보다는 학습하도록 권장한다는 것이다.
3. Training Details
Loss Function
Loss function은 color reconstruction loss \(\mathcal{L}_\textrm{color}\), hard depth regularization \(\mathcal{R}_\textrm{hard}\), soft depth regularization \(\mathcal{R}_\textrm{soft}\)의 세 부분으로 구성된다. 3D Gaussian Splatting을 따라 \(\mathcal{L}_\textrm{color}\)는 렌더링된 이미지 $\hat{\mathcal{I}}$와 ground-truth $\mathcal{I}$에 대한 L1 loss와 D-SSIM 항의 조합이다.
\[\begin{equation} \mathcal{L}_\textrm{color} = \mathcal{L}_1 (\hat{\mathcal{I}}, \mathcal{I}) + \lambda \mathcal{L}_\textrm{D-SSIM} (\hat{\mathcal{I}}, \mathcal{I}) \end{equation}\]깊이 정규화 \(\mathcal{R}_\textrm{hard}\)와 \(\mathcal{R}_\textrm{soft}\)는 모두 로컬 항과 글로벌 항을 포함하며, 유사도를 측정하기 위해 L2 loss를 사용한다. 두 정규화는 다음과 같다.
\[\begin{aligned} \mathcal{R}_\textrm{hard} &= \mathcal{L}_2 (\mathcal{D}_\textrm{hard}^\textrm{GN}, \tilde{\mathcal{D}}^\textrm{GN}) + \gamma \mathcal{L}_2 (\mathcal{D}_\textrm{hard}^\textrm{LN}, \tilde{\mathcal{D}}^\textrm{LN}) \\ \mathcal{R}_\textrm{soft} &= \mathcal{L}_2 (\mathcal{D}_\textrm{soft}^\textrm{GN}, \tilde{\mathcal{D}}^\textrm{GN}) + \gamma \mathcal{L}_2 (\mathcal{D}_\textrm{soft}^\textrm{LN}, \tilde{\mathcal{D}}^\textrm{LN}) \end{aligned}\]실제로는 제약 조건을 완화하기 위해 L2 loss에 대한 error tolerance를 사용한다. 전체 loss function은 다음과 같다.
\[\begin{equation} \mathcal{L} = \mathcal{L}_\textrm{color} + \mathcal{R}_\textrm{hard} + \mathcal{R}_\textrm{soft} \end{equation}\]Neural Color Renderer
3D Gaussian Splatting은 spherical harmonics를 통해 색상을 저장하지만, sparse한 입력 뷰만 사용하면 overfitting되기 쉽다. 이 문제를 해결하기 위해 그리드 인코더와 MLP를 Neural Color Renderer로 사용하여 각 Gaussian의 색상을 예측한다. inference 중에 중앙값 결과를 저장하고 가속을 위해 뷰 방향을 병합하기 위한 마지막 MLP 레이어만 계산한다.
Experiments
- 데이터셋
- NeRF Blender Synthetic dataset (Blender): 8개의 뷰에서 학습, 25개의 뷰에서 테스트
- DTU, LLFF: 3개의 뷰에서 학습, 나머지 이미지에서 테스트
- 구현 디테일
- 총 6,000 iteration으로 학습
- 안정성을 위해 1,000 iteration 이후부터 Soft Depth Regularization을 적용
- $\gamma = 0.1$, $\tau = 0.95$
- Neural renderer
- hash encoder level = 16
- 해상도 범위: 16 ~ 512
- 최대 크기: $2^{19}$
- MLP: 5 layer, 64 hidden dim
- Monocular depth estimator: DPT
1. Comparison
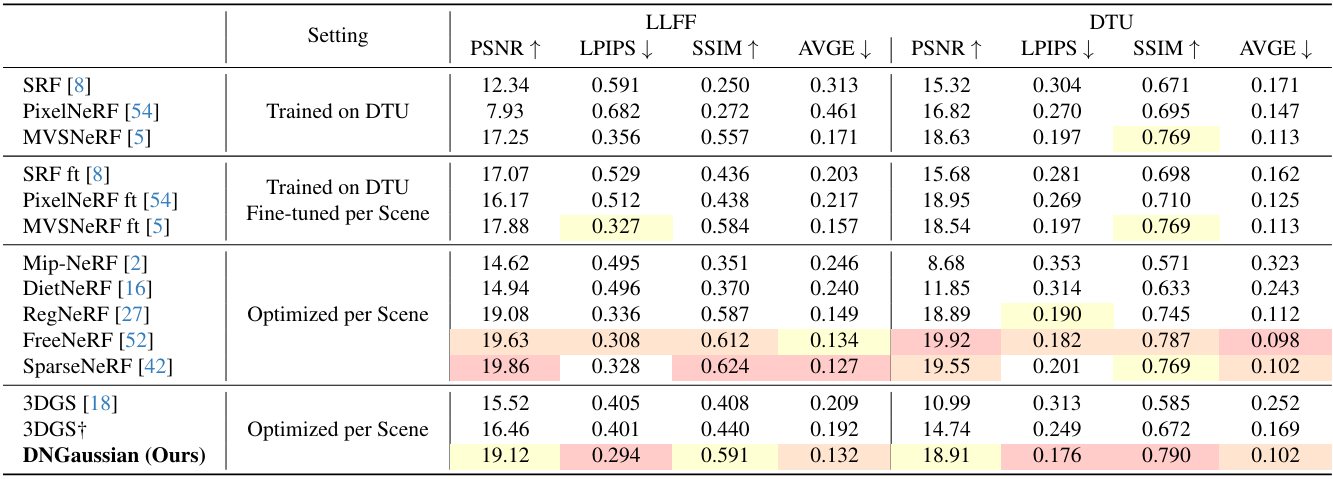
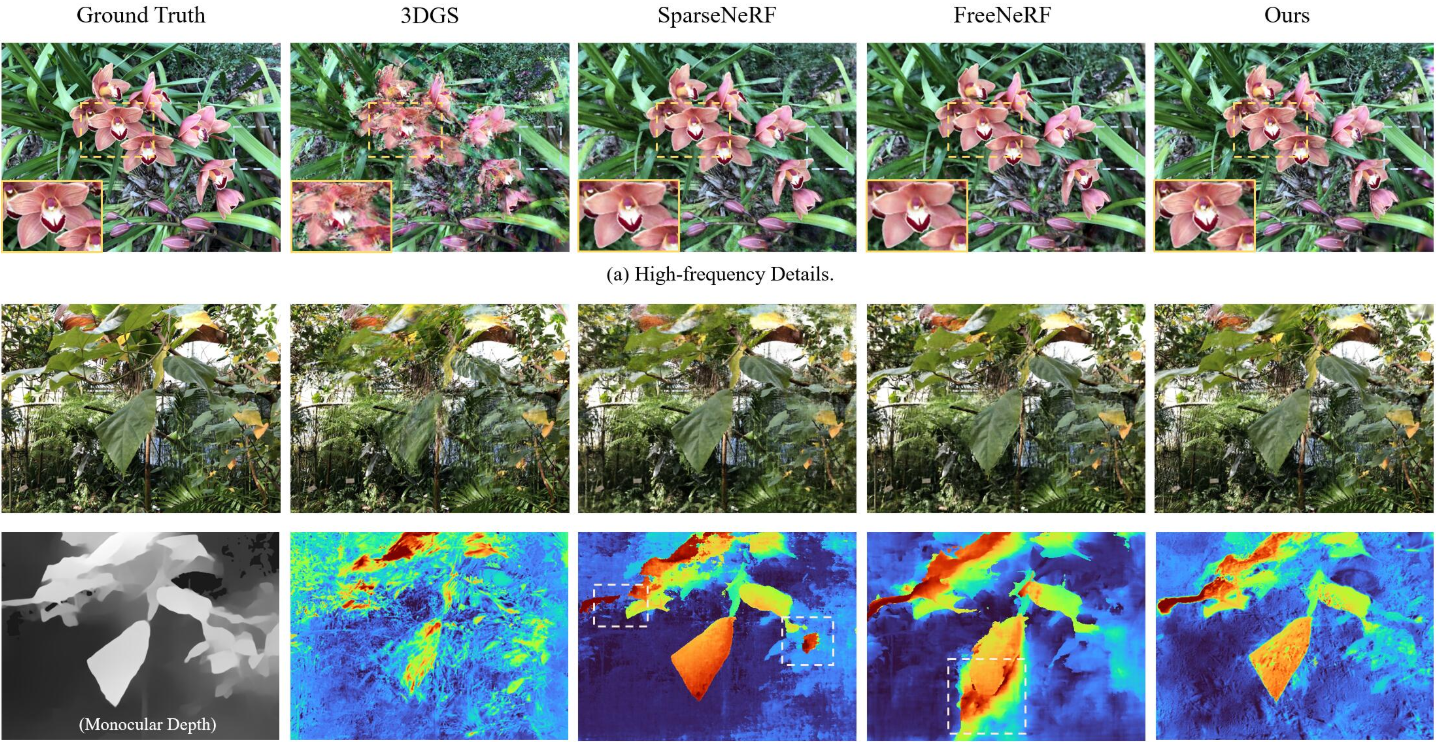
다음은 다른 방법들과 LLFF 및 DTU에서 비교한 결과이다.

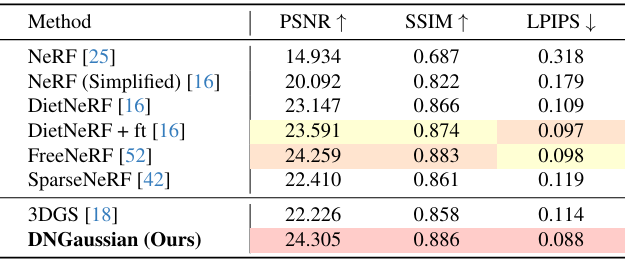
다음은 다른 방법들과 Blender에서 비교한 결과이다.

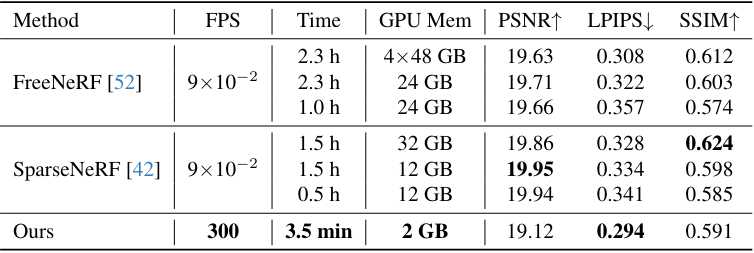
다음은 효율성을 비교한 표이다.
2. Ablation Study
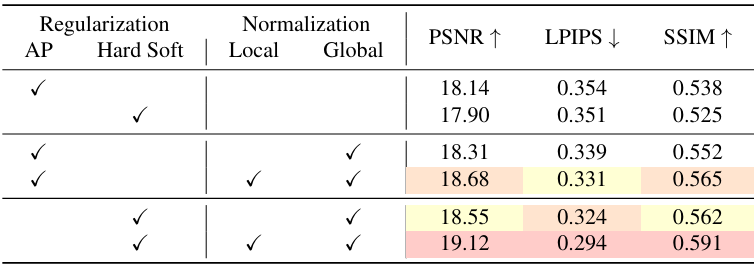
다음은 ablation study 결과이다.

다음은 파라미터 고정에 대한 ablation study 결과이다.

