[논문리뷰] DNF-Intrinsic: Deterministic Noise-Free Diffusion for Indoor Inverse Rendering
ICCV 2025. [Paper] [Page] [Github]
Rongjia Zheng, Qing Zhang, Chengjiang Long, Wei-Shi Zheng
Sun Yat-sen University | Meta Reality Labs
5 Jul 2025
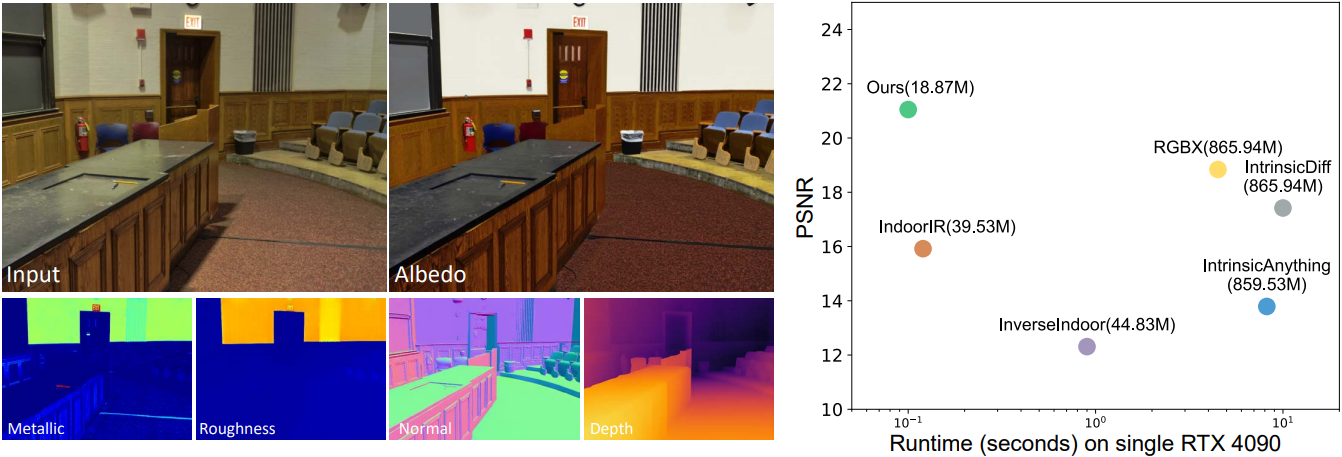
Introduction
최근 사전 학습된 diffusion model 모델의 강력한 이미지 prior를 활용하여 noise-to-intrinsic 방식으로 deterministic하지 않은 inverse rendering을 달성하는 방법들이 주목을 받고 있다. 이 패러다임에 따라 일부 방법은 합성 데이터를 사용하여 사전 학습된 diffusion model을 fine-tuning하여 inverse rendering을 해결하는 것을 제안하였다. 그러나 기본적으로 다음 세 가지 한계가 있다.
- 일반적으로 랜덤 noise를 intrinsic에 매핑하기 위해 많은 수의 denoising step이 필요하기 때문에 inference 속도가 일반적으로 느리다.
- Noise-to-intrinsic 패러다임을 사용하면 intrinsic 예측을 위해 완전한 이미지 구조와 외형 정보를 활용할 수 없기 때문에 고품질 결과를 robust하게 생성할 수 없다.
- 예측된 intrinsic에서 이미지를 재구성하는 데 대한 명시적 제약이 없기 때문에 물리적으로 설득력 있는 inverse rendering을 달성하지 못할 수 있다.
이러한 한계를 해결하기 위해, 본 논문에서는 실내 장면의 robust하고 효율적이며 물리적으로 설득력 있는 diffusion 기반 inverse rendering 방식인 DNF-Intrinsic을 제시하였다. 기존 방식처럼 이미지 조건부 noise-to-intrinsic 매핑을 학습하는 대신, 본 논문에서는 Gaussian noise 대신 원본 이미지를 입력으로 사용하여 flow matching을 통해 deterministic한 방식으로 intrinsic을 예측하는 image-to-intrinsic 매핑을 제안하였다. 이를 통해 원본 이미지의 비전 정보를 최대한 활용하여 더 나은 intrinsic 예측 성능을 얻을 수 있을 뿐만 아니라, 많은 denoising step에서 발생하는 높은 계산 비용을 피할 수 있다. Generative renderer는 예측된 intrinsic으로부터 원본 이미지를 재구성할 수 있도록 명시적으로 제한함으로써 물리적으로 의미 있는 inverse rendering을 달성하도록 추가로 설계되었다.
Method
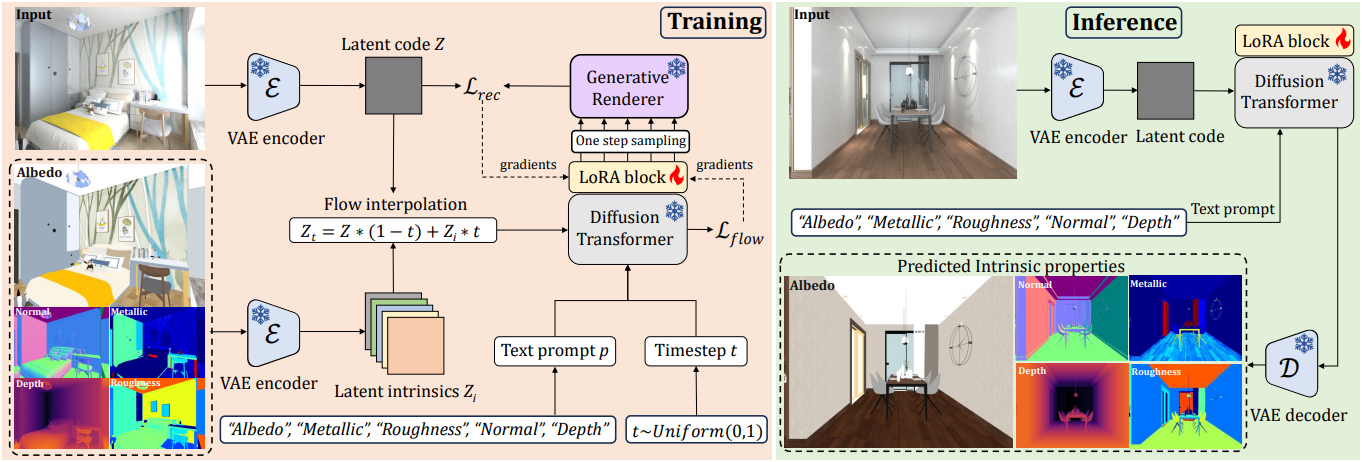
본 논문의 목표는 단일 RGB 실내 이미지가 주어졌을 때 사전 학습된 diffusion model로부터 fine-tuning된 단일 모델을 통해 albedo, metallic, roughness, normal, depth를 복구하는 것이다.
1. Problem Formulation
Text-to-image 생성과 달리 inverse rendering은 deterministic한 image-to-image task이다. 강력한 diffusionp prior를 활용하기 위해, 대부분의 기존 diffusion 기반 inverse rendering 방법은 입력 이미지를 조건으로 하는 noise-to-intrinsic diffusion 문제로 task를 정의하는 text-to-image 방법을 따른다.
Albedo 추정을 예로 들면, 사전 학습된 diffusion model은 일반적으로 albedo $A \sim \mathbb{R}^{W \times H \times 3}$에 대한 조건부 분포 $D(A \vert I)$를 배우도록 학습된다. 여기서 조건 $I \sim \mathbb{R}^{W \times H \times 3}$은 입력 이미지이다. Diffusion model \(\epsilon_\theta\)의 학습 objective는 다음과 같다.
\[\begin{equation} x_t = \sqrt{\vphantom{1} \bar{\alpha}_t} A + \sqrt{1 - \bar{\alpha}_t} \epsilon, \quad t \in \{0, 1, \ldots, T\} \\ \mathcal{L} = \mathbb{E}_{t, A, \epsilon} \| \epsilon_\theta (x_t, t, I) - \epsilon \|_2^2 \end{equation}\](\(\bar{\alpha}_t\)는 noise schedule, $x_t$는 timestep $t$에서 noise가 적용된 이미지, $\epsilon \sim \mathcal{N}(0,I)$는 Gaussian noise)
Denoising process는 $x_t$의 noise를 점진적으로 제거하여 $x_{t−1}$을 얻는다.
\[\begin{equation} d(x_t) = \sqrt{1 - \bar{\alpha}_{t-1}} - \tau^2 \epsilon_\theta \\ x_{t-1} = \sqrt{\vphantom{1} \bar{\alpha}_{t-1}} (\frac{x_t - \sqrt{1 - \bar{\alpha}_t} \epsilon_\theta}{\sqrt{\vphantom{1} \bar{\alpha}_t}}) + d(x_t) + \tau \epsilon \end{equation}\]($\tau$는 주입되는 noise의 양을 제어하는 파라미터)
Inference 과정에서는 순수한 Gaussian noise 이미지 $x_T$로 시작하여 denoising process를 통해 \(t \in \{T, \ldots, 0\}\)에서 noise를 점진적으로 제거하여 최종적으로 깨끗한 albedo 예측을 도출한다.
앞서 언급한 이미지로 컨디셔닝된 noise-to-intrinsic 패러다임이 material 및 geometry 추정에 유망한 결과를 보여주었지만 여전히 해결해야 할 몇 가지 문제가 있다.
- 이 패러다임은 구조와 외형이 저하된 noise가 있는 이미지에서 작동하는 방법을 학습하는데, 이는 구조 및 외형 정보가 inverse rendering에 중요한 것으로 알려져 있기 때문에 필연적으로 전체 성능에 해를 끼친다.
- Noise를 target에 매핑하는 본질적인 어려움과 곡선 샘플링 궤적 때문에 대부분 inference 속도가 낮다.
- 예측된 intrinsic이 입력 이미지를 재구성할 수 있다는 것을 명시적으로 적용하지 않고 학습하기 때문에 물리적으로 그럴듯한 고품질 intrinsic을 생성하는 데 어려움을 겪는다.
위와 같은 문제가 존재하기 때문에, 저자들은 소스 이미지를 입력으로 사용하여 image-to-intrinsic 매핑을 학습시키고, 재구성이 제한된 고품질 intrinsic을 deterministic하고 보다 효율적인 방식으로 예측하는 diffusion 기반 inverse rendering 방법을 개발하고자 하였다.
2. Deterministic Image-to-Intrinsic Diffusion
더욱 robust하고 효율적인 inverse rendering을 가능하게 하기 위해, 기존 방식처럼 DDPM 기반 이미지 조건부 noise-to-intrinsic 매핑 대신, flow matching을 통해 deterministic한 image-to-intrinsic 매핑을 학습하는 것을 제안하였다. 구체적으로, ODE 모델을 사용하여 입력 이미지 \(Z \sim \pi_I\)의 latent code를 짧고 직선적인 궤적을 통해 타겟 latent intrinsic \(Z_p \sim \pi_p\)로 전달함으로써, 적은 샘플링 step만으로도 예측이 가능하다. 학습 과정에서 noise가 포함된 latent $Z_t$는 interpolation을 통해 구해진다.
\[\begin{equation} Z_t = (1-t) Z + t Z_p, \quad t \in [0, 1] \end{equation}\]그런 다음, 신경망 \(\mu_\theta\)를 사용하여 입력 이미지와 각 intrinsic 사이의 경로를 따라 flow velocity를 학습시킨다.
\[\begin{equation} \mathcal{L}_\textrm{single} = \mathbb{E}_{t, Z, Z_p} \| \mu_\theta (Z_t, t) - (Z_p - Z) \|_2^2 \end{equation}\]본 논문에서는 5가지 intrinsic을 공동으로 추정하는 inverse rendering을 달성하고자 하였다. 이를 위해 각 intrinsic의 텍스트 프롬프트를 트리거로 사용하여 아키텍처를 수정하지 않고도 여러 intrinsic을 예측하기 위한 하나의 사전 학습된 diffusion model을 적용한다. 구체적으로, inverse rendering을 동일한 latent code $Z$에서 시작하여 다양한 latent intrinsic $Z_i$를 향해 서로 다른 intrinsic 궤적을 따라 발산하는 deterministic한 일대다 분포 매핑 문제로 설정한다. 따라서 텍스트 프롬프트를 intrinsic 궤적의 방향을 제어하는 간단한 트리거로 사용한다. 학습 loss는 다음과 같이 정의된다.
\[\begin{equation} \mathcal{L}_\textrm{flow} = \mathbb{E}_{t, Z, Z_i} \sum_{i=1}^N \| \mu_\theta (Z_t, t, p_i) - (Z_i - Z) \|_2^2 \end{equation}\]($N$은 intrinsic 유형의 개수, \(p_i \in \{\textrm{"albedo"}, \textrm{"metallic"}, \textrm{"roughness"}, \textrm{"normal"}, \textrm{"depth"}\}\)는 대상 intrinsic을 나타내는 텍스트 트리거를 나타내고, $Z_i$는 해당 latent intrinsic)
Diffusion denoising에 주로 UNet을 사용하는 기존 방법과 달리, Diffusion Transformer (DiT)가 글로벌 정보 활용이 inverse rendering의 성공에 매우 중요하기 때문에 더 효과적인 flow 추정기이다. 따라서 저자들은 Stable Diffusion V3에서 사전 학습된 DiT를 flow estimator \(\mu_\theta\)로 fine-tuning했다. 사전 학습된 모델 전체를 fine-tuning하거나 ControlNet branch를 추가하는 대신, 사전 학습된 DiT의 원래 아키텍처를 유지하고 LoRA를 적용하여 매우 적은 수의 파라미터를 fine-tuning했다.
3. Generative Renderer
각 intrinsic은 학습 데이터셋의 해당 GT에 의해 학습되지만, 실제로 이러한 intrinsic과 입력 이미지 사이에는 직접적인 제약 조건이 없으므로 잠재적인 관계는 무시된다. 저자들은 이 문제를 해결하기 위해 generative renderer를 개발하고, 예측된 intrinsic으로부터 입력 이미지를 재구성할 수 있도록 재구성 loss를 설계하였다. 구체적으로, ControlNet을 사용하여 5가지 intrinsic을 Stable Diffusion의 사전 학습된 모델에 제어 신호로 통합하고, 이를 generative renderer $\mathcal{R}$로 fine-tuning하여 주어진 GT intrinsic을 기반으로 입력 이미지를 렌더링한다.
\[\begin{equation} x_t = \sqrt{\vphantom{1} \bar{\alpha}_t} Z + \sqrt{1 - \bar{\alpha}_t} \epsilon, \quad t \in \{0, 1, \ldots, T\} \\ \mathcal{L} = \mathbb{E}_{t, Z, \epsilon} \| \mathcal{R}_\theta (x_t, t, (A, M, R, N, D)) - \epsilon \|_2^2 \end{equation}\]($Z$는 입력 이미지의 latent code, $A$는 albedo, $M$은 metallic, $R$은 roughness, $N$은 normal, $D$는 depth)
장면 조명은 조건 입력으로 제공되지 않으므로, 렌더링 프로세스를 미지의 조명 조건을 나타내는 stochasticity를 intrinsic을 조건으로 하는 noise-to-image 매핑으로 모델링한다. 구체적으로, 사전 학습된 generative renderer $\mathcal{R}$을 사용하여 다음과 같은 재구성 loss를 정의한다.
\[\begin{equation} \mathcal{L}_\textrm{rec} = \mathbb{E}_{t, Z, \epsilon} \| \mathcal{R} (\sqrt{\vphantom{1} \bar{\alpha}_t} Z + \sqrt{1 - \bar{\alpha}_t} \epsilon_t, t, \mu_\theta (I)) - \epsilon \|_2^2 \end{equation}\](\(\mu_\theta (I) = (\tilde{A}, \tilde{M}, \tilde{R}, \tilde{N}, \tilde{D})\)는 5가지 intrinsic 모두에 대한 1-step 추정, \(\epsilon_t\)는 미지의 조명을 나타내는 샘플링된 noise)
DreamFusion에서 영감을 받은 \(\mathcal{L}_\textrm{rec}\)는 generative renderer $\mathcal{R}$을 통해 backpropagation하지 않고 \(\mu_\theta\)에 대한 gradient를 계산하기 위해 Score Distillation Sampling (SDS) loss로 구현된다. 구체적으로, \(\mathcal{L} = \mu_\theta (I) \cdot \textrm{stop-gradient} (\mathcal{L}_\textrm{rec})\)의 gradient를 계산한다. 그러면, optimizer를 사용하여 파라미터 $\theta$를 업데이트할 수 있다.
재구성 loss에서 조명 부족을 해결하기 위해, 학습 과정에서 다양한 조명을 샘플링한다. 이는 가능한 모든 조명을 통합하는 것과 동일하다. 따라서 재구성 loss를 최소화함으로써, 모델은 조명 효과를 제거하는 방향으로 학습되고, 최종적으로 조명에 독립적인 고유 속성으로 수렴한다.
4. Inference
Inference 시에 VAE 인코더 $\mathcal{E}$는 입력 이미지 $I$를 latent code $Z$로 인코딩한다. 그러면 intrinsic 궤적의 방향은 특정 텍스트 프롬프트 $p$에 의해 결정된다. 프롬프트 $p_i$를 사용하여 $Z_0 = Z$에서 시작하여, 다음과 같이 타겟 latent intrinsic을 향해 점진적으로 전환할 수 있다.
\[\begin{equation} Z_{t+\frac{1}{K}} = Z_t + \frac{1}{K} \mu_\theta (Z_t, t, p_i) \end{equation}\]($K = 10$은 총 샘플링 step 수, \(t = \{ 0, \ldots, K-1 \}/K\))
타겟 latent intrinsic을 얻은 후, VAE 디코더 $\mathcal{D}$를 사용하여 해당 intrinsic을 복구한다.
Experiments
1. Comparison with State-of-the-art Methods
다음은 합성 데이터셋인 InteriorVerse에서의 inverse rendering 결과를 비교한 것이다.
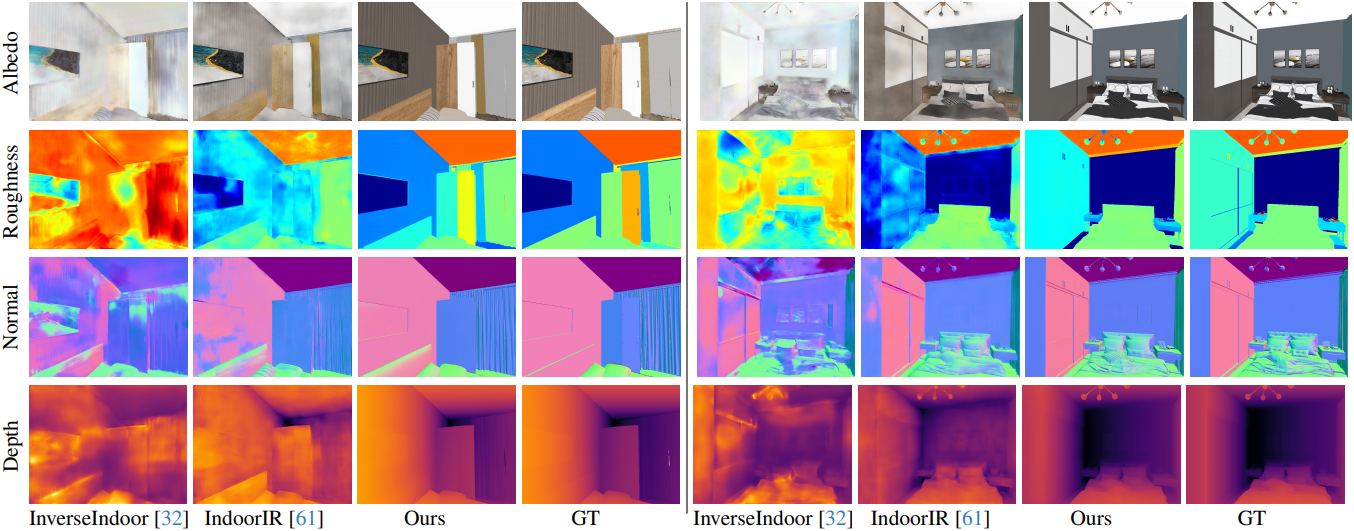
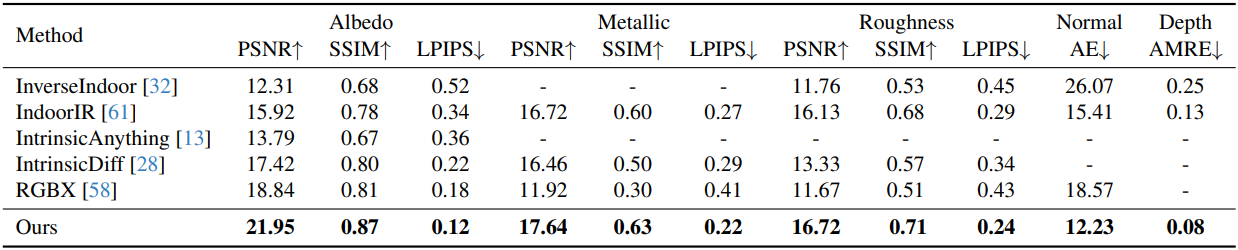
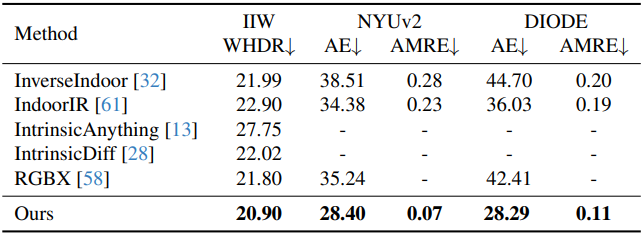
다음은 albedo 및 geometry 성능을 비교한 결과이다.
다음은 albedo 추정 결과를 비교한 것이다.

다음은 normal 추정 결과를 비교한 것이다.

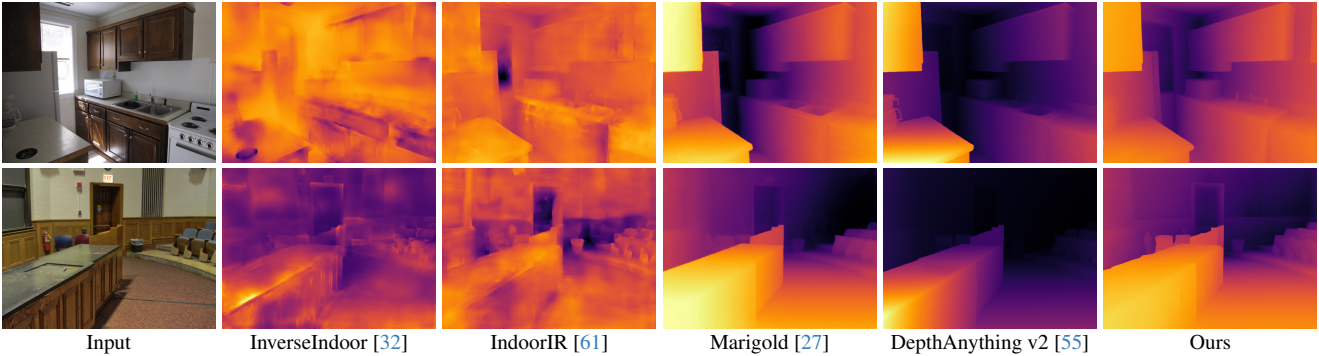
다음은 깊이 추정 결과를 비교한 것이다.
2. Ablation
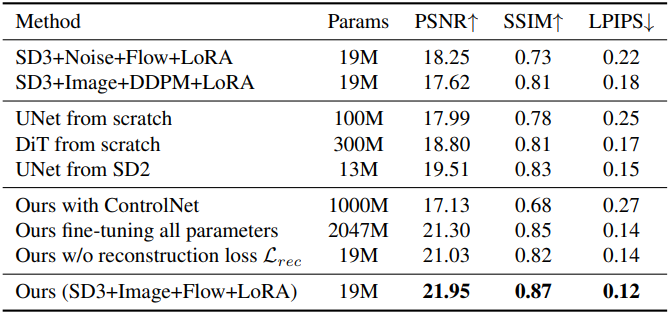
다음은 albedo 추정에 대한 ablation study 결과이다.

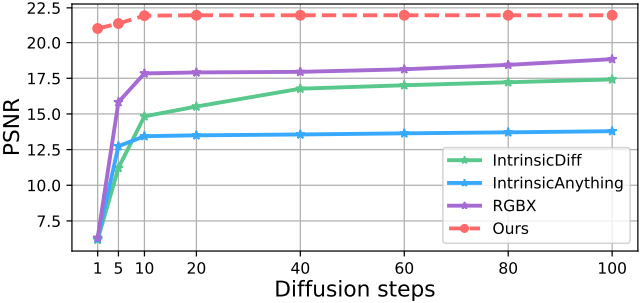
다음은 diffusion step에 따른 albedo 추정 성능을 비교한 그래프이다.
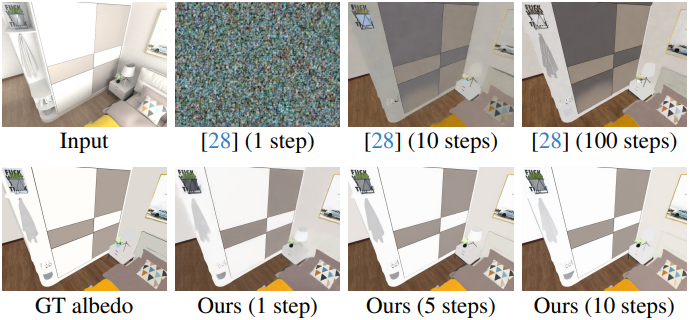
3. Application
다음은 다양한 응용 예시이다.
