[논문리뷰] DN-Splatter: Depth and Normal Priors for Gaussian Splatting and Meshing
WACV 2025. [Paper] [Page] [Github]
Matias Turkulainen, Xuqian Ren, Iaroslav Melekhov, Otto Seiskari, Esa Rahtu, Juho Kannala
ETH Zurich | Tampere University | Aalto University | Spectacular AI
26 Mar 2024
Introduction
3D Gaussian Splatting (3DGS)은 최적화 가능한 여러 미분 가능한 3D Gaussian들로 장면을 표현한다. 이 명시적인 표현을 통해 크고 복잡한 장면의 실시간 렌더링이 가능하다. 장면 모양과 형상이 Gaussian의 위치, 모양, 색상 속성으로 직접 표현되므로 상호 운용성이 더 높은 장면 표현을 제공한다. 그러나 최적화 중에 3D 및 표면 제약이 부족하여 아티팩트와 모호함이 발생할 가능성이 높다. 장면에는 수백만 개의 Gaussian이 포함되는 경우가 많으며 해당 속성들은 photometric loss들만을 직접 수정된다. 따라서 메쉬 표현으로 변환될 수 있는 시각적, 기하학적으로 더 부드럽고 더 그럴듯한 3D 재구성을 생성하는 더 나은 정규화 기술을 탐색하는 데 거의 초점이 맞춰지지 않았다.
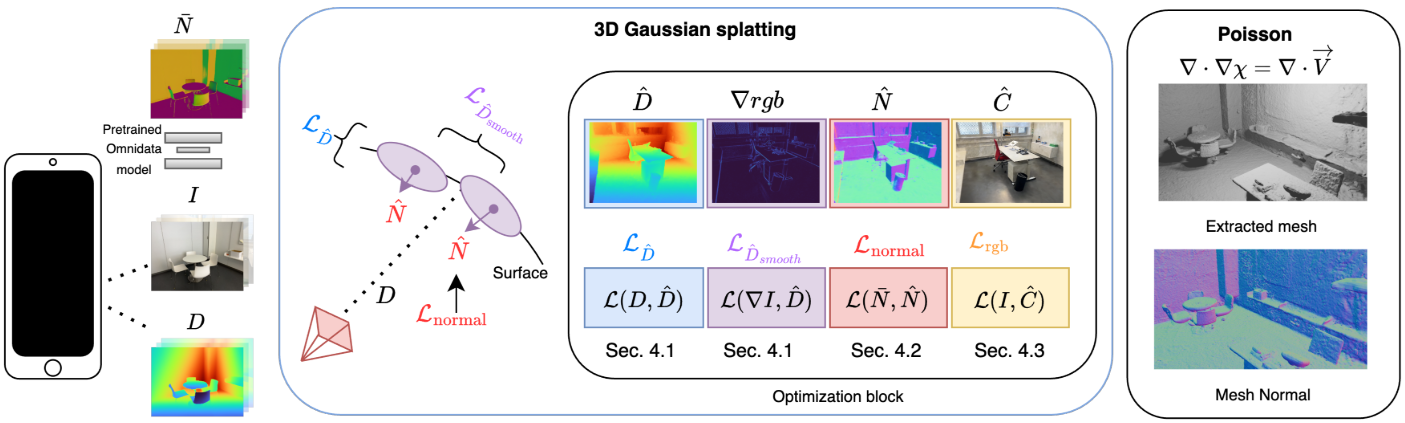
본 논문은 monocular depth 및 normal 추정 네트워크의 발전과 ToF 및 깊이 센서가 장착된 풍부한 모바일 장치로 얻은 geometric prior를 사용하여 3DGS의 정규화를 탐구하였다. 깊이와 smoothness 제약 조건을 사용하여 실내 장면에서 3DGS 최적화를 정규화하여 캡처된 장면 형상을 더 잘 존중하면서 렌더링 결과를 향상시킨다. Gaussian들로부터 normal을 추정하고 monocular normal prior에서 추정된 장면 형상을 기반으로 Gaussian들을 실제 표면 경계와 정렬한다. 이 간단한 정규화 전략을 사용하여 Gaussian 장면 표현에서 메쉬를 추출하여 더 부드럽고 기하학적으로 유효한 재구성을 생성한다.
Method
1. Leveraging Depth Cues
픽셀당 $z$-depth 추정치 $\hat{D}$는 색상 값과 유사하게 알파 블렌딩을 사용하여 렌더링된다.
\[\begin{equation} \hat{D} = \sum_{i \in \mathcal{N}} d_i \alpha_i \prod_{j=1}^{i-1} (1 - \alpha_j) \end{equation}\]여기서 $d_i$는 $i$번째 Gaussian의 $z$-depth 좌표이다. 3DGS는 광선을 따라 픽셀별로 Gaussian을 개별적으로 정렬하는 대신 효율성을 위해 view frustum의 전체 Gaussian들을 한 번에 정렬하기 때문에 $\hat{D}$는 픽셀당 깊이의 근사치일 뿐이다. 2D projection과 전체 정렬 후에는 특정 방향에 대한 $z$-depth 순서가 정확하다고 보장되지 않는다. 그러나 장면에 수백만 개의 Gaussian이 포함될 수 있으므로 각 픽셀을 깊이별로 정렬하는 것은 계산 비용이 너무 많이 든다. $\hat{D}$는 정확하지는 않지만 여전히 효과적이며, 특히 실내 데이터셋에서 일반적으로 볼 수 있는 보다 규칙적인 형상의 경우 더욱 그렇다.
Sensor depth
LiDAR 또는 센서로 측정한 깊이가 포함된 데이터셋의 depth map에 깊이 정규화를 직접 적용한다. 일반적인 상업용 깊이 센서는 물체 경계에 가장자리가 매끄럽지 않으며 매끄러운 표면에서 부정확한 값을 제공하는 경우가 많다. 따라서 저자들은 RGB 이미지를 기반으로 적응형 깊이 정규화를 위한 gradient-aware depth loss를 제안하였다.
\[\begin{equation} \mathcal{L}_{\hat{D}} = g_\textrm{rgb} \frac{1}{\vert \hat{D} \vert} \sum \log (1 + \| \hat{D} - D \|_1) \\ \textrm{where} \quad g_\textrm{rgb} = \exp (- \nabla I) \end{equation}\]물체의 가장자리와 같이 이미지 gradient가 큰 영역에서는 depth loss가 낮아지며, 매끄러운 영역에서 정규화가 더 강화된다. 또한 실험 결과 로그 페널티가 선형 또는 2차 페널티에 비해 더 부드러운 재구성을 가져온다고 한다.
렌더링된 깊이를 부드럽게 만들기 위해 total variation (TV) loss를 페널티로 사용한다.
\[\begin{equation} \mathcal{L}_{\hat{D}, \textrm{smooth}} = \frac{1}{\vert \hat{D} \vert} \sum_{i, j} (\vert \hat{D}_{i,j} - \hat{D}_{i+1, j} \vert + \vert \hat{D}_{i,j} - \hat{D}_{i, j+1} \vert) \end{equation}\]Monocular depth
깊이 데이터가 포함되지 않은 데이터셋의 경우 monocular depth estimation 네트워크가 추정한 깊이 $D_\textrm{mono}$를 사용한다. ZoeDepth나 DepthAnything을 사용하고 이전 연구와 유사하게 sparse한 SfM 포인트와 비교하여 추정된 깊이와 장면 사이의 스케일 모호성을 해결한다. $D_\textrm{mono}$에 대해 SfM 포인트를 카메라 뷰에 투영하고 아래와 같은 식에서 이미지별 scale 파라미터 $a$와 shift 파라미터 $b$를 구하여 sparse depth map $D_\textrm{sparse}$의 스케일과 일치하도록 스케일을 정렬한다.
\[\begin{equation} \hat{a}, \hat{b} = \underset{a, b}{\arg \min} \sum_{i, j} \| (a D_{\textrm{sparse}, ij} + b) - D_{\textrm{mono}, ij} \|_2^2 \end{equation}\]그런 다음 sensor depth를 사용하는 경우와 동일하게 \(\mathcal{L}_{\hat{D}}\)를 사용한다.
2. Leveraging Normal Cues
최적화하는 동안 Gaussian은 하나의 scaling 축이 다른 두 축보다 훨씬 작은 평평한 디스크 모양이 될 것으로 예상된다. 이 scaling 축은 normal 방향의 근사치 역할을 한다. 구체적으로, quaternion $q$로부터 얻은 rotation matrix $\textbf{R} \in SO(3)$과 scaling factor $s \in \mathbb{R}^3$을 사용하여 각 Gaussian에 대한 normal을 정의한다.
\[\begin{equation} \hat{n}_i = \mathbf{R} \cdot \textrm{OneHot} (\arg \min (s_1, s_2, s_3)) \end{equation}\]여기서 $\textrm{OneHot}(\cdot) \in \mathbb{R}^3$은 scaling이 최소인 곳을 제외하고 모든 곳이 0인 단위 벡터를 반환한다. 올바른 방향을 보장하기 위해 현재 카메라 뷰 방향과 Gaussian normal 사이의 내적이 음수인 경우 normal의 방향을 추가로 뒤집는다. Normal은 카메라 공간으로 변환되고 알파 블렌딩되어 픽셀당 normal 추정치를 제공한다.
\[\begin{equation} \hat{N} = \sum_{i \in \mathcal{N}} \hat{n}_i \alpha_i \prod_{j=1}^{i-1} (1 - \alpha_j) \end{equation}\]Monocular normals

Relightable 3D Gaussian에서는 렌더링된 깊이의 gradient를 구해 ground-truth normal map으로 사용하였다. 하지만, depth map에 잡음이 있으므로 이 방법은 아티팩트를 만든다. 이 방법 대신 Omnidata에서 얻은 더 부드러운 normal map $N$을 사용한다.
추가로 렌더링된 normal map을 부드럽게 만들기 위해 total variation (TV) loss를 페널티로 사용한다.
\[\begin{equation} \mathcal{L}_{\hat{N}, \textrm{smooth}} = \frac{1}{\vert \hat{N} \vert} \sum_{i, j} (\vert \hat{N}_{i,j} - \hat{N}_{i+1, j} \vert + \vert \hat{N}_{i,j} - \hat{N}_{i, j+1} \vert) \end{equation}\]초기 SfM 포인트 클라우드에서 normal 방향을 추정하여 quaternion $q$를 정렬하고, scaling 축 중 하나를 나머지 축보다 작게 초기화한다. 이 초기화는 수렴 속도를 높이는 데 도움이 된다.
3. Optimization
최종 loss는 다음과 같다.
\[\begin{equation} \mathcal{L} = \mathcal{L}_\textrm{rgb} + \lambda_\textrm{depth} (\mathcal{L}_{\hat{D}} + \lambda_\textrm{smooth} \mathcal{L}_{\hat{D}, \textrm{smooth}}) + \lambda_\textrm{normal} (\mathcal{L}_{\hat{N}} + \mathcal{L}_{\hat{N}, \textrm{smooth}}) \end{equation}\]\(\mathcal{L}_\textrm{rgb}\)는 3DGS에서 사용하는 photometric loss이고, 각 가중치는 $\lambda_\textrm{depth} = 0.2$, $\lambda_\textrm{smooth} = 0.5$, $\lambda_\textrm{normal} = 0.1$이다.
4. Meshing
최적화 후 Poisson reconstruction을 적용하여 메쉬를 추출한다. 깊이 정규화의 맥락에서 이미 Gaussian의 위치가 장면 표면을 따라 잘 분산되고 정렬되도록 강제했기 때문에 학습 뷰에서 렌더링된 depth map과 normal map을 직접 back-projection하여 메쉬를 만들기 위한 포인트들을 선택한다.
Experiments
- 데이터셋: MuSHRoom, ScanNet++, Replica, Tanks & Temples
- 구현 디테일
- iteration: 30,000
- Poisson reconstruction 시 200만 개의 점들을 추출하고 depth level 9를 사용
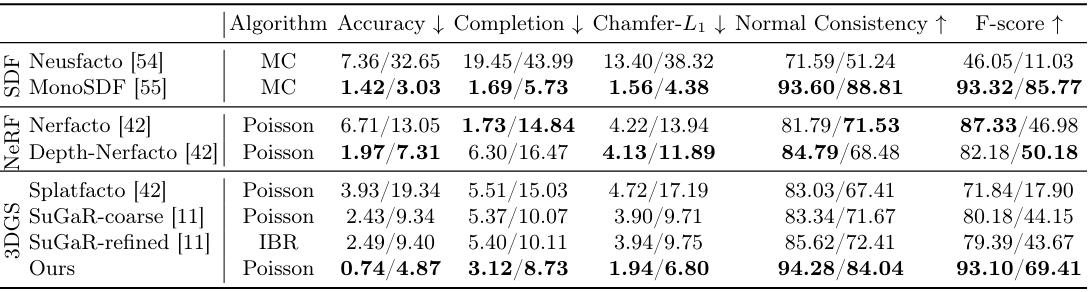
1. Mesh Evaluation
다음은 Replica와 ScanNet++ 데이터셋에서 메쉬 재구성 결과를 비교한 표이다.
다음은 MuSHRoom 데이터셋에서 메쉬 재구성 결과를 비교한 표이다.

다음은 ScanNet++ 데이터셋에서 메쉬 재구성 결과를 비교한 것이다.

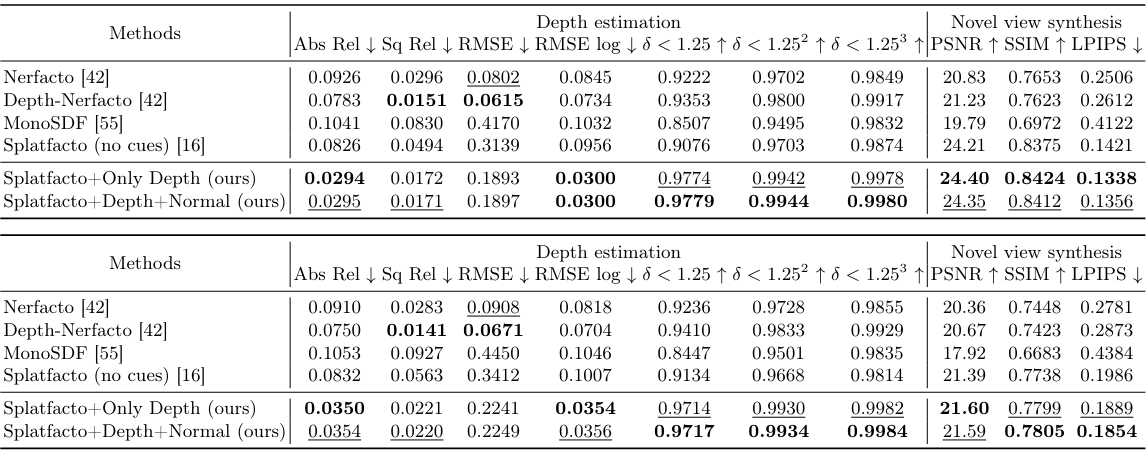
2. Depth Estimation and Novel View Synthesis
다음은 다른 방법들과 렌더링된 깊이 및 RGB 이미지를 비교한 것이다. (MuSHRoom)

다음은 MuSHRoom 데이터셋에서 깊이 추정 및 렌더링 품질을 비교한 표이다. 위는 학습 시퀀스의 매 10 프레임을 test split으로 구성한 것이고 아래는 학습 시퀀스와 겹치지 않는 카메라 궤적에서 test split을 구성한 것이다.
다음은 ScanNet++ 데이터셋에서 깊이 추정 및 렌더링 품질을 비교한 표이다.

3. Ablation Studies
다음은 depth loss에 대한 ablation 결과이다. (ScanNet++)
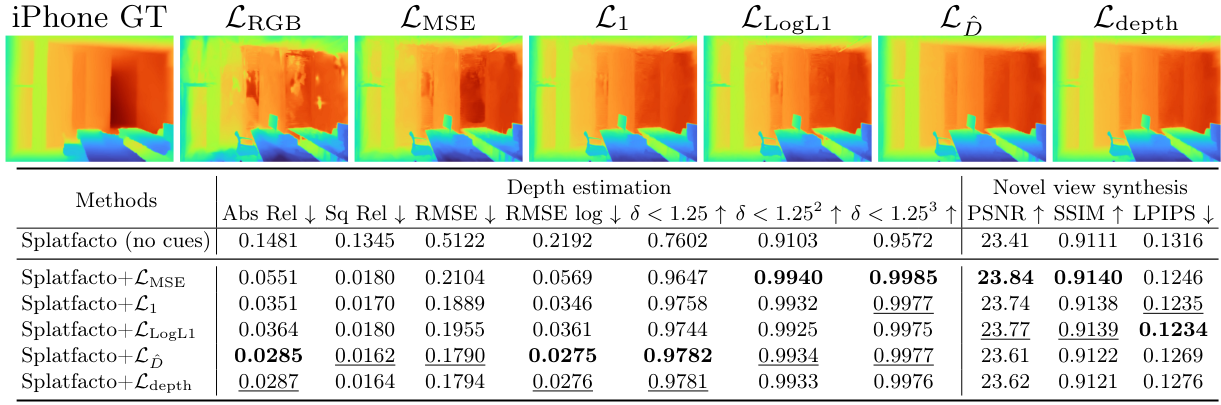
다음은 monocular depth supervision에 대한 ablation 결과이다. (Tanks & Temples - Courtroom)

다음은 메쉬 추출 방법에 대한 ablation 결과이다. Density 0.1~0.5는 SuGaR의 방법을 사용한 것이다. (Replica)

다음은 normal supervision 전략에 대한 ablation 결과이다. (Replica)