[논문리뷰] One-step Diffusion with Distribution Matching Distillation (DMD)
CVPR 2024. [Paper] [Page]
Tianwei Yin, Michaël Gharbi, Richard Zhang, Eli Shechtman, Fredo Durand, William T. Freeman, Taesung Park
MIT | Adobe Research
30 Nov 2023

Introduction
Diffusion model은 안정적인 학습을 통해 전례 없는 수준의 현실감과 다양성을 달성하여 이미지 생성에 혁명을 일으켰다. 그러나 GAN이나 VAE와 달리 샘플링은 점진적인 denoising을 통해 Gaussian noise 샘플을 복잡한 이미지로 변환하는 느리고 반복적인 프로세스이다. 이를 위해서는 일반적으로 수십에서 수백 번의 비용이 많이 드는 신경망 평가가 필요하므로 생성 파이프라인을 사용할 때 상호 작용이 제한된다.
샘플링 속도를 높이기 위해 이전 방법들은 원래의 multi-step diffusion 샘플링에서 발견된 noise-to-image 매핑을 single-pass student model로 증류(distill)하였다. 그러나 이러한 고차원적이고 복잡한 매핑을 피팅하는 것은 까다로운 task이다. 문제는 student model의 한 번의 loss 계산을 실현하기 위해 전체 denoising 궤적을 실행하는 데 드는 비용이 많이 든다는 것이다. 최근 방법은 전체 denoising 시퀀스를 실행하지 않고 student model의 샘플링 거리를 점진적으로 늘려 이를 완화하였다. 그러나 student model의 성능은 원래의 multi-step diffusion model에 비해 여전히 뒤떨어져 있다.
반면 본 논문은 noise와 생성된 이미지 사이의 correspondence를 강화하기보다는 단순히 student가 생성한 이미지가 원래 diffusion model과 구별할 수 없게 보이도록 강제한다. 구체적으로, 사전 학습된 diffusion model을 fine-tuning하여 데이터 분포뿐만 아니라 증류된 generator에 의해 생성되는 가짜 분포도 학습한다. Diffusion model은 score function을 근사화하는 것으로 알려져 있으므로 denoise된 diffusion 출력을 이미지를 “더 사실적”으로 만들기 위한 기울기 방향으로 해석하거나, diffusion model이 가짜 이미지에 대해 학습된 경우 “더 가짜”로 해석할 수 있다. Generator의 기울기 업데이트 규칙은 두 가지의 차이로 합성되어 합성 이미지를 더 높은 현실성과 낮은 fakeness를 향해 나아간다.
또한, 저자들은 적당한 수의 multi-step diffusion 샘플링 결과를 미리 계산하고 one-step 생성과 관련하여 단순 regression loss를 적용하는 것이 분포 매칭 loss가 있는 경우 효과적인 정규화 역할을 한다는 것을 발견했다. 본 논문의 방법은 diffusion model을 사용하여 실제 분포와 가짜 분포를 모델링하고 multi-step diffusion 출력과 매칭하는 단순 regression loss를 사용하여 충실도가 높은 one-step 생성 모델을 학습시킬 수 있음을 보여준다.
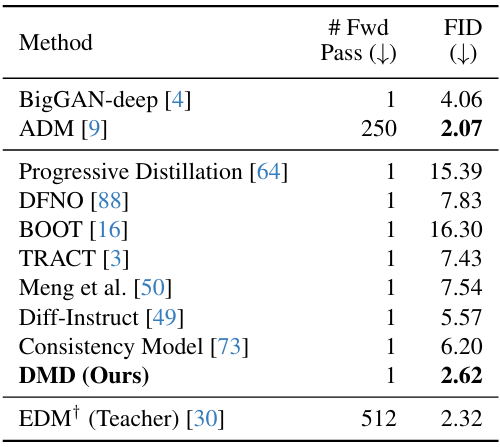
모든 벤치마크에서 본 논문의 one-step generator는 Progressive Distillation, Rectified Flow, Consistency Model과 같은 few-step diffusion 방법보다 훨씬 뛰어난 성능을 발휘한다. 특히 ImageNet에서 DMD는 Consistency Model에 비해 2.4배 향상된 FID 2.62에 도달하였다. Stable Diffusion과 동일한 denoiser 아키텍처를 사용하는 DMD는 MS-COCO 2014-30k에서 11.49의 경쟁력 있는 FID를 달성하였다. DMD에 의해 생성된 이미지는 비용이 많이 드는 Stable Diffusion 모델에 의해 생성된 이미지의 품질과 매우 유사하며, 높은 이미지 충실도를 유지하면서 신경망 평가 횟수를 100배 감소시켰다. 이러한 효율성 덕분에 DMD는 FP16 inference를 활용할 때 1초에 512$\times$512 이미지 20개를 생성할 수 있어 대화형 애플리케이션에 대한 광범위한 가능성을 열어주었다.
Distribution Matching Distillation
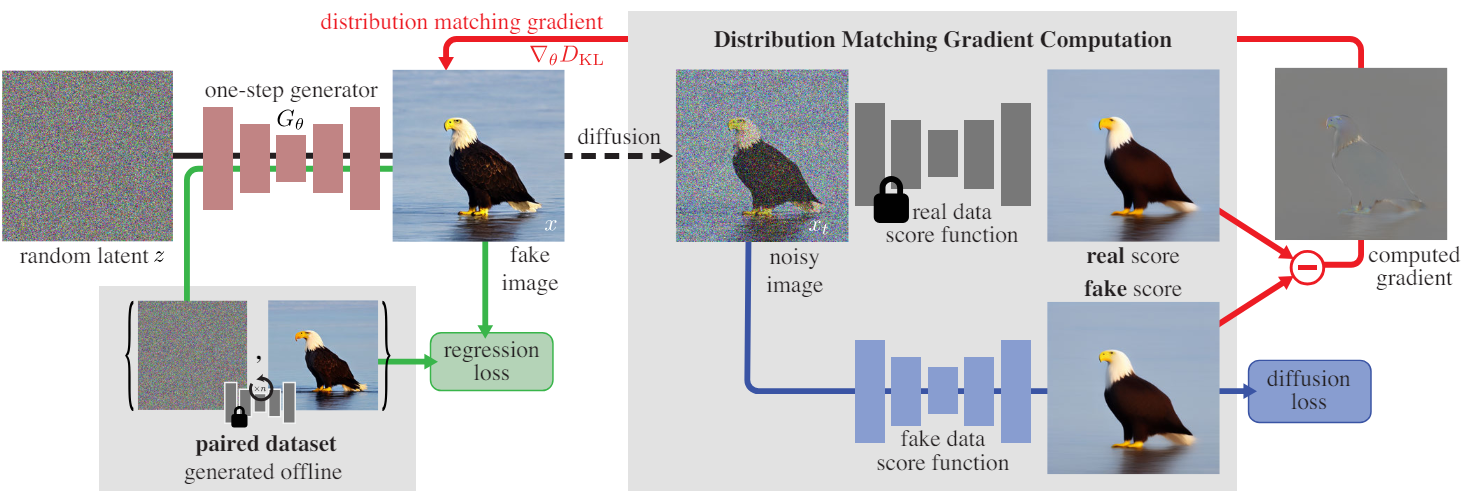
본 논문의 목표는 사전 학습된 diffusion denoiser인 base model $\mu_\textrm{base}$를 비용이 많이 드는 반복적인 샘플링 없이 고품질 이미지를 생성하는 빠른 one-step 이미지 generator $G_\theta$로 증류(distill)하는 것이다. 동일한 분포에서 표본을 생성하기를 바라지만 반드시 정확한 매핑을 재현하려고 하는 것은 아니다.
GAN과 유사하게 학습 분포의 실제 이미지가 아닌 증류된 모델의 출력을 가짜(fake)라 한다. 두 가지 loss의 합을 최소화하여 빠른 generator를 학습시킨다.
- 기울기 업데이트를 두 score function의 차이로 표현할 수 있는 분포 매칭 목적 함수
- Generator가 base model 출력의 대규모 구조와 일치하도록 유도하는 regression loss
저자들은 두 개의 diffusion denoiser를 사용하여 다양한 크기의 Gaussian noise로 교란된 실제 분포와 가짜 분포의 score function을 각각 모델링했다. 또한 classifier-free guidance을 사용하여 학습 프로세스를 조정한다.
1. Pretrained base model and One-step generator
Distillation에서는 사전 학습된 diffusion model $\mu_\textrm{base}$가 제공된다고 가정한다. Diffusion model은 실제 데이터 분포 $x_0 \sim p_\textrm{real}$의 샘플에 noise를 점진적으로 추가하여 이를 $T$ timestep에 걸쳐 white noise $x_T \sim \mathcal{N}(0, \mathbf{I})$로 바꾸는 diffusion process를 역전시키도록 학습된다 ($T = 1000$). 모델은 noise 샘플 $x_T$에서 시작하여 timestep \(t ∈ \{0, 1, \ldots, T − 1\}\)을 조건으로 $x_t$의 noise를 반복적으로 제거하여 타겟 데이터 분포의 샘플을 생성한다. Diffusion model은 사실적인 이미지를 생성하기 위해 일반적으로 수십에서 수백 개의 step이 필요하다.
One-step generator. One-step generator $G_\theta$는 기본 diffusion denoiser의 아키텍처를 가지지만 시간 컨디셔닝은 없다. 학습 전에 base model $G_\theta (z) = \mu_\textrm{base}(z, T−1)$로 파라미터 $\theta$를 초기화한다.
2. Distribution Matching Loss
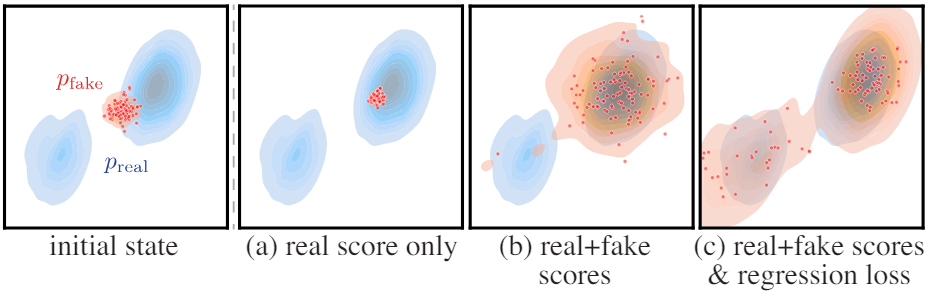
이상적으로는 빠른 generator가 실제 이미지와 구별할 수 없는 샘플을 생성하기를 원한다. ProlificDreamer에서 영감을 받아 실제 이미지 분포 $p_\textrm{real}$과 가짜 이미지 분포 $p_\textrm{fake}$ 사이의 KL divergence 차이를 최소화한다.
이 loss를 추정하기 위해 확률 밀도를 계산하는 것은 일반적으로 다루기 어렵지만 gradient descent로 generator를 학습시키려면 $\theta$에 대한 기울기만 필요하다.
근사 score를 이용한 기울기 업데이트. Generator 파라미터에 대한 위 식의 기울기를 취하면 다음과 같다.
\[\begin{equation} \nabla_\theta D_{KL} = \mathbb{E}_{z \sim \mathcal{N}(0, \textbf{I}), x = G_\theta (z)} [- (s_\textrm{real} (x) - s_\textrm{fake} (x)) \nabla_\theta G_\theta (z)] \end{equation}\]여기서 \(s_\textrm{real} (x)\)과 \(s_\textrm{fake} (x)\)는 각각 실제 분포와 가짜 분포의 score이다. \(s_\textrm{real}\)은 $x$를 \(p_\textrm{real}\)의 모드로 이동시키고 \(−s_\textrm{fake}\)는 두 모드를 분리시킨다. 이 기울기를 계산하는 것은 두 가지 이유로 여전히 어렵다.
- 확률이 낮은 샘플에 대해 score가 발산한다. 특히 가짜 샘플의 경우 $p_\textrm{real}$이 소멸한다.
- Diffusion model은 diffuse된 분포의 score만 제공한다.
본 논문의 전략은 한 쌍의 denoiser를 사용하여 diffusion 후의 실제 분포와 가짜 분포의 score를 모델링하는 것이다. 이 score들을 각각 \(s_\textrm{real} (x_t, t)\)와 \(s_\textrm{fake} (x_t, t)\)로 정의한다. 샘플 $x_t \sim q(x_t \vert x)$는 timestep $t$에서 generator 출력 $x = G_\theta (z)$에 noise를 추가하여 얻는다.
\[\begin{equation} q_t (x_t \vert x) \sim \mathcal{N} (\alpha_t x; \sigma_t^2 I) \end{equation}\]여기서 $\alpha_t$와 $\sigma_t$는 noise schedule에서 나온 것이다.
실제 score. 실제 분포는 base model의 학습 이미지들에 따라 고정되어 있으므로 사전 학습된 \(\mu_\textrm{base}(x, t)\)의 고정 복사본을 사용하여 score를 모델링한다. 주어진 diffusion model에 대한 score는 다음과 같다.
\[\begin{equation} s_\textrm{real} (x_t, t) = - \frac{x_t - \alpha_t \mu_\textrm{base} (x_t, t)}{\sigma_t^2} \end{equation}\]동적으로 학습된 가짜 score. 실제 score와 동일한 방식으로 가짜 score를 도출한다.
\[\begin{equation} s_\textrm{fake} (x_t, t) = - \frac{x_t - \alpha_t \mu_\textrm{fake}^\phi (x_t, t)}{\sigma_t^2} \end{equation}\]그러나 생성된 샘플의 분포가 학습 전반에 걸쳐 변경됨에 따라 가짜 diffusion model \(\mu_\textrm{fake}^\phi\)를 동적으로 조정하여 이러한 변경 사항을 추적한다. 사전 학습된 \(\mu_\textrm{base}\)로 \(\mu_\textrm{fake}^\phi\)를 초기화하고 denoising 목적 함수를 최소화하여 학습 중에 파라미터를 업데이트한다.
\[\begin{equation} \mathcal{L}_\textrm{denoise}^\phi = \| \mu_\textrm{fake}^\phi (x_t, t) - x_0 \|_2^2 \end{equation}\]여기서 \(\mathcal{L}_\textrm{denoise}^\phi\)는 base model 학습 중에 사용된 것과 동일한 가중치 전략을 사용하여 timestep $t$에 따라 가중치가 부여된다.
분포 매칭 기울기 업데이트. 최종 근사 분포 매칭 기울기는 다음과 같다.
\[\begin{aligned} \nabla_\theta D_{KL} &\simeq \mathbb{E}_{z, t, x, x_t} \bigg[ w_t (s_\textrm{fake} (x_t, t) - s_\textrm{real} (x_t, t)) \frac{\partial x_t}{\partial \theta} \bigg] \\ &= \mathbb{E}_{z, t, x, x_t} \bigg[ w_t (s_\textrm{fake} (x_t, t) - s_\textrm{real} (x_t, t)) \frac{\partial x_t}{\partial G_\theta (z)} \frac{\partial G_\theta (z)}{\partial \theta} \bigg] \\ &= \mathbb{E}_{z, t, x, x_t} [ w_t (s_\textrm{fake} (x_t, t) - s_\textrm{real} (x_t, t)) \frac{\partial x_t}{\partial x} \nabla_\theta G_\theta (z) ] \\ &= \mathbb{E}_{z, t, x, x_t} [w_t \alpha_t (s_\textrm{fake} (x_t, t) - s_\textrm{real} (x_t, t)) \nabla_\theta G_\theta (z)] \end{aligned}\]여기서 $z \sim \mathcal{N} (0, \textbf{I})$, $x = G_\theta (z)$, $t \sim \mathcal{U} (T_\textrm{min}, T_\textrm{max})$, $x_t \sim q(x_t \vert x)$이다. DreamFusion을 따라 $T_\textrm{min} = 0.02T$, $T_\textrm{max} = 0.98T$로 설정한다.
$w_t$는 학습 역학을 개선하기 위해 추가하는 시간에 따른 스칼라 가중치이며, 다양한 noise level에 걸쳐 기울기의 크기를 정규화하도록 설계된다. 구체적으로, noise가 제거된 이미지와 입력 사이의 공간 및 채널 차원에 걸쳐 평균 절대 오차를 계산하여 $w_t$를 설정한다.
\[\begin{equation} w_t = \frac{\sigma_t^2}{\alpha_t} \frac{CS}{\| \mu_\textrm{base} (x_t, t) - x \|_1} \end{equation}\]여기서 $S$는 공간적 위치의 수이고 $C$는 채널의 수이다.
3. Regression loss and final objective
분포 매칭 목적 함수는 $t \gg 0$, 즉 생성된 샘플이 많은 양의 noise로 인해 손상된 경우에 대해 잘 정의되어 있다. 그러나 적은 양의 noise의 경우 \(p_\textrm{real} (x_t, t)\)가 0이 되므로 \(s_\textrm{real}(x_t, t)\)는 종종 신뢰할 수 없게 된다. 또한 score $\nabla_x \log(p)$는 확률 밀도 함수 $p$의 scaling에 불변하므로 최적화는 mode collapse/dropping에 취약하다. 여기서 가짜 분포는 모드의 일부분에 더 높은 전체 밀도를 할당한다. 이를 방지하기 위해 추가 regression loss를 사용하여 모든 모드가 보존되도록 한다.
이 loss는 동일한 입력 noise가 주어졌을 때 generator와 base model 출력 사이의 pointwise 거리를 측정한다. 구체적으로, deterministic ODE solver를 사용하여 \(\mu_\textrm{base}\)를 샘플링하여 랜덤 Gaussian noise 이미지 $z$와 해당 출력 $y$의 쌍을 얻고 데이터셋 \(\mathcal{D} = \{z, y\}\)를 구축한다. CIFAR-10의 경우 18 step, ImageNet의 경우 256 step으로 EDM의 Heun solver를 활용했다. LAION의 경우 50개의 샘플링 step을 갖춘 PNDM solver를 사용했다. Regression loss는 다음과 같이 계산된다.
\[\begin{equation} \mathcal{L}_\textrm{reg} = \mathbb{E}_{(z, y) \sim \mathcal{D}} \; \ell (G_\theta (z), y) \end{equation}\]InstaFlow와 Consistency Model를 따라 LPIPS를 거리 함수 $\ell$로 사용한다.
최종 목적 함수 네트워크 \(\mu_\textrm{fake}^\phi\)는 \(\nabla_\theta D_{KL}\)을 계산하는 데 사용되는 \(\mathcal{L}_\textrm{denoise}^\phi\)로 학습된다. $G_\theta$의 경우 최종 목적 함수는 \(\lambda_\textrm{reg} = 0.25\)를 사용하는 \(D_{KL} + \lambda_\textrm{reg} \mathcal{L}_\textrm{reg}\)이다. 두 가지 loss를 서로 다른 데이터 스트림에 적용한다. 분포 매칭 기울기는 쌍이 없는 가짜 샘플을 사용하고 regression loss는 쌍을 이루는 데이터셋을 사용한다.
4. Distillation with classifier-free guidance
Classifier-Free Guidance는 text-to-image diffusion model의 이미지 품질을 향상시키는 데 널리 사용된다. 본 논문의 접근 방식은 classifier-free guidance를 사용하는 diffusion model에도 적용된다. 먼저 \(\mathcal{L}_\textrm{reg}\)에 필요한 쌍을 이루는 데이터셋을 구성하기 위해 가이드된 모델에서 샘플링하여 noise-출력 쌍을 생성한다. 분포 매칭 기울기를 계산할 때 실제 score를 가이드된 모델의 평균 예측에서 파생된 score로 대체한다. 가짜 score에 대한 식은 수정하지 않는다. InstaFlow와 LCM-LoRA를 따라 고정된 guidance scale로 one-step generator를 학습시킨다.
Experiments
1. Class-conditional Image Generation
다음은 ImageNet-64$\times$64에서 샘플 품질을 비교한 표이다.
2. Ablation Studies
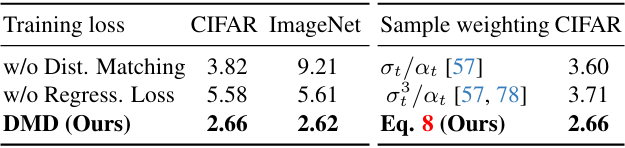
다음은 학습 loss에 대한 ablation study 결과이다.

다음은 학습 loss와 샘플링 가중치에 대한 ablation study 결과이다.
3. Text-to-Image Generation
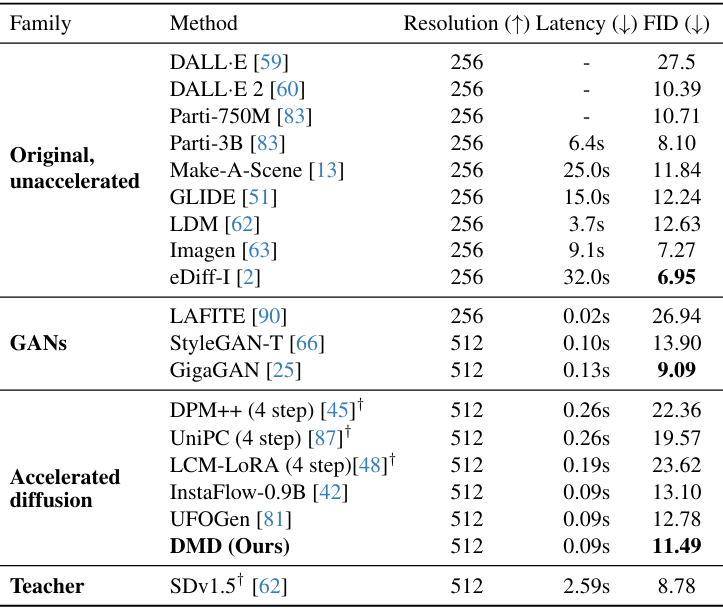
다음은 MS COCO-30k에서 zero-shot text-to-image 생성에 대한 샘플 품질을 비교한 표이다.
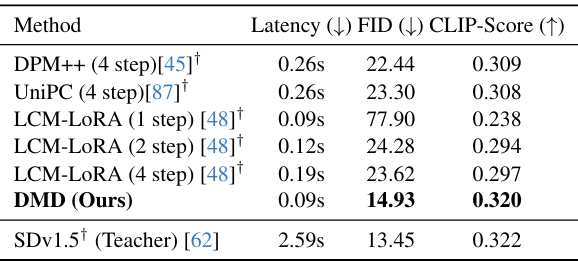
다음은 MS COCO-30K에서 FID와 CLIP-Score를 비교한 표이다.
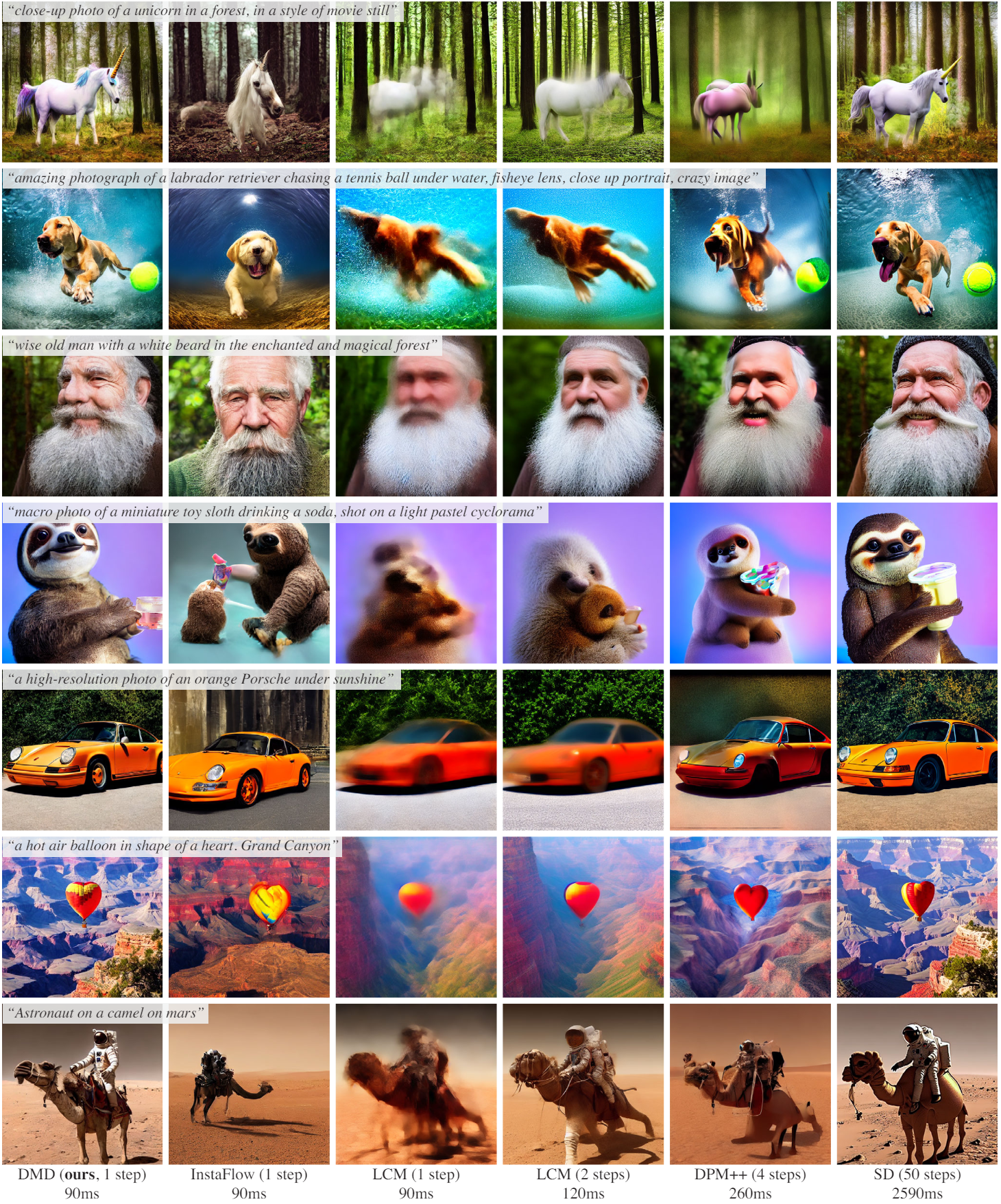
다음은 다른 모델들과 결과를 비교한 것이다.
Limitations
- One-step 모델과 100~1000개의 신경망 평가를 사용하는 샘플링 경로 사이에는 약간의 품질 불일치가 지속된다.
- 모델의 성능은 본질적으로 teacher model의 능력에 제한된다. Stable Diffusion v1.5과 마찬가지로 읽기 쉬운 텍스트나 작은 얼굴 및 사람의 상세한 묘사를 렌더링하는 데 어려움을 겪는다.
- 학습 중에 고정된 guidance scale을 사용한다.