[논문리뷰] Scalable Diffusion Models with Transformers (DiT)
ICCV 2023 (Oral). [Paper] [Page] [Github]
William Peebles, Saining Xie
UC Berkeley | New York University
19 Dec 2022

Introduction
Transformer는 autoregressive model에서 널리 사용되는 반면 다른 생성 모델링 프레임워크에서는 채택률이 낮다. Diffusion model은 이미지 생성 모델의 최근 발전을 주도했지만, 사실상의 backbone으로 convolution U-Net 아키텍처를 채택한다.
DDPM은 diffusion model을 위해 U-Net backbone을 처음 도입했다. 초기에 픽셀 레벨의 autoregressive model과 조건부 GAN에서 성공을 본 U-Net은 몇 가지 변경 사항을 적용하여 PixelCNN++에서 상속되었다. DDPM은 주로 ResNet block으로 구성된 convolution model이다. 표준 U-Net과 달리 Transformer의 필수 구성 요소인 spatial self-attention block이 저해상도에 포함되어 있다. ADM 논문은 adaptive normalization layer와 같은 UNet에 대한 몇 가지 아키텍처 선택을 제거했다. 그러나 DDPM의 UNet에 대한 높은 레벨의 디자인은 대체로 그대로 유지되었다.
저자들은 본 논문을 통해 diffusion model에서 아키텍처 선택의 중요성을 밝히고 미래 생성 모델링 연구를 위한 경험적 기준을 제공하는 것을 목표로 했다. 본 논문은 U-Net inductive bias가 diffusion model의 성능에 중요하지 않으며 Transformer와 같은 표준 디자인으로 쉽게 대체될 수 있음을 보여준다. 결과적으로 diffusion model은 확장성, 견고성, 효율성과 같은 유리한 속성을 유지하는 것뿐만 아니라 다른 도메인의 학습 레시피를 상속함으로써 아키텍처 통합의 최근 추세로부터 이점을 얻을 수 있는 충분한 준비가 되어 있다.
본 논문에서는 Transformer를 기반으로 하는 새로운 종류의 diffusion model에 중점을 둔다. 이것을 Diffusion Transformer 또는 줄여서 DiT라고 부른다. DiT는 기존 convolution 네트워크(ex. ResNet)보다 시각적 인식을 위해 더 효과적으로 확장되는 것으로 나타난 ViT(Vision Transformer)의 모범 사례를 준수한다.
Diffusion Transformers
1. Preliminaries
Diffusion formulation
Diffusion model은 실제 데이터 $x_0$에 점진적으로 noise를 적용하는 forward process를 가정한다.
\[\begin{equation} q(x_t \vert x_0) = \mathcal{N} (x_t; \sqrt{\vphantom{1} \bar{\alpha}_t} x_0, (1 - \bar{\alpha}_t) I) \end{equation}\]Reparameterization trick을 적용하면 다음과 같이 샘플링할 수 있다.
\[\begin{equation} x_t = \sqrt{\vphantom{1} \bar{\alpha}_t} x_0 + \sqrt{1 - \bar{\alpha}_t} \epsilon_t, \quad \epsilon_t \sim \mathcal{N}(0, I) \end{equation}\]Diffusion model은 forward process를 반전시키는 reverse process를 학습한다.
\[\begin{equation} p_\theta (x_{t-1} \vert x_t) = \mathcal{N} (\mu_\theta (x_t), \Sigma_\theta (x_t)) \end{equation}\]여기서 신경망은 $p_\theta$의 통계를 예측하는 데 사용된다. Reverse process 모델은 $x_0$의 log-likelihood의 변동 하한(VLB)으로 학습되며, 이는 다음과 같이 줄일 수 있다.
\[\begin{equation} \mathcal{L} (\theta) = - p(x_0 \vert x_1) + \sum_t \mathcal{D}_\textrm{KL} (q^\ast (x_{t-1} \vert x_t, x_0) \;\|\; p_\theta (x_{t-1} \vert x_t)) \end{equation}\]$q^\ast$와 $p_\theta$는 모두 가우시안이기 때문에 \(\mathcal{D}_\textrm{KL}\)은 두 분포의 평균과 공분산으로 평가할 수 있다. $\mu_\theta$를 noise 예측 네트워크 $\epsilon_\theta$로 다시 parameterize하면 예측된 noise $\epsilon_\theta (x_t)$와 샘플링된 ground-truth Gaussian noise $\epsilon_t$ 사이의 단순한 평균 제곱 오차를 사용하여 모델을 학습할 수 있다.
\[\begin{equation} \mathcal{L}_\textrm{simple} (\theta) = \| \epsilon_\theta (x_t) - \epsilon_t \|_2^2 \end{equation}\]그러나 학습된 reverse process 공분산 $\Sigma_\theta$로 diffusion model을 학습하려면 전체 \(\mathcal{D}_\textrm{KL}\) 항을 최적화해야 한다. 저자들은 ADM의 접근 방식을 따른다. \(\mathcal{L}_\textrm{simple}\)로 $\epsilon_\theta$를 학습하고 전체 $\mathcal{L}$로 $\Sigma_\theta$를 학습한다. $p_\theta$가 학습되면 \(x_{t_\textrm{max}} \sim \mathcal{N} (0, I)\)을 초기화하고 $x_{t−1} \sim p_\theta (x_{t-1} \vert x_t)$를 샘플링하여 새 이미지를 샘플링할 수 있다.
Classifier-free guidance
Conditional diffusion model은 클래스 레이블 $c$와 같은 추가 정보를 입력으로 사용한다. 이 경우 reverse process는 $p_\theta (x_{t-1} \vert x_t, c)$가 되며, 여기서 $\epsilon_\theta$와 $\Sigma_\theta$는 $c$로 컨디셔닝된다. 이 설정에서 classifier-free guidance를 사용하여 샘플링 절차가 $\log p(c \vert x)$가 높은 $x$를 찾도록 장려할 수 있다. 베이즈 정리에 따라
\[\begin{equation} \log p(c \vert x) \propto \log p(x \vert c) − \log p(x) \end{equation}\]이고, 따라서
\[\begin{equation} \nabla_x \log p (c \vert x) \propto \nabla_x \log p(x \vert c) - \nabla_x \log p(x) \end{equation}\]이다. Diffusion model의 출력을 score function으로 해석하면 DDPM 샘플링 절차는 다음과 같이 $p(x \vert c)$가 높은 샘플 $x$로 유도할 수 있다.
\[\begin{aligned} \hat{\epsilon}_\theta (x_t, c) &= \epsilon_\theta (x_t, \emptyset) + s \cdot \nabla_x \log p(x \vert c) \\ &\propto \epsilon_\theta (x_t, \emptyset) + s \cdot ( \epsilon_\theta (x_t, c) − \epsilon_\theta (x_t, \emptyset)) \end{aligned}\]여기서 $s > 1$은 guidance의 척도를 나타낸다. $c = \emptyset$으로 diffusion model을 평가하는 것은 학습 중에 $c$를 임의로 삭제하고 학습된 “null” 임베딩 $\emptyset$으로 대체하여 수행된다. Classifier-free guidance는 일반 샘플링 기술에 비해 상당히 개선된 샘플을 생성하는 것으로 널리 알려져 있으며 이러한 추세는 DiT 모델에도 적용된다.
Latent diffusion models
고해상도 픽셀 space에서 직접 diffusion model을 학습하는 것은 계산적으로 불가능 할 수 있다. Latent diffusion model (LDM)은 2단계 접근 방식으로 이 문제를 해결한다.
- 학습된 인코더 $E$를 사용하여 이미지를 더 작은 space의 표현으로 압축하는 오토인코더를 학습한다.
- 이미지 $x$의 diffusion model 대신 표현 $z = E(x)$의 diffusion model을 학습한다 ($E$는 고정).
그런 다음 diffusion model에서 표현 $z$를 샘플링하고 학습된 디코더 $x = D(z)$를 사용하여 이미지로 디코딩하여 새 이미지를 생성할 수 있다.
LDM은 ADM과 같은 픽셀 space diffusion model의 Gflops의 일부를 사용하면서 우수한 성능을 달성한다. 본 논문은 컴퓨팅 효율성에 관심이 있기 때문에 아키텍처 탐색을 위한 매력적인 출발점이 된다. 본 논문에서는 DiT를 수정하지 않고 픽셀 space에도 적용할 수 있지만 latent space에 DiT를 적용한다. 이는 이미지 생성 파이프라인을 하이브리드 기반 접근 방식, 즉 기존 convolution VAE와 Transformer 기반 DDPM을 사용하여 만든다.
2. Diffusion Transformer Design Space
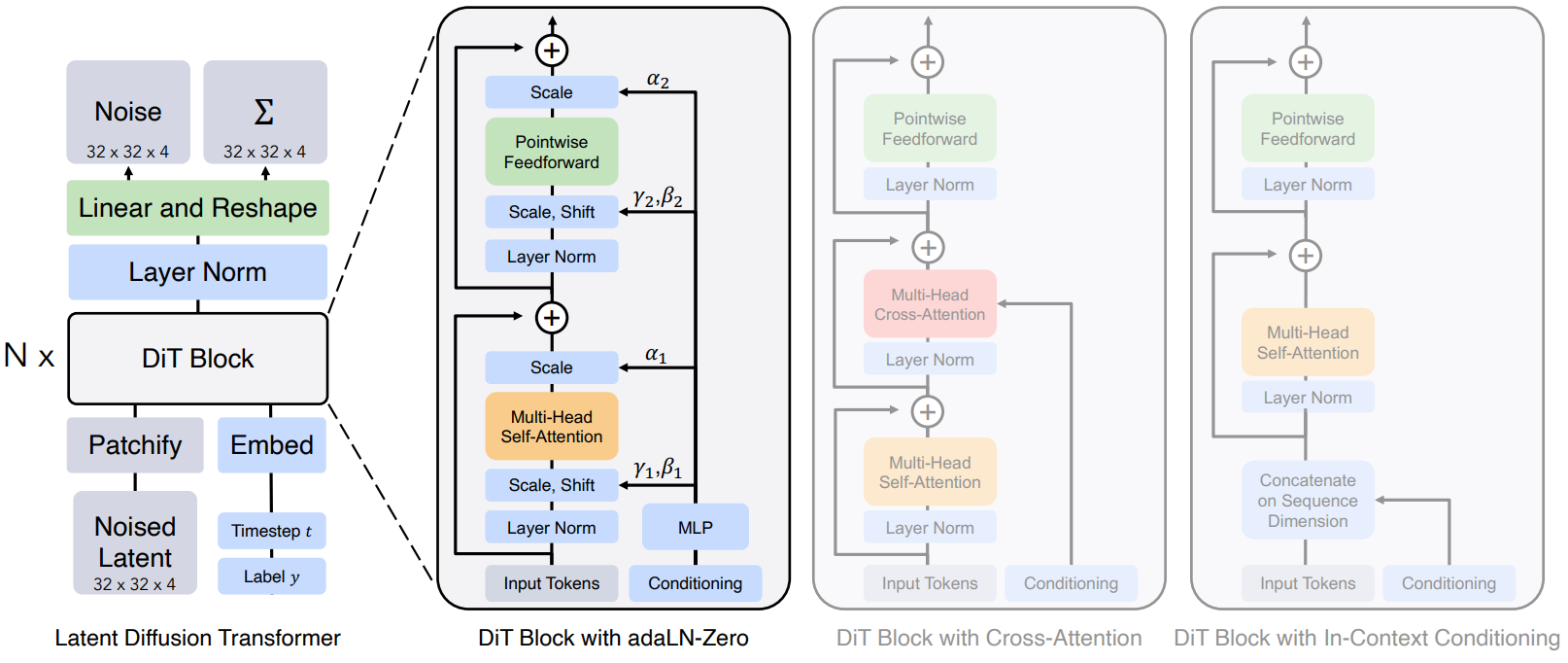
본 논문은 diffusion model을 위한 새로운 아키텍처인 DiT를 소개한다. 스케일링 속성을 유지하기 위해 가능한 한 표준 Transformer 아키텍처에 충실하는 것을 목표로 한다. 본 논문의 초점은 이미지의 DDPM을 학습하는 것이므로 DiT는 일련의 패치에서 작동하는 ViT 아키텍처를 기반으로 한다. DiT는 ViT의 많은 좋은 속성을 유지한다. 아래 그림은 전체 DiT 아키텍처의 개요를 보여준다.
Patchify
DiT에 대한 입력은 공간적 표현 $z$이다 (256$\times$256$\times$3 이미지의 경우 $z$는 32$\times$32$\times$4 모양). DiT의 첫 번째 계층은 “patchify”로, 입력에 각 패치를 선형으로 삽입하여 입력을 차원 $d$의 $T$개의 토큰 시퀀스로 변환한다. 그 이후 표준 ViT의 주파수 기반 위치 임베딩(사인-코사인 버전)을 모든 입력 토큰에 적용한다. Patchify에 의해 생성된 토큰 $T$의 수는 패치 크기 hyperparameter $p$에 의해 결정된다.
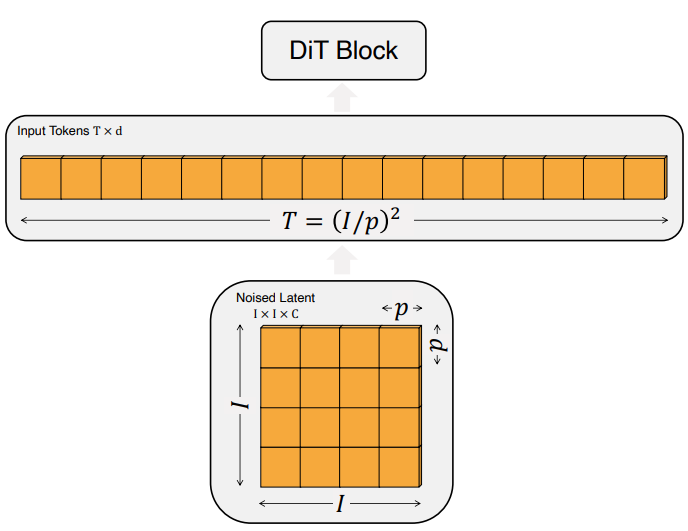
위 그림에서 볼 수 있듯이 $p$를 절반으로 줄이면 $T$가 4배가 되고 따라서 전체 Transformer의 Gflops는 적어도 4배가 된다. Gflops에 상당한 영향을 미치기는 하지만 $p$를 변경해도 다운스트림 파라미터 수에는 의미 있는 영향이 없다.
DiT block design
Patchify 후 입력 토큰은 일련의 Transformer block에 의해 처리된다. Noise가 있는 이미지 입력 외에도 diffusion model은 때때로 timestep $t$, 클래스 레이블 $c$, 자연어 등과 같은 추가 조건부 정보를 처리한다. 저자들은 조건부 입력을 다르게 처리하는 다음과 같은 Transformer block의 4가지 변형을 살펴본다. 이 디자인들은 표준 ViT 블록 디자인에 작지만 중요한 수정 사항을 도입하였다.
- In-context conditioning: 단순히 $t$와 $c$의 벡터 임베딩을 입력 시퀀스에 두 개의 추가 토큰으로 추가하여 이미지 토큰과 다르지 않게 취급한다. 이는 ViT의 cls 토큰과 유사하며 수정 없이 표준 ViT 블록을 사용할 수 있다. 마지막 블록 이후 시퀀스에서 컨디셔닝 토큰을 제거한다. 이 접근 방식은 무시할 수 있는 새로운 Gflops를 모델에 도입한다.
- Cross-attention block: $t$와 $c$의 임베딩을 이미지 토큰 시퀀스와 별도로 길이가 2인 시퀀스로 concat한다. Transformer block은 multi-head self-attention block 다음에 추가 multi-head cross-attention layer를 포함하도록 수정되었다. 또한 LDM에서 클래스 레이블로 컨디셔닝하는 데 사용하는 것과 유사하다. Cross-attention은 대략 15%의 오버헤드로 모델에 가장 많은 Gflops를 추가한다.
- Adaptive layer norm (adaLN) block: GAN의 adaptive normalization layer와 UNet backbone이 있는 diffusion model의 광범위한 사용에 따라 Transformer block의 표준 레이어를 adaptive layer norm (adaLN)으로 대체하는 방법을 모색한다. 차원별 scaling 및 shift 파라미터 $\gamma$와 $\beta$를 직접 학습하는 대신 $t$와 $c$의 임베딩 벡터 합계에서 회귀한다. 세 가지 블록 디자인 중에서 adaLN은 최소한의 Gflops를 추가하므로 가장 컴퓨팅 효율적이다. 또한 모든 토큰에 동일한 feature를 적용하도록 제한되는 유일한 컨디셔닝 메커니즘이다.
- adaLN-Zero block: ResNet에 대한 이전 연구들에서는 각 residual block을 항등 함수로 초기화하는 것이 유익하다는 것을 발견했다. Diffusion U-Net 모델은 유사한 초기화 전략을 사용하여 residual 연결 전에 각 블록의 최종 convolution layer를 0으로 초기화한다. $\gamma$와 $\beta$를 회귀하는 것 외에도 DiT 블록 내의 residual 연결 직전에 적용되는 차원별 scaling 파라미터 $\alpha$도 회귀한다. 모든 $\alpha$에 대해 영벡터를 출력하도록 MLP를 초기화한다. 이는 전체 DiT 블록을 항등 함수로 초기화한다. adaLN 블록과 마찬가지로 adaLNZero는 무시할 수 있는 Gflops를 모델에 추가한다.
Model size
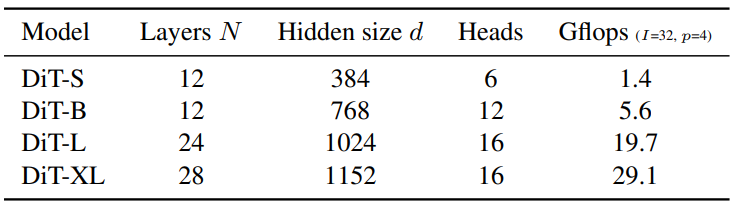
Hidden dimension 크기 $d$에서 각각 작동하는 일련의 $N$개의 DiT 블록을 적용한다. ViT에 이어 $N$, $d$, attention head를 공동으로 확장하는 표준 Transformer 구성을 사용한다. 특히 DiT-S, DiT-B, DiT-L, DiT-XL의 네 가지 구성을 사용한다. 0.3에서 118.6 Gflops까지 다양한 모델 크기와 flops 할당을 다루므로 확장 성능을 측정할 수 있다. 아래 표는 구성에 대한 세부 정보를 제공한다.
Transformer decoder
최종 DiT 블록 후에 이미지 토큰 시퀀스를 출력 noise 예측과 출력 대각 공분산 예측으로 디코딩해야 한다. 이 두 출력은 모두 원래 입력과 모양이 같다. 이를 위해 표준 선형 디코더를 사용한다. 최종 layer norm (adaLN을 사용하는 경우 adaLN)을 적용하고 각 토큰을 $p \times p \times 2C$ 텐서로 선형 디코딩한다. 여기서 $C$는 DiT에 대한 입력의 채널 수이다. 마지막으로 예측된 noise와 공분산을 얻기 위해 디코딩된 토큰을 원래 공간적 레이아웃으로 재정렬한다.
Experiments
- 데이터셋: ImageNet (256$\times$256, 512$\times$512)
- 학습
- Learning rate: $1 \times 10^{-4}$ (warmup은 사용하지 않음)
- Optimizer: AdamW
- weight decay: 사용하지 않음
- batch size: 256
- data augmentation: horizontal flip
- EMA decay: 0.9999
- Diffusion
- VAE: Stable Diffusion의 VAE 사용 (downsample factor 8)
- $t_\textrm{max} = 1000$
- Noise schedule: 선형, $1 \times 10^{-4}$에서 $2 \times 10^{-2}$
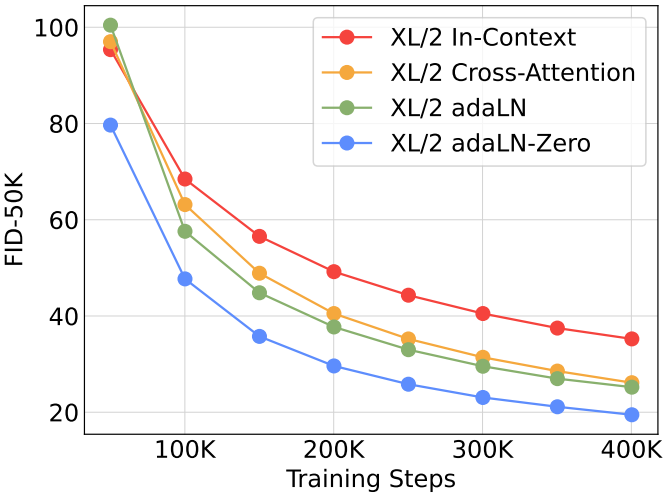
DiT block design
다음은 다양한 컨디셔닝 전략을 비교한 그래프이다.
Scaling model size and patch size
다음은 모델의 크기에 따른 FID를 비교한 그래프이다.
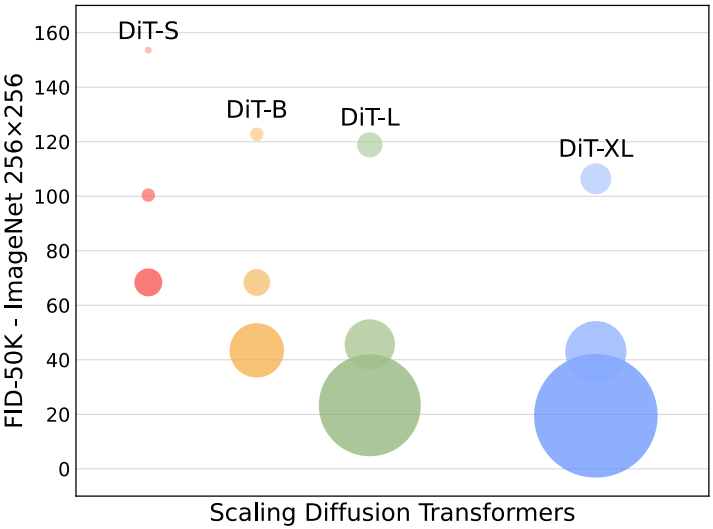
다음은 다양한 DiT 모델의 크기에 따른 FID의 변화를 나타낸 그래프이다.
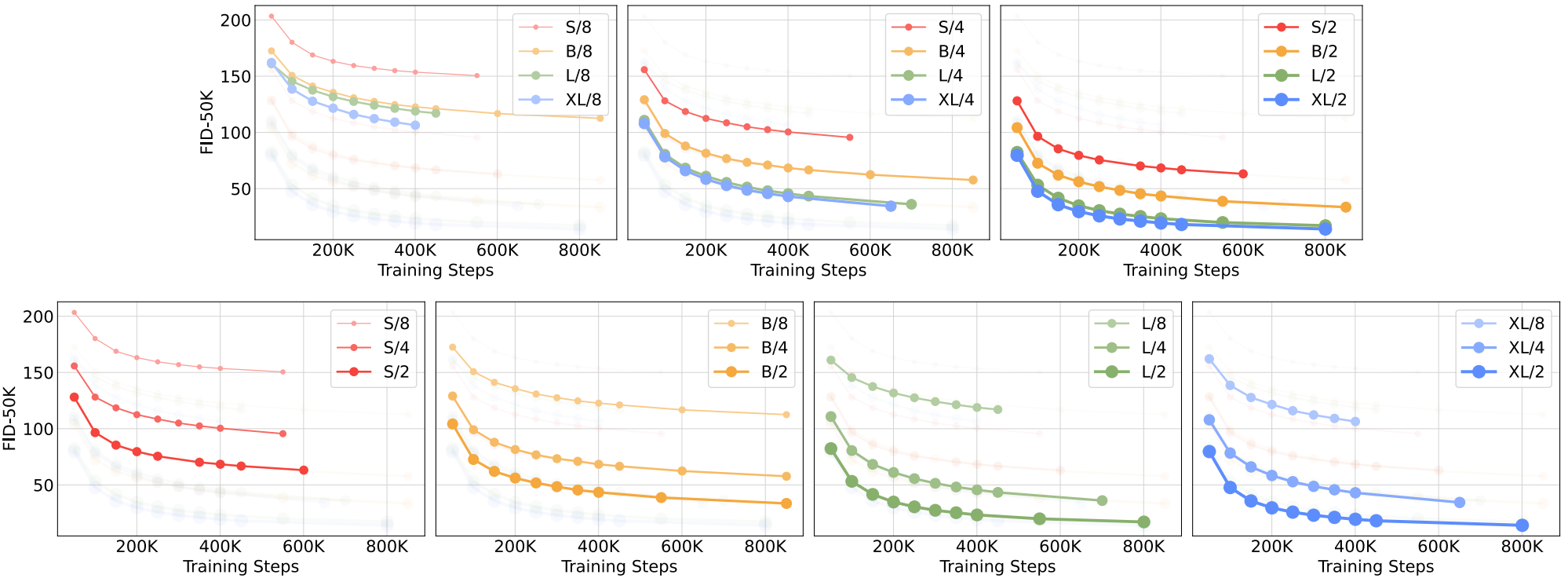
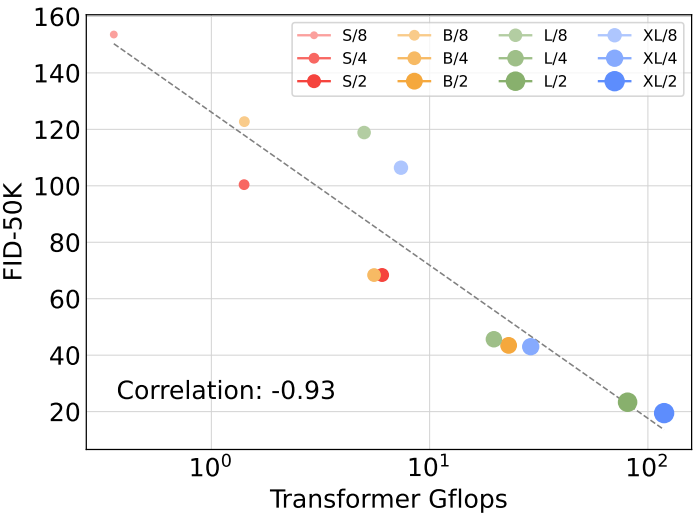
DiT Gflops are critical to improving performance
다음은 Gflops에 따른 FID를 나타낸 그래프이다.
Larger DiT models are more compute-efficient
다음은 학습에 사용된 Gflops에 따른 FID를 나타낸 그래프이다.
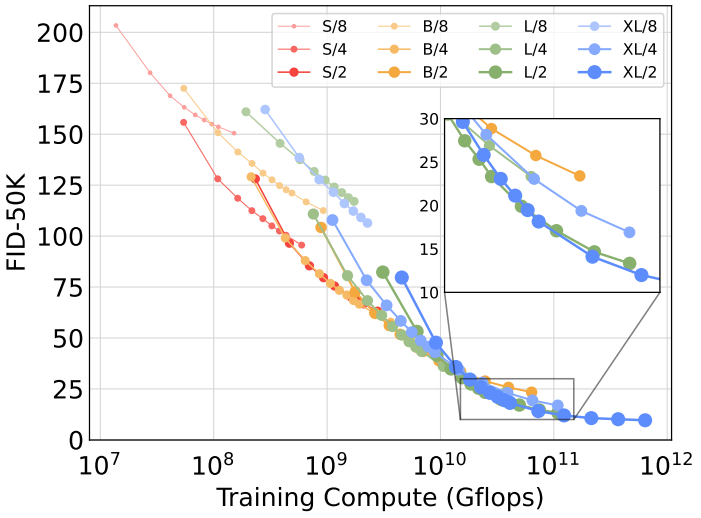
Visualizing scaling
다음은 패치 사이즈와 Transformer 크기에 따른 이미지 품질 변화이다.

1. State-of-the-Art Diffusion Models
256$\times$256 ImageNet
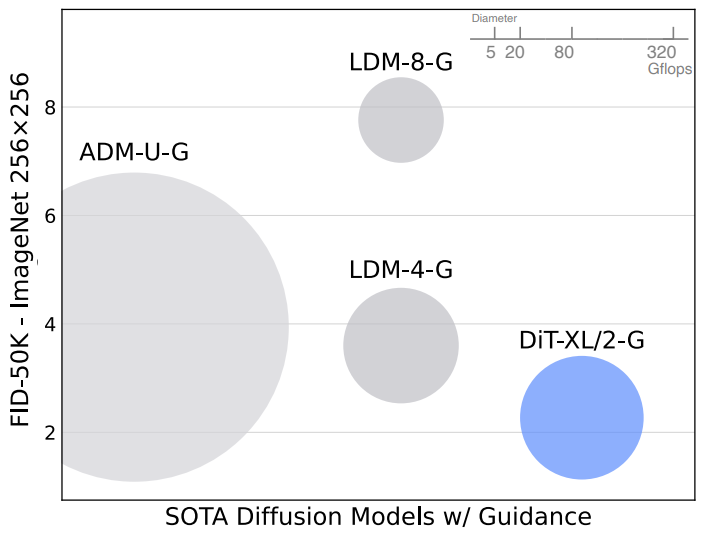
다음은 다양한 SOTA 클래스 조건부 생성 모델들과 모델의 크기 및 FID를 비교한 그래프이다.
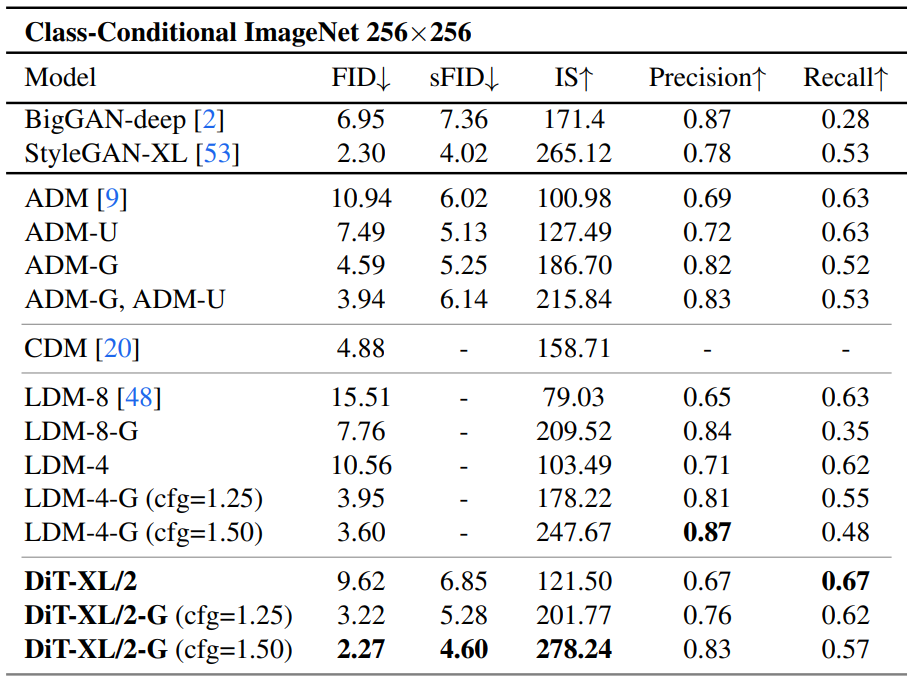
다음은 ImageNet 256$\times$256에서 클래스 조건부 생성 모델들과 성능을 비교한 표이다.
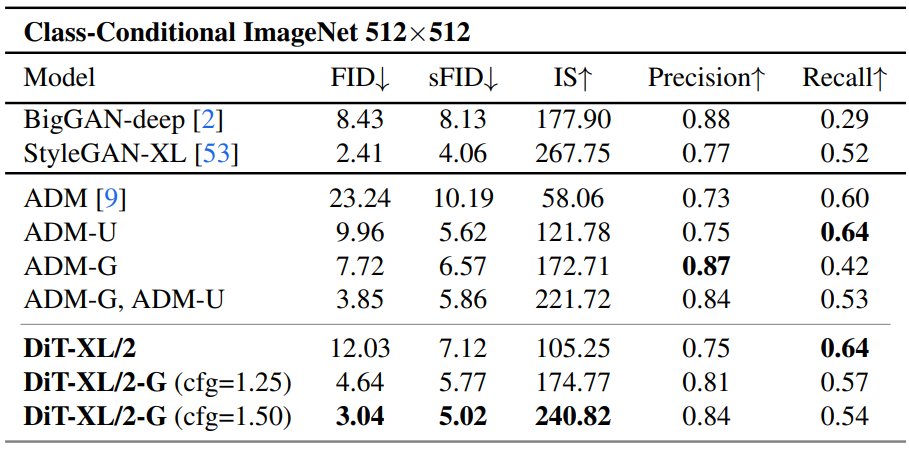
512$\times$512 ImageNet
다음은 ImageNet 512$\times$512에서 클래스 조건부 생성 모델들과 성능을 비교한 표이다.
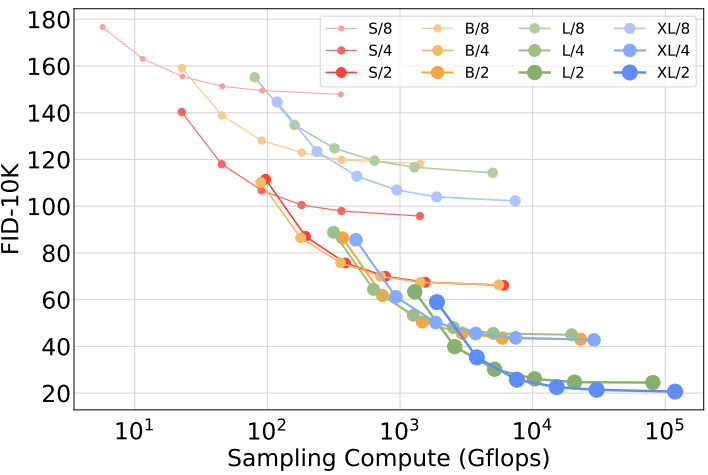
2. Scaling Model vs. Sampling Compute
다음은 샘플링 시 사용되는 Gflops에 따른 FID를 나타낸 그래프이다.