[논문리뷰] Refining Generative Process with Discriminator Guidance in Score-based Diffusion Models
ICML 2023 (Oral). [Paper] [Github]
Dongjun Kim, Yeongmin Kim, Wanmo Kang, Il-Chul Moon
KAIST | NAVER Cloud
28 Nov 2022

Introduction
Diffusion model은 최근 이미지 생성 등의 분야에서 SOTA를 기록하였다. SOTA model이 인간 수준의 생성을 수행하지만 아직 diffusion model에 대한 깊은 이해를 위한 연구가 많이 필요하다.
Diffusion model의 추정 대상이 diffusion model 간에 데이터 score로 고정되어 있고 새 모델을 학습하는 데 계산 비용이 많이 들기 때문에 하위 task에 널리 사용되는 잘 학습된 score model을 공유한다. 그러나 CIFAR-10에 대한 대부분의 이전 연구는 FID가 2.20 근처에서 포화 상태이며, 사전 학습된 score network를 추가로 학습하거나 diffusion 전략을 다양화하거나 다양한 네트워크 구조를 통합해도 크게 개선되지 않는다.
본 논문에서는 주어진 사전 학습된 score network의 샘플 품질을 개선하기 위한 새로운 접근 방식을 소개한다. 사전 학습된 score 추정과 실제 데이터 score 사이의 차이를 직접 정량화하고 보조 discriminator를 통해 이 차이를 추정한다. Discriminator는 diffusion model에 추가적인 자유도를 제공하며, 저자들은 discriminator가 score 학습으로 캡처되지 않은 의미있는 정보를 효과적으로 찾는다는 것을 증명한다. 사전 학습된 score 추정에 대한 추정된 차이를 합산하여 조정된 score를 구성하고 이 조정은 CIFAR-10, CelebA, FFHQ, ImageNet 256x256에서 새로운 SOTA 성능을 달성하였다. Discriminator는 매우 빠르게 포화되므로 (10 Epoch 이내) 저렴한 비용으로 상당한 성능 향상을 달성할 수 있다.
Preliminary
Forward diffusion process는 반복적으로 Gaussian noise를 더해 데이터를 손상시킨다.
\[\begin{equation} x_{t+1} = \sqrt{1 - \beta_t} x_t + \beta_t \epsilon_t, \quad \epsilon_t \sim \mathcal{N}(0,I) \end{equation}\]Diffusion process는 SDE로 일반화할 수 있다.
\[\begin{equation} dx_t = f(x_t, t) dt + g(t) dw_t \end{equation}\]Forward SDE는 유일한 reverse diffusion process
\[\begin{equation} dx_t = [f(x_t, t) - g^2 (t) \nabla \log p_r^t (x_t)] d \bar{t} + g(t) d \bar{w}_t \end{equation}\]를 가진다. $\bar{t}$는 reverse-time이고 $\bar{w}_t$는 reverse-time Brownian motion이다. 시작과 끝의 시간이 같다면 이 reverse SDE의 해는 forward SDE의 해와 일치한다.
Diffusion model은 score network $s_\theta$를 학습시켜 tractable하지 않은 데이터 score $\nabla \log p_r^t (x_t)$를 추정하며, 다음과 같은 목적 함수가 사용된다.
\[\begin{equation} \mathcal{L}_\theta = \frac{1}{2} \int_0^T \xi (t) \mathbb{E} [\| s_\theta (x_t, t) - \nabla \log p_r^t (x_t) \|_2^2 ] dt \end{equation}\]$\xi$는 시간적 가중치이다. 이 목적 함수는 noise 추정
\[\begin{equation} \sum \mathbb{E}[ \|\epsilon_\theta - \epsilon \|_2^2 ] \end{equation}\]이나 데이터 재구성
\[\begin{equation} \sum \mathbb{E} [ \| \hat{x}_\theta (x_t) - x_0 \|_2^2 ] \end{equation}\]으로 동등하게 해석할 수 있다.
Refining Generative Process with Discriminator Guidance
1. Correction of Pre-trained Score Estimation
Score가 학습된 후, reverse-time 생성 프로세스
\[\begin{equation} dx_t = [f(x_t, t) - g^2 (t) s_{\theta_\infty} (x_t, t)] d \bar{t} + g(t) d \hat{w}_t \end{equation}\]로 샘플을 합성할 수 있다. 여기서 $s_{\theta_\infty}$는 수렴한 이후의 score network이다. 만일 $\theta_\infty$가 전역 최적값 $\theta_\ast$을 빗나가면 생성 프로세스는 reverse-time 데이터 프로세스와 다르다. 따라서 score 추정치를 조정하면 생성 프로세스를 reverse-time 데이터 프로세스와 같게 만들 수 있을 것이다. 이 차이를 correction term $c_{\theta_\infty} (x_t, t)$이라 하며 생성 프로세스는 다음과 같이 다시 정의된다.
\[\begin{equation} dx_t = [f(x_t, t) - g^2 (t) (s_{\theta_\infty} + c_{\theta_\infty}) (x_t, t)] d \bar{t} + g(t) d \bar{w}_t \\ c_{\theta_\infty} := \nabla \log \frac{p_r^t (x_t)}{p_{\theta_\infty}^t (x_t)} \end{equation}\]2. Discriminator Guidance
Density-ratio $p_r^t / p_{\theta_\infty}^t$를 알 수 없기 때문에 correction term $c_{\theta_\infty} (x_t, t)$은 일반적으로 tractable하지 않다. 따라서 discriminator를 학습시켜 density-ratio를 추정해야 한다. Discriminator의 학습에는 Binary Cross Entropy (BCE)를 사용한다.
\[\begin{aligned} \mathcal{L}_\phi = & \int \lambda (t) (\mathbb{E}_{p_r^t (x_t)} [-\log d_\phi (x_t, t)] \\ & + \mathbb{E}_{p_{\theta_\infty}^t} [-\log (1 - d_\phi (x_t, t))]) dt \end{aligned}\]$\lambda$는 시간적 가중치이다. Discriminator는 diffuse된 실제 데이터 $x_t \sim p_r^t$를 진짜로, diffuse된 샘플 데이터 $x_t \sim p_{\theta_\infty}^t$를 가짜로 분류한다. 자세한 알고리즘은 Algorithm 1과 같다.

그런 다음 correction term을
로 표현하면, $c_{\theta_\infty}$를 discriminator $d_\phi$를 이용하여 추정할 수 있다.
\[\begin{equation} c_{\theta_\infty} (x_t, t) \approx c_\phi (x_t, t) := \nabla \log \frac{d_\phi (x_t, t)}{1 - d_\phi (x_t, t)} \end{equation}\]위의 tractable한 correction 추정값을 사용하여 Discriminator Guidance (DG)를 다음과 같이 정의할 수 있다.
\[\begin{equation} dx_t = [f(x_t, t) - g^2 (t) (s_{\theta_\infty} + c_\phi) (x_t, t)] d \bar{t} + g(t) d \bar{w}_t \end{equation}\]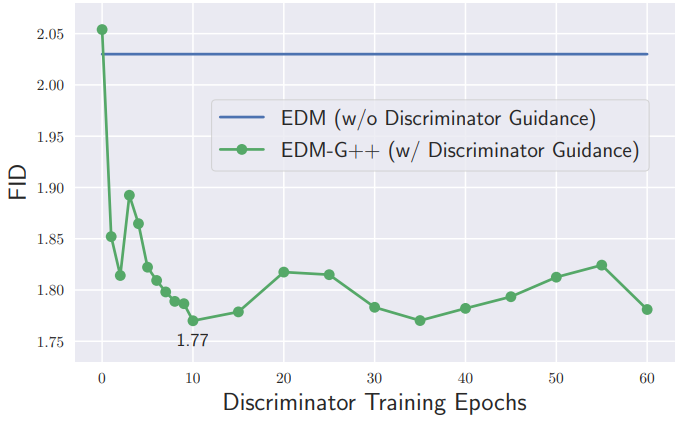
위 그림은 discriminator가 학습됨에 따라 샘플 품질이 개선되며 빠르게 수렴함을 보여준다.
3. Theoretical Analysis
Discriminator Guidance를 미분 방정식 관점에서 설명하는 대신 샘플 분포와 데이터 분포 사이의 분포 불일치로 설명할 수 있다. $p_{\theta_\infty, \phi}$를 discriminator guidance의 샘플 분포라 하자. 그러면 $p_{\theta_\infty, \phi}$가 $p_{\theta_\infty}$보다 데이터 분포 $p_r^t$에 가까운 지 질문할 수 있다. 이 질문에 답하기 위해 다음과 같이 KL-divergence를 정의할 수 있다.
\[\begin{aligned} D_{KL} (p_r \| p_{\theta_\infty}) &= D_{KL} (p_r^T \| \pi) + E_{\theta_\infty} \\ D_{KL} (p_r \| p_{\theta_\infty, \phi}) &\le D_{KL} (p_r^T \| \pi) + E_{\theta_\infty, \phi} \end{aligned}\] \[\begin{aligned} E_{\theta_\infty} &= \frac{1}{2} \int_0^T g^2 (t) \mathbb{E}_{p_r^t} [ \| \nabla \log p_r^t - s_{\theta_\infty} \|_2^2 ] dt \\ E_{\theta_\infty, \phi} &= \frac{1}{2} \int_0^T g^2 (t) \mathbb{E}_{p_r^t} [ \| \nabla \log p_r^t - (s_{\theta_\infty} + c_\phi) \|_2^2 ] dt \\ &= \frac{1}{2} \int_0^T g^2 (t) \mathbb{E}_{p_r^t} [ \| c_{\theta_\infty} - c_\phi \|_2^2 ] dt \end{aligned}\]두 KL-divergence를 빼면 discriminator 학습의 gain을 얻을 수 있다.
\[\begin{equation} D_{KL} (p_r \| p_{\theta_\infty, \phi}) \le D_{KL} (p_r \| p_{\theta_\infty}) - \textrm{Gain} (\theta_\infty, \phi) \\ \textrm{Gain} (\theta_\infty, \phi) = E_{\theta_\infty} - E_{\theta_\infty, \phi} \end{equation}\]만일 discriminator가 전혀 학습되지 않았다면 ($d_{\phi_0} \approx 0.5$) gain은 근사적으로 0이다. 최적의 discriminator는 $E_{\theta_\infty, \phi} = 0$이므로 gain이 최대화된다.
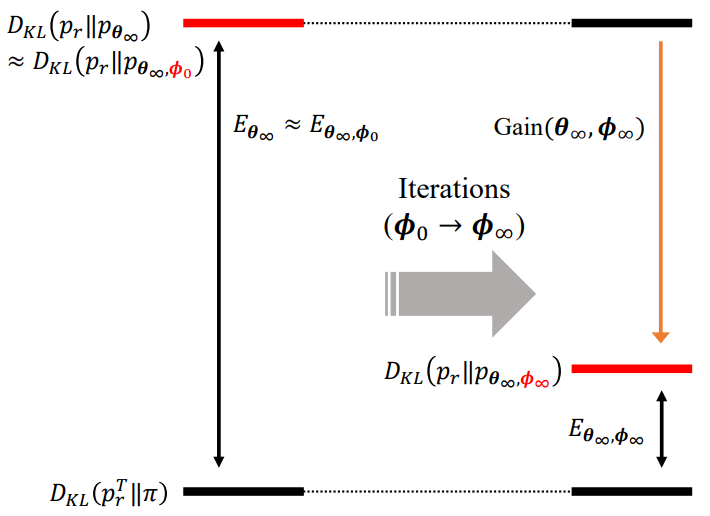
다르게 말하면, discriminator guidance가 추가적인 축 방향 자유도 $\phi$를 두어 score error $E_{\theta_\infty}$를 discriminator error $E_{\theta_\infty, \phi}$로 reparameterize한다고 할 수 있다. $E_{\theta_\infty}$는 더 이상 $L_\theta$로 최적화할 수 없지만 $E_{\theta_\infty, \phi}$는 대체 loss $\mathcal{L}_\phi$로 최적화할 수 있다. (위 그림 참고)
4. Connection with Classifier Guidance
Classifier Guidance (CG)는 샘플을 사전 학습된 classifier $p_{\psi_\infty} (c \vert x_t, t)$로 guide하는 중요한 테크닉이다. Classifier 기반 생성 프로세스는
\[\begin{equation} dx_t = [f(x_t, t) - g^2 (t) (s_{\theta_\infty} (x_t, t) + \nabla \log p_{\psi_\infty} (y \vert x_t, t))] d \bar{t} + g_t d \bar{w}_t \end{equation}\]이다.
\[\begin{aligned} \nabla \log p_r^t(x_t, y) &= \nabla \log p_r^t (x_t) + \nabla \log p(y \vert x_t, t) \\ & \approx s_{\theta_\infty} (x_t, t) + \nabla \log p_{\psi_\infty} (y \vert x_t, t) \end{aligned}\]이기 때문에, $(x_t, y)$의 결합 분포에서 샘플링하는 것과 동등하다. Classifier guidance는 샘플이 클래스 레이블 $y$에 맞게 분류되는지 아닌지를 평가하여 샘플 경로에 보조 정보를 제공한다. 반면, discriminator guidance는 레이블에 구애받지 않으며 샘플 경로가 현실적인지 비현실적인지에 대한 고유한 정보를 제공한다.
$(x_t, y)$의 결합 분포에서 샘플링은 score 추정이 정확한 경우에만 유효하므로 discriminator guidance는 부정확한 score 추정을 조정하여 classifier guidance와 시너지 효과를 낼 수 있다. 저자들은 다음과 같은 guidance의 결합을 제안한다.
\[\begin{aligned} dx_t = & [f(x_t, t) - g^2 (t) ((s_{\theta_\infty} + w_t^\textrm{DG} c_{\phi_\infty}) (x_t, t) \\ & + w_t^{CG} \nabla \log p_{\psi_\infty} (c \vert x_t, t))] d \bar{t} + g(t) d \bar{w}_t \end{aligned}\]$w_t^\textrm{DG}$와 $w_t^\textrm{CG}$는 시간 종속 가중치이다. 두 가지 정보는 보완적인 방식으로 샘플을 classifier와 discriminator의 공통 영역으로 이상적으로 guide할 수 있다.

Algorithm 2는 guidance 테크닉의 샘플링 절차의 전체 디테일을 설명한다. 이 알고리즘은 아래 표의 해당 하이퍼파라미터를 사용하여 DDPM, DDIM, EDM의 sampler를 줄인다. 본 논문의 sampler는 기본 sampler 뒤에 G++를 붙여 표시한다.

Experiments
1. A Toy 2-dimensional Case
다음은 tractable한 2차원 toy case의 실험 결과를 보여준다.
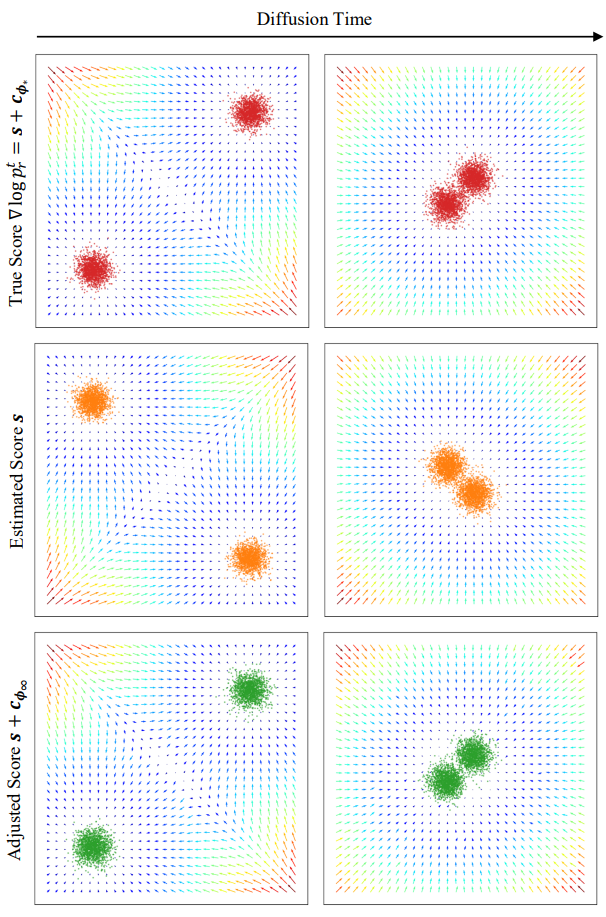
저자들은 256개의 뉴런으로 이루어진 4-layered MLP discriminator를 수렴할 때까지 학습시켰다. 저자들은 데이터 score에 부적합한 잘못된 score function $s := \nabla \log p_g^t$를 가정한다. Guidance가 없는 경우 잘못된 score $s$는 그림의 두번째 행과 같이 잘못된 분포에서 샘플을 생성한다. 반대로 $s + c_{\phi_\infty}$는 $s$를 $\nabla \log p_r^t$로 성공적으로 guide한다.
2. Image Generation
저자들은 CIFAR-10, CelebA/FFHQ 64$\times$64, ImageNet 256$\times$256에서 실험을 진행하였다. CIFAR-10과 FFHQ는 EDM, CelebA는 STDDPM, ImageNet은 ADM을 사전 학습된 모델로 사용하였다.
Discriminator Network
U-Net 구조의 인코더를 discriminator network로 사용하였다. Pixel-diffusion models의 경우 사전 학습된 ADM classifier와 보조 U-Net 인코더를 붙여 사용한다. $(x_t, t)$를 ADM classifier에 입력하여 latent $z_t$를 추출하고 $(z_t, t)$를 보조 U-Net 인코더에 넣어 출력의 진짜/가짜를 예측한다. ADM classifier는 freeze하고 U-Net 인코더만 fine-tuning한다. Latent-diffusion model의 경우 처음부터 U-Net 인코더를 학습시킨다.
Quantitative Analysis
실험 결과, 모든 데이터셋에 대해 새로운 SOTA FID를 달성하였다. 다음은 CIFAR-10에서의 성능을 나타낸 표이다.
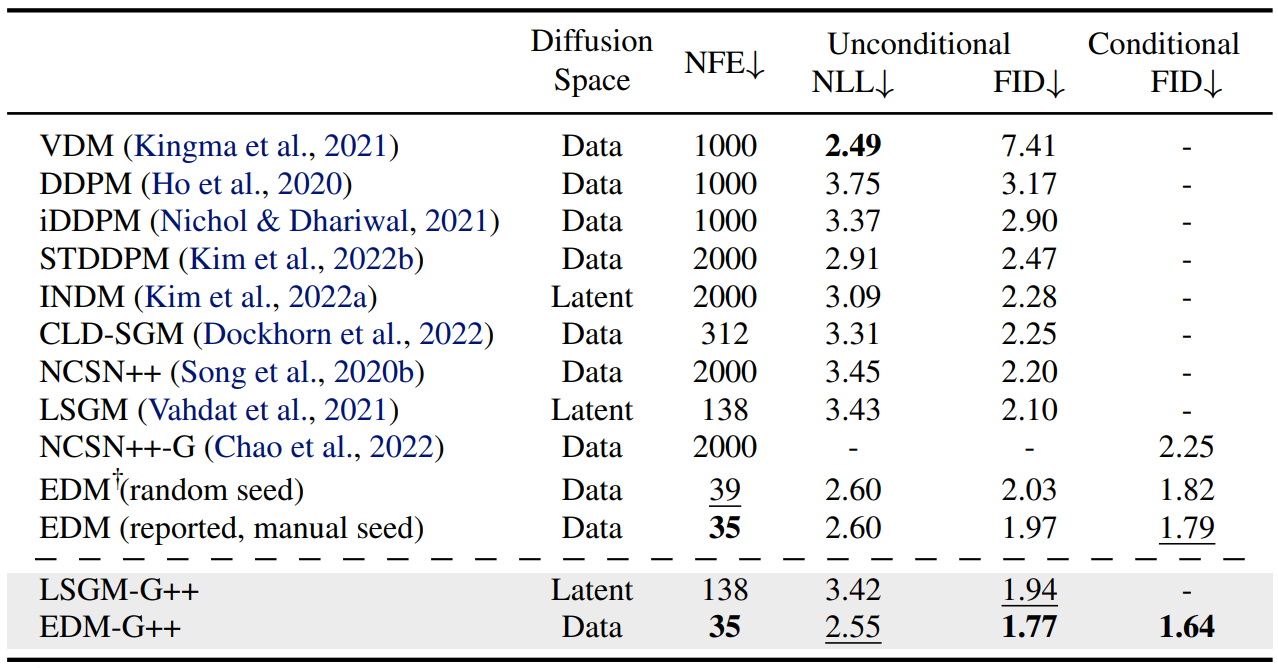
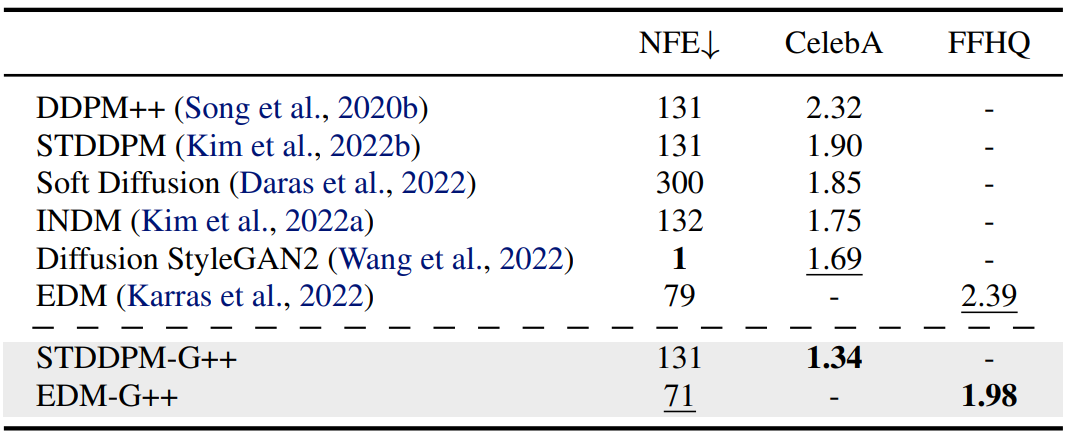
Discriminator Guidance가 pixel-diffusion model (EDM)과 latent-diffusion model (LSGM) 모두에서 효과적임을 보여준다. EDM과 LSGM 모두 hyperparameter를 그대로 사용하였기 때문에 성능 개선은 순수하게 DG에 의한 것이다. 다음은 CelebA와 FFHQ에서의 FID를 비교한 것이다.
다음은 ImageNet 256$\times$256에서의 성능을 나타낸 표이다.
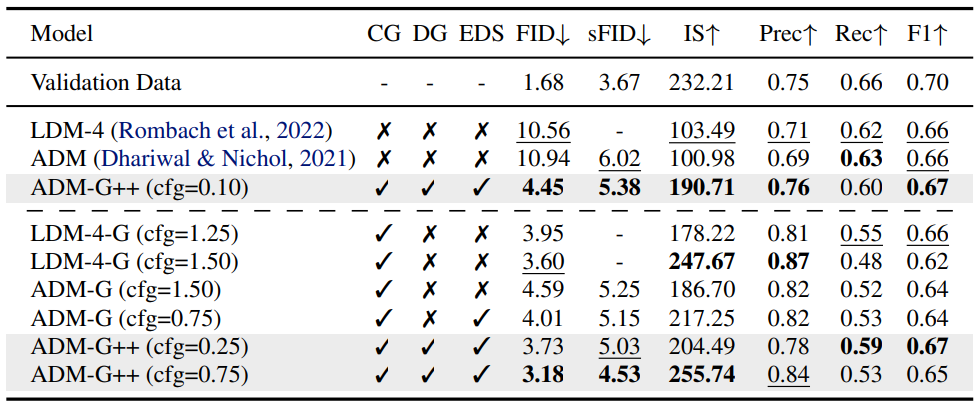
모델의 IS와 precision이 validation dataset 수준에 도달하였으며, FID, sFID, recall과 같은 다른 metric을 최적화하는 것이 더 중요해졌다. 한편, FID와 recall 사이의 trade-off가 존재한다.
Qualitative Analysis
다음은 ImageNet 256$\times$256에서의 샘플을 비교한 것이다. (a)는 ADM, (b)는 classifier guidance를 사용한 ADM, (c)는 classifier guidance와 discriminator guidance를 사용한 ADM의 샘플이다.

다음은 원본 샘플, EDM과 EDM-G++로 재생성한 샘플 100개의 평균을 나타낸 그림이다. 원본 샘플을 표준 가우시안의 random noise로 손상시킨 뒤 probability flow ODE를 풀어 재생성한 것이다.

이상적인 경우 sampler가 deterministic하므로 score 추정이 정확하다면 완벽한 재생성이 가능하다. EDM으로 재생성한 경우 forward SDE와 generative SDE 사이의 불일치가 발생하였지만 EDM-G++는 generative SDE가 수정되어 forward process와 거의 동일해졌다.
다음은 FFHQ에서 density-ratio에 따른 샘플 궤적들을 비교한 그래프이다.
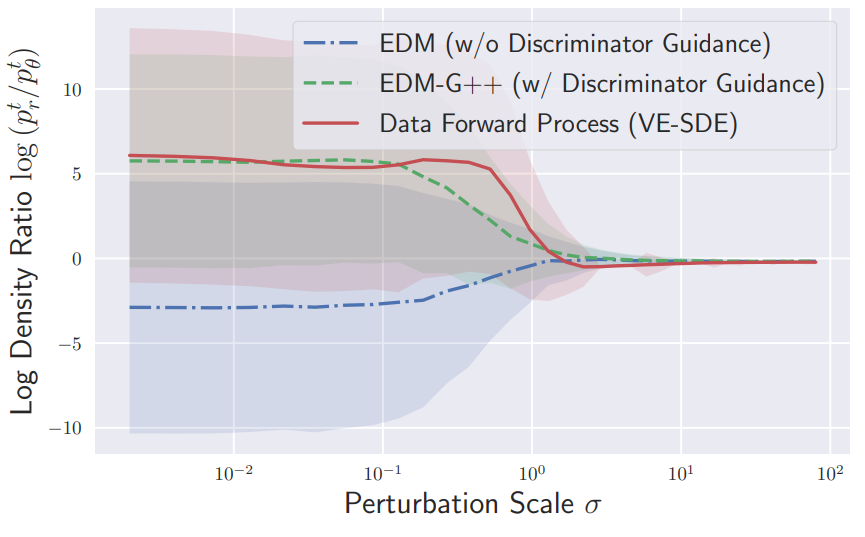
학습된 discriminator가 정확하게 실제 데이터와 샘플 데이터의 diffusion 경로를 구분하는 것을 볼 수 있다. 조정된 score를 활용하여 생성된 샘플 경로는 discriminator를 속이고 조정된 generative SDE의 density-ratio 곡선이 데이터 forward SDE의 곡선에 근접하게 된다.
다음은 CIFAR-10에서 샘플링 시의 함수 평가 횟수 (NFE)에 따른 DG의 효과를 나타낸 그래프이다.
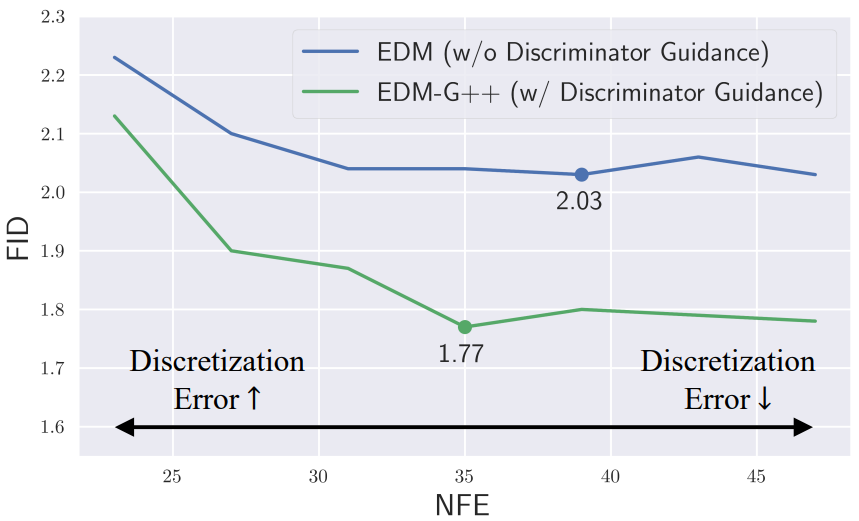
NFE가 감소하면 이산화 오차가 샘플링 오차의 대부분을 차지하며, DG에 의한 gain이 suboptimal해진다.
다음은 ImageNet 256에서 negative log-likelihood \(-\log \mathcal{N}(F(x); \mu_{data}, \Sigma_{data})\)를 나타낸 그래프이다. $F(x)$는 sFID의 feature map으로, 공간적 feature를 캡처하는 데 특화되어 있다.
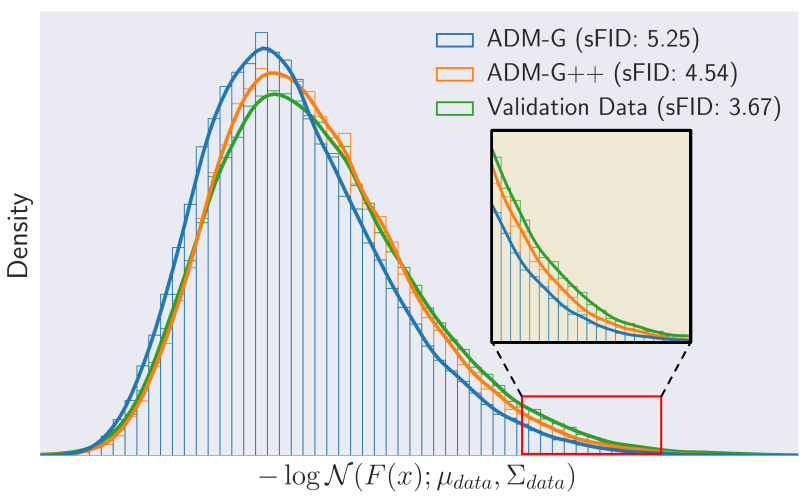
ADM-G++의 feature 분포는 validation data에 가까워지며, ADM-G++는 자주 보이는 데이터뿐만 아니라 학습중에 드물게 관찰되는 데이터도 잘 생성한다.
3. Image-2-Image Translation
다음은 I2I task에 대한 그림이다. (a)는 SDEdit에 DG를 적용하여 translation 품질을 개선한 것이고, (b)는 realism (FID)와 faithfulness (PSNR) 사이의 그래프이다.

(a)를 보면 DG는 source 도메인이나 translated 도메인에 가지 않고 target 도메인으로 연결된다. (b)를 보면 DG가 realism과 faithfulness 사이의 trade-off를 해결한다.