[논문리뷰] Photorealistic Object Insertion with Diffusion-Guided Inverse Rendering

ECCV 2024. [Paper] [Page]
Ruofan Liang, Zan Gojcic, Merlin Nimier-David, David Acuna, Nandita Vijaykumar, Sanja Fidler, Zian Wang
NVIDIA | University of Toronto | Vector Institute
19 Aug 2024

Introduction

가상 물체 삽입은 다양한 응용을 가능하게 한다. 사실적인 삽입을 위해서는 가상 물체와 환경 간의 상호 작용을 충실하게 모델링해야 한다. (ex. specular highlight, 그림자)

표준 가상 물체 삽입 파이프라인은 일반적으로 세 가지 핵심 단계를 포함한다.

1. 입력 이미지에서 조명 추정
2. 3D proxy geometry 생성
3. 렌더링 엔진에서 합성 이미지 렌더링

입력 이미지에서 조명을 추정하는 것은 가장 중요하지만 여전히 미해결 문제이다. 조명 추정은 제한된 입력을 처리할 때 특히 어렵다. 실제로 inverse rendering은 근본적으로 무수히 해가 많은 문제이다.

이전 방법들은 수작업으로 prior를 정의하거나 데이터에서 학습하는 것을 목표로 했다. 그러나 전자는 실제 장면에 적용하면 종종 문제가 생기고 후자는 GT 데이터의 부족으로 어려움을 겪는다. 결과적으로 이러한 알고리즘은 종종 특정 도메인 (ex. 실내 또는 실외 장면)에 크게 맞춤화된다.

이러한 한계를 해결하기 위해, 저자들은 대규모 diffusion model에서 학습한 강력한 이미지 생성 prior를 inverse rendering을 위한 guidance로 재사용할 것을 제안하였다. 종종 특정 도메인에 국한되는 기존 prior와 달리, diffusion model은 방대한 데이터셋에서 학습되고 세상과 기본 물리적 개념에 대한 놀라운 이해를 보여준다. Diffusion model은 여전히 ​​그림자와 반사와 같은 정확한 조명 효과를 생성하지 못하는 경우가 많지만, 물리 기반 렌더러와 결합하고 장면에 맞게 조정하면 귀중한 guidance를 제공할 수 있다.

구체적으로, 저자들은 세 가지 주요 기여를 바탕으로 Diffusion Prior for Inverse Rendering (DiPIR)을 제시하였다.

1. 물리 기반 렌더러를 사용하여 빛과 3D 에셋 간의 상호 작용을 정확하게 시뮬레이션하여 최종 합성 이미지를 생성한다. 또한 카메라 센서를 모방하기 위해 알려지지 않은 톤 매핑 곡선을 고려한다.
2. 입력 이미지와 삽입된 에셋의 유형을 기반으로 사전 학습된 diffusion model의 가벼운 개인화(personalization) 체계를 제안하였다.
3. 이 개인화를 활용하고 학습 안정성을 개선하는 SDS loss의 변형을 설계하였다.

DiPIR에서 diffusion model은 인간 평가자와 비슷하게 행동한다. 편집된 이미지를 입력으로 받고 피드백 신호를 미분 가능한 렌더링을 통해 물리 기반 장면 속성으로 전파하여 end-to-end 최적화를 가능하게 한다. DiPIR은 실내 및 실외 데이터셋에서 물체를 삽입하는 데 있어 기존의 SOTA 조명 추정 방법보다 성능이 우수하다.

Method

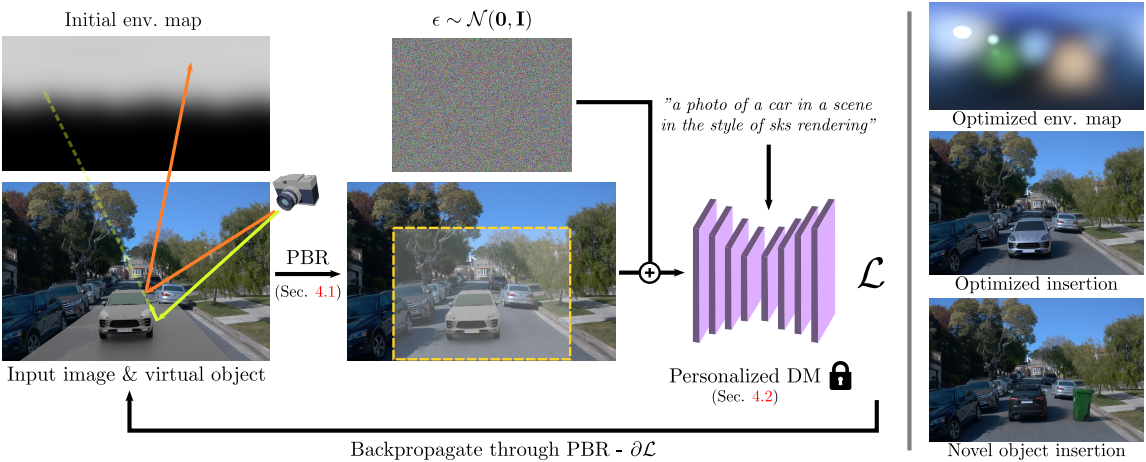
1. Physically-based Virtual Object Insertion

가상 장면

가상 물체 $\mathcal{X}$를 이미지 \(\textbf{I}_\textrm{bg} \in \mathbb{R}^{h \times w \times 3}\)에 삽입하려면 올바른 카메라 포즈에서 본 3D 가상 장면을 만들어야 한다. 여기서는 사용자가 $\mathcal{X}$에 대한 특정 포즈를 제공한다고 가정하지만, 어떤 경우에는 바닥 평면과 장면 크기를 감지하여 적절한 포즈를 자동으로 결정할 수도 있다.

$\mathcal{X}$에 의해 생긴 그림자와 같은 효과를 원래 이미지에 모델링하기 위해 알려진 proxy geometry $\mathcal{P}$도 가정한다. 저자들은 가상 물체 아래에 간단한 평면을 놓는 것이 충분하다는 것을 발견했다. 이 평면은 깊이 데이터나 LiDAR 데이터를 기반으로 수동 또는 자동으로 생성하여 쉽게 배치할 수 있다.

빛 표현

장면의 조명 $\textbf{L}$을 $N$개의 최적화 가능한 Spherical Gaussian (SG) 파라미터 \(\{\textbf{c}_k, \boldsymbol{\mu}_k, \sigma_k\}_{k=1}^N \in \mathbb{R}^{N \times 7}\)의 집합으로 표현한다. 여기서 방향 $\textbf{v} \in \mathbb{R}^3$에서 하나의 SG lobe에 대한 radiance는 다음과 같이 정의된다.

\[\begin{equation} \textbf{G}_k (\textbf{v}; \textbf{c}_k, \boldsymbol{\mu}_k, \sigma_k) = \textbf{c} \exp (- \frac{1 - \textbf{v} \cdot \boldsymbol{\mu}}{\sigma^2}) \end{equation}\]

전체 environment map $\textbf{L} \in \mathbb{R}^{H \times W \times 3}$은 다음과 같이 계산된다.

\[\begin{equation} \textbf{L}_{i,j} = \sum_{k=1}^N \textbf{G}_k (\textbf{v}_{i,j}; \textbf{c}_k, \boldsymbol{\mu}_k, \sigma_k) \end{equation}\]

SG 기반 조명 표현은 우수한 수렴 특성과 단순성을 위해 선택되었지만 많은 대안이 존재하며 본 논문의 방법과 결합될 수 있다.

미분 가능한 렌더링

장면에 가상 물체를 삽입하는 것은 최적화 가능한 environment map과 삽입된 가상 물체의 상호작용과 삽입된 물체가 배경 장면에 미치는 효과를 시뮬레이션하는 것을 포함한다.

전경 이미지. 최적화된 조명 표현 $\textbf{L}$과 가상 물체 $\textbf{X}$ (기하학적 구조 + 재료)가 주어지면 삽입된 물체의 전경 이미지 \(\textbf{I}_\textrm{fg}\)는 표준 path tracing을 사용하여 직접 렌더링할 수 있다.

\[\begin{equation} \textbf{I}_\textrm{fg} = \textrm{PathTrace}(\mathcal{X}, \textbf{L}, D) \end{equation}\]

$D$는 빛 경로에서의 상호작용의 최대 수이다. 제공된 proxy geometry가 정확하거나 재료가 있다고 가정하지 않기 때문에, 예를 들어 매우 반사성이 강한 삽입된 물체로 인해 물체에서 장면으로 반사되는 빛의 효과를 생략한다.

그림자 비율. 배경 이미지 \(\textbf{I}_\textrm{bg}\)가 이미 장면을 충실히 표현하고 있으므로, 삽입된 물체의 외형과 물체가 proxy geometry $\mathcal{P}$에 만든는 그림자를 시뮬레이션하는 데 국한된다.

주변 장면에 대한 물체의 효과를 설명하는 그림자 비율 \(\beta_\textrm{shadow} \in \mathbb{R}^{h \times w \times 3}\)은 삽입된 물체가 있는 경우와 없는 경우에 $\mathcal{P}$가 받은 radiance의 비율로 계산된다. \(\beta_\textrm{shadow}\)의 낮은 값은 강하게 그림자가 진 영역을 나타낸다.

\[\begin{equation} \boldsymbol{\beta}_\textrm{shadow} = \frac{\textrm{PathTrace}(\mathcal{X} \cup \mathcal{P}, \textbf{L}, 1)}{\textrm{PathTrace}(\mathcal{P}, \textbf{L}, 1)} \end{equation}\]

샘플링 효율성을 위해 조명과 BSDF 사이에 Multiple Importance Sampling (MIS)을 사용한다. 최대 경로 길이는 메모리와 계산 비용을 줄이기 위해 1개의 상호작용으로 제한되었다. $\mathcal{P}$와 함께 특정 재료 정보가 제공되지 않는 한, Lambertian BSDF를 사용하는데, 이 경우 albedo은 분자/분모에서 상쇄된다. 실제로, 그림자 비율과 전경 이미지의 계산은 공유된 항을 재사용하기 위해 결합된다.

톤 매핑

입력 이미지의 알려지지 않은 톤 매핑을 보상하기 위해 삽입된 물체와 그림자에 적용되는 최적화 가능한 톤 보정 함수 $f(\cdot)$를 도입한다.

\[\begin{aligned} \hat{\textbf{I}}_\textrm{fg} &= f(\textbf{I}_\textrm{fg}; \boldsymbol{\theta}_\textrm{fg}) \\ \hat{\boldsymbol{\beta}}_\textrm{shadow} &= f(\boldsymbol{\beta}_\textrm{shadow}; \boldsymbol{\theta}_\textrm{shadow}) \end{aligned}\]

톤 커브는 여러 monotonic rational-quadratic spline을 사용한다. 이 스플라인은 $K_s = 5$개의 bin으로 구성되며 각각은 두 개의 이차 다항식의 몫으로 정의된다. 전경 이미지에 하나의 스플라인을 적용하고 그림자 비율의 각 RGB 채널에 대해 서로 다른 스플라인을 적용하여 그림자 색상을 조정할 수 있는 유연성을 제공한다.

미분 가능성

최종 출력 이미지는 전경 물체, 그림자, 배경 이미지의 알파 합성이다.

\[\begin{equation} \textbf{I}_\textrm{comp} = (1 - \textbf{V} (\mathcal{X})) \cdot \hat{\boldsymbol{\beta}}_\textrm{shadow} \cdot \textbf{I}_\textrm{bg} + \textbf{V} (\mathcal{X}) \hat{\textbf{I}}_\textrm{fg} \end{equation}\]

$\mathcal{X}$가 카메라에서 바로 보이면 $\textbf{V} (\mathcal{X})$는 1이고, 반대의 경우 0이다.

전경 렌더링, 그림자 렌더링, 또는 합성 연산이 물체 배치나 다른 불연속적인 양에 대한 미분을 필요로 하지 않기 때문에, 조명이나 재질 속성에 대한 pixelwise loss의 gradient를 얻기 위해 automatic differentiation을 사용할 수 있다. 이를 위해 Mitsuba 3의 Path Replay Backpropagation integrator를 사용한다. 최적화 가능한 파라미터는 조명 표현에 사용된 Spherical Gaussian 계수와 톤 곡선의 파라미터 \(\boldsymbol{\theta}_\textrm{fg}\), \(\boldsymbol{\theta}_\textrm{shadow}\)이다.

위의 각 연산은 secondary ray의 효과를 고려하지 않는 등 단순화가 포함되어 있지만, 저자들은 실제로 충분하다는 것을 확인했다. 시뮬레이션에서 남아 있는 불완전성은 조명 최적화를 통해 충분히 상쇄될 수 있다.

2. Diffusion Guidance

미분 가능한 렌더링 파이프라인에 의해 생성된 합성 이미지는 diffusion model에 대한 입력으로 사용되며, 이는 Score Distillation Sampling (SDS)과 유사한 최적화 목적 함수를 사용하여 guidance 신호를 계산하는 데 사용된다. 그러나 diffusion model은 본질적으로 조명에 대한 강력한 prior를 가지고 있지만, 저자들은 그것이 필요한 guidance를 즉시 제공하지 않는다는 것을 발견했다. 따라서 저자들은 특별히 설계된 적응형 score distillation loss를 제안하였다.

개념 보존을 통한 개인화

기존 diffusion model은 특히 야외 주행 환경과 같은 out-of-distribution 장면에서 가상 물체 삽입에 대한 강력한 guidance를 제공하지 않는 경우가 많다. 잠재적인 솔루션은 대상 장면의 이미지를 사용하여 diffusion model을 조정하는 것이다. 그러나 이 접근 방식은 종종 대상 장면의 콘텐츠에 너무 많은 overfitting을 초래하여 새로 삽입된 물체가 있는 장면에 모델이 적응하는 능력을 감소시킨다. 이로 인해 아티팩트와 불안정한 최적화 프로세스가 발생한다.

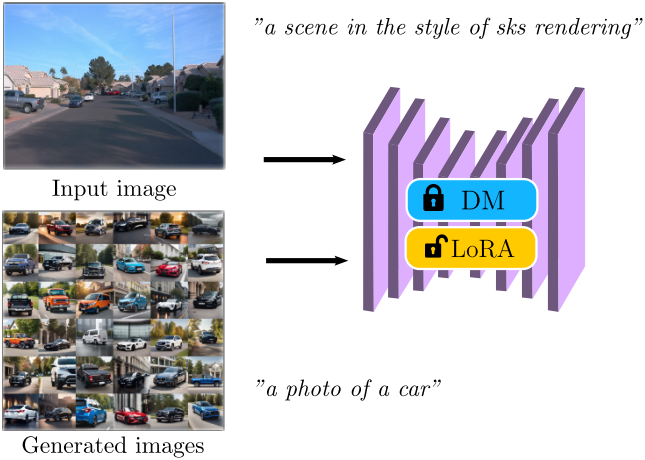
이 문제를 완화하기 위해, 삽입할 물체의 정체성을 보존하는 데 초점을 맞춰 diffusion model을 fine-tuning한다. 특히 저자들은 삽입 가능한 클래스 개념(ex. 자동차)에 대한 추가 합성 이미지를 생성하여 이를 달성했다. 저자들은 “a photo of a car”과 같은 기본 프롬프트에서 시작하여 색상, 배경, 조명, 크기와 같은 속성을 추가하여 생성된 데이터의 다양성을 보장하는 diffusion model에서 이러한 이미지를 샘플링하였다.

Diffusion model을 fine-tuning하기 위해 rank 4의 LoRA를 사용하여 타겟 예제를 이 보충 데이터와 결합한다. 학습은 다음과 같은 목적 함수를 따른다.

\[\begin{equation} \mathbb{E}_{\textbf{x} \sim p(\textbf{x}), \boldsymbol{\epsilon} \sim \mathcal{N}(\textbf{0}, \textbf{I}), t \sim T} [w(t) \| \boldsymbol{\epsilon_\theta} (\textbf{x}_t, t, \textbf{c}) - \boldsymbol{\epsilon} \|_2^2] \end{equation}\]

여기서 $\textbf{c}$는 두 개의 미리 정의된 프롬프트에 해당한다. 타겟 이미지는 “a scene in the style of sks rendering”을 사용하고, 생성된 이미지는 “a photo of a {concept class}”를 사용한다. “sks”는 개인화를 위한 특수 토큰이다. 실내 장면의 경우 약 30-40개의 보충 이미지를 샘플링하고 실외 장면의 경우 200개를 샘플링한다. Fine-tuning에 소요되는 총 시간은 일반적으로 하이엔드 GPU 하나에서 15분 미만이다.

적응형 guidance를 사용하는 score distillation

SDS는 사전 학습된 diffusion model을 활용하여 미분 가능한 이미지 렌더링 함수 \(g_\boldsymbol{\phi} := \textbf{x}\)의 최적화를 가이드한다. 파라미터 $\phi$는 Spherical Gaussian 조명과 톤 매핑 곡선의 파라미터에 해당하며, 다음과 같은 gradient를 사용하여 업데이트된다.

\[\begin{equation} \nabla_\boldsymbol{\phi} \mathcal{L}_\textrm{SDS} (\boldsymbol{\phi}, \boldsymbol{\theta}) := \mathbb{E}_{\boldsymbol{\epsilon} \sim \mathcal{N}(\textbf{0}, \textbf{I}), t \sim T} \bigg[ w(t) (\boldsymbol{\hat{\epsilon}_\theta} (\textbf{z}_t, t, \textbf{c}) - \boldsymbol{\epsilon}) \frac{\partial \textbf{z}_t}{\partial \boldsymbol{\phi}} \bigg] \\ \textrm{where} \; \textbf{z} = \mathcal{E} (g_\boldsymbol{\phi}), \; \hat{\boldsymbol{\epsilon_\theta}} (\textbf{z}_t, t, \textbf{c}) := (1 + s) \boldsymbol{\epsilon_\theta} (\textbf{z}_t, t, \textbf{c}) - s \boldsymbol{\epsilon_\theta} (\textbf{z}_t, t, \varnothing) \end{equation}\]

하지만 SDS loss를 본 논문의 문제에 적용할 때 학습이 불안정해진다. 따라서, 저자들은 LoRA 개인화를 통합하는 LDS loss를 제안하였다.

\[\begin{equation} \nabla_\boldsymbol{\phi} \mathcal{L}_\textrm{LDS} (\boldsymbol{\phi}, \boldsymbol{\theta}) := \mathbb{E}_{\boldsymbol{\epsilon} \sim \mathcal{N}(\textbf{0}, \textbf{I}), t \sim T} \bigg[ w(t) (\boldsymbol{\epsilon}_{(\boldsymbol{\theta} + \boldsymbol{\Delta \theta})} (\textbf{z}_t, t, \textbf{c}) - \boldsymbol{\epsilon_\theta} (\textbf{z}_t, t, \varnothing)) \frac{\partial \textbf{z}_t}{\partial \boldsymbol{\phi}} \bigg] \end{equation}\]

여기서 \(\boldsymbol{\epsilon}_{(\boldsymbol{\theta} + \boldsymbol{\Delta \theta})}\)는 LoRA로 개인화된 모델이 예측한 noise이다. 직관적으로 이 loss는 개인화된 모델이 결정한 방향으로 최적화 프로세스를 가이드하여 삽입된 물체의 개념을 보존하는 동시에 특정 장면의 외형과 semantic을 포착한다.

3. Optimization Formulation

Diffusion model의 개인화를 완료한 후 다음 loss function을 사용하여 조명 파라미터와 톤 매핑 파라미터를 최적화한다.

\[\begin{equation} \mathcal{L} = \mathcal{L}_\textrm{LDS} + \lambda_\textrm{consistency} \mathcal{L}_\textrm{consistency} + \lambda_\textrm{reg} \mathcal{L}_\textrm{reg} \end{equation}\]

텍스트 프롬프트로는 “a photo of a {concept class} in a scene in the style of sks rendering”을 사용한다. 여기서 “{concept class}”는 삽입할 물체의 컨텍스트를 제공하는 반면 개인화된 토큰 “sks”는 입력 이미지의 조명 스타일을 제공한다. \(\mathcal{L}_\textrm{LDS}\)는 편집된 이미지 \(\textbf{I}_\textrm{comp}\)에 적용되고 미분 가능한 렌더링 프로세스를 통해 최적화 가능한 파라미터로 역전파된다.

Environment map 초기화 및 융합

개인화된 diffusion model은 두 가지 방법으로 guidance를 제공한다.

1. 전경 물체와 장면의 조명 일관성을 장려한다. (삽입된 물체의 반사 및 크기 등)
2. 삽입된 물체가 배경 장면에 정확한 그림자를 드리우도록 장려한다. (그림자의 크기, 방향, 색상 등)

그러나 이 두 신호가 최적화 초기 단계에서 충돌할 수 있다.

이를 해결하기 위해 두 개의 별도 environment map \(\textbf{L}^\textrm{fg}, \textbf{L}^\textrm{shadow} \in \mathbb{R}^{H \times W \times 3}\)을 초기화하여 전경에 삽입된 물체를 비추고 각각 그림자를 만든다. 최적화가 진행됨에 따라 두 environment map은 점진적으로 하나의 environment map $\textbf{L}^\textrm{fused}$로 융합되며, 이는 \(\textbf{L}^\textrm{fg}\)와 \(\textbf{L}^\textrm{shadow}\) 사이의 상대적 휘도로 \(\textbf{L}^\textrm{fg}\)를 스케일링하여 융합된다.

또한 이 융합 프로세스에 다음 두 개의 정규화 항을 사용한다. 첫째, 다음을 최소화하여 environment map의 정규화된 휘도 \(\tilde{\textbf{L}}^\textrm{fg}, \tilde{\textbf{L}}^\textrm{shadow} \in \mathbb{R}^{H \times W \times 3}\) 간의 일관성을 장려한다.

\[\begin{equation} \mathcal{L}_\textrm{consistency} = - \sum_{i,j} \tilde{\textbf{L}}_{i,j}^\textrm{shadow} \log (\tilde{\textbf{L}}_{i,j}^\textrm{fg}) \Delta \Omega_{i,j} \end{equation}\]

여기서 \(\Delta \Omega_{i,j}\)는 픽셀 $(i, j)$에 대한 입체각이고 \(\tilde{\textbf{L}}^\textrm{shadow}\)의 gradient는 detach된다.

둘째, 그림자 environment map \(\textbf{L}^\textrm{shadow}\)는 주로 그림자 비율 \(\boldsymbol{\beta}_\textrm{shadow} \in \mathbb{R}^{H \times W \times 3}\)을 통해 학습되므로 선명한 그림자에 대한 집중된 높은 피크를 장려하고 \(\textbf{L}^\textrm{shadow}\)의 주변광을 억제하기 위해 Cauchy loss를 사용한 log space에서의 L2 regularizer를 추가한다.

\[\begin{equation} \mathcal{L}_\textrm{reg} = \sum_{i,j,c} \log (1 + 2 (\textbf{L}_{i,j,c}^\textrm{shadow})^2) \Delta \Omega_{i,j} \end{equation}\]

Experiments

• 데이터셋: Waymo, PolyHaven

1. Evaluation on Benchmark Datasets

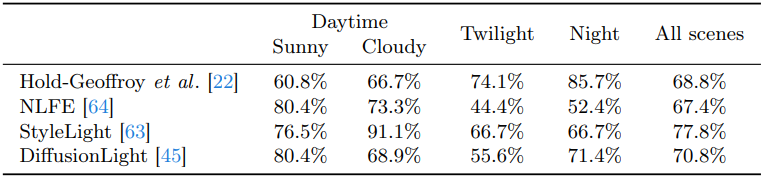
다음은 Waymo의 장면들에서 다른 방법들과 비교한 결과이다.

다음은 PolyHaven의 장면들에서 다른 방법들과 비교한 결과이다.

2. Ablation Study

다음은 야외 운전 장면에서의 ablation 결과이다.

3. Applications

다음은 물리 기반 렌더링 파이프라인을 활용하여 재료, 헤드라이트, 톤 매핑과 같은 다른 장면 속성을 최적화한 예시이다.

Limitations

1. Spherical Gaussian 기반 조명 표현은 일반 물체에는 적합하지만, 매우 반사적인 재료에는 사실적으로 작동하지 않을 수 있다.
2. 렌더링 공식은 장면 자체에서 삽입된 물체로의 반사와 같은 효과를 설명하도록 확장될 수 있지만, 더 많은 모호성을 도입하고 proxy geometry의 재료를 알아야 할 수 있다.
3. Diffusion model 개인화는 결과의 품질을 크게 개선하지만 파이프라인에 오버헤드와 복잡성을 추가한다.