[논문리뷰] Dilated Neighborhood Attention Transformer (DiNAT)
arXiv 2022. [Paper] [Github]
Ali Hassani, Humphrey Shi
SHI Labs | Picsart AI Research (PAIR)
29 Sep 2022
Introduction
Transformer는 self attention을 기반으로 구축된 범용 아키텍처 덕분에 음성 및 비전과 같은 다른 modality에 적용되기 전에 자연어 이해에서 시작하여 AI 연구에 상당한 기여를 했다. ViT는 비전의 사실상의 표준인 CNN에 대한 직접적인 대안으로서 transformer의 첫 번째 주요 시연 중 하나였다. ViT는 이미지를 일련의 패치로 취급하고 일반 transformer 인코더를 사용하여 이미지를 인코딩하고 분류한다. 대규모 이미지 분류에서 CNN과의 경쟁력 있는 성능을 보여주었으며, CNN과의 경쟁으로 transformer 기반 아키텍처에 초점을 맞춘 비전 연구가 급증하는 결과를 낳았다.
ViT와 CNN은 아키텍처와 빌딩 블록 측면에서 뿐만 아니라 데이터를 처리하는 방식에서도 다르다. CNN은 일반적으로 입력이 모델을 통과하고 계층적 feature map을 구성할 때 점진적으로 입력을 다운샘플링한다. 객체의 스케일이 다양하고 고해상도 feature map은 segmentation과 같은 dense task에 중요하기 때문에 이 계층적 디자인은 비전에 중요하다. 반면에 transformer는 모델 전체에서 고정된 차원으로 알려져 있으며, 그 결과 일반 ViT는 처음부터 공격적으로 입력을 다운샘플링하여 self attention의 2차 비용을 완화하므로 일반 ViT를 dense task의 backbone으로 적용하는 것을 방해한다.
일반 ViT를 dense task에 적용하는 연구가 계속되는 동안 계층적 ViT에 대한 연구는 빠르게 우세해졌으며 계속 성장하고 있다. 이러한 계층적 transformer 모델의 주요 이점은 기존 계층적 비전 프레임워크와의 통합 용이성이다. 기존 CNN에서 영감을 받은 계층적 ViT는 중간에 다운샘플링 모듈이 있고 덜 공격적인 초기 다운샘플링이 있는 여러 레벨의 transformer 인코더로 구성된다. 계층적 transformer의 이전 레이어는 제한되지 않은 self attention을 사용하는 경우 입력 해상도에 대해 2차적으로 증가하는 복잡도와 메모리 사용량을 부담하여 고해상도 이미지에 대해 다루기 어렵다. 따라서 계층적 transformer는 일반적으로 특정 로컬 attention 메커니즘을 사용한다.
가장 초기의 계층적 ViT 중 하나인 Swin Transformer는 window self attention (WSA) 모듈과 shifted window self attention (SWSA) 모듈을 사용한다. 둘 다 self attention을 겹치지 않는 하위 창으로 localize한다. 이는 self attention 비용을 줄여 해상도와 대해 시간 및 공간 복잡도를 선형으로 만든다. SWSA는 WSA와 동일하지만, 그 앞에 feature map 픽셀이 이동하고 뒤이어 역 이동이 뒤따른다. 이것은 window 밖의 상호작용을 허용하고 따라서 receptive field의 확장을 허용하므로 성능에 필수적이다. Swin의 주요 이점 중 하나는 효율성이다. 픽셀 이동과 window 분할은 상대적으로 저렴하고 쉽게 병렬화할 수 있는 연산이기 때문이다. 또한 self attention을 거의 또는 전혀 변경하지 않으므로 구현이 더 쉬워진다. Swin은 여러 비전 task에서 SOTA가 되었으며 대규모 사전 학습을 수용하기 위해 Swin-V2가 그 뒤를 이었다.
Neighborhood Attention Transformer (NAT)는 간단한 sliding-window 기반 attention인 Neighborhood Attention (NA)과 함께 소개되었다. Convolution 스타일로 attend하는 Stand Alone Self Attention (SASA)와 달리 NA는 각 토큰 주변의 nearest neighbor에 self attention을 국한하므로 정의에 따라 self attention에 접근하고 고정된 attention span을 가진다. 이러한 픽셀별 attention 연산은 Neighborhood Attention Extension이 릴리스될 때까지 비효율적이고 병렬화하기 어려운 것으로 간주되었다. 이 extension을 통해 NA는 실제로 Swin의 SWSA보다 훨씬 빠르게 실행할 수 있다. NAT는 이미지 분류에서 Swin을 훨씬 능가할 수 있었고 다운스트림 task에서 경쟁력 있는 성능을 달성하는 동시에 약간 다른 아키텍처에도 불구하고 Swin보다 더 빠르게 확장할 수 있었다.
로컬 attention을 가진 계층적 ViT에 대한 노력에도 불구하고, 글로벌 receptive field와 장거리 상호 의존성을 모델링하는 능력을 포함하여 self attention의 가장 중요한 속성 중 일부는 이러한 localization의 결과로 약화된다. 이것은 간단한 질문으로 이어진다.
로컬 attention이 계층적 ViT에서 제공하는 다루기 쉬움을 유지하면서 단점을 피하는 방법은 무엇인가?
즉, 최적의 시나리오는 선형 복잡도를 유지하면서 글로벌 receptive field와 self attention의 장거리 상호 의존성을 모델링하는 능력을 유지하는 것이다. 본 논문에서는 간단한 로컬 attention 메커니즘인 NA를 Dilated Neighborhood Attention (DiNA)로 확장하여 이 질문에 답하고 계층적 transformer를 개선하는 것을 목표로 한다. NA의 neighborhood를 더 큰 희소 영역으로 확장하면 여러 가지 이점이 있다.
- 더 많은 글로벌 컨텍스트를 캡처한다.
- Receptive field가 선형이 아닌 지수적으로 증가할 수 있다.
- 추가 계산 비용이 없다.
본 논문은 DiNA의 효율성을 입증하기 위해 Dilated Neighborhood Attention Transformer (DiNAT)를 제안한다. DiNAT는 다운스트림 성능 측면에서 기존 NAT 모델을 개선할 뿐만 아니라 눈에 띄는 성능 차이로 다운스트림 task에서 ConvNeXt와 같은 강력한 최신 CNN 기준선을 능가한다.
Method
1. Dilated Neighborhood Attention
단순화를 위해 표기법을 단일 차원 NA와 DiNA로 제한한다. 행이 $d$차원 토큰 벡터인 입력 행렬 $X \in \mathbb{R}^{n \times d}$, $X$의 linear projection $Q$, $K$, $V$, 상대 위치 바이어스 $B(i, j)$가 주어지면, neighborhood 크기 $k$와 $i$번째 입력에 대하여 $i$번째 입력의 query projection과 $k$개의 nearest neighboring key projection의 내적으로 attention 가중치 $A_i^k$를 정의한다.
\[\begin{equation} A_i^k = \begin{bmatrix} Q_i K_{\rho_1 (i)}^\top + B_{(i, \rho_1 (i))} \\ Q_i K_{\rho_2 (i)}^\top + B_{(i, \rho_2 (i))} \\ \vdots \\ Q_i K_{\rho_k (i)}^\top + B_{(i, \rho_k (i))} \end{bmatrix} \end{equation}\]여기서 $\rho_j (i)$는 $i$의 $j$번째 nearest neighbor을 나타낸다. 그런 다음 neighboring value $V_i^k$를 행이 $i$번째 입력의 $k$번째 nearest neighboring value projection인 행렬로 정의한다.
\[\begin{equation} V_i^k = [V_{\rho_1 (i)}^\top \; V_{\rho_2 (i)}^\top \; \cdot \; V_{\rho_k (i)}^\top ]^\top \end{equation}\]여기서 $V$는 $X$의 linear projection이다. Neighborhood 크기가 $k$인 $i$번째 토큰에 대한 Neighborhood Attention은 다음과 같이 정의된다.
\[\begin{equation} \textrm{NA}_k (i) = \textrm{softmax} \bigg(\frac{A_i^k}{\sqrt{d}}\bigg) V_i^k \end{equation}\]여기서 $\sqrt{d}$는 스케일링 파라미터이고 $d$는 임베딩 차원이다.
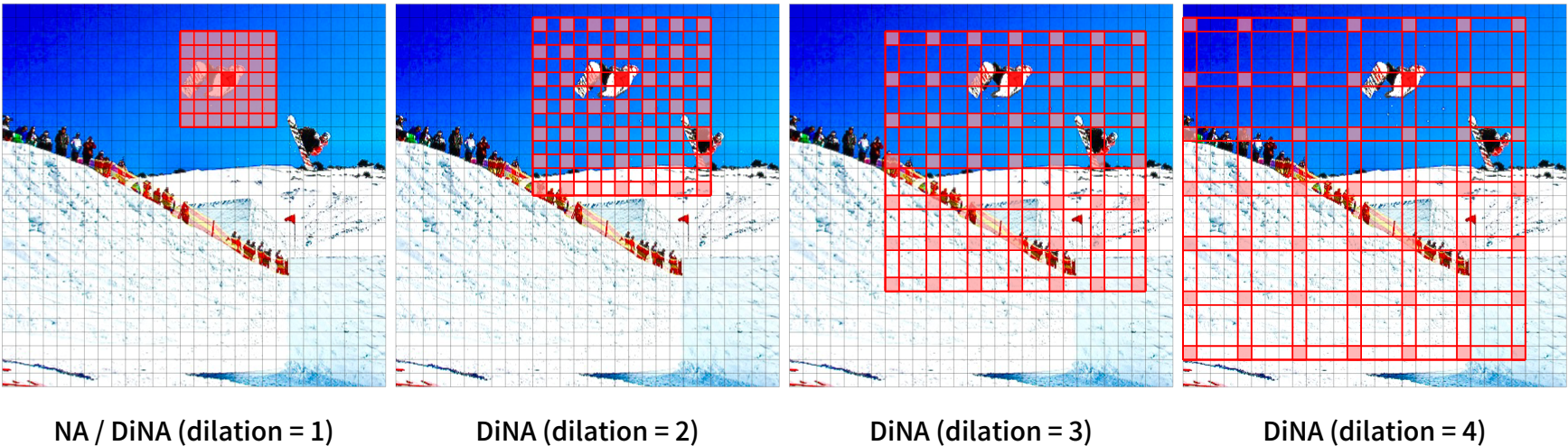
이 정의를 DiNA로 확장하기 위해 dilation 값 $\delta$가 주어지면 $\rho_j^\delta (i)$를 $j \textrm{mod} \delta = i \textrm{mod} \delta$를 충족하는 토큰 $i$의 $j$번째 nearest neighbor로 정의한다. 그런 다음 다음과 같이 neighborhood 크기가 $k$인 $i$번째 토큰에 대한 $\delta$-dilated neighborhood attention 가중치 $A_i^{(k, \delta)}$를 정의할 수 있다.
\[\begin{equation} A_i^{(k, \delta)} = \begin{bmatrix} Q_i K_{\rho_1^\delta (i)}^\top + B_{(i, \rho_1^\delta (i))} \\ Q_i K_{\rho_2^\delta (i)}^\top + B_{(i, \rho_2^\delta (i))} \\ \vdots \\ Q_i K_{\rho_k^\delta (i)}^\top + B_{(i, \rho_k^\delta (i))} \end{bmatrix} \end{equation}\]Neighborhood 크기가 $k$인 $i$번째 토큰에 대해 $\delta$-dilated neighboring value를 비슷하게 정의한다.
\[\begin{equation} V_i^{(k, \delta)} = [V_{\rho_1^\delta (i)}^\top \; V_{\rho_2^\delta (i)}^\top \; \cdot \; V_{\rho_k^\delta (i)}^\top ]^\top \end{equation}\]Neighborhood 크기가 $k$인 $i$번째 토큰에 대해 DiNA 출력은 다음과 같이 정의된다.
\[\begin{equation} \textrm{DiNA}_k^\delta (i) = \textrm{softmax} \bigg(\frac{A_i^{(k, \delta)}}{\sqrt{d_k}}\bigg) V_i^{(k, \delta)} \end{equation}\]2. Choice of Dilation
DiNA는 새로운 핵심 아키텍처 하이퍼파라미터인 레이어별 dilation 값을 도입했다. Dilation 값의 상한을 $\lfloor \frac{n}{k} \rfloor$로 정의한다. 여기서 $n$은 토큰 수이고 $k$는 커널/neighborhood 크기이다. 이것은 단순히 각 토큰에 대해 정확히 $k$개의 dilated neighbor이 존재하도록 하기 위한 것이다. 하한은 항상 1이며 NA와 동일하다. 따라서 모델의 각 레이어의 dilation 값은 정수 $\delta \in [1, \lfloor \frac{n}{k} \rfloor]$를 취할 수 있는 입력 의존 hyperparameter가 된다. Dilation 값은 변경 가능하기 때문에 유연한 receptive field를 제공한다. 가능한 모든 조합을 시도하는 것은 불가능하므로 저자들은 제한된 수의 선택을 탐색했다.
3. Receptive Fields
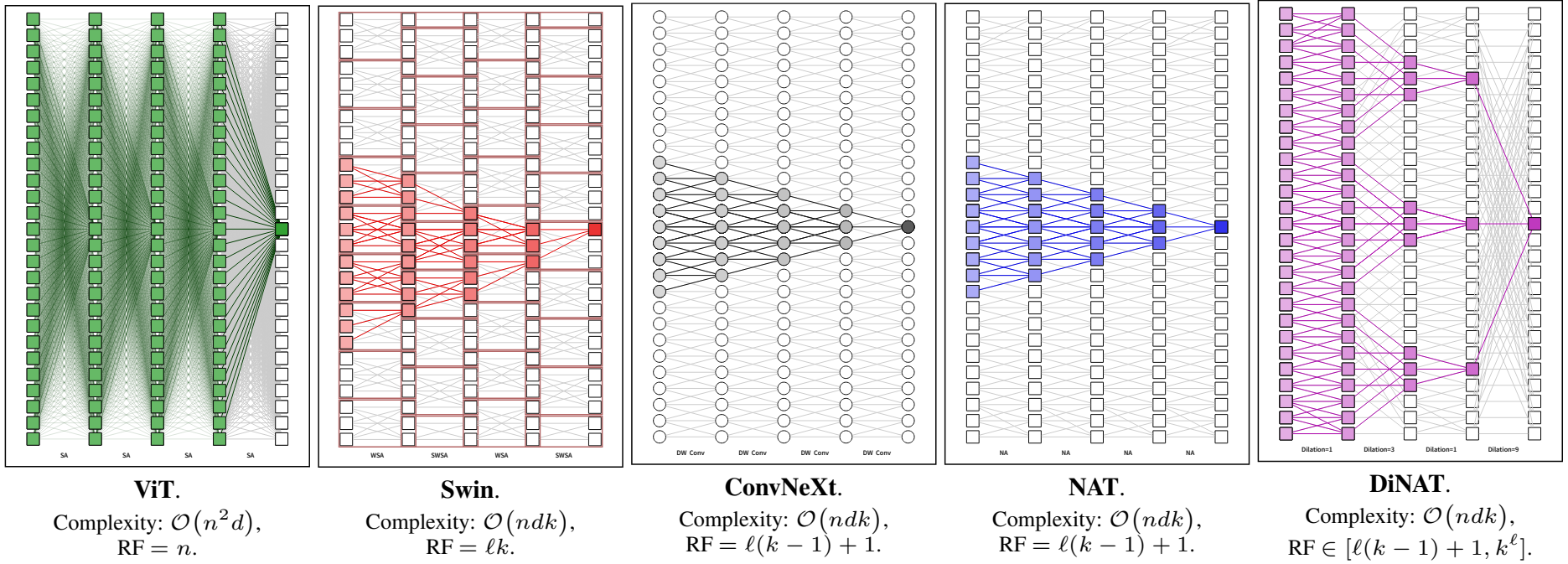
저자들은 특히 다른 모델과 비교하여 DiNA의 힘을 이해하는 것이 중요하므로 DiNA의 receptive field를 분석하였다. 아래 표는 FLOPs, 메모리 사용과 다양한 attention 패턴에서 receptive field 크기를 비교한 것이다. 또한 완전성을 위해 ConvNeXt의 핵심 구성 요소인 nclude depth-wise separable convol (DWSConv)을 포함한다.

여기서 $\ell$은 레이어 수, $k$는 커널 크기, $n$은 토큰 수이다.
Convolution과 NA 모두 크기 $k$의 receptive field로 시작하여 레이어당 $k - 1$씩 확장한다 (가운데 픽셀은 고정된 상태로 유지됨). Swin Transformer의 WSA는 자체적으로 일정한 receptive field를 유지한다. Window 분할이 window 간 상호 작용을 막아 receptive field 확장을 막기 때문이다. SWSA는 이 문제를 해결하고 레이어당 정확히 하나의 window (레이어당 $k$의 dilation)만큼 receptive field를 확장한다.
Swin은 특수 shifted window 디자인 덕분에 NAT와 ConvNeXt에 비해 약간 더 큰 receptive field를 가지지만 대칭이라는 중요한 속성을 깨뜨린다. Swin의 feature map은 겹치지 않는 window로 분할되기 때문에 동일한 window 내의 픽셀은 위치에 관계없이 서로에게만 attend하므로 일부 픽셀은 주변의 비대칭 컨텍스트를 보게 된다.
NAT, Swin, ConvNeXt의 고정된 receptive field 성장과 달리 DiNA의 receptive field는 유연하며 dilation에 따라 변경된다. 그것은 NAT의 원래 $\ell(k − 1) + 1$ (모든 dilation 값이 1로 설정됨)에서 기하급수적으로 증가하는 receptive field인 $k^\ell$ (점진적 dilation 증가)에 이르기까지 다양할 수 있으며 이것이 그 힘의 주된 이유 중 하나이다. Dilation에 관계없이 첫 번째 레이어는 항상 크기 $k$의 receptive field를 생성한다. Dilation 값이 충분히 크면 이전 DiNA 레이어는 DiNA 레이어의 각 $k$에 대해 크기 $k$의 receptive field를 생성하여 크기가 $k^2$인 receptive field를 생성한다. 결과적으로 최적의 dilation 값을 가진 DiNA 및 NA 조합은 잠재적으로 receptive field를 $k^\ell$로 기하급수적으로 증가시킬 수 있다. Dilated convolution은 기하급수적으로 증가하는 dilation 값을 사용할 때 receptive field 크기가 기하급수적으로 증가하는 것으로 알려져 있기 때문에 이것은 놀라운 일이 아니다. 증가된 receptive field 크기의 그림은 아래 그림에 나와 있다.
4. DiNAT
저자들은 DiNA의 성능을 공정하게 평가하기 위해 아키텍처 및 구성 측면에서 DiNAT을 원래 NAT 모델과 동일하게 설계했다. 초기에 2$\times$2 stride가 있는 2개의 3$\times$3 convolution layer를 사용하여 입력 해상도의 $1/4$인 feature map을 생성한다. 또한 2$\times$2 stride의 단일 3$\times$3 convolution을 사용하여 레벨 간 다운샘플링을 수행하여 공간 해상도를 절반으로 줄이고 채널을 두 배로 늘린다. 자세한 내용은 아래 표에 나와 있다.
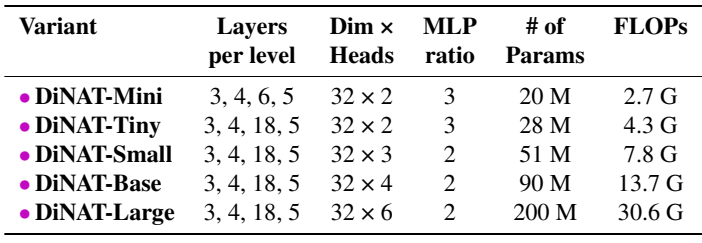
DiNAT의 주요 차이점은 다른 모든 레이어가 NA 대신 DiNA를 사용한다는 것이다. DiNA 레이어의 dilation 값은 task와 입력 해상도를 기반으로 설정된다. $224^2$ 해상도의 ImageNet-1k의 경우 dilation 값을 레벨 1에서 4까지 각각 8, 4, 2, 1로 설정한다. 다운스트림 task에서는 해상도가 더 크기 때문에 dilation 값을 그 이상으로 늘린다.
5. Implementation
기존 Neighborhood Attention Extension ($\mathcal{N}$ATTEN) 위에 DiNA를 구현하여 사용 편의성과 NA와 동일한 메모리 사용을 허용했다. Extension의 최신 공개 버전에는 속도 측면에서 Swin과 같은 방법과 경쟁할 수 있는 Neighborhood Attention의 보다 효율적인 “tiled” 구현이 포함되어 있다. 기존의 모든 CUDA 커널에 dilation 요소를 추가하고 확장된 메모리 형식을 지원하도록 “tiled” 커널을 다시 구현함으로써 기존 NA 커널의 속도에 영향을 주지 않고 DiNA를 구현할 수 있었다. 그러나 DiNA의 처리량은 dilation 값에 따라 달라지며 실제로는 NA보다 약간 느릴 것으로 예상된다. 이것은 단순히 메모리 액세스 패턴의 중단으로 인한 것이며 전체 처리량에 영향을 미친다. 또한 이러한 구현은 여전히 순진하고 Tensor Core와 같은 CUDA의 최신 아키텍처 표준을 완전히 활용하지 않으므로 개념 증명으로만 작동한다. 이러한 제한에도 불구하고 NA와 DiNA를 사용하는 모델은 convolution, linear projection, self attention을 주로 활용하는 다른 방법에 비해 경쟁력 있는 처리량 수준을 달성할 수 있다.
Experiments
1. Image Classification
다음은 ImageNet-1K $224^2$에서 이미지 분류 성능을 비교한 표이다.
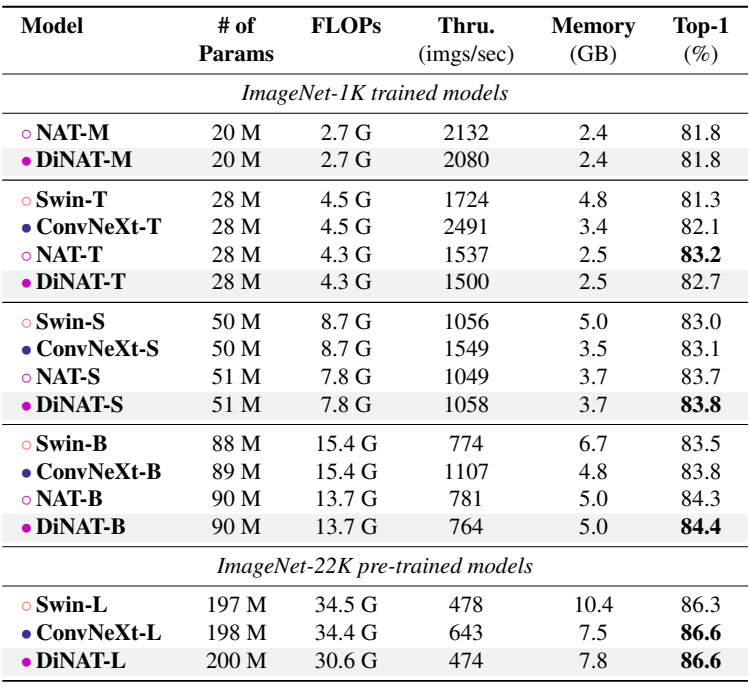
다음은 ImageNet-1K $384^2$에서 이미지 분류 성능을 비교한 표이다.
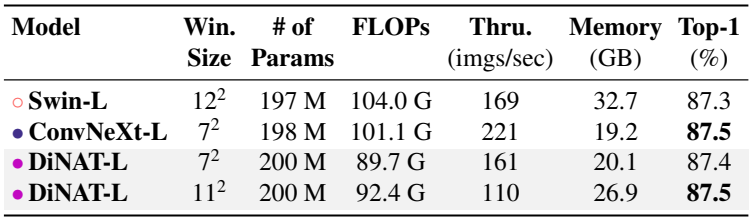
다음은 ImageNet-1K에서 Top-1 accuracy를 비교한 표이다.
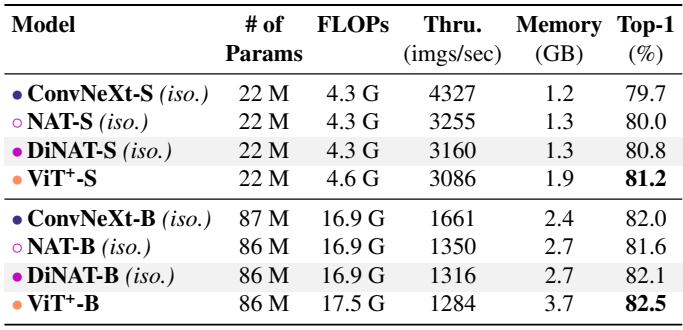
다음은 다양한 레이어 구조에 대한 성능을 비교한 표이다.
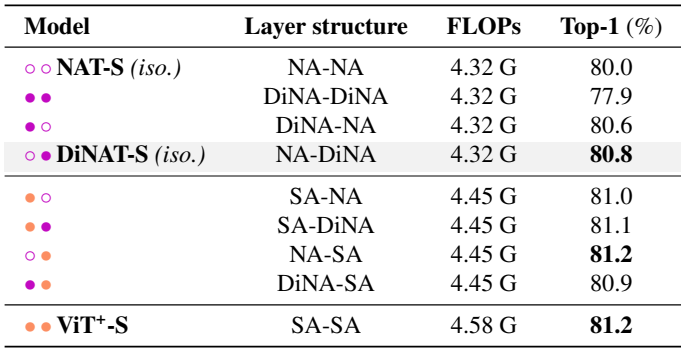
2. Object Detection and Instance Segmentation
다음은 COCO object detection과 instance segmentation 성능이다.
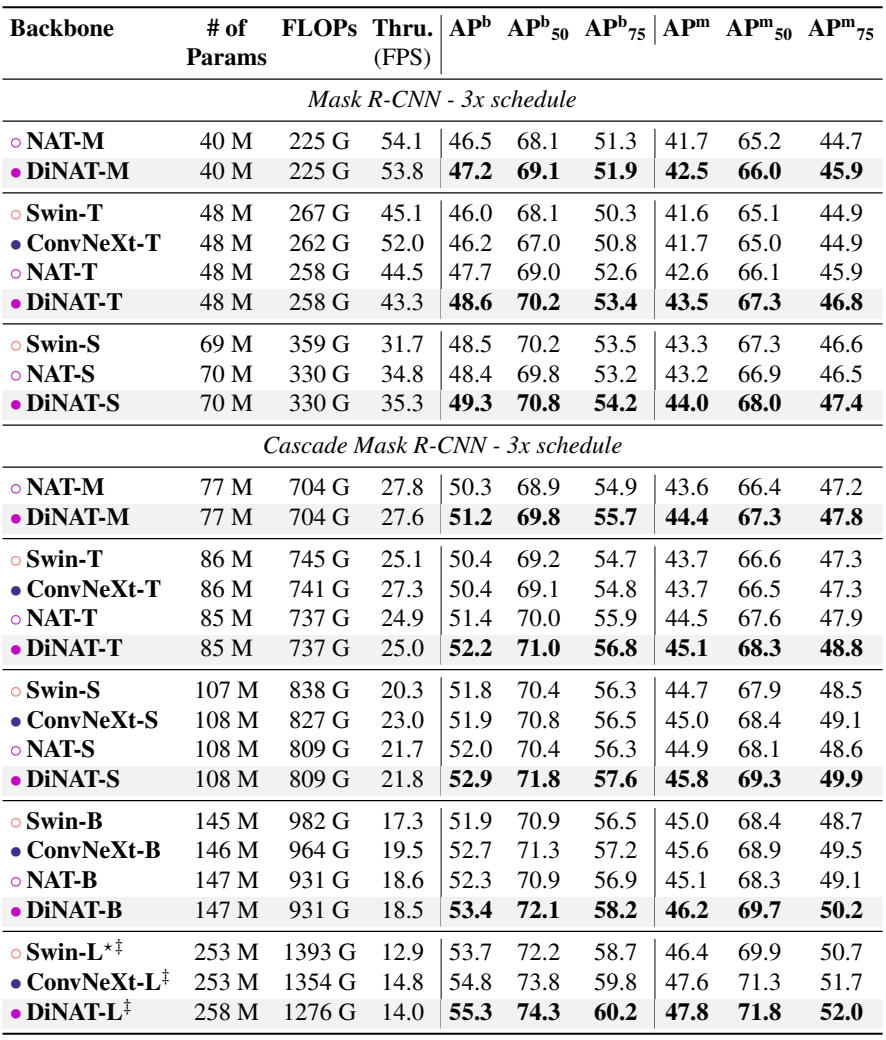
3. Semantic Segmentation
다음은 ADE20K semantic segmentation 성능이다.
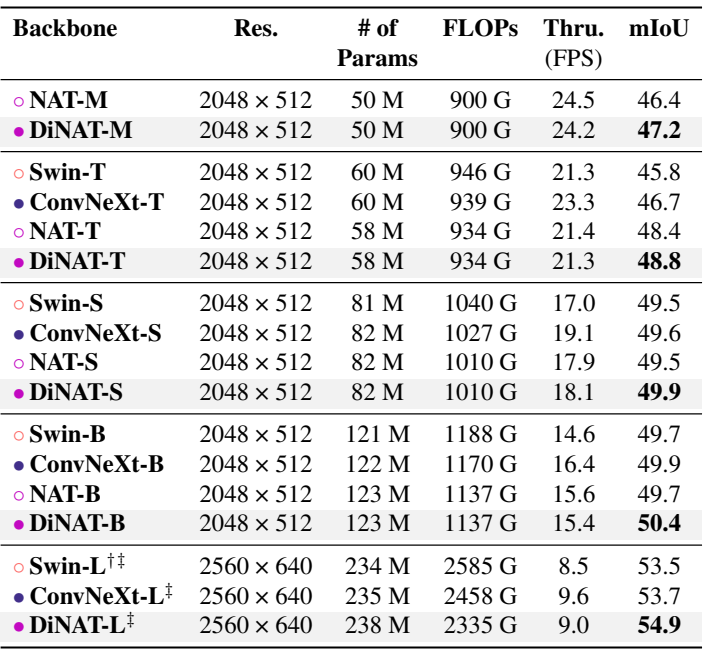
4. Ablation study
다음은 dilation에 따른 성능을 비교한 표이다.

다음은 레이어 구조에 따른 성능을 비교한 표이다.
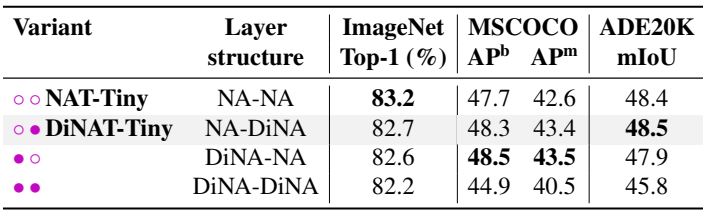
다음은 커널 크기에 따른 성능을 비교한 표이다.
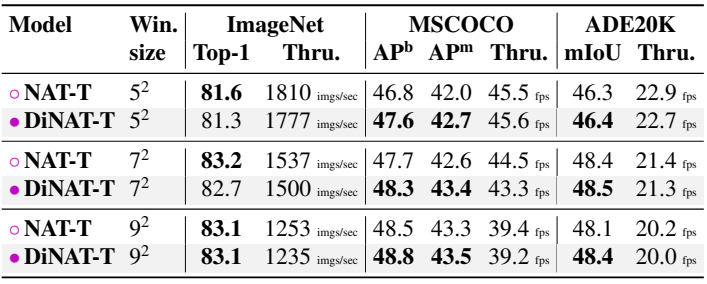
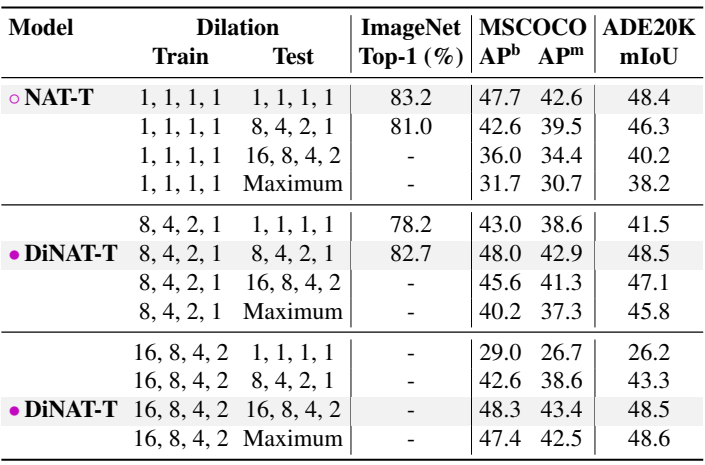
다음은 테스트 시의 dilation 변경에 따른 성능을 비교한 표이다.
5. Image segmentation with Mask2Former
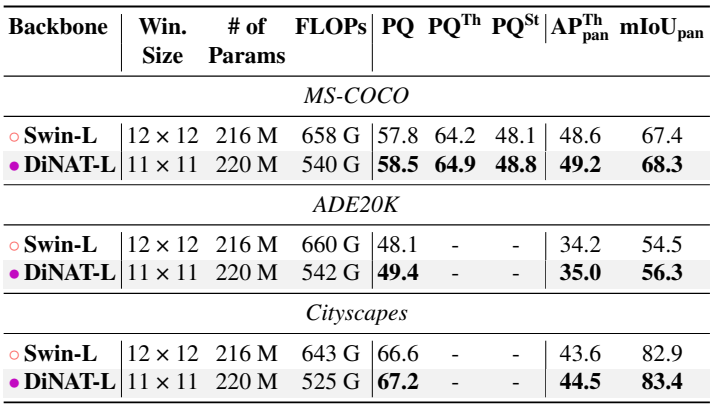
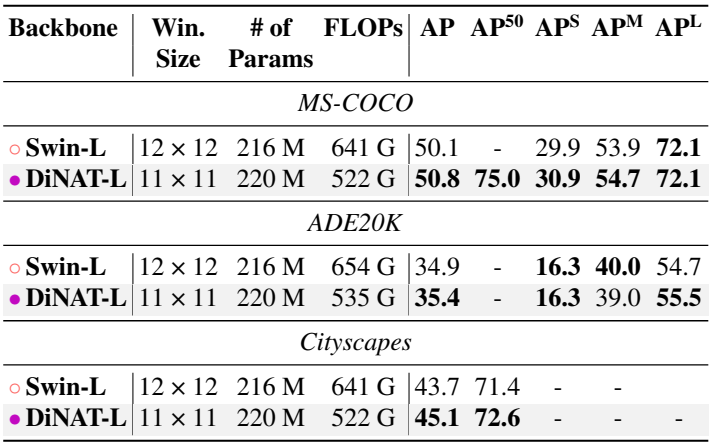
다음은 Mask2Former를 사용한 instance segmentation 성능을 비교한 표이다.
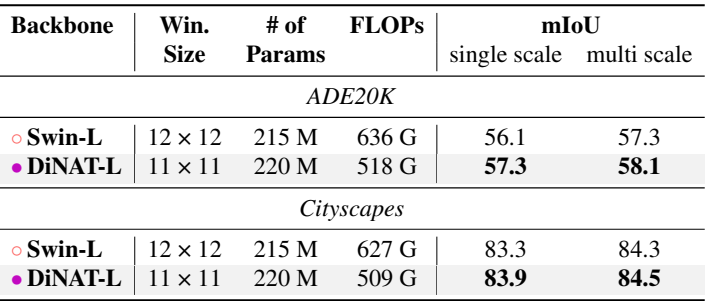
다음은 Mask2Former를 사용한 semantic segmentation 성능을 비교한 표이다.
다음은 Mask2Former를 사용한 panoptic segmentation 성능을 비교한 표이다.