[논문리뷰] DiffusionSfM: Predicting Structure and Motion via Ray Origin and Endpoint Diffusion

CVPR 2025. [Paper] [Page] [Github]
Qitao Zhao, Amy Lin, Jeff Tan, Jason Y. Zhang, Deva Ramanan, Shubham Tulsiani
Carnegie Mellon University
8 May 2025

Introduction

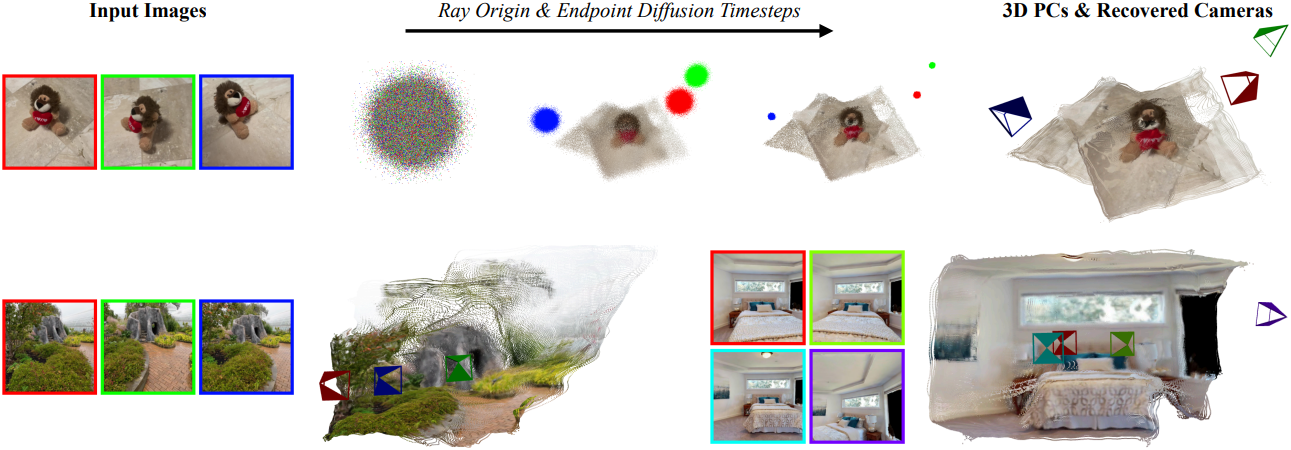
본 논문에서는 여러 입력 이미지에서 dense한 3D 형상과 카메라 포즈를 직접 추론하는 end-to-end 멀티뷰 모델인 DiffusionSfM을 제시하였다. RayDiffusion은 이미지 패치별 광선을 예측하고, DUSt3R는 픽셀별 3D 포인트를 추론한다. DiffusionSfM은 두 가지를 효과적으로 결합하여 픽셀별로 광선 원점과 끝점을 예측하고, 장면 형상(끝점)과 카메라(광선)를 모두 직접 얻는다.

RayDiffusion과 비교하여, DiffusionSfM은 더 세밀한 규모에서 구조와 카메라 포즈를 직접 예측한다 (픽셀 단위 vs. 패치 단위). DiffusionSfM은 구조와 카메라 포즈를 $N$개 뷰에 대해 직접 예측하기 때문에, DUSt3R와 달리 메모리 집약적인 글로벌 정렬이 필요 없다. 불확실성을 모델링하기 위해 diffusion model을 사용하며, 해결해야 할 두 가지 주요 과제가 있다.

1. Diffusion model은 학습을 위한 입력으로 GT 데이터가 필요하지만, 기존 현실 데이터셋은 깊이 정보가 누락되어 모든 픽셀에 대한 끝점을 가지고 있지 않다.
2. 끝점의 3D 좌표는 잠재적으로 무한할 수 있는 반면, diffusion model은 정규화된 데이터가 필요하다.

이러한 문제를 극복하기 위해, 저자들은 추가적인 GT 마스크 컨디셔닝을 입력으로 활용하여 모델에 누락된 입력 데이터를 알리고, 유클리드 공간 대신 ​projective space에서 3D 포인트를 parameterize한다. 이러한 전략을 통해 구조와 카메라 포즈에 대한 정확한 예측을 학습할 수 있다.

DiffusionSfM은 물체 중심 이미지와 장면 수준 이미지 모두에 대해 정확한 형상과 카메라를 추론할 수 있다. 특히, 기존 방법들보다 더 정확한 카메라 추정값을 제공하는 동시에 diffusion process를 통해 불확실성을 모델링한다.

Method

1. 3D Scenes as Ray Origins and Endpoints

입력 이미지 $\textbf{I} \in \mathbb{R}^{H \times W \times 3}$의 depth map \(\textbf{D} \in \mathbb{R}^{H \times W}\), 카메라 intrinsic \(\textbf{K} \in \mathbb{R}^{3 \times 3}\), world-to-camera extrinsic \(\textbf{T} \in \mathbb{R}^{4 \times 4}\) (rotation $\textbf{R} \in \textrm{SO}(3)$, translation $\textbf{t} \in \mathbb{R}^3$)가 주어졌을 때, 각 2D 이미지 픽셀 \(\textbf{P}_{ij} = [u, v]\)는 카메라 중심 $\textbf{c}$에서 시작하여 이미지 평면을 통과하고 depth map $\textbf{D}$에 따라 지정된 물체 표면에서 끝나는 광선에 해당한다. 이미지 픽셀 \(\textbf{P}_{ij}\)에 대한 광선의 끝점은 다음과 같다.

\[\begin{equation} \textbf{E}_{ij} = \textbf{T}^{-1} h (\textbf{D}_{ij} \cdot \textbf{K}^{-1} [u,v,1]^\top) \end{equation}\]

($h$는 3D 포인트를 homogeneous coordinate으로 매핑)

모든 픽셀에 대한 광선 원점 \(\textbf{O}_{ij}\)는 카메라 중심 $\textbf{c}$와 동일하다.

\[\begin{equation} \textbf{O}_{ij} = \textbf{c} = h (- \textbf{R}^{-1} \textbf{t}) \end{equation}\]

각 이미지 픽셀은 world coordinate에서의 카메라의 위치와 물체 표면에서 관측된 3D 포인트를 나타내는 광선 원점과 끝점 \(\textbf{S}_{ij} = \langle \textbf{O}_{ij}, \textbf{E}_{ij} \rangle\)과 연결된다. 광선 원점과 끝점의 묶음이 주어지면 해당 카메라 포즈를 쉽게 추출할 수 있다.

과도하게 parameterize된 표현

본 논문은 quaternion이나 translation 벡터 대신, 분산된 광선 원점 $\textbf{O}$와 끝점 $\textbf{E}$를 사용하여 3D 장면과 카메라를 표현한다. 이 디자인은 RayDiffusion에서 영감을 받았으며, DINOv2와 같은 SOTA 비전 백본의 feature를 사용하여 이미지 정보를 패치 방식으로 인코딩하는 것을 용이하게 한다. 특히, 광선 원점 $\textbf{O}$는 모든 픽셀에서 동일해야 하지만, 광선 끝점 $\textbf{E}$를 따라 dense하게 $\textbf{O}$를 예측한다. 이를 통해 광선 원점이 동일한 이미지 내에서 가깝게 유지되도록 하여 학습 중에 암시적인 정규화를 제공한다. 실제로 광선 원점과 끝점을 동시에 예측하는 것은 하나의 projection head를 사용하여 쉽게 구현할 수 있다.

2. DiffusionSfM

Diffusion 프레임워크

$N$개의 입력 이미지 집합과 연관된 픽셀 정렬된 광선 원점과 끝점 \(\mathcal{S} = \textrm{stack}(\{\textbf{S}^{(n)}\}_{n=1}^N)\)이 주어지면, 시간에 따른 Gaussian noise를 추가하는 forward diffusion process를 적용하여 \(\mathcal{S}_t\)를 얻는다. \(\mathcal{S}_0\)는 noise가 추가되지 않은 깨끗한 샘플이고, \(\mathcal{S}_T\)는 순수 Gaussian noise이다. Forward diffusion process는 다음과 같이 정의된다.

\[\begin{equation} \mathcal{S}_t = \sqrt{\vphantom{1} \bar{\alpha}_t} \mathcal{S}_0 + \sqrt{1 - \bar{\alpha}_t} \epsilon \\ \textrm{where} \quad t \sim \textrm{Uniform}(0, T], \; \epsilon \sim \mathcal{N}(0, I) \end{equation}\]

\(\bar{\alpha}_t\)는 각 timestep에서 추가되는 noise의 강도를 제어한다. Diffusion model $f_\theta$는 다음 loss function을 사용하여 학습된다.

\[\begin{equation} \mathcal{L}_\textrm{Diffusion} = \mathbb{E}_{t, \mathcal{S}_0, \epsilon} \| \mathcal{S}_0 - f_\theta (\mathcal{S}_t, t, \mathcal{C}) \|^2 \end{equation}\]

아키텍처

저자들은 DINOv2의 이미지 feature \(\mathcal{C} \in \mathbb{R}^{N \times h \times w \times c_1}\)을 조건으로 하는 DiT 아키텍처를 사용하여 $f_\theta$를 구현하였다. DINOv2에서 학습한 공간 정보에 맞춰 픽셀을 정렬하기 위해, \(\mathcal{S}_t\)에 convolutional layer를 적용하여 공간적으로 다운샘플링하고 feature 차원을 증가시킨다.

\[\begin{equation} \mathcal{F} = \textrm{Conv} (\mathcal{S}_t) \in \mathbb{R}^{N \times h \times w \times c_2} \end{equation}\]

결합된 DiT 입력은 채널 차원을 따라 두 feature 집합을 concat하여 $\mathcal{F} \oplus \mathcal{C}$로 구성된다. DiT 내에서 패치별 feature 집합은 self-attention을 통해 다른 feature 집합에 attention된다. 서로 다른 이미지와 패치를 구분하기 위해 이미지 및 패치 인덱스를 기반으로 sinusoidal positional encoding을 적용한다.

DiT는 저해상도 feature를 처리하는 반면, 본 논문의 목표는 dense한 광선 원점과 끝점을 생성하는 것이다. 이를 위해 DINOv2와 DiT의 중간 feature map을 입력으로 받는 DPT 디코더를 사용한다. DPT 디코더는 여러 convolutional layer들을 통해 feature 해상도를 점진적으로 높인다. 최종 광선 원점과 끝점은 하나의 linear layer를 사용하여 DPT 출력에서 ​​디코딩된다. Inference 과정에서는 학습된 모델을 reverse diffusion process에 적용하여 랜덤하게 초기화된 Gaussian 샘플을 반복적으로 denoise한다.

3. Practical Training Considerations

무한한 장면 형상을 위한 homogeneous coordinates

실제 장면은 여러 장면 간, 그리고 단일 장면 내에서 상당한 scale 변화를 보이는 경우가 많다. 3D 포인트의 평균 거리로 정규화하면 장면 간 변동을 해결하는 데 도움이 되지만, 장면 내 변동은 여전히 ​​존재한다. 예를 들어, 배경 건물이 전경 요소보다 훨씬 멀리 떨어져 있을 수 있으며, 이는 실제 광선 원점과 끝점을 생성할 때 매우 큰 좌표값을 초래할 수 있다. 그러나 diffusion model은 제한된 입력과 출력 범위를 사용할 때 가장 효과적으로 학습하는 경향이 있다.

저자들은 3D 장면 데이터셋에 존재하는 대규모 변동에 대한 학습을 ​​안정화하기 위해, 광선 원점과 끝점을 homogeneous coordinate으로 표현하는 것을 제안하였다. 구체적으로, 임의의 3D 포인트에 대해 다음과 같이 homogeneous transform을 적용한다.

\[\begin{equation} (x, y, z) \rightarrow \frac{1}{w} (x, y, z, 1) \end{equation}\]

여기서 $w$는 임의의 scale factor이며, 유계 좌표를 사용하기 위해 homogeneous coordinate이 unit-norm이 되도록 $w$를 선택한다.

\[\begin{equation} w := \sqrt{x^2 + y^2 + z^2 + 1} \end{equation}\]

단위 정규화를 통해 동차 좌표를 무한한 장면 형상에 대한 유계 표현으로 사용할 수 있다. 예를 들어, $(x, y, z, 0)$은 $(x, y, z)$ 방향으로 무한대에 있는 점이다. 이 표현을 사용하면 학습 중에 큰 좌표 값을 더 쉽게 다룰 수 있다.

불완전한 GT를 이용한 학습

많은 현실 데이터셋은 sparse한 포인트 클라우드만 제공하여 불완전한 깊이 정보를 생성한다. 이는 diffusion model 학습에 심각한 문제를 야기하는데, 광선 끝점을 생성하는 데 사용되는 GT 깊이 값에 유효하지 않거나 누락된 데이터가 포함되는 경우가 많기 때문이다. 이러한 누락된 광선 끝점을 타겟 분포의 일부로 해석하는 것은 매우 바람직하지 않으며, diffusion model은 학습 중에 불완전한 입력을 처리해야 한다.

이 문제를 완화하기 위해, DiT 입력에 GT 마스크 $\mathcal{M} \in \mathbb{R}^{N \times H \times W}$를 추가로 적용하며, 0 값은 유효하지 않은 깊이를 가진 픽셀을 나타낸다. 학습 과정에서 noise가 추가된 광선과 GT 마스크를 element-wise로 곱한 다음 채널 차원을 따라 concat한다.

\[\begin{equation} \mathcal{S}_t^\prime = (\mathcal{M} \cdot \mathcal{S}_t) \oplus \mathcal{M} \end{equation}\]

그런 다음, 마스킹되지 않은 픽셀에 대해서만 diffusion loss를 계산한다. 이를 통해, 학습 과정에서 모델이 유효한 GT 값을 가진 영역에 집중하도록 한다. Inference 시에는 diffusion process가 모든 픽셀에서 광선의 원점과 끝점을 추정하도록 해야 하므로, 항상 값이 1로 설정된 GT 마스크를 사용한다.

Sparse-to-Dense Training

전체 모델을 처음부터 학습하는 것은 수렴 속도가 느리고 최적이 아닌 성능을 초래하기 때문에, sparse-to-dense training 방식을 사용하였다. 먼저, DPT 디코더를 제거하고 출력 광선 원점과 끝점이 DINOv2 feature와 동일한 공간 해상도를 갖는 sparse 버전의 모델을 학습시킨다. 공간적 다운샘플링이 필요하지 않으므로, 이 sparse 모델은 하나의 linear layer를 사용하여 noise가 추가된 광선 원점과 끝점을 임베딩한다. Sparse 모델이 학습되면 학습된 가중치를 사용하여 dense 모델 DiT를 초기화한다.

Experiments

• 데이터셋: Habitat, CO3D, ScanNet++, ArkitScenes, Static Scenes 3D, MegaDepth, BlendedMVS

1. Evaluation on CO3D

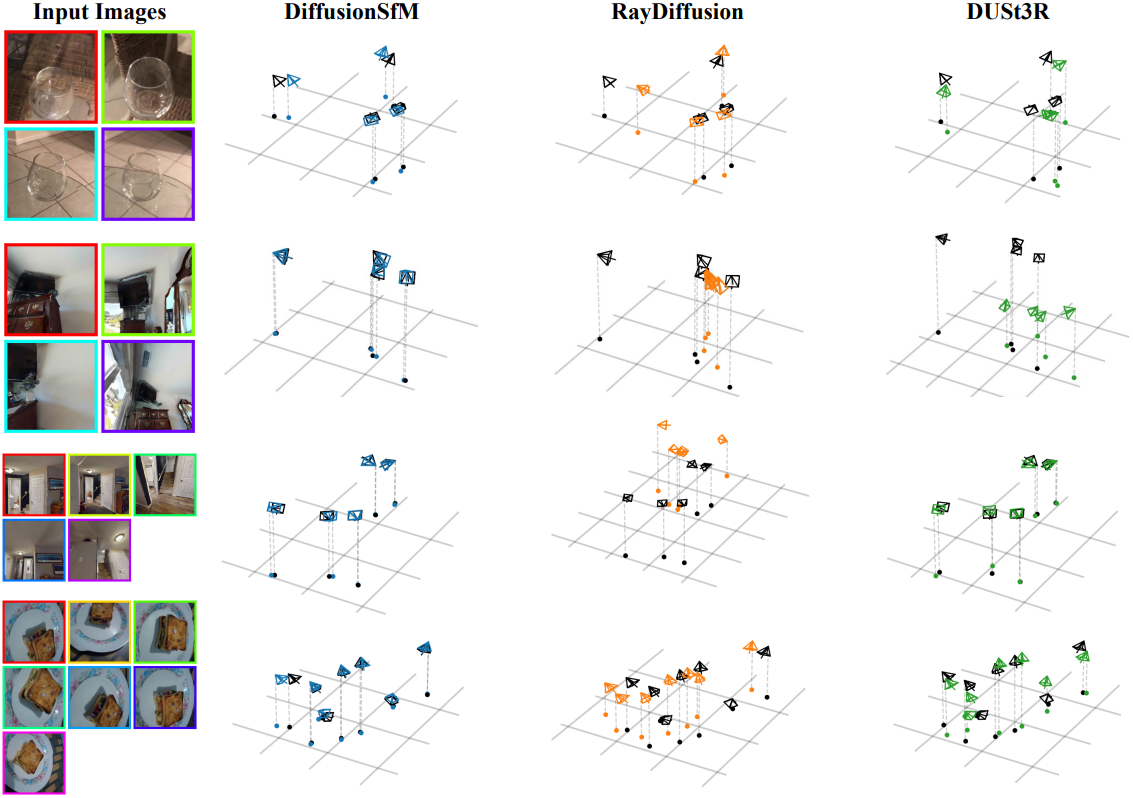
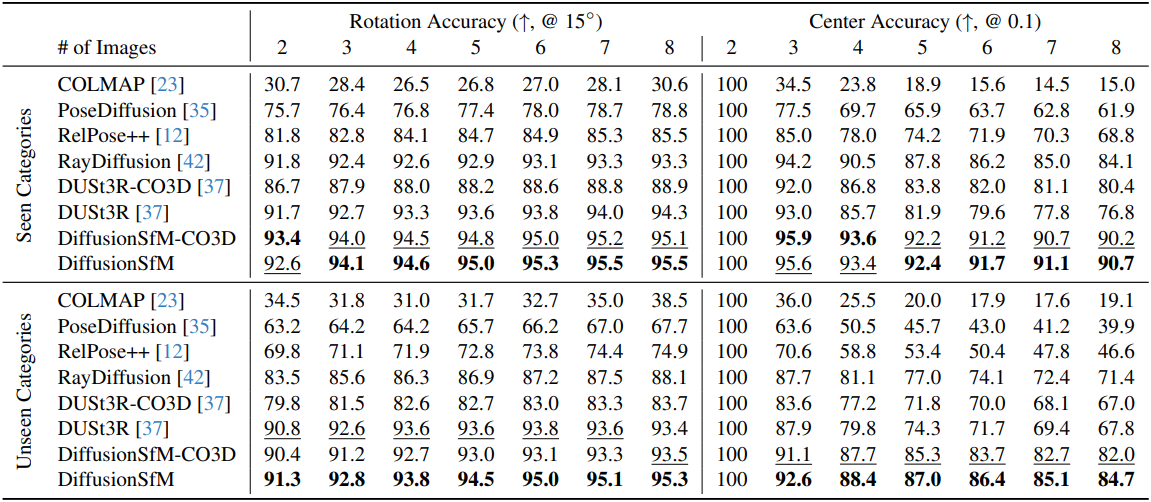
다음은 CO3D에서 카메라 포즈 정확도를 비교한 결과이다.

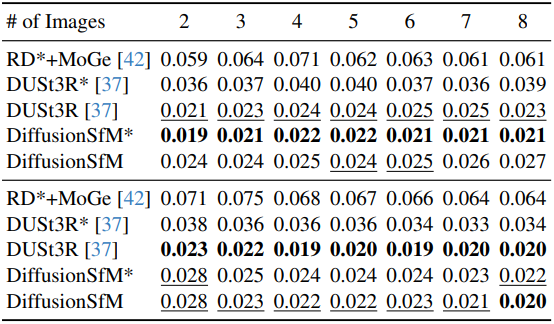
다음은 CO3D에서 형상 정확도를 비교한 결과이다. (Chamfer Distance)

2. Evaluation on Scene-Level Datasets

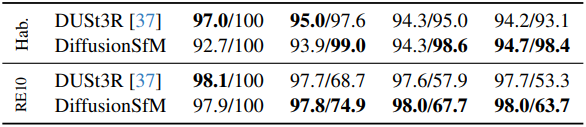
다음은 Habitat과 RealEstate10k에서의 카메라 포즈 정확도를 비교한 결과이다. (rotation / center)

3. Ablation Study

다음은 GT 마스크 컨디셔닝에 대한 ablation 결과이다. (CO3D)

4. Multi-modality from Multiple Sampling

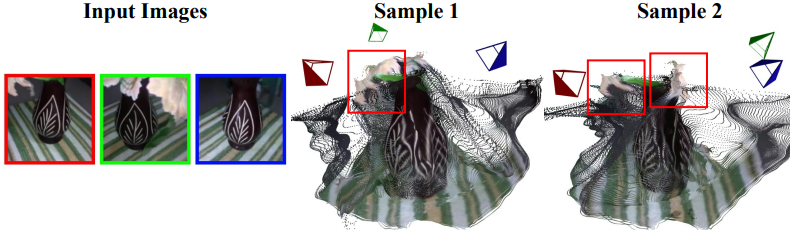
다음은 동일한 입력 이미지에 대하여 다른 랜덤 noise으로 샘플링한 결과를 비교한 것이다.