[논문리뷰] Diffusion-LM Improves Controllable Text Generation

NeurIPS 2022. [Paper] [Github]
Xiang Lisa Li, John Thickstun, Ishaan Gulrajani, Percy Liang, Tatsunori B. Hashimoto
Stanford University
27 May 2022

Introduction

대규모 autoregressive 언어 모델(LM)은 고품질 텍스트를 생성할 수 있지만 이러한 LM을 실제 애플리케이션에 안정적으로 적용하려면 텍스트 생성 프로세스를 제어할 수 있어야 하며, 원하는 요구 사항(ex. 주제, 구문 구조)을 충족하는 텍스트를 생성해야 한다. LM을 제어하기 위한 자연스러운 접근 방식은 (제어, 텍스트) 형식의 supervised 데이터를 사용하여 LM을 finetuning하는 것이다. 그러나 각 제어 task에 대한 LM 파라미터를 업데이트하는 것은 비용이 많이 들 수 있으며 여러 제어 구성을 허용하지 않는다. 이는 생성된 텍스트가 제어를 얼마나 잘 만족시키는지 측정하는 외부 classifier를 사용하여 LM을 고정하고 생성 프로세스를 조정하는 light-weight 및 modular plug-and-play 접근 방식에 동기를 부여한다. 그러나 고정된 autoregressive LM을 조정하는 것은 어려운 것으로 나타났으며 기존의 성공은 단순한 속성 수준 제어(ex. 감정이나 주제)로 제한되었다.

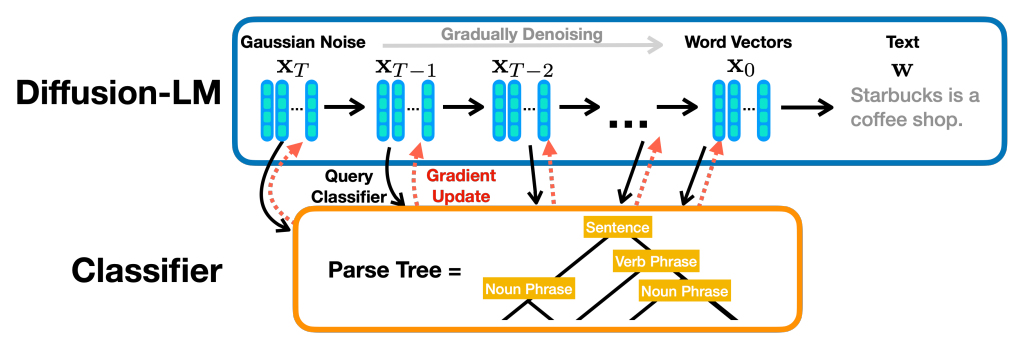
본 논문은 보다 복잡한 제어를 다루기 위해 연속적인 diffusion에 기반한 새로운 언어 모델인 Diffusion-LM을 제안한다. Diffusion-LM은 일련의 Gaussian noise vector로 시작하여 위 그림과 같이 단어에 해당하는 벡터로 점진적으로 denoise한다. 이러한 점진적인 denoising step은 연속적인 latent 표현의 계층(hierarchy)을 생성한다. 저자들은 이 계층적이고 연속적인 latent variable이 생성된 시퀀스의 syntactic parse tree를 제한하는 것과 같은 복잡한 제어 작업을 수행하기 위한 간단한 기울기 기반 방법을 가능하게 한다는 것을 발견했다.

연속적인 diffusion model은 비전 및 오디오 도메인에서 매우 성공적이었지만 텍스트의 고유한 이산적인 특성으로 인해 텍스트에는 적용되지 않았다. Diffusion model을 텍스트에 적용하려면 표준 diffusion에 대한 몇 가지 수정이 필요하다. 표준 diffusion process에 embedding step와 rounding step을 추가하고, 임베딩을 학습하기 위한 학습 목적 함수를 설계하고, 반올림을 개선하는 기술을 제안한다.

저자들은 위 그림과 같이 기울기 기반 방법을 사용하여 Diffusion-LM을 제어한다. 이 방법을 사용하면 목표 구조 및 의미 제어를 만족하는 출력으로 텍스트 생성 프로세스를 조정할 수 있다. Diffusion-LM의 연속적인 latent variable에 대한 기울기 업데이트를 반복적으로 수행하여 유창함과 제어 만족도의 균형을 맞춘다.

Diffusion-LM의 제어를 입증하기 위해 세분화된 속성(ex. semantic content)에서 복잡한 구조(ex. syntactic parse tree)에 이르는 6개의 제어 대상을 고려한다. 본 논문의 방법은 이전 plug-and-play 방법의 성공률을 거의 두 배로 늘리고 이러한 모든 classifier-guided control task에서 finetuning 오라클과 일치하거나 능가한다. 이러한 개별 제어 task 외에도 원하는 의미 콘텐츠와 구문 구조를 모두 포함하는 문장을 생성하기 위해 여러 classifier-guided control을 성공적으로 구성할 수 있음을 보여준다. 마지막으로 길이 제어 및 채우기와 같은 스팬 고정 제어를 고려한다. Diffusion-LM을 사용하면 classifier 없이 이러한 제어 task를 수행할 수 있으며, Diffusion-LM은 이전의 plug-and-play 방법보다 성능이 훨씬 뛰어나고 채우기 task를 위해 처음부터 학습된 autoregressive LM과 동등하다.

Diffusion-LM: Continuous Diffusion Language Modeling

Diffusion-LM을 구성하려면 표준 diffusion model에 대한 몇 가지 수정이 필요하다. 먼저 이산적인 텍스트를 연속적인 space에 매핑하는 embedding function을 정의해야 한다. 이를 해결하기 위해 임베딩 학습을 위한 end-to-end 학습 목적 함수를 제안한다. 둘째, embedding space의 벡터를 다시 단어로 매핑하는 반올림 방법이 필요하다. 이를 해결하기 위해 반올림을 용이하게 하는 학습 및 디코딩 시간 방법을 제안한다.

1. End-to-end Training

이산적인 텍스트에 연속적인 diffusion model을 적용하기 위해 각 단어를 $\mathbb{R}^d$의 벡터에 매핑하는 embedding function $\textrm{EMB}(w_i)$를 정의한다. 길이가 $n$인 시퀀스 $w$의 임베딩을 다음과 같이 정의한다.

\[\begin{equation} \textrm{EMB} (w) = [\textrm{EMB}(w_1), \cdots, \textrm{EMB}(w_n)] \in \mathbb{R}^{nd} \end{equation}\]

Diffusion model의 파라미터와 단어 임베딩을 공동으로 학습하는 diffusion model 목적 함수의 수정을 제안한다. 저자들은 예비 실험에서 임의의 Gaussian 임베딩과 사전 학습된 단어 임베딩을 탐색했다. 저자들은 이러한 고정 임베딩이 end-to-end 학습과 비교하여 Diffusion-LM에 최선이 아님을 발견했다.

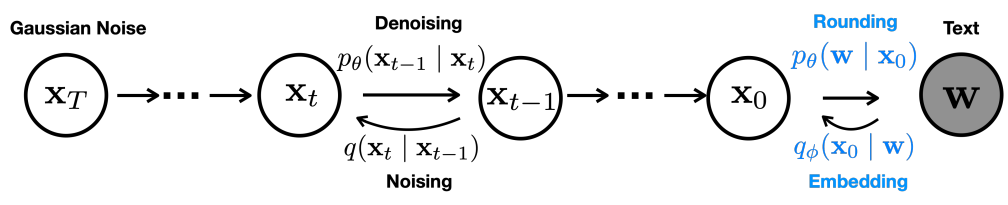
위 그림에서 볼 수 있듯이 본 논문의 접근 방식은

\[\begin{equation} q_\phi (x_\theta \vert w) = \mathcal{N}(\textrm{EMB}(w), \sigma_0 I) \end{equation}\]

로 parametrize되는 forward process에서 이산적인 단어 $w$에서 $x_0$로의 Markov transition을 추가한다. Reverse process에서

\[\begin{equation} p_\theta (w \vert x_0) = \prod_{i=1}^n p_\theta (w_i \vert x_i) \end{equation}\]

로 parametrize된 학습 가능한 반올림 step을 추가한다. 여기서 $p_\theta (w_i \vert x_i)$는 softmax 분포이다.

기존 목적 함수

\[\begin{equation} \mathcal{L}_\textrm{vlb} (x_0) = \mathbb{E}_{q(x_{1:T}, x_0)} \bigg[ \log \frac{q(x_T \vert x_0)}{p_\theta (x_T)} + \sum_{t=2}^T \log \frac{q(x_{t-1} \vert x_0, x_t)}{p_\theta (x_{t-1} \vert x_t)} - \log p_\theta (x_0 \vert x_1) \bigg] \\ \mathcal{L}_\textrm{simple} (x_0) = \sum_{t=1}^T \mathbb{E}_{q(x_t \vert x_0)} \| \mu_\theta (x_t, t) - \hat{\mu} (x_t, x_0) \|^2 \end{equation}\]

를 수정한 목적 함수는 다음과 같다.

\[\begin{equation} \mathcal{L}_\textrm{vlb}^\textrm{e2e} (w) = \mathbb{E}_{q_\phi (x_0 \vert w)} [\mathcal{L}_\textrm{vlb} (x_0) + \log q_\phi (x_0 \vert w) - \log p_\theta (w \vert x_0)] \\ \mathcal{L}_\textrm{simple}^\textrm{e2e} (w) = \mathbb{E}_{q_\phi (x_{0:T} \vert w)} [\mathcal{L}_\textrm{simple} (x_0) + \| \textrm{EMB} (w) - \mu_\theta (x_1, 1) \|^2 - \log p_\theta (w \vert x_0)] \end{equation}\]

\(\mathcal{L}_\textrm{simple}^\textrm{e2e} (w)\)는 \(\mathcal{L}_\textrm{vlb}^\textrm{e2e} (w)\)에서 유도할 수 있다. Embedding function을 학습하고 있으므로 $q_\phi$는 이제 학습 가능한 파라미터를 포함하고 reparametrization trick을 사용하여 이 샘플링 step를 통해 backpropagate한다.

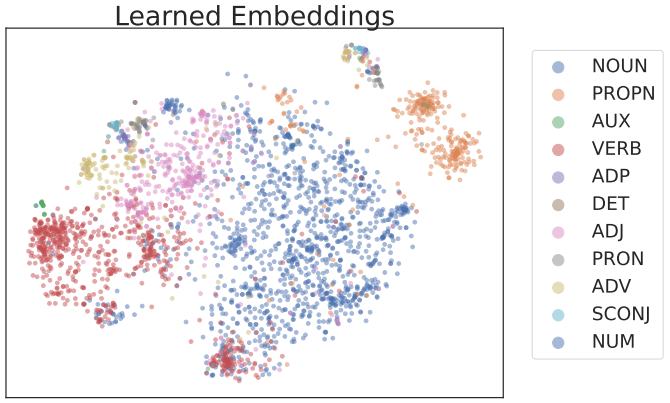
경험적으로 학습된 임베딩 클러스터가 의미 있게 발견된다. 동일한 품사 태그가 있는 단어는 위 그림과 같이 클러스터링되는 경향이 있다.

2. Reducing Rounding Errors

학습된 임베딩은 이산적인 텍스트에서 연속적인 $x_0$로의 매핑을 정의한다. Reverse process는 예측된 $x_0$를 다시 이산적인 텍스트로 반올림한다. 반올림은

\[\begin{equation} \arg \max p_\theta (w \vert x_0) = \prod_{i=1}^n p_\theta (w_i \vert x_i) \end{equation}\]

에 따라 각 위치에 대해 가장 가능성이 높은 단어를 선택하여 이루어진다. 이상적으로는 denoising step에서 $x_0$가 일부 단어의 임베딩에 정확히 놓이기 때문에 이 argmax 반올림은 이산적인 텍스트로 다시 매핑하기에 충분할 것이다. 그러나 경험적으로 모델은 단일 단어에 대응되는 $x_0$를 생성하지 못한다.

이 현상에 대한 한 가지 설명은 목적 함수의 \(\mathcal{L}_\textrm{simple} (x_0)\) 항이 $x_0$의 구조 모델링을 충분히 강조하지 않는다는 것이다. 여기서 모델 $\mu_\theta (x_t, t)$는 각 denoising step $t$에 대해 $p_\theta (x_{t-1} \vert x_t)$의 평균을 직접 예측한다. 이 목적 함수에서 $x_0$가 단일 단어 임베딩에 대응해야 하는 제약 조건은 $t$가 0에 가까운 항에만 나타날 것이며 저자들은 이 parametrization은 목적 함수가 이러한 항을 강조하도록 하기 위해 신중한 조정이 필요함을 발견했다.

본 논문의 접근 방식은 \(\mathcal{L}_\textrm{simple}\)을 다시 parametrize하여 Diffusion-LM이 목적 함수의 모든 항에서 명시적으로 $x_0$를 모델링하도록 강제한다. 구체적으로, 저자들은 x0를 통해 parametrize되는 $\mathcal{L}_\textrm{simple}$과 유사한 목적 함수

\[\begin{equation} \mathcal{L}_{x_0 - \textrm{simple}}^\textrm{e2e} (x_0) = \sum_{t=1}^T \mathbb{E}_{x_t} \| f_\theta (x_t, t) − x_0 \|^2 \end{equation}\]

를 유도하였으며, 여기서 모델 $f_\theta (x_t, t)$는 $x_0$을 직접 예측한다. 이것은 신경망이 모든 항에서 $x_0$를 예측하도록 강제하고 저자들은 이 목적 함수로 학습된 모델이 $x_0$가 단어 임베딩의 중심에 정확하게 위치해야 한다는 것을 빠르게 학습한다는 것을 발견했다.

Reparametrization이 모델 학습에 어떻게 도움이 될 수 있는지 설명했지만, 저자들은 clamping trick이라고 하는 테크닉에서 디코딩 시간에 동일한 직관이 사용될 수 있음을 발견했다. 모델은 먼저 $f_\theta (x_t, t)$를 통해 $x_0$의 추정치를 계산한 다음 이 추정치에 따라 $x_{t−1}$을 샘플링하여 $x_t$에서 $x_{t−1}$로 denoise한다.

\[\begin{equation} x_{t-1} = \sqrt{\vphantom{1} \bar{\alpha}_t} f_\theta (x_t, t) + \sqrt{1 - \bar{\alpha}_t} \epsilon, \\ \bar{\alpha}_t = \prod_{s=0}^t (1 - \beta_s), \quad \epsilon \sim \mathcal{N} (0, I) \end{equation}\]

Clamping trick에서 모델은 예측된 벡터 $f_\theta (x_t, t)$를 가장 가까운 단어 임베딩 시퀀스에 추가로 매핑한다. 이제 샘플링 step은

\[\begin{equation} x_{t-1} = \sqrt{\vphantom{1} \bar{\alpha}_t} \cdot \textrm{Clamp} (f_\theta (x_t, t)) + \sqrt{1 - \bar{\alpha}_t} \epsilon \end{equation}\]

이 된다. Clamping trick은 예측된 벡터가 중간 diffusion step을 위한 단어에 대응되도록 하여 벡터 예측을 보다 정확하게 만들고 반올림 오차를 줄인다.

Decoding and Controllable Generation with Diffusion-LM

1. Controllable Text Generation

제어에 대한 본 논문의 접근 방식은 Bayesian 공식에서 영감을 받았지만 이산적인 텍스트에서 직접 제어를 수행하는 대신 Diffusion-LM에서 정의한 연속적인 latent variable 시퀀스 $x0:T$에 대한 제어를 수행하고 반올림 step을 적용하여 이러한 latent들을 텍스트로 변환한다.

$x0:T$를 제어하는 것은 사후 확률 분포 $p (x_{0:T} \vert c) = \prod_{t=1}^T p(x_{t-1} \vert x_t, c)$에서 디코딩하는 것과 동등하며, 각 diffusion step에서 이 joint inference problem을 제어 문제의 시퀀스로 분해한다.

\[\begin{equation} p(x_{t-1} \vert x_t, c) \propto p(x_{t-1} \vert x_t) \cdot p(c \vert x_{t-1}, x_t) \end{equation}\]

추가로 조건부 독립 가정에 따라 $p(c \vert x_{t-1}, x_t) = p(c \vert x_{t-1})$로 간단하게 만들 수 있다. 결과적으로 $t$번째 step에서 $x_{t-1}$에 기울기 업데이트를 한다.

\[\begin{equation} \nabla_{x_{t-1}} \log p (x_{t-1} \vert x_t, c) = \nabla_{x_{t-1}} \log p(x_{t-1} \vert x_t) + \nabla_{x_{t-1}} \log p (c \vert x_{t-1}) \end{equation}\]

첫번째 항은 Diffusion-LM으로 parametrize되고 두번재 항은 신경망 classifier로 parametrize된다.

이미지에서의 연구와 유사하게 diffusion latent variable에 대한 classifier를 학습시키고 latent space $x_{t-1}$에서 기울기 업데이트를 하여 제어를 충족하도록 조정한다. 이미지 diffusion 연구에서는 diffusion step당 $\nabla_{x_{t-1}} \log p(c \vert x_{t−1})$ 방향으로 기울기 step을 한 번 취한다. 저자들은 텍스트의 성능을 개선하고 디코딩 속도를 높이기 위해 fluency regularization와 multiple gradient step이라는 두 가지 주요 수정 사항을 도입했다.

유창한 텍스트를 생성하기 위해 저자들은 fluency regularization을 사용하여 제어 목적 함수에 기울기 업데이트를 실행한다

\[\begin{equation} \lambda \log p(x_{t-1} \vert x_t) + \log p(c \vert x_{t−1}) \end{equation}\]

$\lambda$는 유창성 (첫번째 항)과 제어 (두 번째 항)을 절충하는 hyperparameter이다.

확산에 대한 기존의 제어 가능한 생성 방법은 목적 함수에 $\lambda \log p(x_{t-1} \vert x_t)$ 항을 포함하지 않지만 저자들은 이 항이 유창한 텍스트를 생성하는 도구임을 발견했다. 결과적으로 제어 가능한 생성 프로세스는 $p(x_{t-1} \vert x_t, c)$의 최대화와 샘플링의 균형을 맞추는 확률적 디코딩 방법으로 볼 수 있다.

제어 품질을 개선하기 위해 각 diffusion step에 대해 multiple gradient step를 수행한다. 각 diffusion step에 대해 Adagrad 업데이트를 3 step 실행한다. 계산 비용 증가를 완화하기 위해 diffusion step을 2000에서 200으로 downsampling하여 샘플 품질을 크게 손상시키지 않으면서 제어 가능한 생성 알고리즘의 속도를 높인다.

2. Minimum Bayes Risk Decoding

많은 조건부 텍스트 생성 task에는 기계 번역 또는 문장 채우기와 같은 단일 고품질 출력 시퀀스가 필요하다. 이러한 설정에서는 Minimum Bayes Risk (MBR) 디코딩을 적용하여 Diffusion-LM에서 가져온 샘플의 집합 $S$를 집계하고 loss function $\mathcal{L}$ (ex. negative BLEU score)에서 최소 기대 위험을 달성하는 샘플을 선택한다.

\[\begin{equation} \hat{w} = \underset{w \in S}{\arg \min} \sum_{w' \in S} \frac{1}{| S |} \mathcal{L} (w, w') \end{equation}\]

저자들은 낮은 품질의 샘플은 나머지 샘플과 다르고 loss function에 의해 불이익을 받기 때문에 MBR 디코딩이 고품질 출력을 반환한다는 것을 발견했다.

Experiment

• 데이터셋: E2E, ROCStories
• Hyperparameters
  • Transformer 아키텍처 기반, 시퀀스 길이 $n = 64$, diffusion step $T = 2000$, square-root noise schedule
  • 임베딩 차원: E2E는 $d = 16$, ROCStories는 $d = 128$
  • 디코딩: E2E는 diffusion step을 200으로 downsampling, ROCStories는 2000 유지
• Control tasks
  • Semantic Content: 필드 (ex. 평가)와 값 (ex. 별점 5개)이 주어지면 필드=값을 커버하는 문장을 생성. 실제 값과 일치하는 비율을 평가.
  • Parts-of-speech: 품사 (parts-of-speech) 태그의 시퀀스가 주어지면 일치하는 단어의 시퀀스를 생성. 단어 레벨에서 일치 여부 평가.
  • Syntax Tree: Syntactic parse tree가 주어지면 일치하는 문장을 생성. Parser로 생성된 텍스트를 파싱하고 F1 score를 평가.
  • Syntax Spans: (범위, syntactic 카테고리) 쌍이 주어지면 범위 $[i, j]$에 대하여 parse tree가 syntactic 카테고리 (ex. 전치사구)와 일치하는 텍스트를 생성. 일치하는 범위의 비율로 성공 여부를 정량화.
  • Length: 10에서 40 사이의 길이가 주어지면 $\pm 2$ 이내의 길이를 생성.
  • Infilling: aNLG 데이터셋에서 왼쪽 컨텍스트($O_1$)와 오른쪽 컨텍스트 ($O_2$)가 주어지면 $O_1$와 $O_2$를 논리적으로 연결하는 문장을 생성.

아래는 각 control task에 대한 입력 제어 텍스트와 출력 텍스트의 예시이다.

위 4개는 classifier를 사용하고 아래 2개는 classifier를 사용하지 않는다.

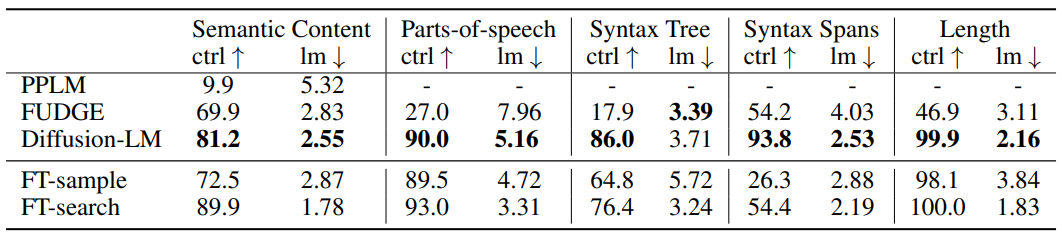
1. Classifier-Guided Controllable Text Generation Results

다음은 각 control task에 대한 성공률(ctrl)과 유창성(lm)에 대한 평가 결과이다.

다음은 Syntax Tree control의 샘플이다. 다른 모델의 실패한 범위는 빨간색으로, 이에 대응되는 Diffusion-LM의 범위는 굵게 표시되어 있다.

2. Composition of Controls

다음은 semantic control과 syntactic control을 합친 실험의 결과이다.

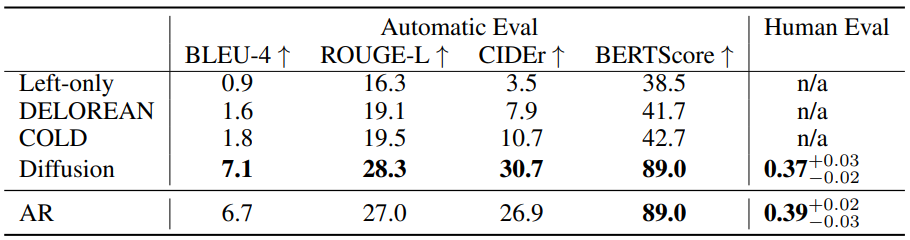
3. Infilling Results

다음은 infilling 결과이다.

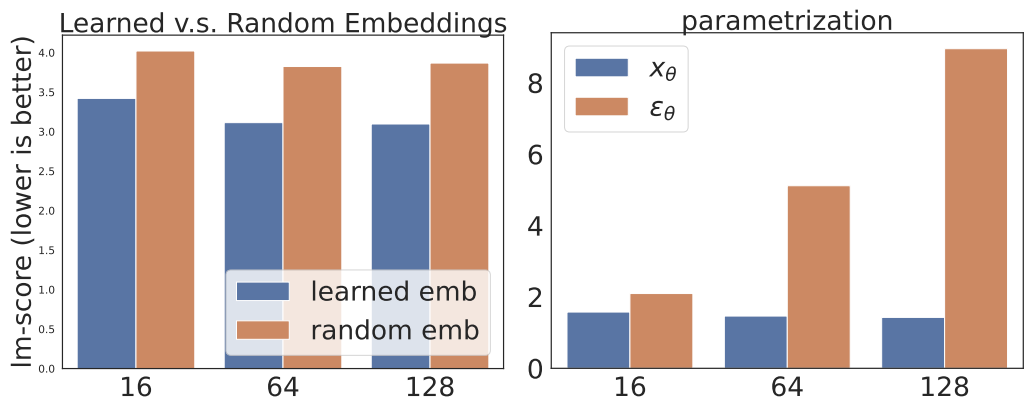
4. Ablation Studies

다음은 디자인 선택에 대한 ablation study 결과를 나타낸 그래프이다. 왼쪽은 학습된 임베딩과 랜덤 임베딩을 비교한 그래프이고, 오른쪽은 목적 함수 parametrization에 대한 그래프이다.

Limitations

Diffusion-LM에는 다음과 같은 단점이 있다.

1. Perplexity가 더 높다. (낮을수록 좋음)
2. 디코딩이 상당히 느리다.
3. 학습이 더 느리게 수렴된다.