[논문리뷰] Diffusion Forcing: Next-token Prediction Meets Full-Sequence Diffusion

NeurIPS 2024. [Paper] [Page] [Github]
Boyuan Chen, Diego Marti Monso, Yilun Du, Max Simchowitz, Russ Tedrake, Vincent Sitzmann
MIT
1 Jul 2024

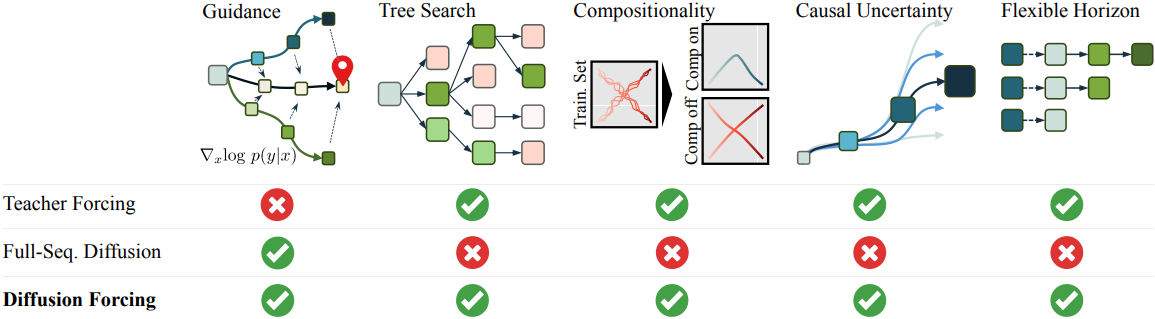
Introduction

현재의 next-token prediction model은 teacher forcing을 통해 학습되며, 모델은 이전 토큰들의 GT를 기반으로 바로 다음 토큰을 예측한다. 이로 인해 두 가지 제한이 발생한다.

1. 특정 목적 함수를 최소화하기 위해 시퀀스 샘플링을 가이드할 수 있는 메커니즘이 없다.
2. 연속적인 데이터에서 쉽게 불안정해진다.

예를 들어, 동영상을 autoregressive하게 생성하려고 할 때 프레임 간 예측의 사소한 오차가 누적되고 모델이 발산한다.

Full-sequence diffusion은 토큰을 concat한 후 diffuse하여 고정된 수의 토큰의 공동 분포를 직접 모델링한다. 여기서 noise level은 모든 토큰에서 동일한다. 원하는 시퀀스로 샘플링을 가이드하는 diffusion guidance를 사용할 수 있으며, 이는 planning에서 매우 중요하다. 또한 동영상과 같은 연속적인 신호를 생성하는 데 탁월하다.

그러나 full-sequence diffusion은 비인과적이고 마스킹되지 않은 아키텍처를 통해 parameterize되며, 이것은 guidance와 부분 시퀀스 생성의 가능성을 제한한다. 또한 full-sequence diffusion을 위한 next-token prediction model을 학습시켜 두 모델의 장점을 단순히 결합하면, 초기 토큰의 작은 불확실성이 이후 토큰의 높은 불확실성을 필요로 한다는 사실을 모델링하지 않기 때문에 직관적으로 생성이 좋지 않다.

본 논문에서는 새로운 학습 및 샘플링 패러다임인 Diffusion Forcing (DF)을 소개한다. DF는 각 토큰이 무작위적이고 독립적인 noise level과 연관되고, next-or-next-few-token prediction model을 통해 임의적이고 독립적인 토큰별 schedule에 따라 토큰을 denoise할 수 있다.

DF는 토큰에 noise를 추가하는 것이 부분 마스킹의 한 형태라는 관찰에서 동기를 얻었다. Noise가 없으면 토큰이 마스킹되지 않고, 완전히 noise면 토큰이 완전히 마스킹된다. 따라서 DF는 모델이 가변적으로 noise가 추가된 모든 토큰들을 “unmask”하는 방법을 학습하도록 강제한다. 동시에 예측을 next-token prediction model의 구성으로 parameterize함으로써 다양한 길이의 시퀀스를 유연하게 생성할 수 있을 뿐만 아니라 새로운 궤적으로 일반화할 수 있다.

저자들은 Causal Diffusion Forcing (CDF)으로 시퀀스 생성을 위한 DF를 구현하였는데, 여기서 미래 토큰은 인과적인 아키텍처를 통해 과거 토큰에 의존한다. 토큰별 독립적인 noise level로 시퀀스의 모든 토큰을 한 번에 denoise하도록 모델을 학습시킨다. 샘플링하는 동안 CDF는 Gaussian noise 프레임 시퀀스를 점진적으로 denoise하여 깨끗한 샘플로 만들며, 서로 다른 프레임이 각 denoising step에서 다른 noise level을 가질 수 있다.

Next-token prediction model과 마찬가지로 CDF는 가변 길이 시퀀스를 생성할 수 있다. Next-token prediction과 달리 바로 다음 토큰에서 미래의 수천 개의 토큰까지 안정적으로 이를 수행한다. 연속적인 토큰의 경우에도 마찬가지이다. 게다가 full-sequence diffusion과 마찬가지로 높은 reward 생성에 대한 guidance를 허용한다. CDF는 인과성, 유연한 horizon, 가변 noise schedule을 활용함으로써 새로운 능력인 Monte Carlo Guidance (MCG)를 가능하게 하고, 인과적이지 않은 full-sequence diffusion model에 비해 reward가 높은 생성의 샘플링을 획기적으로 개선한다.

Method

1. Noising as partial masking

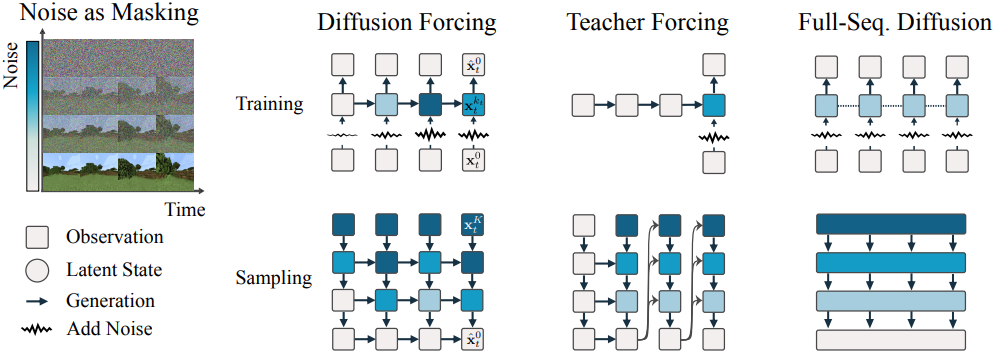
일반성을 잃지 않고 순차적이든 아니든 모든 토큰 모음을 $t$로 인덱싱된 순서 있는 집합으로 볼 수 있다. Teacher forcing으로 next-token prediction을 학습시키는 것은 시간 $t$에서 각 토큰 \(\textbf{x}_t\)를 마스킹하고 과거 \(\textbf{x}_{1:t−1}\)로부터 예측하는 것으로 해석할 수 있다. 이러한 모든 기법을 시간 축을 따라 마스킹하는 것으로 간주한다.

또한 full-sequence forward diffusion, 즉 데이터 \(\textbf{x}_{1:T}^0 = \textbf{x}_{1:T}\)에 점진적으로 noise를 추가하는 과정을 부분 마스킹의 한 형태로 볼 수 있으며, 이를 노이즈 축을 따라 마스킹하는 것이라고 부른다. 실제로, $K$ step의 noise 추가 후 \(\textbf{x}_{1:T}^K\)는 대략적으로 원본 데이터에 대한 정보가 없는 순수한 noise가 된다.

본 논문은 마스킹의 두 축을 통합하였다. 토큰 시퀀스는 \(\textbf{x}_{1:T}\)로 표시하며, 아래 첨자는 시간 축을 나타낸다. \(\textbf{x}_t^{k_t}\)는 forward diffusion process에서 noise level $k_t$에서의 \(\textbf{x}_t\)를 나타낸다. \(\textbf{x}_t^0 = \textbf{x}\)는 noise가 없는 토큰이고, \(\textbf{x}_t^K = \mathcal{N}(0, \textbf{I})\)이다. 따라서 \((\textbf{x}_t^{k_t})_{1 \le t \le T}\)는 각 토큰이 서로 다른 noise level $k_t$를 갖는 입력 시퀀스를 나타내며, noising을 통해 각 토큰에 적용된 부분 마스킹의 정도로 볼 수 있다.

2. Diffusion Forcing: different noise levels for different tokens

Diffusion Forcing (DF)은 임의의 시퀀스 길이의 noise가 추가된 토큰 \((\textbf{x}_t^{k_t})_{1 \le t \le T}\)를 학습시키고 샘플링하기 위한 프레임워크로, 여기서 중요한 점은 각 토큰의 noise level $k_t$가 timestep에 따라 달라질 수 있다는 것이다. 본 논문에서는 시계열 데이터에 초점을 맞추고, 따라서 인과적인 아키텍처, 즉 \(\textbf{x}_t^{k_t}\)는 과거 토큰에만 의존하도록 하였다. 이를 Causal Diffusion Forcing (CDF)이라고 한다. 단순함을 위해 저자들은 RNN으로 최소한의 구현에 초점을 맞추었으며, Transformer에서도 비슷하게 CDF를 사용할 수 있다.

가중치 $\theta$를 갖는 RNN은 과거 토큰의 영향을 포착하는 latent \(\textbf{z}_t\)를 유지하고, 이는 recurrent layer를 사용하여

\[\begin{equation} \textbf{z}_t \sim p_\theta (\textbf{z}_t \vert \textbf{z}_{t-1}, \textbf{x}_t^{k_t}, k_t) \end{equation}\]

를 통해 진화하며, hidden state가 Markovian 방식으로 업데이트된다. Latent state \(\textbf{z}_t\)가 주어지면 \(p_\theta (\textbf{x}_t^0 \vert \textbf{z}_t)\)는 \(\textbf{x}_t\)를 예측한다.

Training

\(p_\theta (\textbf{z}_t \vert \textbf{z}_{t-1}, \textbf{x}_t^{k_t}, k_t)\)와 \(p_\theta (\textbf{x}_t^0 \vert \textbf{z}_t)\)는 함께 RNN unit을 형성한다. 이러한 unit은 조건 변수 \(\textbf{z}_{t-1}\)과 noise가 추가된 토큰 \(\textbf{x}_t^{k_t}\)를 입력으로 사용하여 noise가 없는 \(\textbf{x}_t = \textbf{x}_t^0\)을 예측한다. 따라서 reparametrization을 통해 noise \(\epsilon^{k_t}\)를 예측하는 조건부 diffusion model과 동일한 입출력 동작을 하기 때문에, 기존의 diffusion loss로 Diffusion Forcing을 직접 학습시킬 수 있다.

\[\begin{equation} \mathbb{E}_{k_t, \textbf{x}_t, \epsilon_t} \sum_{t=1}^T \left[ \| \epsilon_t - \epsilon_\theta (\textbf{z}_{t-1}, \textbf{x}_t^{k_t}, k_t) \|^2 \right] \\ \textrm{where} \; k_{1:T} \sim \mathcal{U}([K]^T), \; \textbf{x}_{1:T} \sim \mathcal{D}_\textrm{train}, \; \epsilon_t \sim \mathcal{N}(0, \sigma_{k_t}^2 \textbf{I}) \end{equation}\]

Sampling

Diffusion Forcing 샘플링은 2D 그리드 \(\mathcal{K} \in [K]^{M \times T}\)에 noise schedule을 지정하여 정의할 수 있다. \(\mathcal{K}_{m,t}\)는 행 $m$에 대하여 timestep $t$에 해당하는 토큰의 noise level을 나타낸다.

길이가 $T$인 전체 시퀀스를 생성하기 위해, 먼저 토큰 \(\textbf{x}_{1:T}\)를 noise level $k = K$에 해당하는 순수한 noise로 초기화한다. 행별로 열을 따라 왼쪽에서 오른쪽으로 noise를 제거하여 $\mathcal{K}$로 규정된 noise level을 만든다. 마지막 행 $m = 0$에서 토큰은 noise가 모두 제거된 깨끗한 버전이다 (\(\mathcal{K}_{0,t} = 0\)).

Hyperparameter \((\alpha_k, \bar{\alpha}_k), \sigma_k\)는 DDPM과 동일하다. Diffusion Forcing은 모든 noise level 시퀀스의 토큰에 대한 noise를 제거하도록 학습되므로, 모델을 다시 학습시키지 않고도 다양한 동작을 유연하게 달성하도록 행렬 $\mathcal{K}$를 설계할 수 있다.

3. New Capabilities in Sequence Generation

Autoregressive한 생성의 안정화

동영상와 같은 고차원 연속 시퀀스의 경우, 특히 학습에 사용된 horizon을 넘어 샘플링할 때 autoregressive 아키텍처가 발산하는 것으로 알려져 있다. 반면, Diffusion Forcing은 작은 noise level $0 < k \ll K$의 약간의 noise가 추가된 토큰과 관련된 이전 latent를 사용하여 latent들을 업데이트함으로써 학습 시퀀스 길이를 넘어 긴 시퀀스를 안정적으로 rollout할 수 있다.

미래의 불확실성을 유지 (zig-zag schedule)

일련의 순수한 noise 토큰 \([\textbf{x}_1^K, \textbf{x}_2^K, \textbf{x}_3^K]^\top\)에서 시작하여 첫 번째 토큰을 완전히, 두 번째 토큰을 부분적으로 denoising하여 \([\textbf{x}_1^0, \textbf{x}_2^{K/2}, \textbf{x}_3^K]^\top\)를 생성한 다음, \([\textbf{x}_1^0, \textbf{x}_2^0, \textbf{x}_3^{K/2}]^\top\)를 생성하고 마지막으로 모든 토큰을 완전히 denoising하여 \([\textbf{x}_1^0, \textbf{x}_2^0, \textbf{x}_3^0]^\top\)을 생성할 수 있다.

Noise level을 불확실성으로 해석하면 이 샘플링 방식은 직관적으로 당장의 미래를 먼 미래보다 더 확실하게 인코딩한다.

Long-horizon Guidance

부분적으로 diffuse된 궤적 \(\textbf{x}_{1:T}\)에 guidance를 추가할 수 있다. 미래 토큰이 과거 토큰에 의존하기 때문에, 미래 토큰에서 발생한 guidance gradient는 시간 역방향으로 전파될 수 있다.

Diffusion Forcing의 고유한 장점은, 과거 토큰을 완전히 diffuse시키지 않고 미래 토큰만 diffuse시킬 수 있기 때문에, gradient가 과거 토큰의 샘플링을 가이드할 수 있다는 점이다. 이를 통해 인과성을 유지하면서도 긴 시퀀스에 대한 guidance를 효과적으로 제공할 수 있다.

4. Diffusion Forcing for Flexible Sequential Decision Making

Diffusion Forcing은 순차적 의사 결정 (sequential decision making, SDM)을 위한 새로운 프레임워크에 동기를 부여하며, 로봇 및 자율 에이전트에 응용할 수 있다.

Dynamics가 \(p(\textbf{s}_{t+1} \vert \textbf{s}_t, \textbf{a}_t)\), observation이 \(p(\textbf{o}_t \vert \textbf{s}_t)\), reward가 \(p(\textbf{r}_t \vert \textbf{s}_t, \textbf{a}_t)\)인 environment로 정의된 Markov Decision Process (MDP)를 고려하자. 목표는 궤적의 예상 누적 reward \(\mathbb{E}[\sum_{t=1}^T \textbf{r}_t]\)가 최대화되도록 policy \(\pi (\textbf{a}_t \vert \textbf{o}_{1:t})\)를 학습하는 것이다.

토큰은 \(\textbf{x}_t = [\textbf{a}_t, \textbf{r}_t, \textbf{o}_{t+1}]^\top\)으로 할당한다. 궤적은 가변 길이의 시퀀스 \(\textbf{x}_{1:T}\)이다. 앞서 설명한 방법대로 학습이 수행되며, 각 step $t$에서 noise가 없는 과거 토큰 \(\textbf{x}_{1:t-1}\)은 latent \(\textbf{z}_{t-1}\)로 요약된다. 이 latent를 조건으로 예측된 action, reward, observation을 포함하는 \(\hat{\textbf{x}}_t = [\hat{\textbf{a}}_t, \hat{\textbf{r}}_t, \hat{\textbf{o}}_{t+1}]^\top\)인 계획 \(\hat{\textbf{x}}_{t:t+H}\)를 샘플링한다. 계획된 action \(\hat{\textbf{a}}_t\)를 취하면, environment는 reward \(\textbf{r}_t\)와 다음 observation \(\textbf{o}_{t+1}\)을 생성하여 다음 토큰 \(\textbf{x}_t = [\hat{\textbf{a}}_t, \textbf{r}_t, \textbf{o}_{t+1}]^\top\)을 생성한다. Latent 토큰은 \(p_\theta (\textbf{z}_t \vert \textbf{z}_{t-1}, \textbf{x}_t, 0)\)에 따라 업데이트된다.

유연한 horizon

Diffusion Forcing은 각 새로운 action이 순차적으로 선택되기 때문에 가변적인 horizon의 task에 사용될 수 있으며, lookahead window $H$는 더 낮은 대기 시간으로 단축되거나, 아키텍처를 재학습시키거나 수정하지 않고도 긴 horizon의 계획을 수행하도록 연장될 수 있다.

Diffuser와 같은 full-sequence diffusion model은 가변적인 horizon의 task에 사용할 수 없으며, diffusion policy는 고정된 작은 $H$가 필요하다.

유연한 reward guidance

Diffusion Forcing은 미래 step들에 대해 특정한 reward를 사용하여 guidance를 통해 계획할 수 있다. 예를 들어, 다음과 같은 reward를 모두 사용할 수 있다.

• 전체 궤적에 대한 dense reward: \(\sum_{t=1}^T \textbf{r}_t\)
• 미래 lookahead에 대한 dense reward: \(\sum_{t^\prime = t}^{t+H} \textbf{r}_t\)
• 목표 완료를 나타내는 sparse reward: \(- \| \textbf{o}_T - \textbf{g} \|^2\)

Monte Carlo Guidance (MCG), future uncertainty

CDF는 미래 \(\textbf{x}_{t+1:T}\)의 전체 분포에 대한 guidance를 통해 토큰 \(\textbf{x}_t^k\)의 생성에 영향을 미칠 수 있게 해준다. 이 guidance gradient를 계산하기 위해 하나의 궤적을 샘플링하는 대신, 미래의 여러 궤적을 샘플링하여 guidance gradient의 평균을 취할 수 있다. 이를 Monte Carlo Guidance (MCG)라고 부른다.

\(\textbf{x}_t^k\)는 특정 결과 하나가 아닌 모든 미래 결과의 분포에 대한 예상 reward에 따라 가이드된다. 바로 다음 토큰의 noise를 제거할 때 미래 토큰의 noise level을 높게 유지하는 샘플링 schedule과 결합하면 MCG의 효과가 더욱 향상되며 (ex. zig-zag schedule), 미래에 대한 불확실성이 더 커진다.

Experiments

1. Video Prediction: Consistent, Stable Sequence Generation and Infinite Rollout

다음은 동영상 생성 결과를 비교한 것이다.

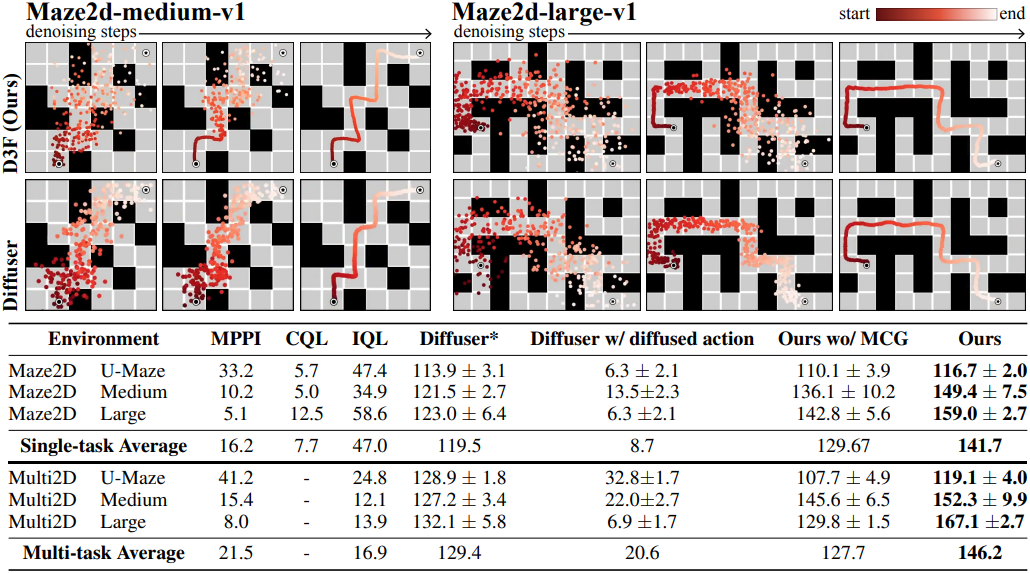
2. Diffusion Planning: MCG, Causal Uncertainty, Flexible Horizon Control

다음은 Diffusion Forcing을 planning에 사용한 결과이다.

3. Robotics: Long horizon imitation learning and robust visuomotor control

다음은 Diffusion Forcing을 실제 로봇 task에 사용한 결과이다. 로봇 팔은 세 번째 슬롯을 사용하여 두 과일의 슬롯을 바꾸도록 요청받는다.