[논문리뷰] Diffusion Model Alignment Using Direct Preference Optimization

arXiv 2023. [Paper] [Github]
Bram Wallace, Meihua Dang, Rafael Rafailov, Linqi Zhou, Aaron Lou, Senthil Purushwalkam, Stefano Ermon, Caiming Xiong, Shafiq Joty, Nikhil Naik
Salesforce AI | Stanford University
21 Nov 2023

Introduction

Text-to-image (T2I) diffusion model은 일반적으로 방대한 텍스트-이미지 쌍의 데이터셋에 diffusion 목적 함수를 적용하여 하나의 단계로 학습된다. 이는 두 단계로 학습을 받는 LLM과 대조된다. 첫 번째 사전 학습 단계에서는 대규모 데이터에 대해 학습된다. 두 번째 정렬(alignment) 단계에서는 인간의 선호도에 더 잘 맞도록 fine-tuning된다. 정렬은 일반적으로 선호도 데이터를 사용하는 supervised fine-tuning (SFT)이나 Reinforcement Learning from Human Feedback (RLHF)을 사용하여 수행된다.

LLM 정렬 프로세스의 성공에도 불구하고 대부분의 T2I diffusion model의 학습 파이프라인은 인간 선호도에 따른 학습을 통합하지 않는다. 여러 diffusion model들은 대규모 사전 학습 후 고품질 텍스트-이미지 쌍 데이터셋을 fine-tuning하여 생성 프로세스를 전략적으로 편향시킨다. 이 접근 방식은 LLM의 정렬 방법보다 강력하고 유연하지 않다.

최근에는 diffusion model을 인간의 선호도에 맞게 조정하는 방법들이 개발했지만, 일련의 피드백에 걸쳐 완전히 개방된 어휘로 안정적으로 일반화할 수 있는 능력은 입증되지 않았다. 강화학습 기반 방법은 제한된 프롬프트 세트에 매우 효과적이지만 어휘가 확장되면 효율성이 감소한다. 다른 방법들은 mode collapse 문제가 발생하거나 상대적으로 좁은 피드백 유형에서만 학습시킬 수 있다.

본 논문은 인간 선호도 데이터에 대한 diffusion model을 직접 최적화하는 방법을 개발하여 diffusion model 정렬의 이러한 격차를 처음으로 해결했다. 저자들은 쌍을 이루는 인간 선호도 데이터에 대해 생성 모델이 학습되어 reward model을 암시적으로 추정하는 DPO를 일반화하였다. 새로운 공식의 diffusion model 하에서 data likelihood의 개념을 정의하고 간단하지만 효과적인 loss를 도출하였다. 이 방법을 Diffusion-DPO라고 부르며, 안정적이고 효율적인 선호도 학습이 가능하다.

본 논문은 SDXL-1.0과 같은 SOTA T2I diffusion model을 fine-tuning하여 Diffusion-DPO의 효과를 입증하였다. DPO로 조정된 SDXL의 이미지와 일반 SDXL의 이미지를 비교하였을 때 69%의 평가자들이 DPO로 조정된 SDXL을 선택하였다. 또한 Diffusion-DPO 목적 함수를 사용하여 인간 선호도 대신 AI 피드백을 통해 학습하는 것도 효과적이다.

Background

Reward 모델링

컨디셔닝 $c$가 주어지면 생성된 이미지 $x_0$에 대한 인간의 편향성을 추정하는 것은 reward model $r(c, x_0)$에 접근할 수 없기 때문에 어렵다. 따라서 동일한 $c$에서 생성된 이미지 사이의 순위 쌍에만 접근한다고 가정한다.

\[\begin{equation} x_0^w \succ x_0^l \; \vert \; c \end{equation}\]

여기서 $x_0^w$와 $x_0^l$은 “승리” 샘플과 “패배” 샘플이다. Bradley-Terry 모델은 인간의 선호도를 다음과 같이 규정한다.

\[\begin{equation} p_\textrm{BT} (x_0^w \succ x_0^l \; \vert \; c) = \sigma (r (c, x_0^w) - r (c, x_0^l)) \end{equation}\]

$\sigma$는 시그모이드 함수이다. $r(c, x_0)$은 신경망 $\phi$에 의해 parameterize될 수 있으며 binary classification에 대한 maximum likelihood 학습을 통해 추정될 수 있다.

\[\begin{equation} L_\textrm{BT} = - \mathbb{E}_{c, x_0^w, x_0^l} [\log \sigma (r_\phi (c, x_0^w) - r_\phi (c, x_0^l))] \end{equation}\]

RLHF

RLHF는 정의된 reward model $r(c, x_0)$가 최대화되도록 조건부 분포 $p_\theta (x_0 \vert c)$를 최적화하는 동시에 레퍼런스 분포 $p_\textrm{ref}$로부터 KL-divergence를 정규화하는 것을 목표로 한다.

\[\begin{equation} \max_{p_\theta} \mathbb{E}_{c \sim \mathcal{D}_c, x_0 \sim p_\theta (x_0 \vert c)} [r(c, x_0) - \beta \mathbb{D}_\textrm{KL} [p_\theta (x_0 \vert c) \| p_\textrm{ref} (x_0 \vert c)]] \end{equation}\]

$\beta$는 정규화를 제어하는 hyperparameter이다.

DPO 목적 함수

RLHF 식에서 고유한 최적해 $p_\theta^\ast$는 다음 형식을 취한다.

\[\begin{equation} p_\theta^\ast (x_0 \vert c) = \frac{p_\textrm{ref} (x_0 \vert c) \exp (r(c, x_0) / \beta)}{Z (c)} \\ \textrm{where} \quad Z(c) = \sum_{x_0} p_\textrm{ref} (x_0 \vert c) \exp (r(c, x_0) / \beta) \end{equation}\]

따라서 reward function은 다음과 같다.

\[\begin{equation} r(c, x_0) = \beta \log \frac{p_\theta^\ast (x_0 \vert c)}{p_\textrm{ref} (x_0 \vert c)} + \beta \log Z(c) \end{equation}\]

\(L_\textrm{BT}\) 식을 사용하면 reward 목적 함수는 다음과 같다.

\[\begin{equation} L_\textrm{DPO} (\theta) = -\mathbb{E}_{c, x_0^w, x_0^l} \bigg[ \log \sigma \bigg( \beta \log \frac{p_\theta (x_0^w \vert c)}{p_\textrm{ref} (x_0^w \vert c)} - \beta \log \frac{p_\theta (x_0^l \vert c)}{p_\textrm{ref} (x_0^l \vert c)} \bigg) \bigg] \end{equation}\]

DPO for Diffusion Models

DPO를 diffusion model에 적용할 때 데이터셋 \(D = \{(c, x_0^w, x_0^l )\}\)이 있다고 생각하자. $c$는 프롬프트이고, $x_0^w$와 $x_0^l$은 레퍼런스 모델 $p_\textrm{ref}$가 $c$에 대해 생성한 이미지 쌍이며 $x_0^w$가 $x_0^l$보다 더 선호되는 이미지이다. 본 논문의 목표는 인간 선호도에 맞춰 더 선호하는 이미지를 생성하는 새로운 모델 $p_\theta$를 학습시키는 것이다.

한 가지 주요 과제는 $x_0$로 이어지는 가능한 모든 diffusion 경로 $(x_1, \ldots, x_T)$를 marginalize out 해야 하기 때문에 $p_\theta (x_0 \vert c)$가 다루기 어렵다는 것이다. 이러한 문제를 극복하기 위해 evidence lower bound (ELBO)을 활용한다. 여기서는 latent $x_{1:T}$를 도입하고 $R(c, x_{0:T})$를 전체 체인에 대한 reward로 정의하여 $r(c, x_0)$을 다음과 같이 정의할 수 있다.

\[\begin{equation} r(c, x_0) = \mathbb{E}_{p_\theta (x_{1:T} \vert x_0, c)} [R (c, x_{0:T})] \end{equation}\]

RLHF 식에 이를 적용하면 다음과 같다.

\[\begin{equation} \max_{p_\theta} \mathbb{E}_{c \sim \mathcal{D}_c, x_{0:T} \sim p_\theta (x_{0:T} \vert c)} [r(c, x_0) - \beta \mathbb{D}_\textrm{KL} [p_\theta (x_{0:T} \vert c) \| p_\textrm{ref} (x_{0:T} \vert c)]] \end{equation}\]

이 목적 함수는 reverse process의 분포를 일치시키면서 $p_\theta$에 대한 reward를 최대화하는 것을 목표로 한다. 마찬가지로 DPO 목적 함수에 궤적 $x_{0:T}$를 적용하면 다음과 같다.

\[\begin{equation} L_\textrm{DPO-Diffusion} (\theta) = -\mathbb{E}_{(x_0^w, x_0^l) \sim \mathcal{D}} \log \sigma \bigg( \beta \mathbb{E}_{\substack{x_{1:T}^w \sim p_\theta (x_{1:T}^w \vert x_0^w) \\ x_{1:T}^l \sim p_\theta (x_{1:T}^l \vert x_0^l)}} \bigg[ \log \frac{p_\theta (x_{0:T}^w)}{p_\textrm{ref} (x_{0:T}^w)} - \log \frac{p_\theta (x_{0:T}^l)}{p_\textrm{ref} (x_{0:T}^l)} \bigg] \bigg) \end{equation}\]

간결함을 위해 $c$를 생략했다. 위 식을 최적화하려면 $x_{1:T}$을 샘플링해야 한다. 이 샘플링 절차는 $T$가 일반적으로 크므로 비효율적이며, $p_\theta (x_{1:T})$를 다루기 어렵다.

\[\begin{equation} p_\theta (x_{1:T}) = p_\theta (x_T) \prod_{t=1}^T p_\theta (x_{t-1} \vert x_t) \end{equation}\]

\(L_\textrm{DPO-Diffusion} (\theta)\)를 $p_\theta$와 $p_\textrm{ref}$를 역분해로 대체하고 Jensen’s inequality와 $− \log \sigma$이 볼록 함수임을 활용하여 기대값을 밖으로 밀어낸다. 이를 통해 다음과 같은 경계를 얻는다.

\[\begin{equation} L_\textrm{DPO-Diffusion} (\theta) \le - \mathbb{E}_{\substack{(x_0^w, x_0^l) \sim \mathcal{D}, t \sim \mathcal{U}(0,T) \\ x_{t-1,t}^w \sim p_\theta (x_{t-1,t}^w \vert x_0^w) \\ x_{t-1,t}^l \sim p_\theta (x_{t-1,t}^l \vert x_0^l)}} \log \sigma \bigg( \beta T \log \frac{p_\theta (x_{t-1}^w \vert x_t^w)}{p_\textrm{ref} (x_{t-1}^w \vert x_t^w)} - \beta T \log \frac{p_\theta (x_{t-1}^l \vert x_t^l)}{p_\textrm{ref} (x_{t-1}^l \vert x_t^l)} \bigg) \end{equation}\]

이제 gradient descent를 통한 효율적인 학습이 가능하다. 그러나 $p_\theta (x_{t−1}, x_t \vert x_0, c)$로부터의 샘플링은 여전히 다루기 어렵고 $r(c, x_0)$는 $p_\theta (x_{1:T} \vert x_0)$에 대한 기대값으로 계산된다. 따라서 reverse process $p_\theta (x_{1:T} \vert x_0)$를 forward process $q(x_{1:T} \vert x_0)$로 근사화한다.

\[\begin{aligned} L (\theta) = - & \mathbb{E}_{(x_0^w, x_0^l) \sim \mathcal{D}, t \sim \mathcal{U}(0,T), x_t^w \sim q (x_t^w \vert x_0^w), x_t^l \sim q (x_t^l \vert x_0^l)} \log \sigma ( - \beta T ( \\ &\qquad \mathbb{D}_\textrm{KL} (q (x_{t-1}^w \vert x_{0,t}^w) \| p_\theta (x_{t-1}^w \vert x_t^w)) - \mathbb{D}_\textrm{KL} (q (x_{t-1}^w \vert x_{0,t}^w) \| p_\textrm{ref} (x_{t-1}^w \vert x_t^w)) \\ &\qquad -\mathbb{D}_\textrm{KL} (q (x_{t-1}^l \vert x_{0,t}^l) \| p_\theta (x_{t-1}^l \vert x_t^l)) + \mathbb{D}_\textrm{KL} (q (x_{t-1}^l \vert x_{0,t}^l) \| p_\textrm{ref} (x_{t-1}^l \vert x_t^l)))) \end{aligned}\]

이 식을 단순화하면 다음과 같다.

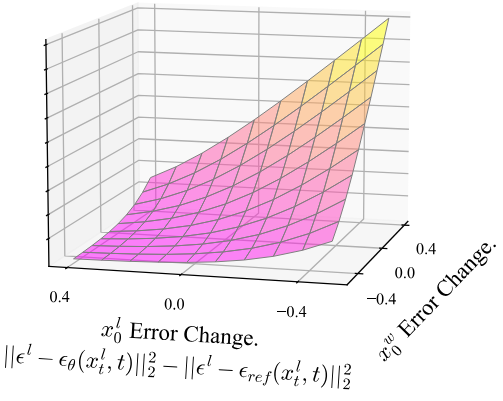
\[\begin{aligned} L (\theta) = - & \mathbb{E}_{(x_0^w, x_0^l) \sim \mathcal{D}, t \sim \mathcal{U}(0,T), x_t^w \sim q (x_t^w \vert x_0^w), x_t^l \sim q (x_t^l \vert x_0^l)} \log \sigma ( - \beta T \omega (\lambda_t) ( \\ &\qquad \| \epsilon^w - \epsilon_\theta (x_t^w, t) \|_2^2 - \| \epsilon^w - \epsilon_\textrm{ref} (x_t^w, t) \|_2^2 - (\| \epsilon^l - \epsilon_\theta (x_t^l, t) \|_2^2 - \| \epsilon^l - \epsilon_\textrm{ref} (x_t^l, t) \|_2^2) )) \end{aligned}\] \[\begin{aligned} \textrm{where} \quad & x_t^w = \alpha_t x_0^w + \sigma_t \epsilon^w, \quad \epsilon^w \sim \mathcal{N} (0, I) \\ & x_t^l = \alpha_t x_0^l + \sigma_t \epsilon^l, \quad \epsilon^l \sim \mathcal{N} (0, I) \\ & \lambda_t = \alpha_t^2 / \sigma_t^2 \end{aligned}\]

이 loss는 아래의 loss 그래프에서 볼 수 있듯이 $\epsilon_\theta$가 $x_t^l$보다 $x_t^w$의 denoising에서 더 많이 향상되도록 장려한다.

Experiments

• 데이터셋: Pick-a-Pic
• base model: SD1.5, SDXL
• 학습 디테일
  • GPU: NVIDIA A100 16개
  • batch size: 2048 (GPU당 batch size 1, gradient accumulation 128 step)
  • SD1.5: AdamW, learning rate = $2.048 \times 10^{-8}$ (25% linear warmup)
  • SDXL: Adafactor, learning rate = $8.192 \times 10^{-9}$ (25% linear warmup)

1. Primary Results: Aligning Diffusion Models

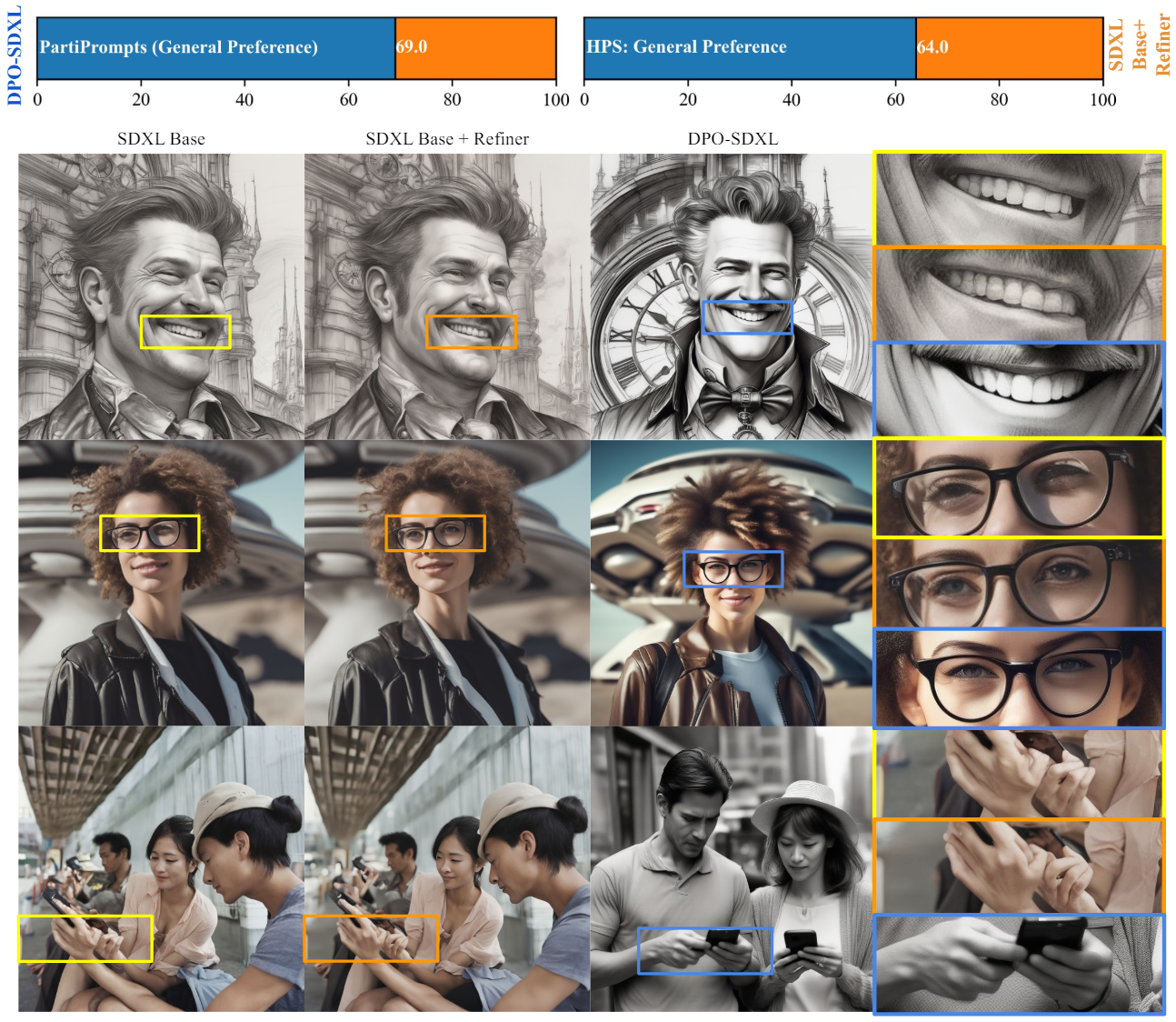
다음은 (왼쪽) PartiPrompts과 (오른쪽) HPSv2 데이터셋에 대하여 SDXL과 DPO-SDXL이 생성된 이미지들과 인간 평가자의 선호도이다.

다음은 SDXL Base + Refiner와 DPO-SDXL이 생성된 이미지들과 인간 평가자의 선호도이다.

2. Image-to-Image Editing

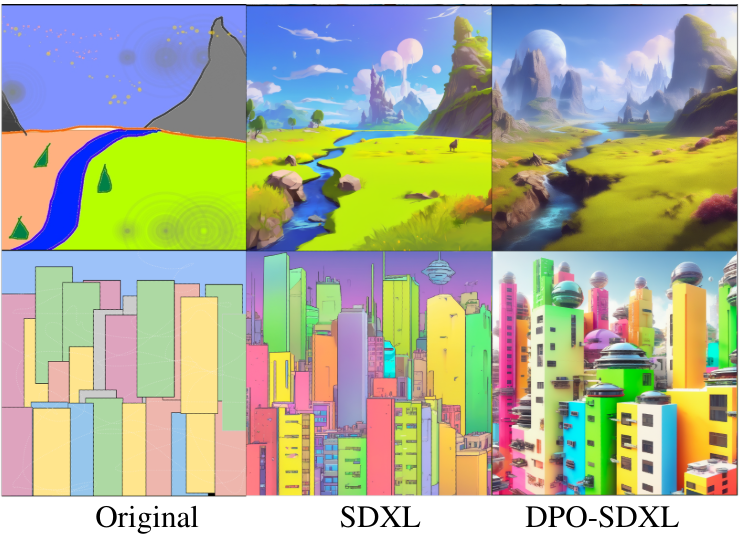
다음은 SDEdit를 사용하여 image-to-image translation task에 대한 결과를 비교한 것이다. (프롬프트: “A fantasy landscape, trending on artstation”, “High-resolution rendering of a crowded colorful sci-fi city”)

3. Learning from AI Feedback

다음은 다양한 점수 네트워크의 선호도에 따라 조정된 SD1.5를 서로 평가한 그래프이다.

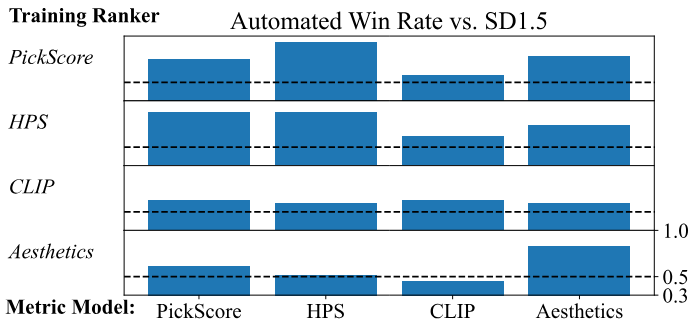
4. Analysis

다음은 Pick-a-Pic (v2) validation set에서의 선호도 정확도를 비교한 표이다.

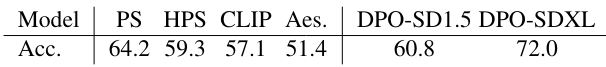
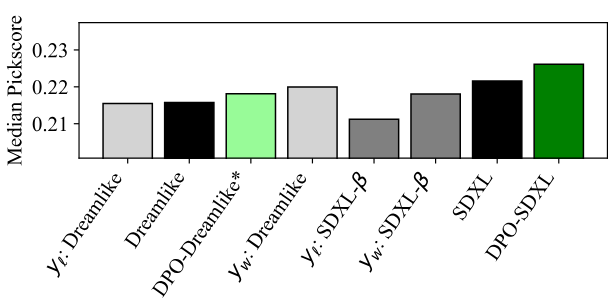
다음은 Dreamlike과 SDXL의 성능 증가를 나타낸 그래프이다. $y_l$과 $y_w$는 각각 승리 샘플과 패배 샘플의 Pickscore이다.