[논문리뷰] Your Diffusion Model is Secretly a Zero-Shot Classifier

ICCV 2023. [Paper] [Page]
Alexander C. Li, Mihir Prabhudesai, Shivam Duggal, Ellis Brown, Deepak Pathak
Carnegie Mellon University
28 Mar 2023

Introduction

Diffusion model과 같은 조건부 생성 모델은 classifier로 쉽게 변환할 수 있다. 입력 $\textbf{x}$와 선택하려는 유한한 클래스들의 집합 $\textbf{c}$가 주어지면 모델을 사용하여 class-conditional likelihood $p_\theta (\textbf{x} \, \vert \, \textbf{c})$를 계산할 수 있다. 그런 다음 적절한 prior $p(\textbf{c})$를 선택하고 베이즈 정리를 적용하면 클래스 확률 $p(\textbf{c} \, \vert \, \textbf{x})$를 얻을 수 있다.

클래스 인덱스나 프롬프트와 같이 보조 입력을 사용하는 조건부 diffusion model의 경우, ELBO를 class-conditional log likelihood \(\log p(\textbf{x} \, \vert \, \textbf{c})\)의 근사값으로 활용하여 이를 수행할 수 있다. 실제로 베이즈 정리를 통해 diffusion model classifier를 얻는 것은 noise를 반복적으로 추가하고 모든 클래스에 대한 $\epsilon$-prediction loss의 몬테카를로 추정치를 계산하는 것으로 구성된다.

이 접근 방식을 Diffusion Classifier라고 한다. Diffusion Classifier는 추가 학습 없이 text-to-image diffusion model에서 zero-shot classifier를 추출할 수 있으며, 클래스 조건부 diffusion model에서 일반적인 classifier를 추출할 수 있다. 저자들은 오차를 계산할 diffusion timestep을 적절히 선택하고 추정 확률의 분산을 줄이며 classification을 가속화하는 기술을 개발하였다.

Diffusion Classifier는 Stable Diffusion을 활용함으로써 강력한 zero-shot 정확도를 달성하고 사전 학습된 diffusion model에서 지식을 추출하기 위한 다른 접근 방식보다 성능이 뛰어나다. 또한 까다로운 Winoground compositional reasoning 벤치마크에서 가장 강력한 방법을 능가하였다. 마지막으로, 약한 augmentation만을 사용하여 ImageNet에서 79.1%의 정확도를 달성하고 동일한 데이터셋에서 학습된 discriminative classifier보다 분포 변화에 더 robust하다.

Method

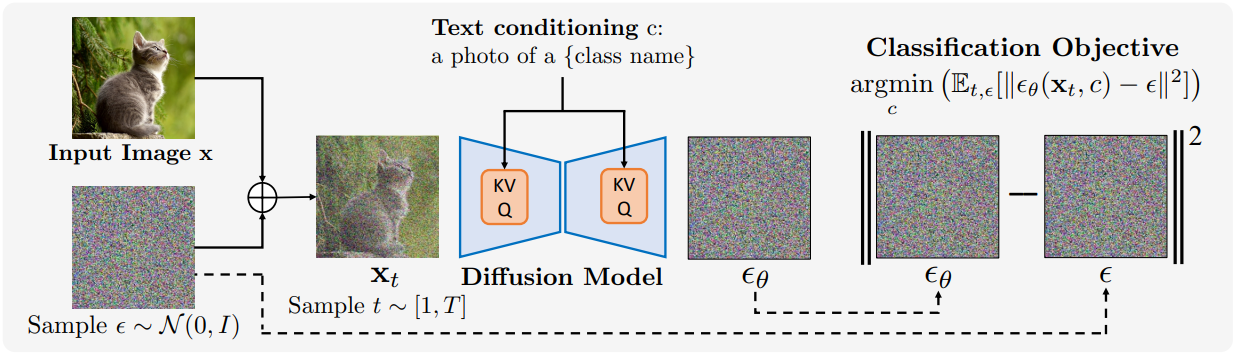
1. Classification with diffusion models

일반적으로 조건부 생성 모델을 사용한 classification은 모델 예측 \(p_\theta (\textbf{x} \, \vert \, \textbf{c}_i)\)와 레이블 \(\{\textbf{c}_i\}\)에 대한 prior $p(\textbf{c})$에 대한 베이즈 정리를 사용하여 수행할 수 있다.

\[\begin{equation} p_\theta (\textbf{c}_i \, \vert \, \textbf{x}) = \frac{p(\textbf{c}_i) \, p_\theta (\textbf{x} \, \vert \, \textbf{c}_i)}{\sum_j p(\textbf{c}_j) \, p_\theta (\textbf{x} \, \vert \, \textbf{c}_j)} \end{equation}\]

\(\{\textbf{c}_i\}\)에 대한 균일한 prior (즉, \(p(\textbf{c}_i) = \frac{1}{N}\))은 자연스럽고 모든 $p(\textbf{c})$ 항이 상쇄된다. Diffusion model의 경우 \(p_\theta (\textbf{x} \, \vert \, \textbf{c})\)를 계산하는 것은 어렵기 때문에 \(\log p_\theta (\textbf{x} \, \vert \, \textbf{c})\) 대신 ELBO

\[\begin{equation} - \mathbb{E}_{t, \epsilon} [\| \epsilon - \epsilon_\theta (\textbf{x}_t, \textbf{c}) \|^2] + C \end{equation}\]

를 사용하고, 이를 통해 \(\{\textbf{c}_i\}_{i=1}^N\)에 대한 posterior 분포를 얻을 수 있다.

\[\begin{equation} p_\theta (\textbf{c}_i \, \vert \, \textbf{x}) = \frac{\exp (- \mathbb{E}_{t, \epsilon} [\| \epsilon - \epsilon_\theta (\textbf{x}_t, \textbf{c}_i) \|^2])}{\sum_j \exp (- \mathbb{E}_{t, \epsilon} [\| \epsilon - \epsilon_\theta (\textbf{x}_t, \textbf{c}_j) \|^2])} \end{equation}\]

$N$개의 \((t_i, \epsilon_i)\) 쌍을 샘플링하여 각 기대값의 몬테카를로 추정치를 다음과 같이 계산한다. ($t_i \sim [1, 1000]$, $\epsilon \sim \mathcal{N}(0,I)$)

\[\begin{equation} \frac{1}{N} \sum_{i=1}^N \| \epsilon_i - \epsilon_\theta (\sqrt{\vphantom{1} \bar{\alpha}_{t_i}} \textbf{x} + \sqrt{1 - \bar{\alpha}_{t_i}} \epsilon_i, \textbf{c}_j) \|^2 \end{equation}\]

위 식을 \(p_\theta (\textbf{c}_i \, \vert \, \textbf{x})\)에 대입하면 모든 조건부 diffusion model에서 classifier를 추출할 수 있다. 이 방법을 Diffusion Classifier라고 한다. Diffusion Classifier는 추가 학습 없이 사전 학습된 diffusion model에서 classifier를 추출하는 강력하고 hyperparameter 없는 접근 방식이다. Diffusion Classifier는 Stable Diffusion과 같은 text-to-image 모델에서 zero-shot classifier를 추출하거나 DiT와 같은 클래스 조건부 diffusion model에서 일반적인 classifier를 추출하는 데 사용할 수 있다.

2. Variance Reduction via Difference Testing

언뜻 보기에 각 클래스 $\textbf{c}$에 대해 \(\mathbb{E}_{t,\epsilon} [\| \epsilon - \epsilon_\theta (\textbf{x}_t, \textbf{c}) \|^2]\)를 정확하게 추정하려면 엄청나게 많은 샘플이 필요한 것처럼 보인다. 실제로 수천 개의 샘플을 사용하더라도 몬테카를로 추정치는 클래스를 신뢰할 수 있게 구분하기에 충분히 정확하지 않다. 그러나 중요한 것은 classification에는 예측 오차 간의 상대적인 차이만 필요하고 절대적인 크기는 필요하지 않다는 것이다. \(p_\theta (\textbf{c}_i \, \vert \, \textbf{x})\)의 근사를 다음과 같이 다시 쓸 수 있다.

\[\begin{equation} \frac{1}{\sum_j \exp (\mathbb{E}_{t,\epsilon} [\| \epsilon - \epsilon_\theta (\textbf{x}_t, \textbf{c}) \|^2 - \| \epsilon - \epsilon_\theta (\textbf{x}_t, \textbf{c}_j) \|^2])} \end{equation}\]

위 식은 각 조건 값에 대한 예측 오차의 차이만 추정하면 된다는 것을 분명히 보여준다. 실제로는 \((t_i, \epsilon_i)\)의 여러 랜덤 샘플을 사용하여 각 조건 입력 $\textbf{c}$에 대한 ELBO를 추정하는 대신 고정된 집합 \(S = \{(t_i, \epsilon_i)\}_{i=1}^N\)을 샘플링하고 동일한 샘플을 사용하여 모든 $\textbf{c}$에 대한 $\epsilon$-prediction error를 추정한다.

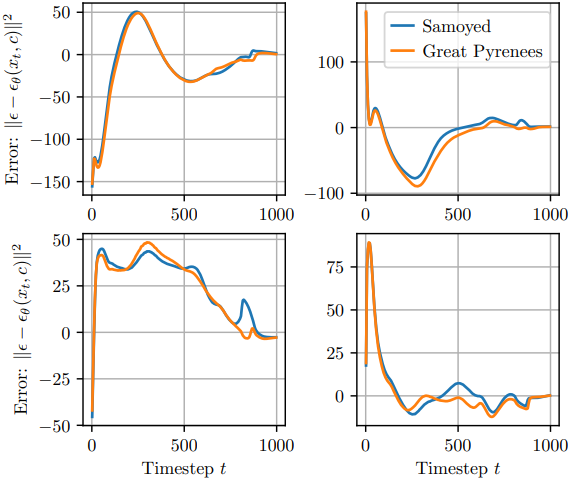
위 그림은 4개의 고정 \(\epsilon_i\), 모든 $t \in 1, \ldots, 1000$, 두 개의 프롬프트 (“Samoyed”, “Great Pyrenees”), 고정된 Great Pyrenees 입력 이미지에 대해 $\epsilon$-prediction error를 평가한 것이다. 고정된 프롬프트의 경우에도 $\epsilon$-prediction error는 사용된 \(\epsilon_i\)에 따라 크게 다르다. 그러나 각 프롬프트 간의 오차 차이는 각 \(\epsilon_i\)에 대해 훨씬 더 일관적이다. 따라서 동일한 \((t_i, \epsilon_i)\)를 사용하면 \(p_\theta (\textbf{c}_i \, \vert \, \textbf{x})\)에 대한 추정치가 훨씬 더 정확해진다.

Practical Considerations

1. Effect of timestep

\(p_\theta (\textbf{c}_i \, \vert \, \textbf{x})\)를 추정하기 위한 이론적 원칙적인 방법인 Diffusion Classifier는 $\epsilon$-prediction error를 추정하기 위해 timestep $t$에 대한 균일 분포를 사용한다. 여기서 저자들은 $t$에 대한 다른 분포가 더 정확한 결과를 산출하는지 확인하였다.

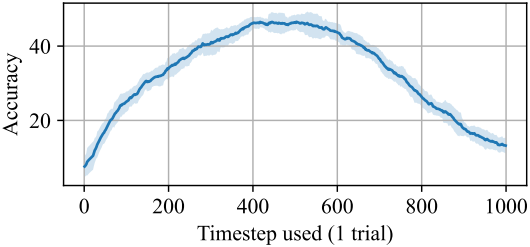
위 그림은 클래스마다 하나의 timestep 평가만 사용할 때의 Pets에서의 정확도이다. 직관적으로 보면 정확도는 중간 timestep을 사용할 때 가장 높다.

중간 timestep을 과다 샘플링하고 낮거나 높은 timestep을 과소 샘플링하여 정확도를 개선할 수 있을까?

저자들은 다양한 timestep 샘플링 전략을 시도하였다. 다른 전략 간의 trade-off는 여러 $\epsilon$으로 몇 개의 $t_i$를 반복적으로 시도할 것인지 아니면 여러 $t_i$를 한 번 시도할 것인지이다.

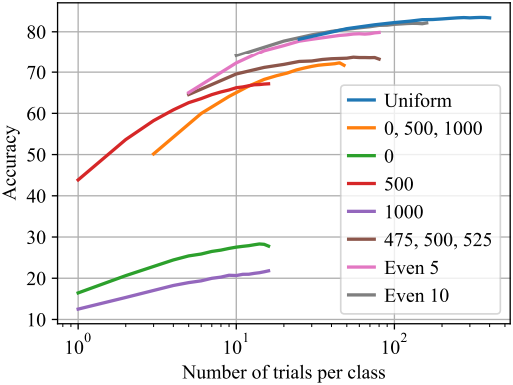
그림 4는 모든 전략이 더 많은 샘플의 평균 오차를 사용할 때 개선되지만, 단순히 균일한 간격의 timestep을 사용하는 것이 가장 좋다는 것을 보여준다. 저자들은 작은 $t_i$ 세트를 반복적으로 시도하는 것은 ELBO 추정치에 편향을 주기 때문에 스케일링이 좋지 않다고 가정하였다.

2. Efficient Classification

Naive한 구현은 주어진 이미지를 분류하기 위해 $C \times N$ 번의 시행이 필요하다. 여기서 $C$는 클래스 수이고 $N$은 각 조건부 ELBO를 추정하기 위해 평가할 $(t, \epsilon)$ 샘플 수이다. 그러나 더 나은 방법을 사용할 수 있다.

\(\arg \max_\textbf{c} \, p (\textbf{c} \, \vert \, \textbf{x}\)만 고려하므로 자신 있게 거부할 수 있는 클래스에 대한 ELBO 계산을 중단할 수 있다. 따라서 이미지를 분류하는 한 가지 옵션은 Upper Confidence Bound (UCB) 알고리즘을 사용하여 대부분의 계산을 최상위 후보에 할당하는 것이다. 그러나 이를 위해서는 \(\| \epsilon - \epsilon_\theta (\textbf{x}_t, \textbf{c}_j) \|^2\)의 분포가 timestep $t$에서 동일하다고 가정해야 하며 이는 성립하지 않는다.

저자들은 더 간단한 방법이 똑같이 잘 작동한다는 것을 발견했다. 평가를 일련의 단계로 나누었고, 각 단계에서 남은 각 $\textbf{c}_i$를 여러 번 시도한 다음 가장 높은 평균 오차를 갖는 것을 제거한다. 이를 통해 거의 확실히 최종 출력이 아닌 클래스를 효율적으로 제거하고 합리적인 클래스에 더 많은 컴퓨팅을 할당할 수 있다.

예를 들어, 2개의 단계로 Pets 이미지를 분류한다고 해보자. 첫 번째 단계에서는 각 클래스를 25번 시도한 다음 평균 오차가 가장 작은 5개 클래스만 남긴다. 두 번째 단계에서는 남은 5개 클래스를 각각 225번 더 시도한다. 이 평가 전략을 사용하면 RTX 3090 GPU에서 하나의 Pets 이미지를 분류하는 데 18초가 걸린다.

클래스가 많을 때는 inference가 여전히 실용적이지 않다. 1000개의 클래스가 있는 단일 ImageNet 이미지를 분류하는 데는 512$\times$512 해상도의 Stable Diffusion을 사용하여 약 1000초가 걸린다.

Experiments

1. Zero-shot Classification

다음은 zero-shot classification 성능을 비교한 표이다.

다음은 Stable Diffusion 2.0 데이터 필터링 과정 이후에 남게 되는 각 test set의 비율을 보여준다. (SFW: safe-for-work)

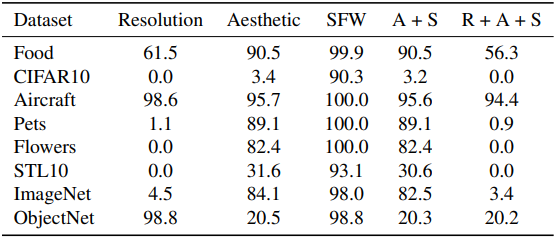
Zero-shot test set들 중 다수는 Stable Diffusion에 대하여 완전히 out-of-distribution임을 알 수 있다.

2. Improved Compositional Reasoning Abilities

다음은 Winoground 데이터셋에서의 compositional reasoning 성능을 비교한 표이다.

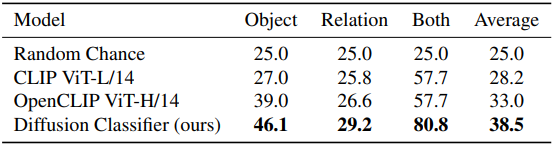
3. Supervised Classification

다음은 ImageNet에서의 일반적인 classification 성능을 비교한 표이다.

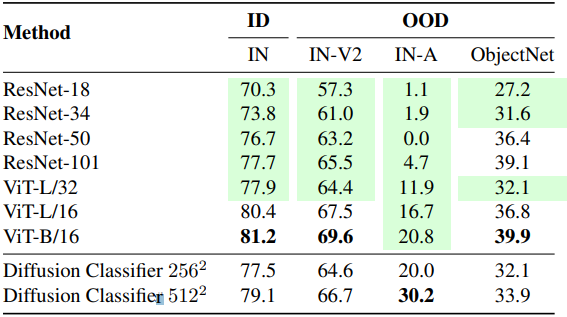
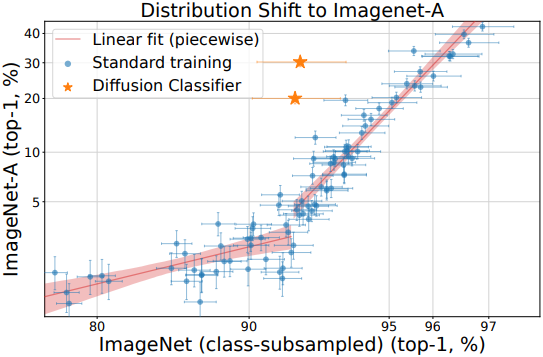
다음은 ImageNet-A (ResNet이 잘못 분류한 이미지로 만든 데이터셋)에 대한 일반화 성능을 비교한 그래프이다.

다음은 classification 목적 함수에 따른 효과를 비교한 표이다.