[논문리뷰] Diffusion-based Image Translation using Disentangled Style and Content Representation (DiffuseIT)

ICLR 2023. [Paper]
Gihyun Kwon, Jong Chul Ye
KAIST
30 Sep 2022

Introduction

Image translation은 모델이 입력 이미지를 받아 타겟 도메인으로 변환하는 task이다. 초기 image translation 접근 방식은 주로 단일 도메인 translation을 위해 설계되었지만 곧 다중 도메인 translation으로 확장되었다. 이러한 방법은 각 도메인에 대해 많은 학습 세트를 요구하기 때문에 멀티스케일 학습을 사용한 일대일 image translation 또는 패치 매칭 전략을 포함하여 단일 이미지 쌍만을 사용하는 image translation 접근 방식이 연구되었다. 가장 최근에 Splicing ViT는 사전 학습된 DINO ViT를 활용하여 입력 이미지의 구조를 유지하면서 주어진 이미지의 의미론적 모양을 타겟 도메인으로 변환한다.

한편, CLIP과 같은 최근의 텍스트-이미지 임베딩 모델을 사용하여 텍스트 프롬프트에 따라 이미지를 생성하려는 여러 접근 방식이 시도되었다. 이러한 방법은 backbone 생성 모델로 GAN에 의존하기 때문에 OOD(out-of-data) 이미지 생성에 적용될 때 semantic 변경이 적절하게 제어되지 않는 경우가 많다.

최근 score 기반 생성 모델은 텍스트 조건 이미지 생성에서 SOTA 성능을 보여주었다. 그러나 score 기반 모델에 여러 조건이 주어지는 image translation 시나리오의 경우 구성 요소를 분리하고 개별적으로 제어하는 것은 여전히 미해결 문제로 남아 있다.

실제로 diffusion model에 의한 image translation에서 가장 중요한 질문 중 하나는 입력 이미지의 구조 정보(또는 내용)를 유지하면서 semantic 정보(또는 스타일)만 변환하는 것이다. 일치하는 입력과 타겟 도메인 이미지로 학습된 조건부 diffusion model에서는 문제가 될 수 없지만 이러한 학습은 많은 image translation task에서 실용적이지 않다. 반면 unconditional diffusion model을 사용하는 기존의 방법은 semantic과 콘텐츠가 동시에 변하는 얽힘 문제 (entanglement problem)로 인해 콘텐츠 정보를 보존하지 못하는 경우가 많다. DiffusionCLIP은 DDIM과 pixel-wise loss를 사용하여 이 문제를 해결하려고 시도했지만 계산 비용이 많이 드는 새로운 타겟 도메인에 대해 score function을 fine-tuning해야 한다.

입력 이미지의 콘텐츠를 유지하면서 동시에 타겟 텍스트 또는 이미지의 semantic을 따르는 출력을 생성하는 방식으로 diffusion process를 제어하기 위해 사전 학습된 Vision Transformer (ViT)를 사용하여 loss function을 도입한다. 구체적으로, DINO ViT 모델에서 multi-head self-attention layer의 중간 key와 마지막 레이어의 classification 토큰을 추출하여 각각 콘텐츠 및 스타일 정규화로 사용한다. 구조적 정보를 보존하기 위해 샘플링 중에 입력의 중간 key와 denoise된 이미지 간의 similarity loss와 contrastive loss을 사용한다. 그런 다음 denoise된 샘플과 타겟 도메인 간의 토큰을 일치시켜 image guided style transfer가 수행되는 반면 텍스트 기반 style transfer에는 추가 CLIP loss가 사용된다. 샘플링 속도를 더욱 향상시키기 위해 새로운 semantic divergence loss와 리샘플링 전략을 사용한다.

Proposed Method

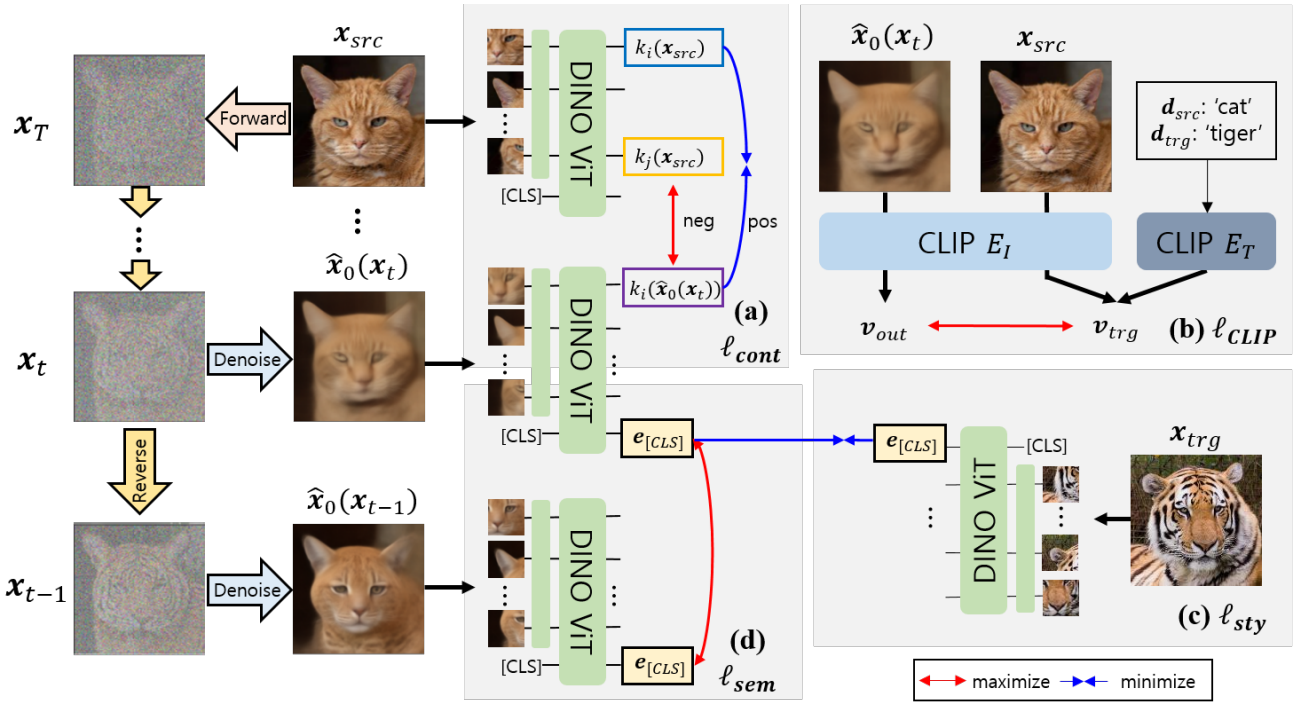
1. DDPM Sampling with Manifold Constraint

DDPM에서 깨끗한 이미지 $x_0 \sim q(x_0)$에서 시작하여 forward diffusion process $q(x_t \vert x_{t-1})$는 매 step $t$마다 점진적으로 Gaussian noise를 추가하는 Markov chain으로 설명된다.

\[\begin{equation} q(x_T \vert x_0) := \sum_{t=1}^T q(x_t \vert x_{t-1}), \\ \textrm{where} \quad q(x_t \vert x_{t-1}) := \mathcal{N} (x_t; \sqrt{1 - \beta_t} x_{t-1}, \beta_t I) \end{equation}\]

여기서 \(\{\beta_t\}_{t=0}^T\)는 분산 schedule이다. $x_t$는 다음과 같이 하나의 step으로 샘플링될 수 있다.

\[\begin{equation} x_t = \sqrt{\vphantom{1} \bar{\alpha}_t} x_0 + \sqrt{1 - \bar{\alpha}_t} \epsilon, \quad \textrm{where} \; \epsilon \sim \mathcal{N}(0, I) \end{equation}\]

Forward step $q(x_{t-1} \vert x_t)$의 reverse가 다루기 어렵기 때문에 DDPM은 파라미터 $\theta$를 사용하여 parameterize된 Gaussian transition $p_\theta (x_{t-1} \vert x_t)$를 통해 변동 하한(VLB)을 최대화하는 방법을 학습한다. 따라서 reverse process는 $p(x_T) \approx \mathcal{N}(x_T; 0, I)$에서 시작하여 학습된 평균과 고정 분산을 갖는 Markov chain으로 근사된다.

\[\begin{equation} p_\theta (x_{0:T}) := p_\theta (x_T) \prod_{t=1}^T p_\theta (x_{t-1} \vert x_t) \\ \textrm{where} \quad p_\theta (x_{t-1} \vert x_t) := \mathcal{N} (x_{t-1}; \mu_\theta (x_t, t), \sigma_t^2 I) \end{equation}\]

여기서 평균 $\mu_\theta (x_t, t)$는 다음과 같이 정의된다.

\[\begin{equation} \mu_\theta (x_t, t) := \frac{1}{\sqrt{\alpha_t}} \bigg( x_t - \frac{1 - \alpha_t}{\sqrt{1 - \bar{\alpha}_t}} \epsilon_\theta (x_t, t) \bigg) \end{equation}\]

여기서 $\epsilon_\theta (x_t, t)$는 다음과 같은 목적 함수로 학습된 diffusion model이다.

\[\begin{equation} L (\theta) := \mathbb{E}_{t, x_0, \epsilon} [\| \epsilon - \epsilon_\theta (\sqrt{\vphantom{1} \bar{\alpha}_t} x_0 + \sqrt{1 - \bar{\alpha}_t} \epsilon, t) \|^2 ] \end{equation}\]

최적화 후 학습된 score function을 reverse process에 연결하여 다음과 같이 $p_\theta (x_{t-1} \vert x_t)$에서 간단히 샘플링할 수 있다.

\[\begin{aligned} x_{t-1} &= \mu_\theta (x_t, t) + \sigma_t \epsilon \\ &= \frac{1}{\sqrt{\alpha_t}} \bigg( x_t - \frac{1 - \alpha_t}{\sqrt{1 - \bar{\alpha}_t}} \epsilon_\theta (x_t, t) \bigg) + \sigma_t \epsilon \end{aligned}\]

조건부 diffusion model을 사용하는 image translation에서 diffusion model $\epsilon_\theta$는

\[\begin{equation} \epsilon_\theta(y, \sqrt{\vphantom{1} \bar{\alpha}_t} x_0 + \sqrt{1 - \bar{\alpha}_t} \epsilon, t) \end{equation}\]

로 대체되어야 한다. 여기서 $y$는 일치하는 타겟 이미지를 나타낸다. 따라서 일치하는 타겟에 의해 supervised 방식으로 샘플 생성이 엄격하게 제어되므로 이미지 콘텐츠 변경이 거의 발생하지 않는다. 불행하게도 학습을 위한 일치하는 타겟의 요구 사항으로 인해 이 접근 방식은 비실용적이다.

이를 해결하기 위해 unconditional diffusion model 학습과 사전 학습된 classifier $p_\phi (y \vert x_t)$를 사용하는 classifier-guided image translation이 제안되었다. 구체적으로, $\mu_\theta (x_t, t)$는 classifier의 기울기, 즉

\[\begin{equation} \hat{\mu}_\theta (x_t, t) := \mu_\theta (x_t, t) + \sigma_t \nabla_{x_t} \log p_\phi (y \vert x_t) \end{equation}\]

로 보완된다. 그러나 별도로 학습되어야 하는 대부분의 classifier는 일반적으로 reverse process에서 샘플의 콘텐츠를 제어하기에 충분하지 않다.

저자들은 inverse problem에 대한 최근 Manifold Constrained Gradient (MCG)에서 영감을 받아 콘텐츠와 스타일 안내 문제를 inversse problem으로 공식화하였다. 이는 다음과 같은 샘플 $x$에 대한 총 비용 함수를 최소화하여 해결할 수 있다.

\[\begin{equation} \ell_\textrm{total} (x; x_\textrm{trg}, x_\textrm{src}), \quad \textrm{or} \quad \ell_\textrm{total} (x; d_\textrm{trg}, x_\textrm{src}, d_\textrm{src}) \end{equation}\]

여기서 $x_\textrm{src}$와 $x_\textrm{trg}$는 각각 소스 이미지와 타겟 이미지를 나타낸다. $d_\textrm{src}$와 $d_\textrm{trg}$는 각각 소스 텍스트와 타겟 텍스트를 나타낸다. $\ell_\textrm{total}$의 첫 번째 형식은 image-guided translation에 사용되며 두 번째 형식은 text-guided translation에 사용된다. 그러면 MCG를 사용한 reverse diffusion의 샘플링은 다음과 같다.

\[\begin{aligned} x'_{t-1} &= \frac{1}{\sqrt{\alpha_t}} \bigg( x_t - \frac{1 - \alpha_t}{\sqrt{1 - \bar{\alpha}_t}} \epsilon_\theta (x_t, t) \bigg) + \sigma_t \epsilon \\ x_{t-1} &= x'_{t-1} - \nabla_{x_t} \ell_\textrm{total} (\hat{x}_0 (x_t)) \end{aligned}\]

여기서 \(\hat{x}_0 (x_t)\)는 샘플 $x_t$에서 추정된 깨끗한 이미지이며, Tweedie’s formula를 사용하면 다음과 같이 구할 수 있다.

\[\begin{equation} \hat{x}_0 (x_t) := \frac{x_t}{\sqrt{\vphantom{1} \bar{\alpha}_t}} - \frac{\sqrt{1 - \bar{\alpha}_t}}{\sqrt{\vphantom{1} \bar{\alpha}_t}} \epsilon_\theta (x_t, t) \end{equation}\]

2. Structure Loss

앞에서 언급했듯이 image translation의 주요 목적은 출력과 입력 이미지 사이의 콘텐츠 구조를 유지하면서 출력이 타겟 조건의 semantic을 따르도록 가이드하는 것이다. 기존 방법은 콘텐츠 보존을 위해 pixel-wise loss 또는 perceptual loss를 사용한다. 그러나 픽셀 space는 콘텐츠와 semantic 구성 요소를 명시적으로 구별하지 않는다. 너무 강한 pixel loss는 출력의 semantic 변화를 방해하는 반면, 약한 pixel loss는 semantic 변화와 함께 구조적 구성 요소를 변경한다. 이 문제를 해결하기 위해서는 이미지의 semantic 정보와 구조 정보를 별도로 처리해야 한다.

최근 연구는 사전 학습된 DINO ViT를 사용하여 두 구성 요소를 성공적으로 분리하였다. 그들은 ViT에서 multi-head self-attention (MSA) layer의 키 $k^l$이 구조 정보를 포함하고 마지막 레이어의 토큰이 semantic 정보를 포함함을 보여주었다. 위의 feature들을 통해 key의 self-similarity 행렬 $S^l$을 일치시켜 입력과 네트워크 출력 사이의 구조를 유지하기 위한 loss를 제안했으며, 이는 본 논문의 문제에 대해 다음 형식으로 나타낼 수 있다.

\[\begin{equation} \ell_\textrm{ssim} (x_\textrm{src}, x) = \| S^l (x_\textrm{src}) - S^l (x) \|_F \\ \textrm{where} \quad [S^l (x)]_{i, j} = \cos (k_i^l (x), k_j^l (x)) \end{equation}\]

여기서 $k_i^l (x)$와 $k_j^l (x)$는 이미지 $x$를 사용하여 ViT에서 추출한 $l$ 번째 MSA 레이어의 $i$, $j$ 번째 key를 나타낸다. Self-similarity loss는 입력과 출력 사이의 콘텐츠 정보를 유지할 수 있지만 이 loss만 사용하면 DDPM 프레임워크에서 정규화가 약해진다. Key $k_i$에는 $i$번째 패치 위치에 해당하는 공간적 정보가 포함되어 있으므로 관계 일관성과 contrastive learning을 모두 사용한다는 아이디어에서 영감을 받아 contrastive learning과 함께 추가 정규화를 사용한다. 구체적으로, patch contrastive loss의 아이디어를 활용하여 DINO ViT key들을 사용하여 infoNCE 손실을 정의한다.

\[\begin{equation} \ell_\textrm{cont} (x_\textrm{src}, x) = - \sum_i \log \bigg( \frac{\exp (\textrm{sim} (k_i^l (x), k_i^l (x_\textrm{src})) / \tau)}{\exp (\textrm{sim} (k_i^l (x), k_i^l (x_\textrm{src})) / \tau) + \sum_{j \ne i} \exp (\textrm{sim} (k_i^l (x), k_j^l (x_\textrm{src})) / \tau)} \bigg) \end{equation}\]

여기서 $\tau$는 temperature이고 $\textrm{sim} (\cdot, \cdot)$은 정규화된 cosine similarity이다. 이 loss로 동일한 위치의 key를 정규화하여 더 가까운 거리를 갖도록 하고 다른 위치의 key 사이의 거리를 최대화한다.

3. Style Loss

CLIP Loss for Text-guided Image Translation

사전 학습된 CLIP 모델을 사용하여 reverse diffusion을 유도하기 위해 제안된 CLIP-guided diffusion은 다음 loss function을 사용한다.

\[\begin{equation} \ell_\textrm{CLIP} (d_\textrm{trg}, x) := - \textrm{sim} (E_T (d_\textrm{trg}), E_I (x)) \end{equation}\]

여기서 $d_\textrm{trg}$는 타겟 텍스트 프롬프트이고, $E_I$와 $E_T$는 각각 CLIP의 이미지 인코더와 텍스트 인코더를 뜻한다. 이 loss가 diffusion model에게 텍스트 guidance를 줄 수 있음에도 불구하고 결과 이미지의 품질이 좋지 않다.

대신 $d_\textrm{trg}$, $d_\textrm{src}$, $x_\textrm{src}$ 측면에서 출력 이미지의 CLIP 임베딩을 타겟 벡터와 일치시키는 input-aware directional CLIP loss를 사용할 것을 제안한다. 보다 구체적으로 CLIP 기반 semantic loss은 다음과 같이 설명된다.

\[\begin{equation} \ell_\textrm{CLIP} (x; d_\textrm{trg}, x_\textrm{src}, d_\textrm{src}) := - \textrm{sim} (v_\textrm{trg}, v_\textrm{src}) \\ v_\textrm{trg} := E_T (d_\textrm{trg}) + \lambda_i E_I (x_\textrm{src}) - \lambda_s E_T (d_\textrm{src}) \\ v_\textrm{src} := E_I (\textrm{aug} (x)) \end{equation}\]

여기서 $\textrm{aug} (\cdot)$은 CLIP에서 발생하는 적대적 아티팩트를 방지하기 위한 augmentation이다. 소스 도메인 정보를 제거함과 동시에 소스 이미지 정보를 반영하여 $\lambda_s$와 $\lambda_i$의 값에 따라 출력한다. 따라서 기존 loss를 사용하는 것에 비해 안정적인 출력을 얻을 수 있다.

또한 사전 학습된 단일 CLIP 모델 (ex. ViT/B-32)만을 사용하는 기존 방법과 달리 최근 제안된 CLIP 모델 앙상블 방법을 사용하여 텍스트-이미지 임베딩 성능을 향상시킨다. 특히, 단일 임베딩을 사용하는 대신 사전 학습된 여러 CLIP 모델의 여러 임베딩 벡터를 연결하고 이를 최종 임베딩으로 사용한다.

Semantic Style Loss for Image-guided Image Translation

Image-guide translation의 경우 ViT의 토큰을 스타일 guidance로 사용한다. 토큰에는 이미지의 semantic 스타일 정보가 포함된다. 따라서 토큰 거리를 최소화하여 샘플의 semantic을 타겟 이미지의 semantic과 일치시키는 diffusion process를 가이드할 수 있다. 또한 토큰만 사용하면 색상 값이 잘못 정렬되는 경우가 많다. 이를 방지하기 위해 이미지 간 MSE loss각 약한 타겟 이미지의 전체 색상 통계를 따르도록 출력을 가이드한다. 따라서 loss function은 다음과 같다.

\[\begin{equation} \ell_\textrm{sty} (x_\textrm{trg}, x) = \| e_\textrm{[CLS]}^L (x_\textrm{trg}) - e_\textrm{[CLS]}^L (x) \|_2 + \lambda_\textrm{mse} \| x_\textrm{trg} - x \|_2 \end{equation}\]

여기서 \(e_\textrm{[CLS]}^L\)은 마지막 레이어의 [CLS] 토큰이다.

4. Acceleration Strategy

Semantic Divergence Loss

제안된 loss function을 사용하여 텍스트 또는 이미지 가이드 image translation 출력을 얻을 수 있다. 그러나 원하는 출력에 도달하려면 생성 프로세스에 큰 step이 필요하다. 본 논문은 이 문제를 해결하기 위해 diffusion process를 가속화하는 간단한 접근 방식을 제안한다. 앞에서 설명한 것처럼 ViT의 토큰에는 이미지의 전체적인 semantic 정보가 포함되어 있다. 구조를 유지하면서 semantic 정보를 원본과 최대한 다르게 만드는 것이 목적이므로 생성 프로세스에서 이전 step의 토큰과 현재 출력 간의 거리를 최대화하여 원하는 목적을 달성할 수 있다. 따라서 시간 $t$에서의 loss function은 다음과 같다.

\[\begin{equation} \ell_\textrm{sem} (x_t; x_{t+1}) = - \| e_{[CLS]}^L (\hat{x}_0 (x_t)) - e_{[CLS]}^L (\hat{x}_0 (x_{t+1})) \|_2 \end{equation}\]

구체적으로, 현재 시간과 이전 시간의 denoise된 출력 사이의 거리를 최대화하여 다음 step 샘플이 이전 step과 다른 semantic을 갖도록 한다. Pixel-wise 거리 또는 perceptual 거리를 최대화하기 위한 대안을 생각할 수 있지만 이러한 경우 콘텐츠 구조가 크게 손상된다. 그에 반해 제안한 loss는 semantic 모양만 제어할 수 있기 때문에 이미지 품질 측면에서 장점이 있다.

Resampling Strategy

CCDF 가속 전략에서 볼 수 있듯이 더 나은 초기화는 inverse problem에 대한 가속된 reverse diffusion으로 이어진다. 경험적으로 image translation 문제에서 reverse diffusion에 대한 timestep $T$에서 좋은 시작점을 찾는 것이 전체 이미지 품질에 영향을 미친다. 구체적으로, 초기 추정치 $x_T$가 충분히 좋도록 가이드하기 위해, 다음 step을 위한 기울기가 loss에 의해 쉽게 영향 받는 $x_T$를 찾기 위해

\[\begin{equation} x_T = \sqrt{1 - \beta_{T-1}} x_{T-1} + \sqrt{\beta_{T-1}} \epsilon \end{equation}\]

의 forward step이 뒤따르는 하나의 reverse sampling $x_{T −1}$의 $N$번의 iteration을 수행한다. 다음 step의 기울기는 loss에 의해 쉽게 영향을 받는다. 이 초기 리샘플링 전략을 통해 경험적으로 reverse step의 수를 줄일 수 있는 초기 $x_T$를 찾을 수 있다.

5. Total Loss

모두 종합하면 text-guided reverse diffusion의 최종 loss는 다음과 같다.

\[\begin{equation} \ell_\textrm{total} = \lambda_1 \ell_\textrm{cont} + \lambda_2 \ell_\textrm{ssim} + \lambda_3 \ell_\textrm{CLIP} + \lambda_4 \ell_\textrm{sem} + \lambda_5 \ell_\textrm{rng} \end{equation}\]

여기서 \(\lambda_\textrm{rng}\)는 reverse process의 불규칙한 step을 방지하기 위한 정규화 loss이다. 텍스트 조건 $d_\textrm{src}$와 $d_\textrm{trg}$ 대신 타겟 스타일 이미지 $x_\textrm{trg}$가 제공된 경우 $\ell_\textrm{CLIP}$은 단순히 $\ell_\textrm{sty}$를 대체한다.

Experiment

• 구현 디테일
  • Blended Diffusion의 공식 소스코드를 참조
  • 모든 실험은 ImageNet 256$\times$256에서 사전 학습된 unconditional score model을 사용
  • Diffusion step $T = 60$ + 리샘플링 반복 $N = 10$ = 총 70 reverse step
  • 생성 프로세스는 1개의 RTX 3090에서 이미지당 40초 소요
  • $\ell_\textrm{CLIP}$에서 5개의 사전 학습된 CLIP 모델 사용

1. Text-guided Semantic Image Translation

다음은 동물 데이터셋에서의 text-guided translation을 정성적으로 비교한 결과이다.

다음은 풍경 데이터셋에서의 text-guided translation을 정성적으로 비교한 결과이다.

다음은 다양한 데이터셋에서의 text-guided translation을 정량적으로 비교한 결과이다.

2. Image-guided Semantic Image Translation

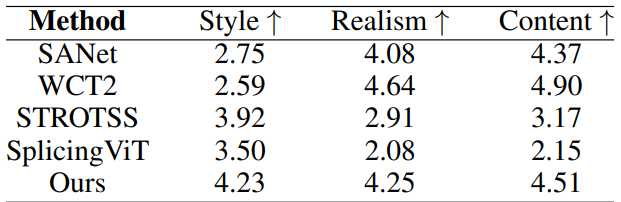
다음은 image-guided translation에 대한 user study 결과이다.

다음은 image-guided translation을 정성적으로 비교한 결과이다.

3. Ablation Study

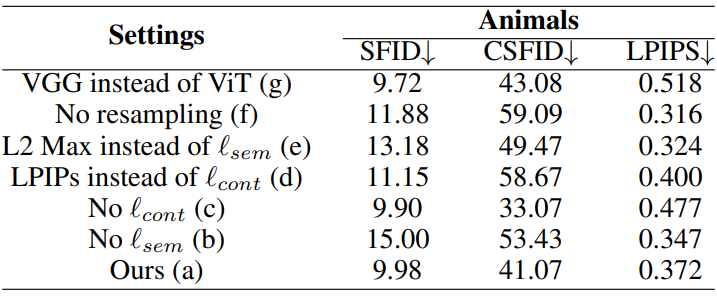
다음은 ablation study 결과이다.

• (a) DiffuseIT (Best Setting)
• (b) $\ell_\textrm{sem}$ 제거
• (c) $\ell_\textrm{cont}$ 제거
• (d) $\ell_\textrm{cont}$ 대신 LPIPS perceptual loss 사용
• (e) $\ell_\textrm{sem}$ 대신 pixel-wise $l_2$ loss 사용
• (f) 리샘플링 전략 제거
• (g) DINO ViT 대신 VGG16을 사용