[논문리뷰] Training-free Style Transfer Emerges from h-space in Diffusion models (DiffStyle)
arXiv 2023. [Paper] [Page] [Github]
Jaeseok Jeong, Mingi Kwon, Youngjung Uh
Yonsei University
27 Mar 2023

Introduction
Diffusion model(DM)은 랜덤 생성에서 뛰어난 성능으로 인해 다양한 도메인에서 인정을 받았다. Text-to-image DM은 classifier-free guidance를 사용하여 다양한 이미지를 생성하기 위해 주어진 텍스트를 반영하는 방법을 제공한다. 같은 맥락에서 image guidance는 guidance를 위해 주어진 레퍼런스 이미지와 유사한 랜덤 이미지를 합성한다. 이러한 접근 방식은 일부 제어를 제공하지만 생성 프로세스는 장면의 지정되지 않은 측면에서 여전히 랜덤성을 유지한다.
한편, ODE 샘플러와 같은 deterministic DM은 대부분의 원본 이미지를 보존하면서 실제 이미지를 편집하는 데 사용되었다. DiffusionCLIP과 Imagic은 먼저 입력 이미지를 noise에 포함하고 편집을 위해 DM을 fine-tuning한다. 여전히 fine-tuning된 DM은 각각 단일 속성 변경 또는 단일 이미지로 제한된다. DM의 중간 feature에 대한 통찰력을 제공하지 않는다.
최근 Asyrp는 $h$-space라는 U-Net의 bottleneck에 위치한 사전 학습된 DM의 숨겨진 latent space를 발견했다. Latent feature map을 특정 방향으로 이동하면 미소를 추가하는 것과 같은 semantic 속성 변경이 가능하다. Deterministic inversion과 결합하면 사전 학습된 고정 DM을 사용하여 실제 이미지 조작이 가능하다. 그러나 그 적용은 특정 속성을 변경하는 것으로 제한되며 feature map 교체와 같은 GAN에서와 같이 명시적인 연산을 제공하지 않는다.
저자들은 U-Net의 bottleneck feature가 콘텐츠를 포함하고 skip connection이 스타일을 전달한다는 것을 발견했다. 본 논문은 콘텐츠 이미지와 스타일 이미지가 주어지면 콘텐츠 주입을 위한 새로운 생성 프로세스를 설계한다. 도메인 내 스타일 이미지를 사용하면 style mixing과 같은 결과가 생성되는 반면 style transfer 연구의 외부 이미지를 사용하면 harmonization과 같은 효과가 생성된다.
DiffStyle이라는 본 논문의 방법은 $h$-space에 있는 콘텐츠 이미지의 중간 feature를 스타일 이미지의 $x_T$와 생성 프로세스로 혼합한다. Skip connection과 주입에 따른 조합 사이의 상관 관계를 유지하는 적절한 정규화를 feature와 점진적으로 결합한다.
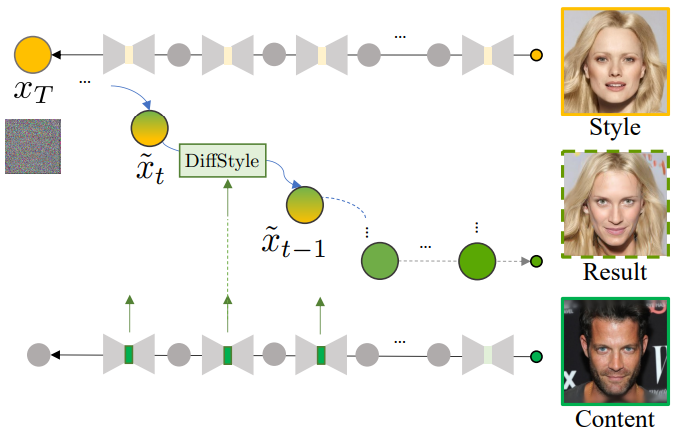
위 그림은 DiffStyle의 개요를 보여준다. 또한 콘텐츠를 보존하면서 스타일 요소를 더 잘 반영하도록 생성 프로세스를 보정한다.
DiffStyle은 사전 학습된 unconditional diffusion model을 사용하여 콘텐츠 주입을 가능하게 한다. Bottleneck이 공간 차원을 가진다는 점을 고려하면 타겟 영역 마스크와 함께 DiffStyle을 적용하면 로컬한 style mixing이 발생한다. DiffStyle은 추가 학습이나 추가 네트워크 없이 이러한 애플리케이션을 다루는 첫 번째 방법이다. 사용자가 기존의 사전 학습된 DM을 실험할 수 있는 편의성을 제공한다.
Preliminary
1. Denoising Diffusion Implicit Model (DDIM)
Diffusion model은 $\epsilon_t^\theta$와 일치하는 denoising score를 추정하여 데이터 분포를 학습한다. DDPM에서 forward process는 parameterize된 Gaussian transition을 통해 데이터를 확산시키는 Markov process로 정의된다. DDIM은 DDPM을
\[\begin{equation} q_\sigma (x_{t-1} \vert x_t, x_0) = \mathcal{N} \bigg( \sqrt{\alpha_{t-1}} x_0 + \sqrt{1 - \alpha_{t-1} - \sigma_t^2} \cdot \frac{x_t - \sqrt{\alpha_t} x_0}{\sqrt{1 - \alpha_t}}, \sigma_t^2 I \bigg) \\ \textrm{where} \quad \alpha_t = \prod_{s=1}^t (1 - \beta_s) \end{equation}\]로 재정의한다. 여기서 \(\{\beta_t\}_{t=1}^T\)는 분산 schedule이다. 따라서 reverse process는 다음과 같다.
\[\begin{aligned} x_{t-1} =\;& \sqrt{\alpha_{t-1}} \underbrace{\bigg( \frac{x_t - \sqrt{1 - \alpha_t} \epsilon_t^\theta (x_t)}{\sqrt{\alpha_t}} \bigg)}_{\textrm{predicted } x_0} \\ &+ \underbrace{\sqrt{1 - \alpha_{t-1} - \sigma_t^2} \cdot \epsilon_t^\theta (x_t)}_{\textrm{direction pointing to } x_t} + \underbrace{\sigma_t z_t}_{\textrm{random noise}} \\ \sigma_t =\;& \eta \sqrt{\frac{1 - \alpha_{t-1}}{1 - \alpha_t}} \sqrt{1 - \frac{\alpha_t}{\alpha_{t-1}}} \end{aligned}\]$\eta = 0$일 때 프로세스는 deterministic해진다.
2. Asymmetric reverse process (Asyrp)
Asyrp는 $h$-space를 semantic latent space로 사용하기 위한 비대칭 reverse process를 도입한다. $h$-space는 latent 변수 $x_t$와 구별되는 U-Net의 bottleneck이다. 실제 이미지 편집을 위해 DDIM forward process를 통해 $x_0 \sim p_\textrm{real}(x)$를 $x_T$로 반전시키고, 수정된 DDIM reverse process에서 새로운 $\tilde{h}_t$를 이용하여 $\tilde{x}_0$를 생성한다. Asyrp 논문에서는 DDIM reverse process를 다음과 같이 약식으로 표기하며, 본 논문 전체에서 이 표기법을 따른다.
\[\begin{equation} x_{t-1} = \sqrt{\alpha_{t-1}} P_t (\epsilon_t^\theta (x_t)) + D_t (\epsilon_t^\theta (x_t)) + \sigma_t z_t \end{equation}\]여기서 $P_t (\epsilon_t^\theta (x_t))$는 예측된 $x_0$이고 $D_t (\epsilon_t^\theta (x_t))$는 $x_t$를 가리키는 방향이다. 컨텍스트에서 argument를 명확하게 지정하는 경우 $P_t (\epsilon_t^\theta (x_t))$를 $P_t$로, $D_t (\epsilon_t^\theta (x_t))$를 $D_t$로 줄여서 쓴다. Asyrp에 따르면 $\eta = 0$일 때 $\sigma_t z_t$를 생략한다. 그러면 Asyrp은
\[\begin{equation} \tilde{x}_{t-1} = \sqrt{\alpha_{t-1}} P_t (\epsilon_t^\theta (\tilde{x}_t \vert \tilde{h}_t)) + D_t (\epsilon_t^\theta (\tilde{x}_t \vert \tilde{h}_t)) + \sigma_t z_t \end{equation}\]이 된다. 여기서 $\tilde{x}_T = x_T$이고 $\epsilon_t^\theta (\tilde{x}_t \vert \tilde{h}_t)$는 원래 U-Net feature map $h_t$를 $\tilde{h}_t$로 대체한다. $P_t$와 $D_t$ 모두에서 $h$-space의 수정이 결과에 무시할만한 변화를 가져온다고 한다. 따라서 Asyrp의 핵심 아이디어는 $D_t$를 보존하면서 $P_t$의 $h$-space만 수정하는 것이다.
Asyrp에 의해 도입된 품질 부스팅은 이미지가 거의 결정되었을 때 확률적 noise 주입이다. 이미지의 아이덴티티를 유지하면서 미세한 디테일을 향상시키고 이미지의 noise를 줄인다. Asyrp의 전체 프로세스는 다음과 같다.
\[\begin{equation} \tilde{x}_{t-1} = \begin{cases} \sqrt{\alpha_{t-1}} P_t (\epsilon_t^\theta (\tilde{x}_t \vert \tilde{h}_t)) + D_t & \quad \textrm{if } T \ge t \ge t_\textrm{edit} \\ \sqrt{\alpha_{t-1}} P_t (\epsilon_t^\theta (\tilde{x}_t \vert h_t)) + D_t & \quad \textrm{if } t_\textrm{edit} \ge t \ge t_\textrm{boost} \\ \sqrt{\alpha_{t-1}} P_t (\epsilon_t^\theta (\tilde{x}_t \vert h_t)) + D_t + \sigma_t^2 z & \quad \textrm{if } t_\textrm{boost} \ge t \end{cases} \end{equation}\]전체 프로세스는 편집 간격, denoising 간격, 품질 부스팅 간격으로 구성되며, hyperparameter $t_\textrm{edit}$가 편집 간격을 결정하고 $t_\textrm{boost}$가 품질 부스팅 간격을 결정한다.
Method
1. Role of $h$-space
DM에서 U-Net의 가장 깊은 bottleneck인 $h$-space는 결과 이미지의 의미를 어느 정도 포함한다. 즉, Asyrp로 $h$-space를 변경하면 결과 이미지를 편집하게 된다. $t \in [T, t_\textrm{edit}]$에 대해 $\tilde{h}_t = h_t + \Delta h_t$를 설정하면 semantic이 수정된다. 여기서 $\Delta h_t$는 원하는 속성의 방향이다. Reverse process는
\[\begin{equation} \tilde{x}_{t-1} = \sqrt{\alpha_{t-1}} P_t (\epsilon_t^\theta (\tilde{x}_t \vert \tilde{h}_t)) + D_t (\epsilon_t^\theta (\tilde{x}_t \vert h_t)) \\ \tilde{h}_t = h_t + \Delta h_t^\textrm{attr} \end{equation}\]가 된다. 다음과 같은 질문에서 시작한다.
$h$는 GAN의 latent code에서와 같이 결과 이미지의 semantic을 단독으로 지정하는가?
즉, $h$를 교체하면 출력이 완전히 변경되는가?
이 질문에 답하기 위해 forward process를 통해 두 개의 이미지 $I^{(1)}$와 $I^{(2)}$를 noise $x_T^{(1)}$와 $x_T^{(2)}$로 각각 반전시킨다. 그런 다음 reverse process 중에 $x_T^{(1)}$의 \(\{h_t\}\)를 $x_T^{(2)}$의 \(\{h_t^{(2)}\}\)로 바꾼다.
\[\begin{aligned} \tilde{x}_T &= x_T^{(1)} \\ \tilde{x}_t &= \sqrt{\alpha_{t-1}} P_t (\epsilon_t^\theta (\tilde{x}_t \vert h_t^{(2)})) + D_t (\epsilon_t^\theta (\tilde{x}_t \vert h_t)) \end{aligned}\]
흥미롭게도 교체가 적용된 결과 이미지에는 위 그림과 같이 색상 분포와 배경과 같은 $I^{(1)}$의 일부 스타일 요소와 함께 $I^{(2)}$의 사람들이 포함된다. 이 현상은 주요 콘텐츠가 $h$로 지정되고 다른 측면은 skip connection의 feature와 같은 다른 구성 요소에서 비롯된다. 이제부터는 $h_t^{(2)}$를 $h_t^\textrm{content}$로 명명한다.
그러나 교체로 인해 이미지가 심하게 왜곡된다. Asyrp는 작은 변화 $\Delta h_t$로 $h_t$를 약간 조정한다. 반면에 $h_t$를 $h_t^\textrm{content}$로 교체하면 $h_t$가 완전히 제거된다. 저자들은 $h_t$의 유지가 핵심 요소일 수 있다고 가정하고 중간에 $h_t^\textrm{content}$를 $h_t$에 추가하였다. 그 결과 왜곡이 덜 발생한다. 이러한 예비 실험을 통해 저자들은 교체 및 추가가 feature map의 고유한 상관 관계를 방해한다는 가설을 세웠다.
2. Preserving statistics with Slerp
DM에서 $h$-space는 skip connection과 연결되어 다음 레이어로 공급된다. 생성 프로세스 내에서 $h_t$와 일치하는 skip connection $g_t$ 사이의 흥미로운 관계를 관찰하고 $h_t$를 교체하기 위한 요구 사항을 도입한다. $\vert h_t \vert$와 $\vert g_t \vert$ 사이의 상관 관계의 두 가지 버전을 계산한다.
\[\begin{equation} r_\textrm{homo} = \frac{\Sigma_i (| h^{(i)} | - | \bar{h} |)(| g^{(i)} | - | \bar{g} |)}{(n-1) s_{|h|} s_{|g|}} \\ r_\textrm{hetero} = \frac{\Sigma_{j \ne i} (| h^{(j)} | - | \bar{h} |)(| g^{(i)} | - | \bar{g} |)}{(n-1) s_{|h|} s_{|g|}} \end{equation}\]여기서 $n$은 샘플 수이며, $s$는 표준 편차이다. 간결함을 위해 $t$는 생략되었다.
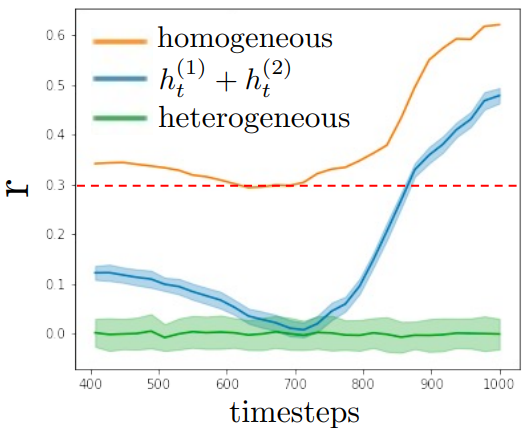
위 그림은 $r_\textrm{homo}$가 대략 0.3보다 크고 timestep이 $T$에 가까울 때 강한 양의 값임을 보여준다. 반면, $r_textrm{hetero}$는 0 근처에 있다. 또한 중간 프로세스는 $\tilde{h} = h^{(i)} + h^{(j)}$를 설정하여 $r_\textrm{alt}$를 $r_\textrm{homo}$에 더 가깝게 만들고 왜곡을 줄인다.
따라서 저자들은 생성된 이미지의 품질을 유지하려면 수정 후에도 $\vert h \vert$와 $\vert g \vert$ 사이의 상관관계를 유지해야 한다고 가설을 세웠다. 가설을 충족하고 $r_\textrm{alt}$와 $r_\textrm{homo}$ 사이의 가장 가까운 차이를 달성하기 위해 $h_t$와 $h_t^\textrm{content}$ 사이에 정규화된 spherical interpolation (Slerp)을 도입한다.
\[\begin{equation} \tilde{h}_t = f (h_t, h_t^\textrm{content}, \gamma) = \textrm{Slerp} \bigg(h_t, \frac{h_t^\textrm{content}}{\| h_t^\textrm{content} \|} \cdot \| h_t \|, \gamma \bigg) \end{equation}\]여기서 $\gamma \in [0, 1]$은 $h_t^\textrm{content}$의 계수이다. Slerp는 입력이 동일한 norm을 갖도록 요구한다. $h_t$의 norm과 일치하도록 $h_t^\textrm{content}$를 정규화하면 $\vert \textrm{Slerp}(\cdot) \vert$와 $\vert g_t^{(1)} \vert$ 사이의 상관관계가 $\vert h_t \vert$와 $\vert g_t^{(1)} \vert$ 사이의 상관관계와 같게 보장한다. Slerp를 사용하여 $h_t$를 $\tilde{h}_t$로 교체하면 아래 그림과 같이 더 적은 아티팩트와 더 나은 콘텐츠 보존이 나타난다.

개선 외에도 Slerp의 파라미터 $\gamma_t$를 통해 $h_t$와 $h_t^\textrm{content}$의 비율을 조정하여 얼마나 많은 콘텐츠를 주입할지 제어할 수 있다.
3. Style calibration
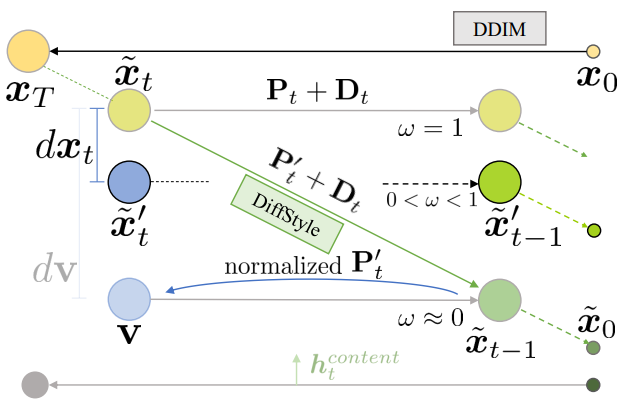
Slerp를 사용하여 $h$-space를 수정하면 대부분 원본 이미지의 스타일이 유지되지만 $h$-space에 대한 모든 변경 사항은 필연적으로 다음 denoising step $t-1$의 skip connection에 영향을 미치므로 스타일 구성 요소가 부분적으로 손실된다. 따라서 본 논문은 $\tilde{x}_t$를 조정하여 skip connection의 변화를 보상하는 style calibration을 제안한다.
Style calibration의 목표는 주입된 결과로 원래 스타일을 더 잘 보존하는 $\tilde{x}’_{t-1}$을 생성하는 것이다. 주입에 의해 유사한 변화를 가져오는 $\tilde{x}_t$에서 $\tilde{x}’_t$로의 암시적 변화를 모델링하고 변화의 강도를 제어하는 hyperparameter $\omega$를 도입한다. 이를 위해 slack 변수 $v = x_t + dv$를 정의하고
\[\begin{equation} P_t(\epsilon_t^\theta (v)) \approx P_t (\epsilon_t^\theta (x_t \vert \tilde{h}_t)) \end{equation}\]가 되는 $d_v$를 찾는다. DDIM 방정식
\[\begin{equation} \sqrt{\alpha_t} P_t = x_t - \sqrt{1 - \alpha_t} \epsilon_t^\theta (x_t) \end{equation}\]에서 극소를 다음과 같이 정의할 수 있다.
\[\begin{equation} \sqrt{\alpha_t} dP_t = dx_t - \sqrt{1 - \alpha_t} J (\epsilon_t^\theta) dx_t \end{equation}\]추가로 $dx_t = \omega dv$이고 $J (\epsilon_t^\theta) dv = d \epsilon_t^\theta$라고 하면 다음을 유도할 수 있다.
\[\begin{equation} dx_t = \sqrt{\alpha_t} dP_t + \omega \sqrt{1 - \alpha_t} d \epsilon_t^\theta \end{equation}\]그러면 $\tilde{x}’_t = \tilde{x}_t + dx_t$라 정의하고 $\tilde{x}’_t$를 denoising step으로 얻는다.
또한, $P_t (\epsilon_t^\theta (\tilde{x}’_t))$는 $P_t (\epsilon_t^\theta (\tilde{x}_t))$보다 표준편차가 크다. 다음과 같이 $P_t (\epsilon_t^\theta (\tilde{x}’_t))$의 동일한 표준 편차를 갖도록 정규화한다.
\[\begin{equation} dP_t = \frac{P'_t - \bar{P'}_t}{| P'_t |} | P_t | + \bar{P'}_t - P_t (\epsilon_t^\theta (\tilde{x}_t)) \\ \textrm{where} \quad P'_t = P_t (\epsilon_t^\theta (\tilde{x}'_t)) \end{equation}\]그런 다음 $\omega$로 $x’_t$를 제어한다.
$dx_t$를 더 확장하면 다음과 같다.
\[\begin{equation} dx_t \approx (\omega - 1) \sqrt{1 - \alpha_t} (\epsilon_t^\theta (\tilde{x}_t \vert \tilde{h_t}) - \epsilon_t^\theta (\tilde{x}_t)) \end{equation}\]흥미롭게도 $\omega = 1$로 설정하면 $dx_t$가 0으로 감소한다. 즉, 주입이 발생하지 않는다. 그리고 $\omega \approx 0$로 설정하면 \(\tilde{x}'_{t-1}\)이 \(\tilde{x}_{t-1}\)에 가까워진다. 즉, style calibration이 발생하지 않는다. 직관적으로, $x’_t$는 예측된 $x_0$를 $P_t (\epsilon_t^\theta (\tilde{x}_t \vert \tilde{h}_t))$와 공유할 수 있고 스타일 요소를 포함할 수 있다. 즉, $h$-space에서 콘텐츠 주입을 수행하는 동안 $x$-space에서 직접 $dx_t$를 추가하여 스타일 요소를 유지한다.
Style calibration은 네 단계로 구성된다.
- 콘텐츠를 \(\tilde{x}_t \rightarrow \tilde{x}_{t-1}\)로 주입한다.
- 주입 후 원래 신호 분포를 보존하기 위해 $P_t$를 정규화한다.
- DDIM 방정식 \(\tilde{x}'_t = \tilde{x}_t + dx_t\)를 푼다.
- \(\tilde{x}'_t \rightarrow \tilde{x}'_{t-1}\)의 reverse process를 진행한다.
4. Content injection and style transfer
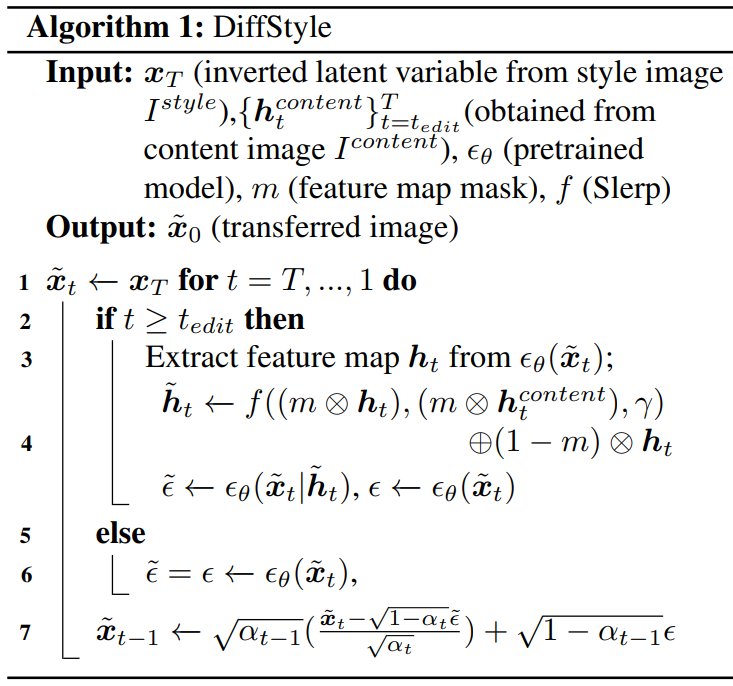
$h$-space는 콘텐츠를 포함하고 $x_T$에서 skip connection이 스타일 요소를 지정한다. 콘텐츠 주입 및 style transfer에 이 현상을 활용한다. 랜덤한 실제 이미지에서 $x_T$를 얻을 수 있다. 따라서 예술적 이미지와 같은 도메인 외부 이미지를 사용하더라도 DiffStyle은 이미지의 스타일을 성공적으로 전송한다. 또한 $h$-space의 공간적 혼합은 해당 타겟 영역에 콘텐츠를 주입하여 로컬 style mixing을 가능하게 한다. 로컬 style mixing의 경우 각 $h_t$는 Slerp 전에 마스킹되고 혼합 $h_t$는 원본 feature map에 삽입된다. DiffStyle의 알고리즘은 아래와 같다. 단순성을 위해 알고리즘에서 스타일 보정 및 품질 부스팅을 생략한다.
Experiments
- Checkpoints
- CelebA-HQ: DDPM++
- LSUN-church / LSUN-bedroom: DDPM++
- AFHQv2-Dog: iDDPM
- MetFaces: ADM & P2-weighting
- Hyperparameter
- 이미지 해상도: 256$\times$256
- $t_\textrm{edit} = 400$, $t_\textrm{boost} = 200$
- $\omega = 0.3$, $\gamma = 0.3$
1. Analyses
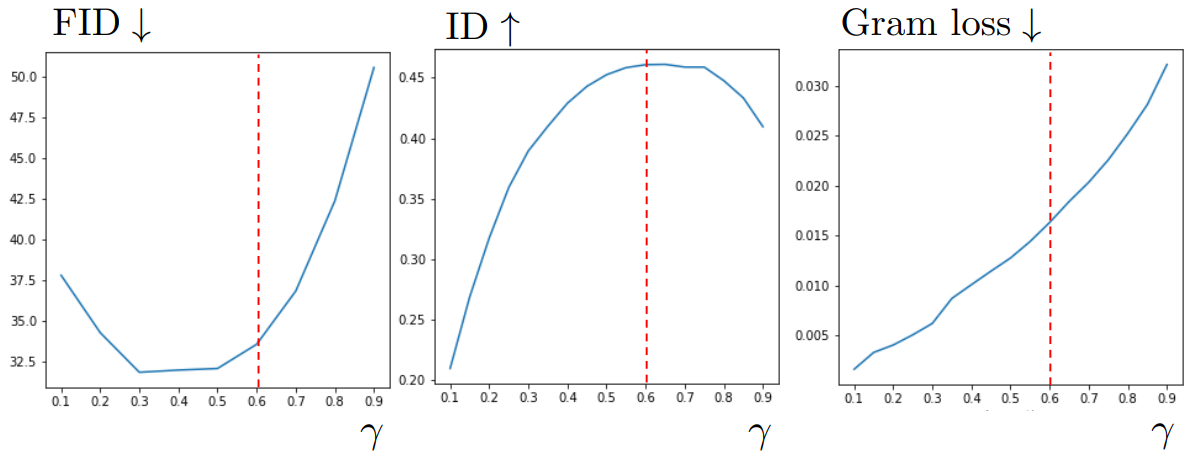
다음은 콘텐츠 주입 비율 $\gamma$에 따른 성능 변화를 나타낸 그래프이다.
다음은 style calibration 유무에 따른 결과를 비교한 것이다.

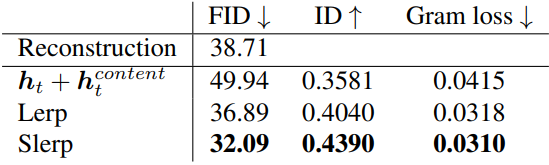
다음은 다양한 구성에 대한 성능을 측정한 표이다.
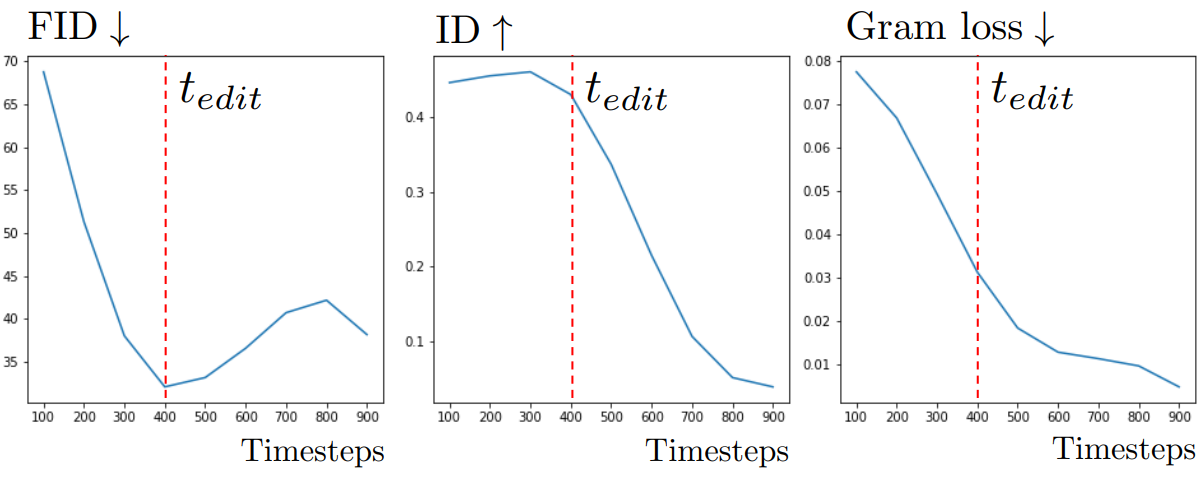
다음은 $t_\textrm{edit}$에 따른 성능 변화를 나타낸 그래프이다.
2. Applications
다음은 다양한 데이터셋에서의 콘텐츠 주입에 대한 결과이다.

다음은 CelebA-HQ에서의 style mixing과 style transfer 결과이다.

3. Comparison with existing methods
다음은 DiffStyle을 DiffuseIT와 비교한 결과이다.

4. DiffStyle on Stable Diffusion
다음은 Stable Diffusion에 DiffStyle을 적용한 결과이다.
