[논문리뷰] DiffFit: Unlocking Transferability of Large Diffusion Models via Simple Parameter-Efficient Fine-Tuning
arXiv 2023. [Paper]
Enze Xie, Lewei Yao, Han Shi, Zhili Liu, Daquan Zhou, Zhaoqiang Liu, Jiawei Li, Zhenguo Li
Huawei Noah’s Ark Lab
13 Apr 2023

Introduction
DDPM은 최근 생성 모델링을 위한 강력한 기술로 부상했으며 이미지 합성, 동영상 생성 및 3D 편집에서 인상적인 결과를 보여주었다. 그러나 현재의 SOTA DDPM은 큰 파라미터 크기와 이미지당 많은 inference step으로 인해 상당한 계산 비용이 발생한다. 예를 들어 DALL·E 2는 4개의 개별 diffusion model로 구성되며 55억개의 파라미터가 필요하다. 실제로 모든 사용자가 필요한 컴퓨팅 및 스토리지 리소스를 감당할 수 있는 것은 아니다. 따라서 특정 task에 효과적으로 적합하도록 사전 학습된 대형 diffusion model을 적응시키는 방법을 모색할 필요성이 있다. 이에 비추어 볼 때 중요한 문제가 발생한다.
사전 학습된 대형 diffusion model을 효율적으로 fine-tuning하는 저비용의 방법을 고안할 수 있는가?
최근 인기 있는 Diffusion Transformer (DiT)를 예로 들면, DiT-XL/2 모델은 DiT에서 가장 큰 모델이며 ImageNet 클래스 조건부 생성 벤치마크에서 SOTA 생성 성능을 달성하였다. 세부적으로 DiT-XL/2는 6.4억개의 파라미터로 구성되며 계산적으로 까다로운 학습 절차를 포함한다. 256$\times$256 이미지에 대한 DiT-XL/2의 학습 프로세스에는 950 V100 GPU day (700만 iteration)가 필요한 반면 512$\times$512 이미지에 대한 학습에는 1733 V100 GPU day (300만 iteration)가 필요하다. 계산 비용이 높기 때문에 대부분의 사용자가 처음부터 DiT를 학습하는 것은 불가능하다. 또한 다양한 하위 데이터셋에서 DiT를 광범위하게 fine-tuning하려면 전체 모델의 여러 복사본을 저장해야 하므로 스토리지 비용이 선형적으로 발생한다.
본 논문에서는 DiT를 기본 모델로 구축하여 대규모 diffusion model을 위한 간단하고 효율적인 fine-tuning 전략인 DiffFit을 제안한다. 자연어 처리의 최근 연구인 BitFit은 사전 학습된 모델의 bias 항만 fine-tuning하면 하위 task에서 충분히 잘 수행됨을 보여주었다. 따라서 본 논문은 이러한 효율적인 fine-tuning 기술을 이미지 생성 task로 확장하고자 한다. 저자들은 BitFit을 직접 적용하는 것으로 시작하여 BitFit을 단순히 사용하는 것이 적응을 위한 좋은 baseline임을 경험적으로 관찰하였다. 그런 다음 학습 가능한 scaling factor $\gamma$를 모델의 특정 레이어에 도입하고, 1.0으로 초기화하고, 데이터셋별로 만들어 feature scaling을 향상시키고 새로운 도메인에 더 잘 적응할 수 있도록 한다. 흥미롭게도 경험적 결과는 모델의 특정 위치에 $\gamma$를 통합하는 것이 더 나은 FID에 도달하는 데 중요하다는 것을 보여준다. 즉, FID는 모델에 포함된 $\gamma$의 개수에 따라 선형적으로 개선되지 않는다.
Methodology
1. Preliminaries
Diffusion Models
(자세한 내용은 DDPM 논문리뷰 참고)
DDPM은 Gaussian noise를 데이터에 점진적으로 추가한 다음 다시 되돌려 생성 모델을 정의한다. 실제 데이터 샘플 $x_0 \sim q_\textrm{data} (x)$가 주어지면 forward process는
\[\begin{equation} q(x_t \vert x_{t-1}) = \mathcal{N} (x_t; \sqrt{1 - \beta_t} x_{t-1}, \beta_t I) \end{equation}\]로서 Markov chain에 의해 제어된다. 여기서 $\beta_t$는 분산이다. Reparameterization trick을 사용하면
\[\begin{equation} x_t = \sqrt{\vphantom{1} \bar{\alpha}_t} x_0 + \sqrt{1 - \bar{\alpha}_t} \epsilon \epsilon \sim \mathcal{N}(0, I), \quad \alpha_t = 1 - \beta_t, \quad \bar{\alpha}_t = \prod_{i=1}^t \alpha_i \end{equation}\]가 된다. 더 큰 timestep $t$의 경우 $\bar{\alpha}_t$가 더 작아지고 샘플의 noise가 더 커진다.
Reverse process에서 DDPM은 신경망
\[\begin{equation} p_\theta (x_{t-1} \vert x_t) = \mathcal{N} (x_{t−1}; \mu_\theta (x_t, t), \sigma_t^2 I) \end{equation}\]을 학습한다. 해당 목적 함수는 다음과 같은 negative log-likelihood의 variational lower bound (VLB)이다.
\[\begin{equation} \mathcal{L} (\theta) = \sum_t D_\textrm{KL} (q(x_{t-1} \vert x_t, x_0) \;\|\; p_\theta (x_{t-1} \vert x_t)) - p_\theta (x_0 \vert x_1) \end{equation}\]여기서 $D_\textrm{KL} (p || q)$는 두 분포 $p$와 $q$의 거리를 측정하는 KL divergence이다. 또한 목적 함수는
\[\begin{equation} \mathcal{L}_\textrm{vlb} = \mathbb{E}_{x_0, \epsilon, t} \bigg[ \frac{\beta_t^2}{2 \alpha_t (1 - \bar{\alpha}_t) \sigma_t^2} \| \epsilon - \epsilon_\theta \|^2 \bigg] \end{equation}\]와 simple loss function
\[\begin{equation} \mathcal{L}_\textrm{simple} = \mathbb{E}_{x_0, \epsilon, t} [ \| \epsilon - \epsilon_\theta \|^2 ] \end{equation}\]로 줄일 수 있다.
본 논문은 iDDPM을 따라 hybrid loss function
\[\begin{equation} \mathcal{L}_\textrm{hybrid} = \mathcal{L}_\textrm{simple} + \lambda \mathcal{L}_\textrm{vlb} \end{equation}\]을 사용한다. 여기서 $\lambda$는 실험에서 0.001로 설정된다.
Diffusion Transformers (DiT)
Transformer 아키텍처는 이미지 인식에서 강력한 것으로 입증되었으며 그 디자인은 이미지 생성을 위해 diffusion model로 옮길 수 있다. DiT는 Transformers로 diffusion model을 설계하는 대표적인 방법이다. DiT는 학습 샘플 $x$가 주어진 두 부분으로 구성된 latent diffusion model (LDM)의 설계를 따른다.
- 인코더 $E$와 디코더 $D$로 구성된 오토인코더. Latent code는 $z = E(x)$이고 재구성된 데이터는 $\hat{x} = D(z)$.
- Latent diffusion transformer. Patchify 연산, 일련의 DiT 블록, Depatchify 연산으로 구성.
각 블록 $B_i$에서 $z_i = B_i(x, t, c)$를 얻을 수 있다. 여기서 $t$와 $c$는 시간 임베딩과 클래스 임베딩이다. 각 블록 $B_i$에는 self-attention과 feed-forward 모듈이 포함되어 있다. Patchify 연산은 latent code $z$를 이미지 토큰 시퀀스로 인코딩하는 데 사용된다. Depatchify 연산은 latent code $z$를 이미지 토큰 시퀀스로부터 디코딩하는 데 사용된다.
2. Parameter-efficient Fine-tuning
DiffFit Design
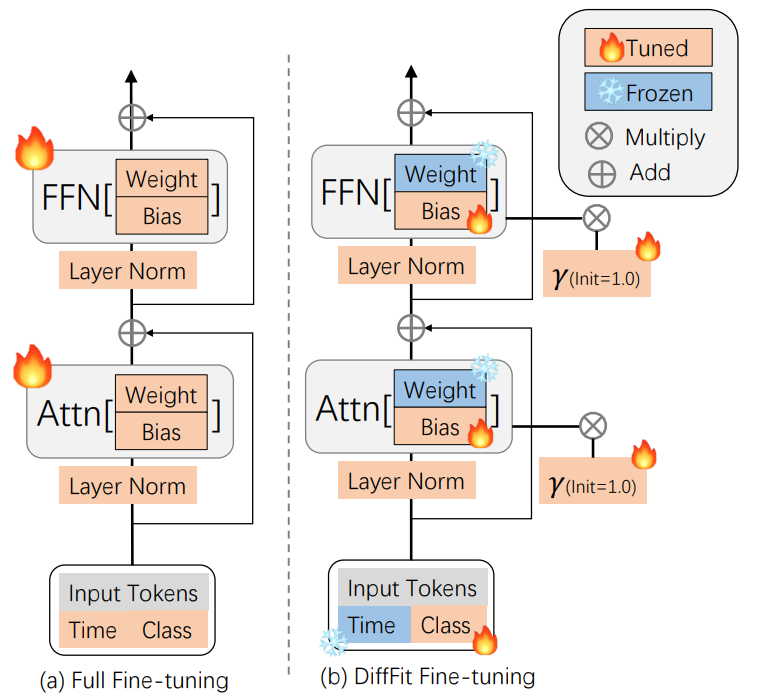
DiffFit은 다른 diffusion model (ex. Stable Diffusion)로 일반화될 수 있다. 위 그림에 설명된 본 논문의 접근 방식은 latent diffusion model에서 대부분의 파라미터를 고정하고 bias 항, normalization, 클래스 조건 모듈만 학습한다. 또한 학습 가능한 scale factor $\gamma$를 diffusion model의 여러 블록에 삽입한다. 여기서 $\gamma$는 1.0으로 초기화되고 각 블록의 해당 layer에 곱해진다. 각 블록은 일반적으로 multihead self-attention, feed-forward networks, layer normalization과 같은 여러 구성 요소를 포함하며 블록은 $N$번 쌓일 수 있다. 자세한 내용은 Algorithm 1과 같다.

Fine-tuning
Fine-tuning 중에 diffusion model 파라미터는 초기에 고정된 후 bias, 클래스 임베딩, normalization, scale factor와 관련된 특정 파라미터만 선택적으로 고정 해제된다. Algorithm 2에 요약된 본 논문의 접근 방식은 사전 학습된 가중치에 대한 중단을 최소화하면서 빠른 fine-tuning을 가능하게 한다. DiT-XL/2는 파라미터의 0.12%만 업데이트하면 되므로 완전한 fine-tuning보다 학습 시간이 약 2배 빨라진다. 본 논문의 접근 방식은 사전 학습된 모델의 지식을 강화하고 특정 task에 적응할 수 있도록 하면서 학습한 지식을 잊지 않도록 한다.

Inference and Storage
$K$개의 데이터셋에서 fine-tuning한 후 원본 모델의 전체 파라미터와 데이터셋별 학습 가능한 파라미터의 복사본을 하나씩만 저장하면 된다. 일반적으로 학습 가능한 파라미터들은 총 100만 개 미만이다. Diffusion model에 대해 이러한 가중치를 결합하면 클래스 조건부 이미지 생성을 위해 여러 도메인에 적응할 수 있다.
Experiments
- Implementation Details
- Base model: ImageNet 256$\times$256에서 사전 학습된 DiT (FID: 2.27)
- DIT repository가 학습 코드를 제공하지 않아 재구현 후 학습 진행
- learning rate: $10^{-4}$
- classifier-free guidance: 평가에는 1.5, 시각화에는 4.0 사용
1. Transfer to Downstream Datasets
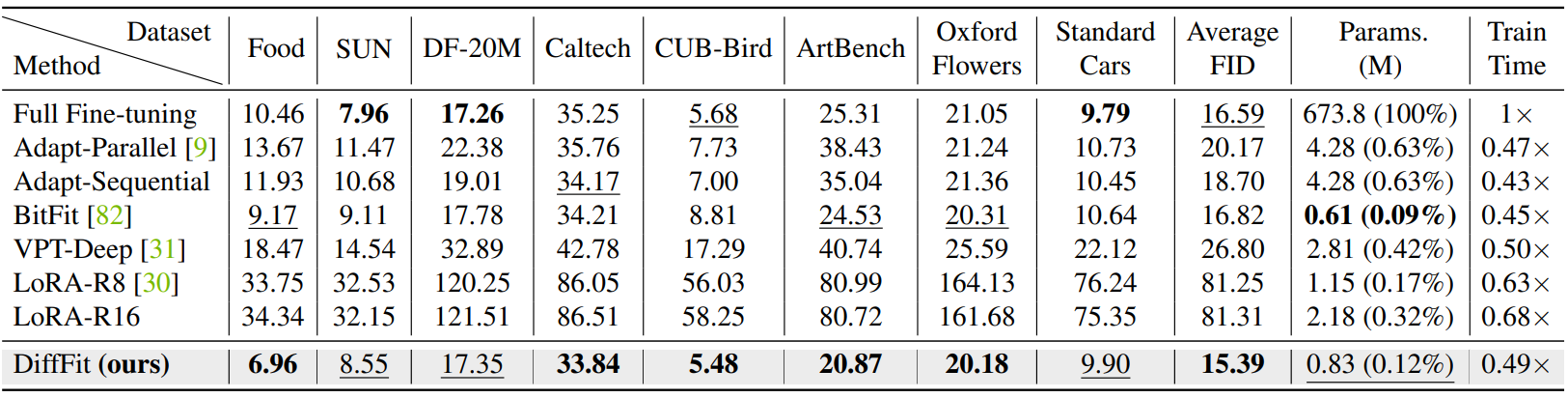
다음은 하위 데이터셋에 대한 FID 성능을 다른 fine-tuning 방법들과 비교한 표이다.
2. From Low Resolution to High Resolution
Positional Encoding Trick
DiT는 정적 sinusoidal 2D 위치 인코딩을 사용한다. 사전 학습된 모델에서 인코딩된 위치 정보를 더 잘 활용하기 위해 위치 인코딩 공식의 각 픽셀 좌표 $(i, j)$를 절반 값 $(i/2, j/2)$으로 대체하여 구현되며 간단하고 추가 비용이 없다. 이를 이용해 512$\times$512 해상도의 위치 인코딩을 256$\times$256 해상도의 위치 인코딩과 정렬시킨다.
Results
다음은 ImageNet 512$\times$512에서의 클래스 조건부 이미지 생성 결과이다. ($+950^\dagger$)은 DiT-XL/2의 사전 학습에 걸린 시간이다.
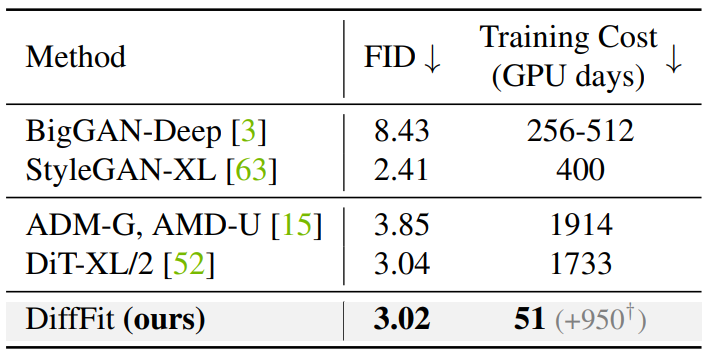
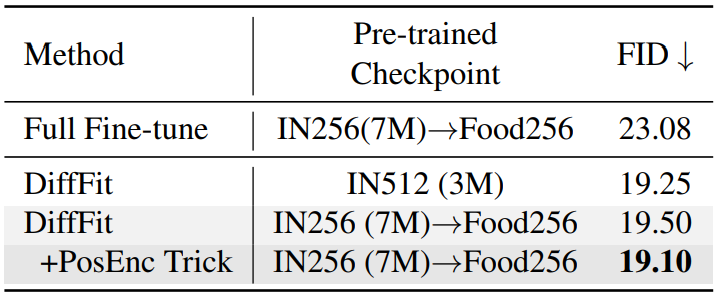
다음은 DiffFit을 positional encoding trick과 함께 사용하여 DiT-XL/2-256의 checkpoint에서 DiT-XL/2-512를 fine-tuning한 결과이다.

다음은 Food101 512$\times$512에서의 클래스 조건부 이미지 생성 결과이다. IN은 ImageNet을 의미한다.
3. Fine-tuning Convergence Analysis
다음은 4가지 하위 데이터셋에서 5가지 방법의 FID를 비교한 그래프이다.

4. Ablation studies
저자들은 4가지 ablation study를 진행하였다.
- 깊은 layer에서 얕은 레이어로 점진적으로 $\gamma$를 추가
- 얕은 layer에서 깊은 레이어로 점진적으로 $\gamma$를 추가
- 다양한 모듈에서의 $\gamma$의 영향
- Learning rate
다음은 ablation study 결과이다. 최고의 세팅은 회색으로 표시되었다. LR Ratio는 사전 학습 시 사용된 learning rate에 대한 비율이다.