[논문리뷰] Differential Diffusion: Giving Each Pixel Its Strength
arXiv 2023. [Paper] [Page] [Github]
Eran Levin, Ohad Fried
Tel Aviv University | Reichman University
1 Jun 2023

Introduction
이미지를 편집하려는 경우 Photoshop을 통한 수동 편집과 같은 기존 접근 방식 외에도 최신 AI 도구를 사용할 수 있다. 예를 들어 텍스트 지침을 통해 이미지를 편집할 수 있다. 최근 몇 년 동안 개발된 가장 성공적인 이미지 generator는 diffusion process를 사용하며, 사진에 적용할 변경량을 구성할 수 있다. 그러나 조각(그림의 특정 영역)을 편집하려면 다른 방법이 필요하다. Blended Diffusion과 같은 연구에서는 binary로 편집할 그림의 조각을 선택할 수 있다. 그러나 기껏해야 이분법적인 선택이다. 일반적으로 그림을 편집할 때 강도(strength)라고 하는 한 가지 변경 사항만 지정할 수 있다. 이미지의 조각은 같은 강도로 변경되거나 전혀 변경되지 않으며, 이것은 제한적이다.
때때로 편집하는 사람은 이미지의 서로 다른 영역을 서로 다른 양만큼 변경하려고 한다. 또한 때로는 인접한 조각 간에 연속적인 전환을 원할 수도 있다. 이것은 때때로 시각적으로 더 유리하고 사실적이다.
본 논문은 사용자가 이미지의 각 픽셀의 편집 강도를 결정하여 이미지의 어느 부분을 그대로 유지할지, 어느 부분을 얼마만큼 변경할지 제어할 수 있는 프롬프트 기반 이미지 편집을 위한 새로운 기술을 제시한다. 이전 방법들과 달리 사용자가 binary가 아닌 방식으로 변경량을 선택할 수 있으므로 더 큰 유연성과 더 세밀한 이미지 편집이 가능하다.
Method
이미지, 각 픽셀의 편집 강도를 나타내는 단일 채널 변경 맵 (change map), 편집을 안내하는 텍스트 프롬프트가 주어지면 이미지를 편집하는 것을 목표로 한다. 생성된 결과가 강도 제약 조건을 충족하고 사실적이며 프롬프트를 준수하기를 원한다.
1. Overview
Diffusion model은 일반적으로 임의의 Gaussian noise로 인해 손상된 이미지의 noise를 제거하도록 점진적으로 학습된다. 일반적으로 이미지 간 변환 프로세스 (inference process)는 Gaussian noise가 추가된 이미지로 시작한 다음 반복 프로세스에서 noise가 점차 제거된다. 이 inference process는 일련의 이미지를 생성하며, 각 이미지는 이전 이미지의 denoising process (inference chain)의 결과이다.
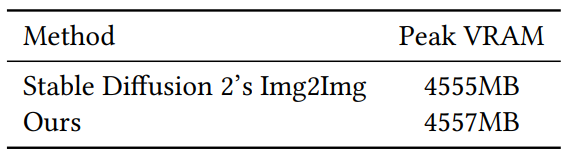
프롬프트는 생성된 세그먼트의 내용을 설명하는 텍스트이다. 강도는 이미지의 변화량을 안내하는 파라미터이다. 일반적으로 전체 이미지에 대한 단일 강도 파라미터가 있다. 본 논문에서는 change map 또는 단순히 “map”을 통해 이미지의 각 조각에 대해 서로 다른 강도를 허용한다. 이는 원본 이미지의 높이와 너비가 같고, 0과 1 사이의 값으로 각 픽셀에 적용할 강도를 나타내는 텐서이다. 완전한 변화를 흰색(1)이 아닌 검은색(0)으로 표시한다.
Latent Diffusion Model에서 latent 인코더는 이미지를 더 작은 latent space로 압축하는 신경망이며 diffusion process를 적용한다. 프로세스가 끝나면 latent 디코더가 latent 출력을 이미지로 압축 해제한다.
본 논문에서는 change map을 통해 각 이미지 조각에 적용되는 변경량을 제어하는 기능을 추가하는 image-to-image diffusion model의 향상된 버전인 Differential Diffusion을 제시한다 (Algorithm 1). 이 방법은 inference process만 변경한다.

2. Observations
저자들은 알고리즘을 설계하기 위해 세 가지 주요 observation을 만들었다.
- Timestep의 두 가지 일련의 인덱스가 주어지면 동일한 파라미터와 동일한 강도 파라미터에 의해 생성된 두 inference process를 $A$와 $B$하 하자. 일반성을 잃지 않고 $A$의 inference process가 $B$보다 더 강하다고 하자. 그러면 $B \subseteq A$이고 $\exists i \ge 0 (\forall j \ge 0 (B[j] = A[i+j]))$이다. 이는 $B$가 $A$의 잘린 시퀀스임을 의미한다.
- Inference process를 중단하지 않고 chain의 중간 step $t$에 latent space에 인코딩된 해당하는 noisy한 조각을 삽입할 수 있다. 이것을 injection이라고 부른다.
- Stable Diffusion의 latent 인코더는 일반적으로 픽셀을 동일한 상대 위치로 인코딩한다. 즉, 그림에서 아주 작은 모양이 아닌 경우 상대 위치를 계산하는 것만으로 latent 인코더의 위치를 추정할 수 있다. 이 속성을 locality라고 부른다.
3. Change Map Down-Sampling
Map은 diffusion process가 픽셀 space가 아닌 latent space에서 수행되므로 높이와 너비가 latent space 인코딩의 크기와 일치하도록 다운 샘플링된다 (동일한 map이 모든 채널에 적용됨). Locality로 인해 다운샘플링된 map은 latent 텐서의 latent 픽셀 위치와 일치한다.
4. Fragment Injection
Latent space에서 조각을 대체하는 프로세스인 injection이라는 새로운 연산을 정의한다. Noise가 있는 latent space에서 조각을 교체할 때 현재 timestep에 따라 인코딩되고 noise가 있는 세그먼트를 주입해야 한다.
Gradual Injection
사용자가 지정한 change map과 일치하는 timestep과 noise에 조각을 주입한다. 강도 값이 가장 작은 조각이 마지막에 추가되며 noise도 가장 적다. 이를 통해 점진적 이미지 생성 프로세스를 활용한다.
- 최종 injection이 늦을수록 입력에 대한 출력에서 이 조각의 유사성이 더 커진다. 조각이 더 적은 iteration으로 변경되기 때문에 더 적은 변경이 이 조각에 적용된다.
- 주입된 조각에 추가되는 noise의 양은 이 조각에 적용될 step 수에 비례한다. 조각이 참여하는 step이 많을수록 더 많은 noise가 추가된다. 이는 모든 조각에 동시에 noise가 발생하므로 다르게 noise가 발생하지 않아야 하는 일반적인 inference process와 다른 주요 변경 사항이다.
Future Hinting

지정된 강도에 따라 각 조각을 한 번만 주입하면 충분하다고 가정하고 싶을 것이다. 대부분의 image-to-image translation 절차에서 모든 조각이 첫 번째 timestep에 삽입되므로 이는 합리적으로 보일 수 있다. 그러나 새로운 inference process 전반에 걸쳐 일부 조각을 반복적으로 다시 주입한다. 임의의 timestep $k$에서 $k$에 해당하는 조각과 미래 timestep ($< k$)에 해당하는 조각을 주입한다. 모두 $k$의 양에 의해 noise가 발생한다. 따라서 강도가 가장 낮은 조각의 경우 프로세스는 noisy한 조각을 여러 번 주입한다 (위 그림 참조). 이 동작을 future hinting이라고 하며, 몇 가지 목표를 제공한다.
- Diffusion model에 다가오는 시각적 데이터 중 일부에 대한 사전 지식을 제공하여 보다 복잡한 객체를 계획할 수 있도록 한다. 모델이 전체 그림의 내용에 따라 결정을 내리도록 한다.
- 일반적으로 diffusion model은 대부분 구멍이 없는 사진에 대해 학습된다. 따라서 중간 diffusion step에서 구멍 뚫린 픽셀이 있는 diffusion process에 덜 견고할 것으로 예상된다. Future hinting은 그러한 구멍을 적절한 데이터로 채우는 자연스러운 방법이다.
Future hinting의 유무에 따른 결과는 아래와 같다.

5. Technical Details
- 모델: Stable Diffusion 2.1의 512-base-ema.ckpt
- 프롬프트: 표준 Stable Diffusion 프롬프트 사용
- 마스크: 어떤 마스크도 사용 가능 (실험에서는 Segment-anything, MiDaS, 수동으로 그린 mask 사용)
- 기타 설정: 100 inference step 사용
Results
다음은 강도에 따른 편집 효과를 나타낸 것이다.

다음은 각 timestep에 injection을 사용한 Differential Diffusion의 중간 step들이다.

다음은 다양한 출력 예시들이다.

다음은 사실적인 사진에 예술적인 요소를 혼합한 예시이다. (프롬프트: “a futuristic city”)

1. Comparisons
다음은 Differential Diffusion을 Blend Latent Diffusion과 Stable Diffusion 2.1과 비교한 것이다.

2. Evaluation
Trend Reconstruction
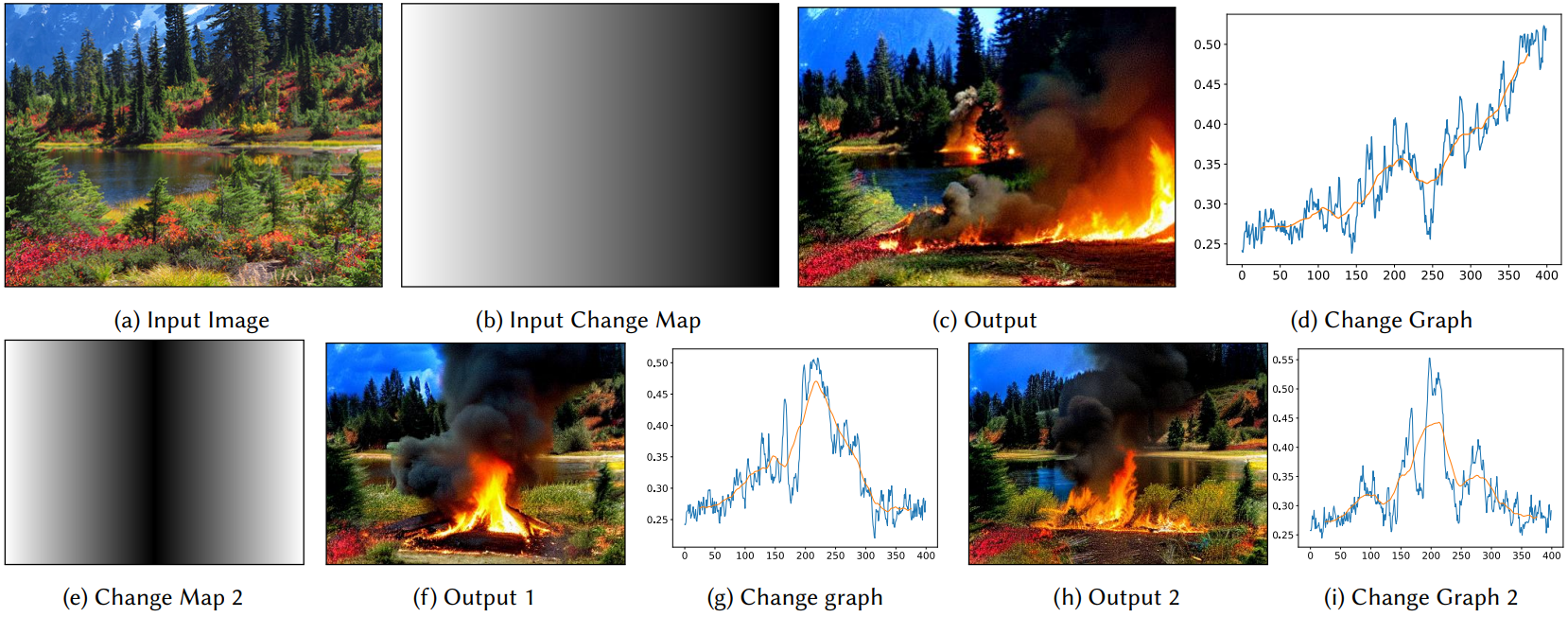
Change map에 대한 결과의 준수 여부를 평가한다. 예를 들어 1에서 0으로 점진적으로 변화하는 맵은 거의 변하지 않는 조각에서 입력과 완전히 다른 조각으로 점진적으로 변화하는 이미지를 생성해야 한다. 이미지 콘텐츠와 이미지의 y축 사이에는 고유한 관계가 있다. 실험에 따르면 모든 기술은 특정 높이에서의 편집을 선호하는 경향이 있다. 따라서 이를 고려하여 측정해야 하며 타겟 change map에 대한 픽셀 차이를 단순히 측정할 수 없다.
저자들은 trend reconstruction 테스트를 수행하였다. 즉, 수평 기울기 맵을 사용하고 열을 따라 평균이 선형으로 변경되는지 여부를 측정하였다. 직관적으로 기울기 맵이 사진의 변화에 의해 모방되는 것에 주로 관심을 가진다. 열을 따라 평균화하면 측정 noise도 감소해야 한다. 아래 그림은 결과가 기울기 맵을 따른다는 것을 보여준다.
Reliability score
저자들은 이 속성을 수치화하기 위해 다음 사항을 고려하여 수치 측정을 설정한다.
- 모든 방법에 대해 단일 이미지에 대한 결과에는 상당한 noise가 포함되어 있다. 이는 diffusion process가 본질적으로 확률론적이기 때문이다.
- 모든 방법은 그림 경계 근처의 조각에서 더 많이 변경하는 쪽으로 편향되어 있다.
- 전체 그림을 변경하더라도 (모든 픽셀에 대해 변경 맵을 0으로 설정) 일부 조각은 순전히 우연의 일치로 인해 입력과 유사한 출력으로 변경된다.
- Change map은 픽셀 차이 측정과 다른 scale과 bias를 갖는다 (즉, 추세는 유사해야 하지만 측정 단위는 동일하지 않음).
따라서 저자들은 다음 메트릭을 제안하였다. 데이터셋 $\mathcal{D}$와 높이 $h$의 단일 change map $\mu$, 편집할 그림 $d$, 편집 기술 $S$가 주어지면 편집된 이미지 (3D 텐서 - 높이, 너비, 채널)를 리턴한다. 각 인덱스 $i$에 대해 reconstruct된 trend $\tau_{\mathcal{D}, \mu, S}$는 다음과 같다.
\[\begin{equation} \tau_{\mathcal{D}, \mu, S} [i] = \sum_{d \in \mathcal{D}} \frac{\| S (d, \mu) [:, i, :] - d [:, i, :] \|_2}{ | \mathcal{D} | h} \end{equation}\]차원이 $h$, $w$인 0 행렬을 $\xi = 0_{h, w}$라고 하면 $xi$는 모든 것을 변경하는 change map이다. 정규화된 trend는 다음과 같이 정의된다.
\[\begin{equation} \hat{\tau}_{\mathcal{D}, \mu, S} = \tau_{\mathcal{D}, \mu, S} - \tau_{\mathcal{D}, \xi, S} \end{equation}\]$G$를 $\forall i \forall j ( G[i, j] = 1 - j / h )$를 만족하는 change map이라고 하자. 편집 방법 S가 주어지면 이 방법의 신뢰도 점수는
\[\begin{equation} R_{\mathcal{D}, S} = \rho (\hat{\tau}_{\mathcal{D}, G, S}, I) \end{equation}\]이다. 여기서 $I$는 열의 인덱스로 구성된 벡터 $[0, \cdots, w-1]$이며, $\rho$는 Pearson 상관 계수이다. Pearson 상관 계수는 두 개의 변수가 있는 위치 및 양의 스케일에 대해 불변이다.
다음은 reliability score $R$을 나타낸 표이다.

다음은 reliability score $R$을 비교한 그래프이다.
3. Memory Consumption
다음은 VRAM 최고치를 나타낸 표이다.