[논문리뷰] End-to-End Object Detection with Transformers (DETR)
ECCV 2020. [Paper] [Github]
Nicolas Carion, Francisco Massa, Gabriel Synnaeve, Nicolas Usunier, Alexander Kirillov, Sergey Zagoruyko
Facebook AI
26 May 2020
Introduction
Object detection의 목표는 관심 있는 각 개체에 대한 boundary box와 카테고리 레이블 집합을 예측하는 것이다. 최신 detector는 대규모 proposal, 앵커, window 중심 세트에서 회귀 및 분류 문제를 정의하여 이 세트 예측 task를 간접적인 방식으로 처리한다. 이들의 성능은 거의 중복된 예측을 축소하는 후처리 단계, 앵커 세트의 디자인, 타겟 박스를 앵커에 할당하는 휴리스틱에 의해 크게 영향을 받는다.
본 논문은 이러한 파이프라인을 단순화하기 위해 task를 우회하는 직접적인 집합 예측 접근 방식을 제안하였다. 이 end-to-end 철학은 기계 번역이나 음성 인식과 같은 복잡한 구조적 예측 task에서 상당한 발전을 가져왔지만 object detection에서는 아직 그렇지 않다. 이전 시도들은 다른 형태의 사전 지식을 추가하거나 도전적인 벤치마크에 대한 강력한 baseline보다 성능이 떨어진다. 이 논문은 이러한 격차를 해소하는 것을 목표로 한다.
Object detection을 직접적인 집합 예측 문제로 간주하여 학습 파이프라인을 간소화한다. 시퀀스 예측에 널리 사용되는 아키텍처인 transformer를 기반으로 하는 인코더-디코더 아키텍처를 채택한다. 시퀀스의 요소 간의 모든 쌍별 상호 작용을 명시적으로 모델링하는 transformer의 self-attention 메커니즘은 이러한 아키텍처를 특히 중복 예측 제거와 같은 집합 예측의 특정 제약 조건에 적합하게 만든다.

DEtection TRansformer (DETR)는 한 번에 모든 개체를 예측하고 예측 개체와 ground-truth 개체 사이에 이분 매칭을 수행하는 set loss function으로 end-to-end로 학습된다. DETR은 공간 앵커 또는 non-maximal suppression (NMS)과 같은 사전 지식을 인코딩하는 여러 구성 요소를 삭제하여 파이프라인을 단순화한다. 대부분의 기존 detection 방법과 달리 DETR은 사용자 정의된 레이어가 필요하지 않으므로 표준 CNN과 transformer 클래스를 포함하는 모든 프레임워크에서 쉽게 재현할 수 있다.
직접적인 집합 예측에 대한 대부분의 이전 연구들과 비교하여 DETR의 주요 특징은 이분 매칭 loss와 병렬 디코딩이 있는 transformer (non-autoregressive)의 결합이다. 대조적으로, 이전 연구들은 RNN을 사용한 autoregressive 디코딩에 중점을 두었다. 매칭 loss function은 ground-truth 개체에 예측을 고유하게 할당하고 예측 개체의 순열에 불변하므로 병렬로 출력할 수 있다.
DETR에 대한 학습 설정은 여러 면에서 표준 object detector와 다르다. DETR은 매우 긴 학습 schedule이 필요하며 transformer의 보조 디코딩 loss로 인한 이점이 있다.
The DETR model
탐지에서 직접적인 집합 예측을 위해서는 두 가지 요소가 필수적이다.
- 예측 박스와 ground-truth 박스 간에 고유한 일치를 강제하는 집합 예측 loss
- 개체 집합을 예측하고 해당 관계를 모델링하는 아키텍처
1. Object detection set prediction loss
DETR은 디코더를 통한 단일 pass에서 고정된 크기의 $N$개의 예측 집합을 추론한다. 여기서 $N$은 이미지의 일반적인 개체 수보다 훨씬 더 크게 설정된다. 학습의 주요 어려움 중 하나는 ground truth와 관련하여 예측된 개체 (클래스, 위치, 크기)에 점수를 매기는 것이다. Loss는 예측 개체와 ground-truth 개체 간에 최적의 이분 매칭을 생성한 다음 개체별 (boundary box) loss를 최적화한다.
Ground-truth 개체 집합을 $y$로 표시하고 $N$개의 예측 집합을 \(\hat{y} = \{\hat{y_i}\}_{i=1}^N\)로 표시한다. $N$이 이미지의 개체 수보다 크다고 가정하면 $y$도 $\emptyset$(개체 없음)로 채워진 크기 $N$의 집합으로 간주한다. 이 두 집합 사이의 이분 매칭을 찾기 위해 가장 낮은 비용으로 $N$개의 요소의 순열 \(\sigma \in \mathfrak{S}_N\)을 검색한다.
\[\begin{equation} \hat{\sigma} = \underset{\sigma \in \mathfrak{S}_N}{\arg \min} \sum_i^N \mathcal{L}_\textrm{match} (y_i, \hat{y}_{\sigma (i)}) \end{equation}\]여기서 \(\mathcal{L}_\textrm{match} (y_i, \hat{y}_{\sigma (i)})\)는 ground truth $y_i$와 index $\sigma (i)$에 대한 예측 사이의 쌍별 matching cost이다. 이 최적 할당은 Hungarian 알고리즘을 사용하여 효율적으로 계산된다.
Matching cost는 클래스 예측과 예측 박스와 ground-truth 박스의 유사성을 모두 고려한다. Ground-truth 집합의 각 요소 $i$는 $y_i = (c_i, b_i)$로 볼 수 있다. 여기서 $c_i$는 타겟 클래스 레이블 ($\emptyset$일 수 있음)이고 $b_i \in [0, 1]^4$는 ground-turth box의 중심 좌표와 이미지 크기에 상대적인 높이 및 너비를 정의하는 벡터이다. 인덱스 $\sigma (i)$를 사용한 예측의 경우 클래스 $c_i$의 확률을 \(\hat{p}_{\sigma (i)} (c_i)\)로 정의하고 예측된 박스를 \(\hat{b}_{\sigma (i)}\)로 정의한다. 이러한 표기법으로 다음과 같이 정의한다.
\[\begin{equation} \mathcal{L}_\textrm{match} (y_i, \hat{y}_{\sigma (i)}) = - \textbf{1}_{\{c_i \ne \emptyset\}} \hat{p}_{\sigma (i)} (c_i) + \textbf{1}_{\{c_i \ne \emptyset\}} \mathcal{L}_\textrm{box} (b_i, \hat{b}_{\sigma (i)}) \end{equation}\]매칭을 찾는 이 절차는 proposal 또는 앵커를 최신 detector의 ground-truth 개체에 일치시키는 데 사용되는 휴리스틱 할당 규칙과 동일한 역할을 한다. 주요 차이점은 중복 없이 직접적인 집합 예측을 위해 일대일 매칭을 찾아야 한다는 것이다.
두 번째 단계는 이전 단계에서 매칭된 모든 쌍에 대한 Hungarian loss인 loss function을 계산하는 것이다. 일반적인 object detector의 loss와 유사하게 loss를 정의한다. 즉, 클래스 예측에 대한 log-likelihood와 나중에 정의된 box loss의 선형 결합이다.
\[\begin{equation} \mathcal{L}_\textrm{Hungarian} (y, \hat{y}) = \sum_{i=1}^N [-\log \hat{p}_{\hat{\sigma} (u)} (c_i) + \textbf{1}_{\{c_i \ne \emptyset\}} \mathcal{L}_\textrm{box} (b_i, \hat{b}_{\hat{\sigma} (i)})] \end{equation}\]여기서 $\hat{\sigma}$는 첫 번째 단계에서 계산된 최적 할당이다. 실제로, $c_i = \emptyset$일 때 로그 확률 항의 가중치를 10배 낮춰 클래스 불균형을 해결한다. 이는 Faster R-CNN 학습 절차가 서브샘플링을 통해 긍정적/부정적 proposal의 균형을 맞추는 방법과 유사하다. 개체와 $\emptyset$ 사이의 matching cost는 예측에 의존하지 않는다. 즉, 이 경우 cost는 일정하다. Matching cost에서 로그 확률 대신 확률 \(\hat{p}_{\hat{\sigma} (i)} (c_i)\)를 사용한다. 이는 클래스 예측 항을 \(\mathcal{L}_\textrm{box} (\cdot, \cdot)\)에 상응하게 만들고, 더 나은 경험적 성능을 얻었다고 한다.
Bounding box loss
Matching cost와 Hungarian loss의 두 번째 부분은 boundary box에 점수를 매기는 \(\mathcal{L}_\textrm{box} (\cdot, \cdot)\)이다. 일부 초기 추측과 관련하여 박스 예측을 $\Delta$로 수행하는 많은 detector와 달리 박스 예측을 직접 수행한다. 이러한 접근 방식은 구현을 단순화하지만 loss의 상대적 크기 조정에 문제가 있다. 가장 일반적으로 사용되는 $\ell_1$ loss는 상대적 오차가 비슷하더라도 작은 박스와 큰 박스에 대해 서로 다른 스케일을 갖는다. 이 문제를 완화하기 위해 스케일 불변인 $\ell_1$ loss와 일반화된 IoU loss $$\mathcal{L}_\textrm{iou} (\cdot, \cdot)$의 선형 결합을 사용한다. 전반적으로 box loss는 다음과 같이 정의된다.
\[\begin{equation} \mathcal{L}_\textrm{box} (b_i, \hat{b}_{\sigma (i)}) = \lambda_\textrm{iou} \mathcal{L}_\textrm{iou} (b_i, \hat{b}_{\sigma (i)}) + \lambda_\textrm{L1} \| b_i - \hat{b}_{\sigma (i)} \|_1 \end{equation}\]여기서 \(\lambda_\textrm{iou}, \lambda_\textrm{L1} \in \mathbb{R}\)은 hyperparameter이다. 이 두 가지 loss는 batch 내의 개체 수로 정규화된다.
2. DETR architecture
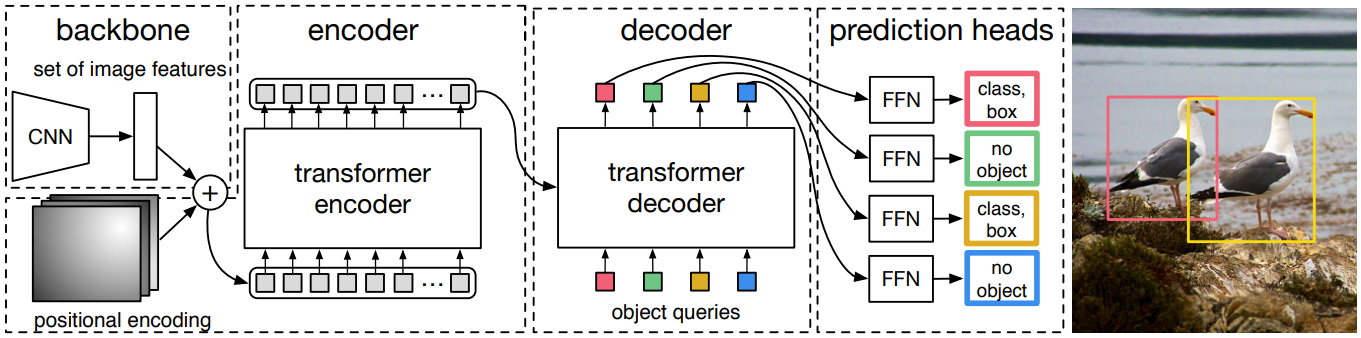
전체 DETR 아키텍처는 놀라울 정도로 단순하며 위 그림에 묘사되어 있다. 여기에는 세 가지 주요 구성 요소가 포함되어 있다.
- 컴팩트한 feature 표현을 추출하기 위한 CNN backbone
- 인코더-디코더 transformer
- 최종 예측을 만드는 간단한 피드포워드 네트워크 (FFN)
Backbone
초기 이미지 \(x_\textrm{img} \in \mathbb{R}^{3 \times H_0 \times W_0}\)에서 시작하여 전통적인 CNN backbone은 저해상도 activation map $f \in \mathbb{R}^{C \times H \times W}$를 생성한다. 일반적으로 $C = 2048$, $H = H_0 / 32$, $W = W_0 / 32$를 사용한다.
Transformer encoder
첫째, 1$\times$1 convolution은 높은 레벨의 activation map $f$의 채널 차원을 $C$에서 더 작은 차원 $d$로 줄여 새로운 feature map $z_0 \in \mathbb{R}^{d \times H \times W}$을 생성한다. 인코더는 시퀀스를 입력으로 예상하므로 $z_0$의 공간 차원을 1차원으로 축소하여 $d \times HW$ feature map을 생성한다. 각 인코더 레이어에는 표준 아키텍처가 있으며 multi-head self-attention 모듈과 피드포워드 네트워크(FFN)로 구성된다. Transformer 아키텍처는 순열 불변이므로 각 attention 레이어의 입력에 추가되는 고정 위치 인코딩으로 이를 보완한다.
Transformer decoder
디코더는 transformer의 표준 아키텍처를 따르며 multi-head self-attention 메커니즘과 인코더-디코더 attention 메커니즘을 사용하여 크기 $d$의 $N$개의 임베딩을 변환한다. DETR은 각 디코더 레이어에서 $N$개의 개체를 병렬로 디코딩하는 반면 원래 transformer는 한 번에 한 요소씩 출력 시퀀스를 예측하는 autoregressive model을 사용한다. 디코더도 순열 불변이므로 다른 결과를 생성하려면 $N$개의 입력 임베딩이 달라야 한다. 이러한 입력 임베딩은 개체 쿼리라고 하는 학습된 위치 인코딩이며 인코더와 유사하게 각 attention 레이어의 입력에 추가한다. $N$개의 개체 쿼리는 디코더에 의해 출력 임베딩으로 변환된다. 그런 다음 피드포워드 네트워크에 의해 박스 좌표와 클래스 레이블로 독립적으로 디코딩되어 $N$개의 최종 예측이 생성된다. 이러한 임베딩에 대해 모델은 self-attention과 인코더-디코더 attention을 사용하여 전체 이미지를 컨텍스트로 사용하면서 쌍별 관계를 사용하여 모든 개체에 대해 글로벌하게 추론한다.
Prediction feed-forward networks (FFNs)
최종 예측은 ReLU 함수를 포함하는 hidden 차원이 $d$인 3-layer MLP와 linear projection layer로 계산된다. FFN은 입력 이미지에 대한 정규화된 중심 좌표, 박스의 높이 및 너비를 예측하고 linear layer는 softmax 함수를 사용하여 클래스 레이블을 예측한다. 고정된 크기의 $N$개의 boundary box 집합을 예측하므로 $N$은 일반적으로 이미지에서 관심 대상의 실제 수보다 훨씬 크다. 추가 특수 클래스 레이블 $\emptyset$은 슬롯 내에서 감지된 물체가 없음을 나타내는 데 사용된다. 이 클래스는 표준 object detection 방식의 “배경” 클래스와 유사한 역할을 한다.
Auxiliary decoding losses
학습 중에 디코더에서 보조 loss를 사용하는 것이 도움이 된다. 특히 모델이 각 클래스의 정확한 개체 수를 출력하는 데 도움이 된다. 각 디코더 레이어 뒤에 예측 FFN과 Hungarian loss를 추가한다. 모든 예측 FFN은 파라미터를 공유한다. 추가로 공유된 layer-norm을 사용하여 다른 디코더 레이어의 예측 FFN에 대한 입력을 정규화한다.
Experiments
- 데이터셋: COCO 2017 detection and panoptic segmentation dataset
- 구현 디테일
- optimizer: AdamW
- learning rate: transformer는 $10^{-4}$, backbone은 $10^{-5}$
- weight decay: $10^{-4}$
- transformer: Xavier init으로 가중치 초기화
- backbone: ImageNet으로 사전 학습된 ResNet
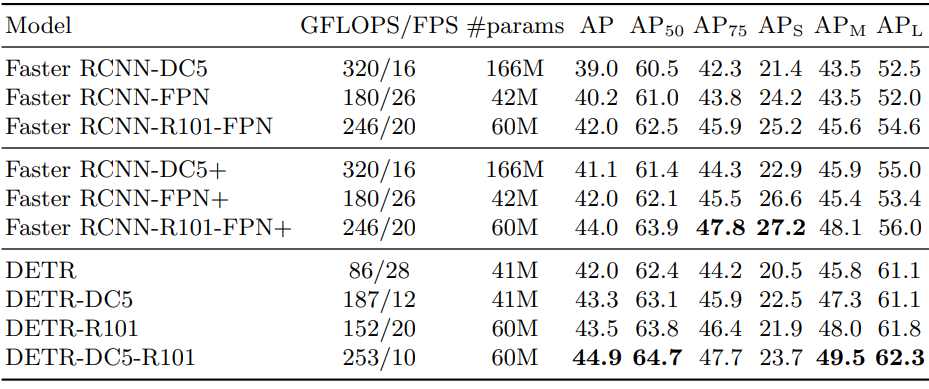
1. Comparison with Faster R-CNN
다음은 COCO validation set에서 Faster R-CNN과 비교한 표이다.
2. Ablations
다음은 인코더 크기에 대한 영향을 나타낸 표이다.

다음은 레퍼런스 포인트들에 대한 인코더 self-attention을 나타낸 것이다.

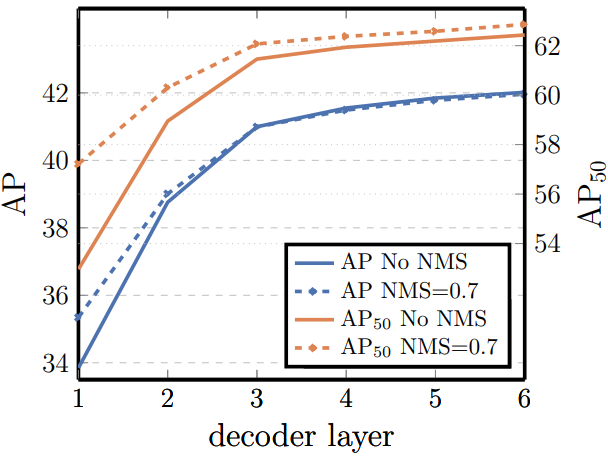
다음은 각 디코더 레이어 이후의 성능 변화를 나타낸 그래프이다.
다음은 모든 예측된 개체에 대하여 디코더 attention을 시각화한 것이다.

다음은 다양한 위치 인코딩에 대한 성능을 나타낸 표이다.
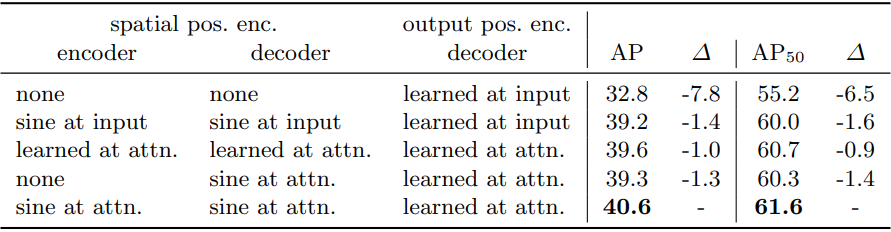
다음은 loss 구성 요소에 대한 영향을 나타낸 표이다.

3. Analysis
다음은 COCO 2017 val set에서 모든 이미지에 대한 모든 박스 예측을 시각화 한 것으로, 총 $N = 100$개의 예측 슬롯 중 20개만 시각화한 것이다.

다음은 드문 클래스에 대한 out of distribution 일반화를 나타낸 것이다.

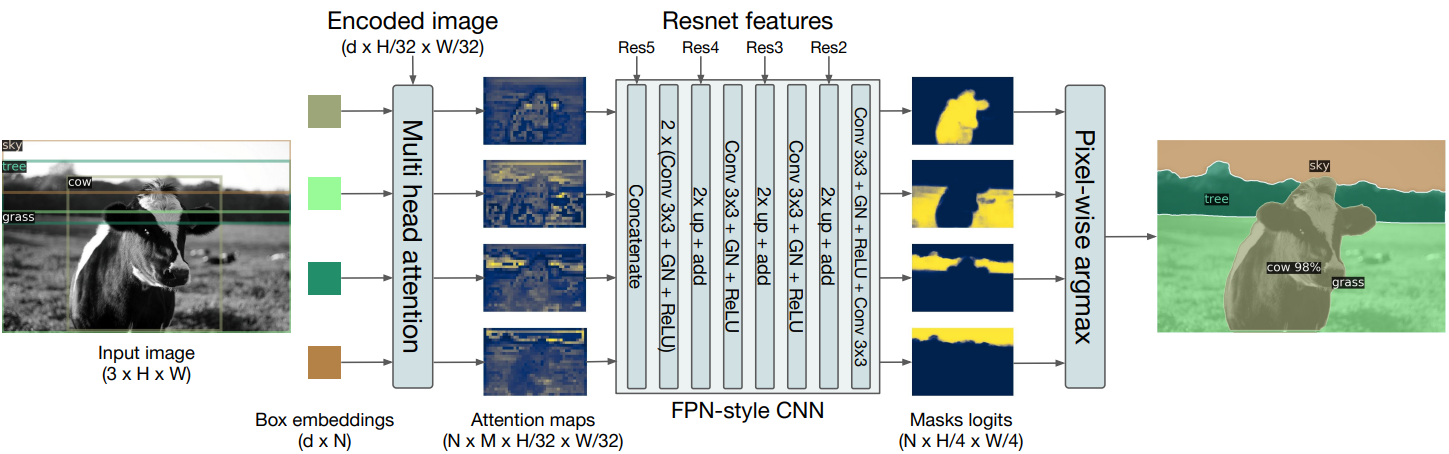
4. DETR for panoptic segmentation
다음은 panoptic head을 설명한 그림이다.
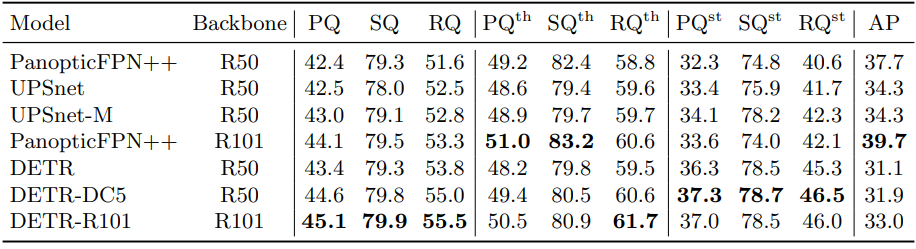
다음은 COCO val dataset에서 panoptic segmentation의 SOTA 방법들과 정량적으로 비교한 표이다.
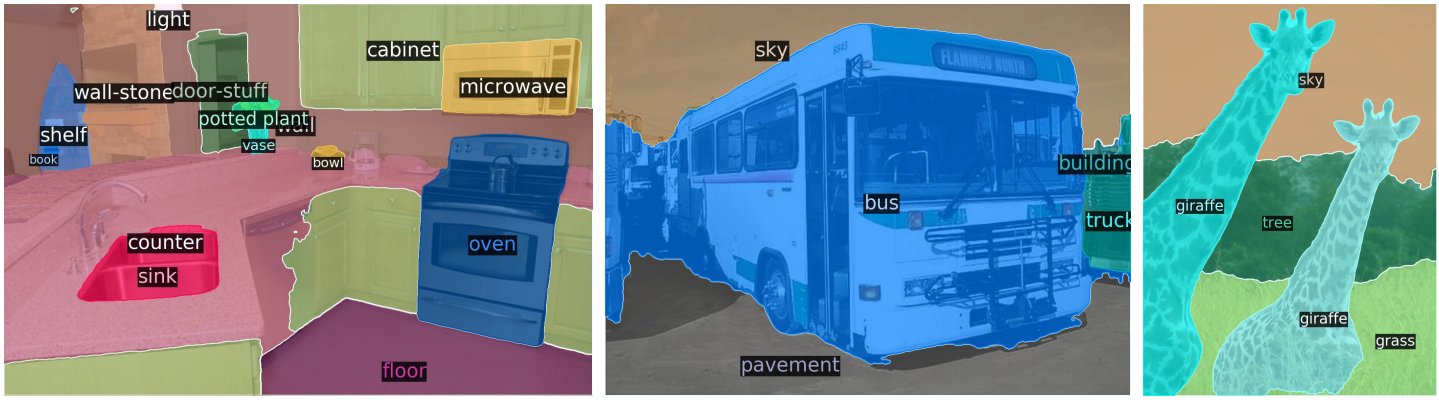
다음은 DETR-R101에 의해 생성된 panoptic segmentation 결과이다.