[논문리뷰] Depth Pro: Sharp Monocular Metric Depth in Less Than a Second
ICLR 2025. [Paper] [Github]
Aleksei Bochkovskii, Amaël Delaunoy, Hugo Germain, Marcel Santos, Yichao Zhou, Stephan R. Richter, Vladlen Koltun
Apple
2 Oct 2024

Introduction
본 논문은 zero-shot monocular depth estimation에 초점을 맞춘 연구이다. 특히 단일 이미지에서의 novel view synthesis에 대한 여러 가지 요구 사항에 초점을 맞추었다.
- Depth estimator는 특정 도메인에 제한되지 않고 모든 이미지에서 zero-shot으로 작동해야 한다. 나아가 카메라 intrinsic이 제공되지 않더라도 absolute scale을 갖는 metric depth map을 생성해야 한다.
- 설득력 있는 결과를 얻으려면 depth estimator가 고해상도로 작동하고 머리카락이나 털과 같은 이미지 디테일에 밀접하게 관련되는 세밀한 depth map을 생성해야 한다.
- 많은 대화형 애플리케이션 시나리오에서 depth estimator는 고해상도 이미지를 1초 이내에 처리하여 필요에 따라 대화형 뷰 합성 “쿼리”들을 지원해야 한다.
본 논문에서는 이러한 모든 요구 사항을 충족하는 zero-shot metric depth estimation을 위한 foundation model인 Depth Pro를 제시하였다. Depth Pro의 특징은 다음과 같다.
- 카메라 intrinsic 없이도 임의의 이미지에 대한 absolute scale을 갖는 metric depth map을 생성한다.
- V100 GPU에서 0.3초 만에 1536$\times$1536 해상도의 depth map을 생성한다.
- 머리카락, 털, 식물과 같은 미세한 구조를 포함하여 물체 경계의 선명한 묘사 능력이 이전 방법들을 획기적으로 능가한다.
Depth Pro는 여러 가지 기술적 기여를 통해 가능해졌다.
- 글로벌 이미지 컨텍스트를 캡처하는 동시에 고해상도에서 미세 구조를 유지하기 위한 효율적인 멀티스케일 ViT 기반 아키텍처를 사용한다.
- Monocular depth map을 평가할 때 경계 추적의 정확도를 정량화하기 위해 매우 정확한 매팅 데이터셋을 활용할 수 있는 새로운 metric을 도출하였다.
- 현실 데이터셋은 경계 주변이 부정확하고, 합성 데이터셋은 정확한 픽셀 단위 GT를 제공하지만 사실성이 제한된다. 둘 모두로 학습하기 위해 선명한 깊이 추정을 촉진하는 loss 함수들과 학습 커리큘럼을 고안하였다.
- 단일 이미지에서 zero-shot 초점 거리 추정을 제공한다.
Method
1. Network
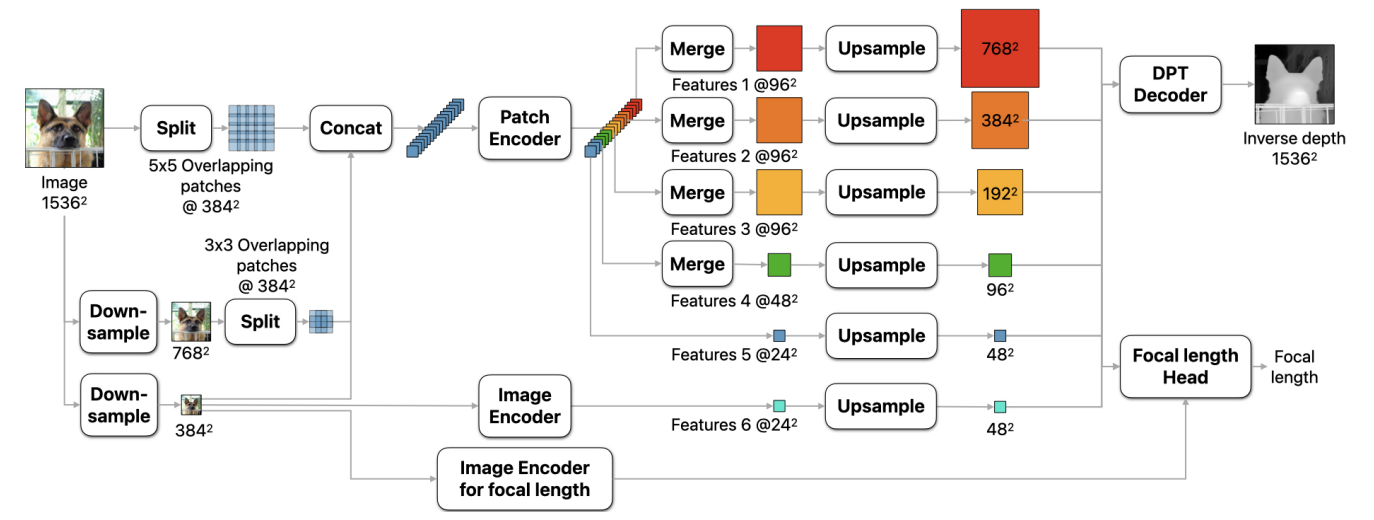
아키텍처의 핵심 아이디어는 여러 스케일에서 추출된 패치에 일반 ViT 인코더를 적용하고 패치 예측을 end-to-end로 학습 가능한 모델에서 하나의 고해상도 예측으로 융합하는 것이다. 깊이를 예측하기 위해 두 가지 ViT 인코더를 사용한다.
- 패치 인코더: 여러 스케일에서 추출된 패치에 적용된다. 이를 통해 가중치가 스케일 간에 공유되므로 학습 표현이 scale-invariant하게 된다.
- 이미지 인코더: 패치 예측을 글로벌 컨텍스트에 고정한다. 전체 입력 이미지를 인코더 backbone의 기본 입력 해상도인 384$\times$384로 다운샘플링한 후 인코더에 입력한다.
전체 네트워크는 1536$\times$1536의 고정 해상도에서 작동한다. 이를 통해 모든 이미지에 대해 충분히 큰 receptive field와 일정한 실행 시간이 보장되고 메모리 부족 오류가 방지된다. Depth Pro는 가변 해상도 방식보다 수십 배 더 빠르면서도 더 정확하고 더 선명한 경계를 생성한다. 커스텀 인코더 대신 일반 ViT 인코더를 사용하기 때문에 활용할 수 있는 사전 학습된 ViT 기반 backbone이 풍부하다.
1536$\times$1536으로 다운샘플링한 후 입력 이미지를 384$\times$384 패치로 분할한다. 두 개의 가장 fine한 스케일의 경우, 이어붙인 자국이 생기는 것을 피하기 위해 패치를 겹쳐 놓는다. 각 스케일에서 패치는 패치 인코더에 입력되고, 입력 패치당 24$\times$24 해상도의 feature 텐서를 생성한다. 가장 fine한 스케일에서 중간 feature를 추가로 추출하여 더 세밀한 디테일을 캡처한다. Feature 패치를 병합하여 DPT 디코더와 유사한 디코더 모듈에 입력한다.
ViT의 multi-head self-attention은 입력 픽셀 수의 제곱에 비례하는 계산 복잡도, 즉 이미지 차원의 네제곱에 비례하는 계산 복잡도를 가진다. 따라서 패치 기반 처리로 인해 계산을 훨씬 효율적으로 할 수 있다. 또한, 패치를 독립적으로 처리할 수 있으므로 병렬화가 가능하다.
2. Sharp monocular depth estimation
목적 함수
각 입력 이미지 $I$에 대해 네트워크 $f$는 canonical inverse depth 이미지 $C = f(I)$를 예측한다. Dense한 metric depth map $D_m$을 얻기 위해 초점 거리 \(f_\textrm{px}\)와 너비 $w$로 수평 시야각으로 크기를 조정한다.
\[\begin{equation} D_m = \frac{f_\textrm{px}}{wC} \end{equation}\]여러 목적 함수는 모두 canoncial inverse depth를 기반으로 한다. 왜냐하면 canoncial inverse depth는 카메라에 가까운 영역을 더 먼 영역이나 전체 장면보다 우선시하고, 따라서 novel view synthesis (NVS)와 같은 애플리케이션에서 시각적 품질을 지원하기 때문이다.
모든 metric 데이터셋에 대해 픽셀별 mean absolute error를 계산한다. 합성 데이터셋과 달리 현실 데이터셋의 경우, 이미지별로 상위 20%의 오차가 있는 픽셀을 버린다.
\[\begin{equation} \mathcal{L}_\textrm{MAE} (\hat{C}, C) = \frac{1}{N} \sum_i^N \vert \hat{C}_i - C_i \vert \end{equation}\]($i$는 픽셀, $\hat{C}$는 GT canoncial inverse depth)
Non-metric 데이터셋, 즉 신뢰할 수 있는 카메라 intrinsic이 없거나 스케일이 일관되지 않은 데이터셋의 경우, loss를 적용하기 전에 중앙값으로부터 평균 절대 편차를 통해 예측과 GT를 정규화한다. 또한 여러 스케일에서 canoncial inverse depth map들의 1차 및 2차 미분에 대한 오차를 계산한다. $M$개의 스케일에 대한 멀티스케일 미분 loss를 다음과 같이 정의한다.
\[\begin{equation} \mathcal{L}_{\ast, p, M} (C, \hat{C}) = \frac{1}{M} \sum_j^M \frac{1}{N_j} \sum_i^{N_j} \vert \nabla_\ast C_i^j - \nabla_\ast \hat{C}_i^j \vert^p \end{equation}\]($\ast$는 Scharr(S) 또는 Laplace(L)와 같은 공간 미분 연산자, $p$는 norm)
Scale $j$는 scale당 2배씩 inverse depth map을 흐리게 처리하고 다운샘플링하여 계산된다.
- Mean Absolute Gradient Error \(\mathcal{L}_\textrm{MAGE} = \mathcal{L}_{S,1,6}\)
- Mean Absolute Laplace Error \(\mathcal{L}_\textrm{MALE} = \mathcal{L}_{L,1,6}\)
- Mean Squared Gradient Error \(\mathcal{L}_\textrm{MSGE} = \mathcal{L}_{S,2,6}\)
학습 커리큘럼
저자들은 다음과 같은 관찰 결과를 바탕으로 학습 커리큘럼을 제안하였다.
- 현실 데이터셋과 합성 데이터셋의 대규모 혼합에 대한 학습은 zero-shot 정확도, 즉 일반화를 개선한다.
- 합성 데이터셋은 픽셀 정확도의 GT를 제공하는 반면, 현실 데이터셋은 종종 누락된 영역, 불일치하는 깊이, 물체 경계에 대한 잘못된 측정을 포함한다.
- 예측은 학습 과정에서 더 선명해진다.
저자들은 이러한 관찰을 바탕으로 2단계 학습 커리큘럼을 설계하였다. 첫 번째 단계에서는 네트워크가 도메인 간에 일반화할 수 있도록 하는 robust한 feature를 학습하는 것을 목표로 한다. 이를 위해 레이블이 있는 모든 학습 세트를 혼합하여 학습한다. 구체적으로, metric 데이터셋에서는 \(\mathcal{L}_\textrm{MAE}\)를 최소화하고 non-metric 데이터셋에서는 정규화된 버전을 최소화한다. \(\mathcal{L}_\textrm{MAE}\)는 손상된 실제 GT를 처리하는 데 있어 robust하기 때문에 선택되었다.
네트워크를 선명한 경계로 유도하기 위해 예측의 gradient에 대한 loss도 포함한다. 그러나 단순하게 적용하면 최적화를 방해하고 수렴 속도를 늦출 수 있다. 저자들은 합성 데이터셋에만 적용된 gradient에 대한 scale-and-shift-invariant loss가 가장 효과적이라는 것을 발견했다.
두 번째 단계의 학습은 경계를 선명하게 하고 예측된 depth map에서 디테일을 드러내도록 설계되었다. 부정확한 GT의 영향을 최소화하기 위해 이 단계에서는 고품질의 픽셀 수준 GT를 제공하는 합성 데이터셋에 대해서만 학습한다. 구체적으로, \(\mathcal{L}_\textrm{MAE}\)를 다시 최소화하고 멀티스케일 미분 loss를 추가로 사용한다.
선명한 경계에 대한 평가 metric
Monocular depth estimation을 위한 일반적인 벤치마크는 경계 선명도를 거의 고려하지 않는다. 이는 정밀한 픽셀 수준의 GT 깊이를 가진 다양하고 현실적인 데이터셋이 부족하기 때문일 수 있다.
저자들은 이러한 단점을 해결하기 위해 깊이 경계를 평가하기 위한 새로운 metric을 제안하였다. 주요 아이디어는 기존의 matting, saliency, segmentation을 위한 고품질 주석을 깊이 경계에 대한 GT로 활용할 수 있다는 것이다. 이러한 주석들을 전경/배경 관계를 정의하는 binary map으로 처리한다. 관계가 유지되도록 binary map에서 가장자리 주변의 픽셀만 고려한다.
Ranking loss에 의해 동기를 부여받아, 주변 픽셀의 쌍별 깊이 비율을 사용하여 전경/배경 관계를 정의한다. $i$와 $j$를 두 주변 픽셀의 위치라 하자. 그러면 depth map $d$에서 파생된 occluding contour $c_d$를
\[\begin{equation} c_d (i, j) = \begin{cases} 1 & \; \frac{d(j)}{d(i)} > \bigg( 1 + \frac{t}{100} \bigg) \\ 0 & \; \textrm{otherwise} \end{cases} \end{equation}\]로 정의한다. 이는 해당 깊이가 $t$% 이상 차이가 나는 경우 픽셀 $i$와 $j$ 사이에 occluding contour가 있음을 나타낸다. 주변 픽셀의 모든 쌍에 대해 precision $P$와 recall $R$을 다음과 같이 계산할 수 있다.
\[\begin{aligned} P(t) &= \frac{\sum_{i,j \in N(i)} c_d (i,j) \wedge c_{\hat{d}} (i,j)}{\sum_{i,j \in N(i)} c_d (i,j)} \\ R(t) &= \frac{\sum_{i,j \in N(i)} c_d (i,j) \wedge c_{\hat{d}} (i,j)}{\sum_{i,j \in N(i)} c_{\hat{d}} (i,j)} \end{aligned}\]$P$와 $R$은 모두 scale-invariant하며, 실험에서는 F1 score로 평가하였다. 여러 상대적 깊이 비율을 설명하기 위해 \(t_\textrm{min} = 5\)에서 \(t_\textrm{max} = 25\)까지 선형적인 threshold를 사용하여 F1 score의 가중 평균을 추가로 계산하며, 높은 threshold에 더 강한 가중치를 둔다. 다른 edge 기반 metric과 비교했을 때, 본 논문의 metric은 edge에 대한 주석이 필요하지 않으며, 합성 데이터셋에서 쉽게 얻을 수 있는 픽셀 단위의 GT만 필요하다.
마찬가지로, matting, saliency, segmentation를 위한 현실 데이터셋에서 파생될 수 있는 binary mask에서 occluding contour를 식별할 수도 있다. 이미지 위에 binary mask $b$가 주어지면 픽셀 $i$와 $j$ 사이에 occluding contour $c_b$의 존재 여부를 \(c_b (i, j) = b(i) \wedge \neg b(j)\)로 정의한다. 이 정의를 바탕으로 $c_d$를 $c_b$로 대체하여 recall $R(t)$를 계산한다.
Binary map은 일반적으로 전체 물체를 레이블링하므로 물체 실루엣과 일치하지 않는 GT occluding contour를 얻을 수 없다. 따라서 경계 주석은 불완전하다. 이 절차로 일부 occluding contour를 식별할 수 있지만 모든 occluding contour는 식별할 수 없다. 따라서 binary map에 대한 recall만 계산할 수 있고 precision은 계산할 수 없다.
흐릿한 edge에 대한 페널티를 부과하기 위해, \(c_{\hat{d}} (i,j)\) 연결 요소(connected component)의 유효한 경계 내에서 \(c_{\hat{d}}\) 값에 non-maximum suppression (NMS)를 적용한다.
3. Focal length estimation
EXIF 메타데이터가 부정확하거나 누락된 이미지를 처리하기 위해 초점 거리를 추정하는 head로 네트워크를 보완한다. 작은 convolutional head는 깊이 추정 네트워크에서 고정된 feature를 수집하고 별도의 ViT 이미지 인코더에서 task별 feature를 수집하여 수평 FOV를 예측한다. 이 때, 학습 loss로 \(\mathcal{L}_2\)를 사용한다.
깊이 추정 학습 후 초점 거리 head와 ViT 인코더를 학습시킨다. 초점 거리 학습을 분리하면 깊이 네트워크와의 공동 학습에 비해 여러 가지 이점이 있다.
- 깊이 loss와 초점 거리 loss의 균형을 맞출 필요가 없다.
- 깊이 추정 네트워크를 학습시킬 때 사용되는 일부 좁은 도메인의 단일 카메라 데이터셋을 제외하고, 초점 거리 head를 다른 데이터셋으로 학습시킬 수 있게 해준다.
- 깊이 supervision 없이 초점 거리 supervision을 제공하는 대규모 이미지 데이터셋을 추가할 수 있다.
Experiments
다음은 경계 정확도와 실행 시간을 비교한 그래프이다.
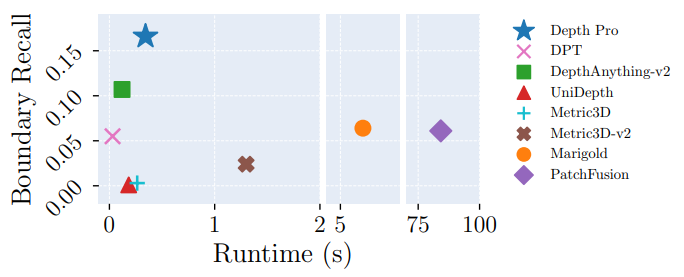
다음은 zero-shot metric depth 정확도를 비교한 결과이다.
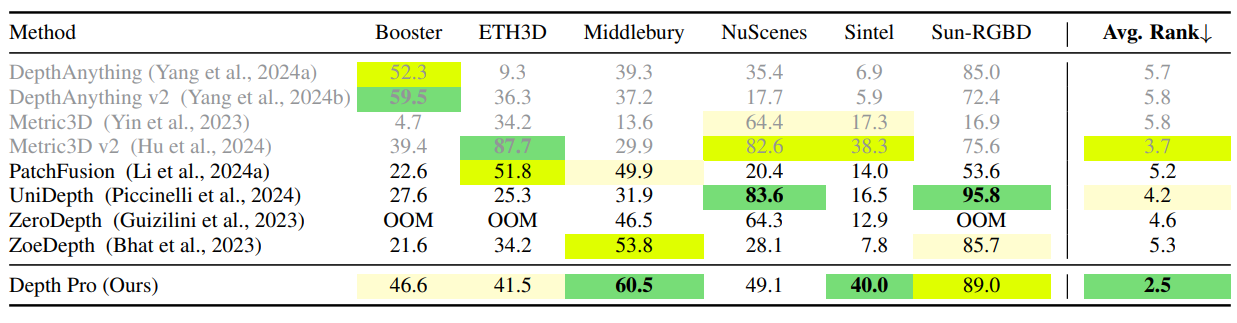
다음은 zero-shot 경계 정확도를 비교한 결과이다.
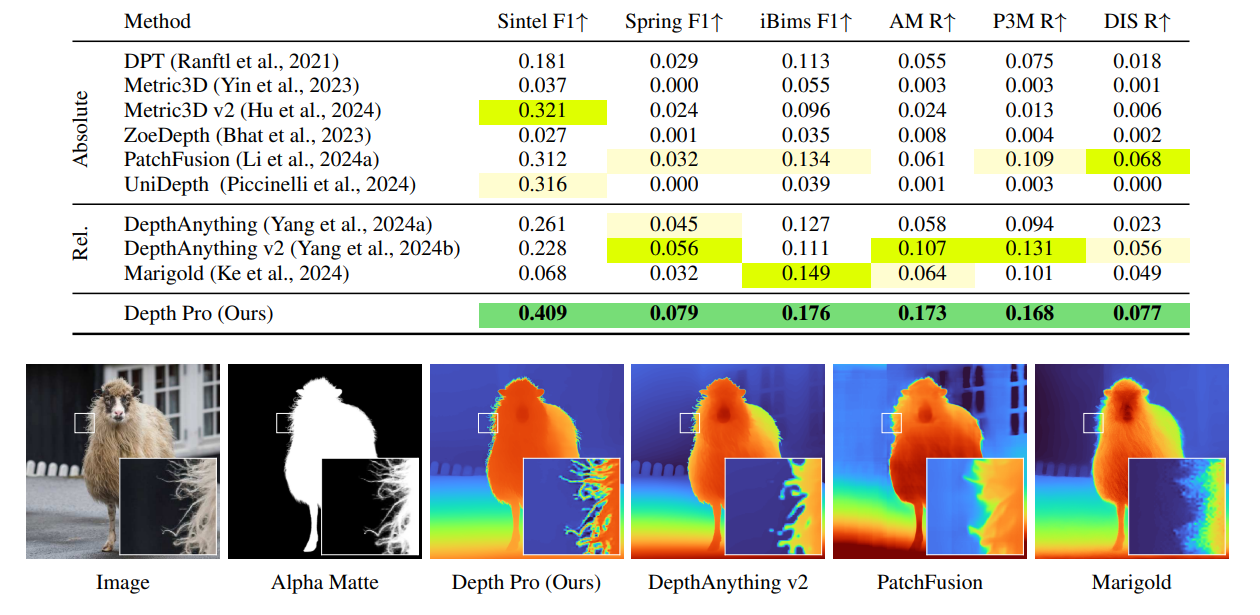
다음은 생성된 depth map을 novel view synthesis 시스템인 TMPI에 적용한 결과를 비교한 것이다.

다음은 초점 거리 추정 결과를 비교한 것이다. \(\delta_\textrm{25%}\)와 \(\delta_\textrm{50%}\)는 초점 거리의 상대 오차가 각각 25%와 50%보다 작은 이미지의 비율(%)이다.
