[논문리뷰] Depth Anything 3: Recovering the Visual Space from Any Views
arXiv 2025. [Paper] [Page] [Github]
Haotong Lin, Sili Chen, Junhao Liew, Donny Y. Chen, Zhenyu Li, Guang Shi, Jiashi Feng, Bingyi Kang
ByteDance Seed
13 Nov 2025
Introduction
본 논문에서는 기존의 3D task 정의에서 벗어나 보다 근본적인 목표, 즉 단일 이미지, 장면의 여러 시점, 또는 동영상 스트림 등 임의의 비전 입력으로부터 3D 구조를 복원하는 목표로 돌아갔다. 저자들은 두 가지 핵심 질문을 기반으로 하는 최소 모델링 전략을 추구하였다.
- 최소한의 예측 타겟 집합이 존재하는가, 아니면 여러 3D task에 걸친 공동 모델링이 필요한가?
- 하나의 transformer만으로 이 목표에 충분할 수 있는가?
본 논문은 두 가지 질문에 모두 긍정적인 답을 제시하였다. 광선 표현을 통해 공동으로 모든 시점 깊이 및 포즈를 추정하는 단일 transformer 모델인 Depth Anything 3를 제시하였다. 저자들은 이 최소한의 접근법이 알려진 카메라 포즈의 유무와 관계없이 여러 이미지로부터 공간을 재구성하는 데 충분함을 보여주었다.
Depth Anything 3는 기하학적 재구성 타겟을 dense prediction task로 취급한다. 주어진 $N$개의 입력 이미지 세트에 대해, 모델은 각 픽셀이 해당 입력 이미지와 정렬된 $N$개의 해당 depth map과 ray map을 출력하도록 학습된다. 이를 위한 아키텍처는 강력한 feature 추출 기능을 활용하는 사전 학습된 ViT를 backbone으로 사용한다. 임의의 뷰 수를 처리하기 위해, input-adaptive cross-view self-attention 메커니즘이라는 핵심 수정 사항을 도입하였다. 이 모듈은 선택된 레이어의 forward pass 중에 토큰을 동적으로 재배열하여 모든 뷰에서 효율적인 정보 교환을 가능하게 한다. 최종 예측을 위해, 저자들은 동일한 feature 세트를 서로 다른 융합 파라미터로 처리하여 depth map과 ray map을 모두 공동으로 출력하도록 설계된 새로운 Dual-DPT head를 제안하였다. 유연성을 높이기 위해, 모델은 간단한 카메라 인코더를 통해 알려진 카메라 포즈를 선택적으로 통합하여 다양한 실제 설정에 적응할 수 있다. 이러한 전반적인 설계는 사전 학습된 backbone의 scaling 속성을 직접 상속하는 깔끔하고 scalable한 아키텍처를 구현한다.
저자들은 다양한 학습 데이터를 통합하기 위해 teacher-student 패러다임을 통해 Depth Anything 3를 학습시켰는데, 이는 generalist model에 필수적이다. 데이터 소스에는 실제 깊이 카메라 캡처, 3D 재구성, 합성 데이터와 같은 다양한 형식이 포함되어 있으며, 실제 데이터에서는 깊이의 품질이 떨어질 수 있다. 이 문제를 해결하기 위해 pseudo-labeling 전략을 사용한다. 구체적으로, 모든 실제 데이터에 대해 dense하고 고품질인 pseudo depth를 생성하기 위해 합성 데이터를 기반으로 강력한 teacher monocular depth 모델을 학습시켰다. 중요한 것은 기하학적 무결성을 유지하기 위해 이러한 dense pseudo-depth map을 원래의 sparse하거나 노이즈가 있는 depth map과 정렬한다는 것이다. 이 접근법은 기하학적 정확도를 희생하지 않으면서도 레이블의 디테일과 완전성을 크게 향상시켜 매우 효과적인 것으로 입증되었다.
추가로, 저자들은 feed-forward novel view synthesis (FF-NVS)를 위해, 픽셀 정렬된 3D Gaussian 파라미터를 예측하는 추가 DPT head를 도입하고 fine-tuning시켰다. Depth Anything 3의 강력한 성능으로 인해 기존 모델들보다 더 높은 성능을 보여주었다.
Depth Anything 3
1. Formulation
입력으로 \(\mathcal{I} = \{\textbf{I}_i \in \mathbb{R}^{H \times W \times 3}\}_{i=1}^{N_v}\)가 주어진다. $N_v = 1$인 경우 monocular 이미지이고 $N_v > 1$인 경우 동영상 또는 멀티뷰 세트이다. 각 이미지는 깊이 \(\textbf{D}_i \in \mathbb{R}^{H \times W}\), 카메라 extrinsic \([\textbf{R}_i \vert \textbf{t}_i]\), intrisic \(\textbf{K}_i\)를 갖는다. 카메라는 \(\textbf{v}_i \in \mathbb{R}^9\)로 표현할 수도 있으며, 이때 translation \(\textbf{t}_i \in \mathbb{R}^3\), rotation quaternion \(\textbf{q}_i \in \mathbb{R}^4\), FOV 파라미터 \(\textbf{f}_i \in \mathbb{R}^2\)이다. 픽셀 $\textbf{p} = (u, v, 1)^\top$는 3D 포인트 $\textbf{P} = (X, Y, Z, 1)^\top$로 projection된다.
\[\begin{equation} \textbf{P} = \textbf{R}_i (\textbf{D}_i (u, v) \textbf{K}_i^{-1} \textbf{p}) + \textbf{t}_i \end{equation}\]Depth-ray 표현
유효한 회전 행렬 \(\textbf{R}_i\)를 예측하는 것은 orthogonality 제약으로 인해 어렵다. 이를 방지하기 위해 입력 이미지와 depth map에 맞춰 정렬된 per-pixel ray map을 사용하여 카메라 포즈를 암시적으로 표현한다. 각 픽셀 $\textbf{p}$에 대해 카메라 광선 $\textbf{r} = (\textbf{t}, \textbf{d}) \in \mathbb{R}^6$은 원점 $\textbf{t} \in \mathbb{R}^3$와 방향 $\textbf{d} \in \mathbb{R}^3$으로 정의된다. 방향은 $\textbf{p}$를 카메라 프레임으로 backprojection하고 월드 프레임으로 회전하여 얻는다.
\[\begin{equation} \textbf{d} = \textbf{R} \textbf{K}^{-1} \textbf{p} \end{equation}\]Dense ray map $\textbf{M} \in \mathbb{R}^{H \times W \times 6}$은 모든 픽셀에 대해 이러한 파라미터를 저장한다. $\textbf{d}$를 정규화하지 않으므로 크기는 projection scale을 유지한다. 따라서 월드 프레임의 3D 포인트는 간단히
\[\begin{equation} \textbf{P} = \textbf{t} + \textbf{D}(u,v) \cdot \textbf{d} \end{equation}\]이다. 이 공식은 element-wise 연산을 통해 예측된 depth map과 ray map을 결합하여 일관된 포인트 클라우드를 생성할 수 있도록 한다.
Ray map에서 카메라 파라미터 유도
Ray map $\textbf{M} \in \mathbb{R}^{H \times W \times 6}$은 처음 세 채널에 저장된 픽셀별 광선 원점과 마지막 세 채널에 저장된 광선 방향으로 구성된다.
먼저, 카메라 중심 \(\textbf{t}_c\)는 픽셀별 광선 원점 벡터를 평균하여 추정된다.
\[\begin{equation} \textbf{t}_c = \frac{1}{HW} \sum_{h=1}^H \sum_{w=1}^W \textbf{M} (h, w, :3) \end{equation}\]Rotation $\textbf{R}$과 intrisic $\textbf{K}$를 추정하기 위해 문제를 homography $\textbf{H}$를 찾는 것으로 구성한다. 먼저 intrisic이 항등 행렬 $\textbf{K}_I = \textbf{I}$인 identity 카메라를 정의한다. 주어진 픽셀 $\textbf{p}$에 대해, 이 표준 카메라 좌표계에서 광선 방향은 간단히 \(\textbf{d}_I = \textbf{p}\)이다. 이 표준 광선 \(\textbf{d}_I\)에서 타겟 카메라 좌표계에서의 광선 방향 \(\textbf{d}_\textrm{cam}\)으로의 변환은 \(\textbf{d}_\textrm{cam} = \textbf{K} \textbf{R} \textbf{d}_I\)로 주어진다. 이는 두 광선 집합 사이에 직접적인 homography 관계 $\textbf{H} = \textbf{K}\textbf{R}$을 설정한다. 그런 다음 변환된 표준 광선과 미리 계산된 타겟 광선 집합 $\textbf{M}(h, w, 3 :)$ 사이의 기하학적 오차를 최소화하여 이 homography를 구할 수 있다. 이는 다음과 같은 최적화 문제로 이어진다.
\[\begin{equation} \textbf{H}^\ast = \underset{\| \textbf{H} \| = 1}{\arg \min} \sum_{h=1}^H \sum_{w=1}^W \| \textbf{H} \textbf{p}_{h,w} \times \textbf{M}(h, w, 3:) \| \end{equation}\]이는 Direct Linear Transform (DLT) 알고리즘을 사용하여 효율적으로 풀 수 있는 표준 least-squares 문제이다. 최적의 homography $\textbf{H}^\ast$를 찾으면 카메라 파라미터를 복구한다. $\textbf{K}$는 upper-triangular matrix이고 $\textbf{R}$은 orthonormal matrix이므로, $\textbf{H}^\ast$에 RQ decomposition을 사용하여 $\textbf{K}$와 $\textbf{R}$을 고유하게 얻을 수 있다.
최소한의 예측 타겟
최근 연구들에서는 다양한 3D task에 대한 통합 모델을 구축하는 것을 목표로 하며, 종종 다른 타겟을 사용한 multitask 학습을 사용한다. 예를 들어, point map만 사용하거나 포즈, 로컬/글로벌 point map, depth map의 중복 조합을 사용한다. Point map만으로는 일관성을 보장하기에 충분하지 않으며, 중복 타겟은 포즈 정확도를 향상시킬 수 있지만 종종 일관성을 손상시킨다.
반대로, depth-ray 표현은 장면 구조와 카메라 모션을 모두 캡처하는 데 최소이면서도 충분한 타겟 세트를 형성하여 point map이나 더 복잡한 출력과 같은 대안보다 성능이 우수하다. 그러나 inference 시에 ray map에서 카메라 포즈를 복구하는 것은 계산적으로 비용이 많이 든다. 저자들은 가벼운 카메라 head인 $\mathcal{D}_C$를 추가하여 이 문제를 해결하였다. 이 transformer는 카메라 토큰에서 작동하여 FOV \(\textbf{f} \in \mathbb{R}^2\), rotation quaternion \(\textbf{q} \in \mathbb{R}^4\), translation \(\textbf{t} \in \mathbb{R}^3\)을 예측한다. 뷰당 하나의 토큰만 처리하므로 추가 비용은 무시할 수 있다.
2. Architecture
네트워크는 세 가지 주요 구성 요소로 이루어져 있다.
- Backbone 역할을 하는 transformer 모델
- 포즈 컨디셔닝을 위한 선택적 카메라 인코더
- 예측을 생성하는 Dual-DPT head
Transformer backbone
대규모 monocular 이미지 코퍼스에서 사전 학습된 $L$개의 블록이 있는 DINOv2를 사용한다. 입력 토큰을 재배열하여 구현된 input-adaptive self-attention을 통해 아키텍처 변경 없이 cross-view 추론이 가능하다. 저자들은 transformer를 $L_s$와 $L_g$의 두 그룹으로 나누었다 ($L = L_s + L_g$). 처음 $L_s$개의 layer는 각 이미지 내에서 self-attention을 적용하는 반면, 이후 $L_g$개의 layer는 텐서 재정렬을 통해 모든 토큰에 공동으로 작동하면서 뷰 사이의 attention과 뷰 내의 attention을 번갈아 가며 작동한다. 실제로는 $L_s : L_g = 2 : 1$로 설정한다. 이 구성은 다른 배열에 비해 성능과 효율성 간에 최적의 균형을 제공한다.
카메라 조건 주입
포즈를 아는 입력 이미지와 모르는 입력 이미지를 모두 원활하게 처리하기 위해 각 뷰 앞에 카메라 토큰 \(\textbf{c}_i\)를 추가한다. 카메라 파라미터 \((\textbf{K}_i, \textbf{R}_i, \textbf{t}_i)\)를 사용할 수 있는 경우, MLP \(\mathcal{E}_c\)를 통해 토큰을 얻는다.
\[\begin{equation} \textbf{c}_i = \mathcal{E}_c (\textbf{f}_i, \textbf{q}_i, \textbf{t}_i) \end{equation}\]그렇지 않은 경우, 학습 가능한 공유 토큰 \(\textbf{c}_l\)이 사용된다. 패치 토큰과 concat된 이러한 카메라 토큰은 모든 attention 연산에 참여하여 명시적인 기하학적 컨텍스트 또는 일관된 placeholder를 제공한다.
Dual-DPT head
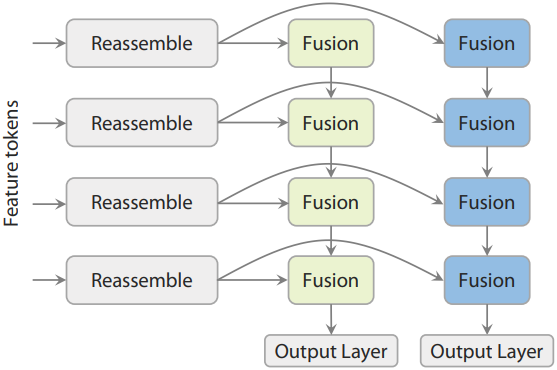
최종 예측 단계에서는 Dual-DPT head를 통해 dense depth map과 dense ray map을 함께 생성한다. 이 설계는 강력하면서도 효율적이다. Backbone에서 feature 세트를 받으면, Dual-DPT head는 먼저 공유된 reassembly 모듈 집합을 통해 이를 처리한다. 이후, 처리된 feature들은 depth branch와 ray branch를 위한 두 개의 서로 다른 fusion layer 세트를 사용하여 융합된다. 마지막으로, 두 개의 개별 output layer는 최종 depth map 및 ray map 예측을 생성한다. 이러한 설계는 두 예측 task 간의 강력한 상호작용을 촉진하는 동시에 중복된 중간 표현을 방지한다.
3. Training
Teacher-student 학습 패러다임
학습 데이터는 실제 깊이 캡처, 3D 재구성, 합성 데이터셋 등 다양한 소스에서 수집된다. 실제 깊이는 노이즈가 많고 불완전한 경우가 많다. 이러한 문제를 해결하기 위해, 합성 데이터만을 사용하여 monocular relative depth를 추정하는 teacher 모델을 학습시켜 고품질의 pseudo-label을 생성한다. 이러한 가상 depth map은 RANSAC least squares를 통해 sparse하거나 노이즈가 있는 원본 GT 데이터와 정렬되어 레이블의 디테일과 완전성을 향상시키면서 기하학적 정확도를 유지한다. 이 모델을 Depth-Anything-3-Teacher라고 부르며, 대규모 합성 코퍼스를 기반으로 학습시켜 세밀한 geometry를 포착한다.
학습 loss
모델 \(\mathcal{F}_\theta\)는 입력 $\mathcal{I}$를 depth map $\hat{\textbf{D}}$, ray map $\hat{\textbf{R}}$, 그리고 선택적 카메라 포즈 $\hat{\textbf{c}}$로 구성된 출력 집합에 매핑한다.
\[\begin{equation} \mathcal{F}_\theta = \mathcal{I} \mapsto \{ \hat{\textbf{D}}, \hat{\textbf{R}}, \hat{\textbf{c}} \} \end{equation}\]Loss 계산에 앞서 모든 GT 신호는 공통 scale factor로 정규화된다. 이 scale은 reprojection된 point map $\textbf{P}$의 평균 \(\ell_2\) norm으로 정의되며, 이는 다양한 모달리티에서 일관된 크기를 보장하고 학습 과정을 안정화한다. 전체 학습 loss는 여러 항의 가중 합으로 정의된다.
\[\begin{equation} \mathcal{L} = \mathcal{L}(\hat{\textbf{D}}, \textbf{D}) + \mathcal{L}_M (\hat{\textbf{R}}, \textbf{M}) + \mathcal{L}_P (\hat{\textbf{D}} \odot \textbf{d} + \textbf{t}, \textbf{P}) + \mathcal{L}_C (\hat{\textbf{c}}, \textbf{v}) + \mathcal{L}_\textrm{grad} (\hat{\textbf{D}}, \textbf{D}) \\ \mathcal{L}(\hat{\textbf{D}}, \textbf{D}; D_c) = \frac{1}{Z_\Omega} \sum_{p \in \Omega} m_p (D_{c,p} \vert \hat{\textbf{D}}_p - \textbf{D}_p \vert - \lambda_c \log D_{c,p}) \\ \mathcal{L}_\textrm{grad} (\hat{\textbf{D}}, \textbf{D}) = \| \nabla_x \hat{\textbf{D}} - \nabla_x \textbf{D} \|_1 + \| \nabla_y \hat{\textbf{D}} - \nabla_y \textbf{D} \|_1 \end{equation}\]($D_{c,p}$는 \(\textbf{D}_p\)의 신뢰도, 모든 loss 항은 \(\ell_1\) norm 기반)
4. Implementation Details
- GPU: H100 128개
- iteration: 20만
- 12만 iteration부터 GT depth 대신 teacher 모델의 pseudo-label 사용
- learning rate: $2 \times 10^{-4}$ (8k warm-up)
- 기본 해상도: 504$\times$504
- 뷰 수: $[2, 18]$에서 샘플링됨
- 포즈 컨디셔닝 확률: 0.2
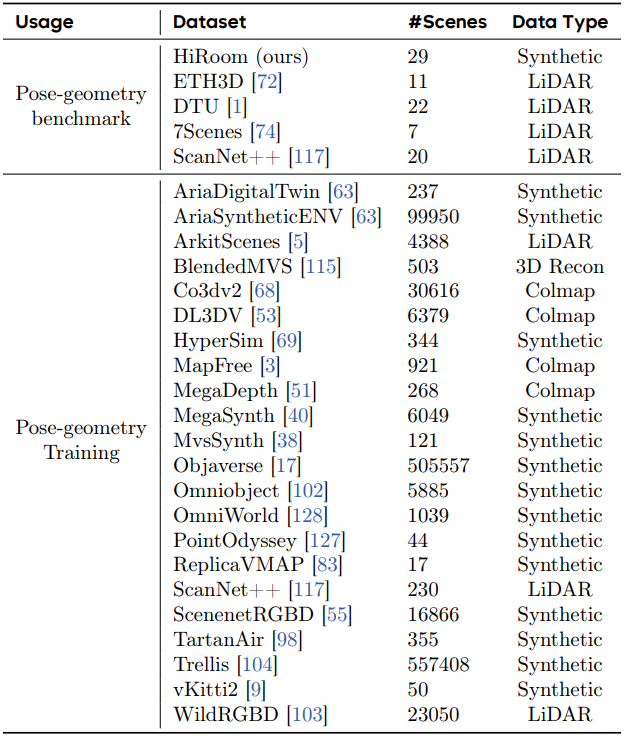
학습에 사용된 데이터셋은 아래 표와 같다.
Teacher-Student Learning
실제 데이터는 품질이 좋지 않으므로, 실제 데이터에 대한 supervision을 제공하기 위해 합성 데이터만을 사용하여 teacher 모델을 학습시킨다. Teacher 모델은 monocular relative depth를 추정하도록 학습된다. 실제 데이터의 GT depth에서 scale 및 shift 파라미터를 계산하고, 이를 통해 예측된 relative depth와 metric depth 측정값을 일치시킬 수 있다.
1. Constructing the Teacher Model
저자들은 Depth Anything 2 (DA2)를 기반으로 데이터와 표현을 포함한 여러 핵심 측면에서 모델을 확장시켰다. 학습 코퍼스를 확장하면 깊이 추정 성능이 크게 향상되어 데이터 scaling의 이점을 보인다. 또한, 수정된 깊이 표현이 표준 2D 평가 지표에서 눈에 띄는 개선을 보이지는 않지만, 기하학적 왜곡이 적고 장면 구조가 더욱 사실적으로 표현되는 등 질적으로 향상된 3D 포인트 클라우드를 제공한다. Teacher 모델의 backbone은 DA3 프레임워크(DINOv2 ViT + DPT 디코더)와 직접 연계되어 있으며, 특별한 아키텍처 수정은 도입되지 않았다.
깊이 표현
Scale–shift-invariant disparity를 예측하는 DA2와 달리, teacher 모델은 scale–shift-invariant depth를 출력한다. Depth는 disparity보다는 깊이 공간에서 직접 연산되는 metric depth estimation 및 멀티뷰 geometry와 같은 후속 task에서 더 선호된다. 저자들은 disparity에 비해 카메라 근처 영역에서 깊이의 민감도가 떨어지는 문제를 해결하기 위해, linear depth 대신 exponential depth를 예측하여 짧은 거리에서의 변별력을 향상시켰다.
학습 loss
표준 depth-gradient loss 외에도, 저자들은 MoGe에서 도입된 global–local loss를 사용하는 ROE alignment를 채택하였다.
추가로, 로컬 geometry를 더욱 정교하게 조정하기 위해 distance-weighted surface normal loss를 도입하였다. 각 중심 픽셀에 대해 네 개의 인접 포인트를 샘플링하고 정규화되지 않은 normal $n_i$를 계산한다. 그런 다음 이러한 normal에 다음과 같은 가중치를 적용한다.
\[\begin{equation} w_i = \sum_{j=0}^4 \| n_j \| - \| n_i \| \end{equation}\]이는 중심에서 멀리 떨어진 이웃의 기여도를 낮추어 실제 로컬 surface normal에 더 가까운 평균 normal을 생성한다.
\[\begin{equation} n_m = \sum_{i=0}^4 w_i \frac{n_i}{\| n_i \|} \end{equation}\]최종 normal loss는 다음과 같다.
\[\begin{equation} \mathcal{L}_N = \mathcal{E}(\hat{n}_m, n_m) + \sum_{i=0}^4 \mathcal{E}(\hat{n}_i, n_i) \end{equation}\]($\mathcal{E}$는 angular error)
물체만 있는 데이터셋의 하늘 영역과 배경 영역에서는 GT가 정의되지 않는다. 이러한 영역이 깊이 예측 성능을 저하시키는 것을 방지하고 후속 활용을 용이하게 하기 위해, MSE loss를 사용하여 깊이 출력에 맞춰 하늘 마스크와 물체 마스크를 공동으로 예측한다. 전체 학습 loss는 다음과 같다.
\[\begin{equation} \mathcal{L}_T = \alpha \mathcal{L}_\textrm{grad} + \mathcal{L}_\textrm{gl} + \mathcal{L}_N + \mathcal{L}_\textrm{sky} + \mathcal{L}_\textrm{obj} \end{equation}\]($\alpha = 0.5$, \(\mathcal{L}_\textrm{grad}\)는 gradient loss, \(\mathcal{L}_\textrm{gl}\)은 global–local loss, \(\mathcal{L}_\textrm{sky}\)는 sky-mask loss, \(\mathcal{L}_\textrm{obj}\)는 object-mask loss)
2. Teaching Depth Anything 3
실제 데이터셋은 카메라 포즈 추정을 일반화하는 데 필수적이지만, 명확한 깊이 정보를 제공하는 경우는 드물다. Depth Anything 3 Teacher는 고품질의 relative depth를 제공하며, 이를 노이즈가 많은 측정값과 정렬시킨다. Residual 중앙값의 평균 절대 편차와 동일한 inlier threshold를 사용하여 RANSAC least squares를 통해 scale $s$와 shift $t$를 추정한다.
\[\begin{equation} (\hat{s}, \hat{t}) = \underset{s > 0, t}{\arg \min} \sum_{p \in \Omega} m_p (s \tilde{\textbf{D}}_p + t - \textbf{D}_p)^2, \quad \textbf{D}^{T \rightarrow M} = \hat{s} \tilde{\textbf{D}} + \hat{t} \end{equation}\]($\tilde{\textbf{D}}$는 teacher의 relative depth, $\textbf{D}$는 sparse depth, $m_p$는 유효한 깊이에 대한 마스크)
정렬된 \(\textbf{D}^{T \rightarrow M}\)은 Depth Anything 3에 대해 일관된 scale과 포즈-깊이 일관성 있는 supervision을 제공하여 실제 데이터에 대한 일반화를 개선한다.
3. Teaching Monocular Model
저자들은 teacher–student 패러다임 하에 monocular depth 모델을 학습시켰다. DA2 프레임워크를 따라, teacher가 생성한 pseudo-label로 레이블이 없는 이미지에 대해 monocular student를 학습시켰다. DA2와의 주요 차이점은 예측 타겟으로, student는 depth map을 예측하는 반면, DA2는 disparity를 예측한다. Teacher에 사용한 것과 동일한 loss를 pseudo-label에 적용하여 student를 추가로 학습시켰다. Monocular depth 모델은 relative depth도 예측한다. 이 student 모델은 표준 monocular depth 벤치마크에서 SOTA 성능을 달성하였다.
4. Teaching Metric Model
저자들은 teacher 모델로 경계가 뚜렷한 metric depth estimation 모델을 학습시켰다. Metric3Dv2를 따라, 초점 거리 변화에 따른 깊이 모호성을 해결하기 위해 canonical camera space transformation을 적용하였다. 선명한 디테일을 확보하기 위해 teacher 모델의 예측값을 학습 레이블로 사용한다. Teacher 모델의 예측 깊이의 scale과 shift를 실제 데이터의 metric depth 레이블과 일치시켜 학습시켰다.
- 학습 데이터셋: Taskonomy, DIML (Outdoor), DDAD, Argoverse, Lyft, PandaSet, Waymo, ScanNet++, ARKitScenes, Map-free, DSEC, Driving Stereo, Cityscapes
- 스테레오 데이터셋의 경우, FoundationStereo로 학습 레이블 생성
- 구현 디테일
- 학습 loss: \(\mathcal{L}_\textrm{depth}\), \(\mathcal{L}_\textrm{grad}\), \(\mathcal{L}_\textrm{sky}\)의 가중합
- 기본 해상도: 504$\times$504
- canonical focal length: $f_c = 300$
- optimizer: AdamW
- learning rate: 인코더 $5 \times 10^{-6}$, 디코더 $5 \times 10^{-5}$
- 5%의 확률로 random rotation augmentation
- 20%의 확률로 원래의 GT 레이블 사용
- batch size: 64
- iteration: 16만
Application: Feed-Forward 3D Gaussian Splattings
- 데이터셋: DL3DV (장면 10,015개)
- 카메라 포즈는 COLMAP으로 추정
1. Pose-Conditioned Feed-Forward 3DGS
저자들은 feed-forward novel view synthesis (FF-NVS)를 위하여 3DGS를 활용하였다. 최소 모델링 전략을 고수하며, 픽셀 정렬된 3D Gaussian을 추론하기 위해 DPT head (GS-DPT)를 추가하여 fine-tuning하는 방식으로 FF-NVS를 수행하였다.
GS-DPT head
Transformer backbone을 통해 추출된 각 뷰에 대한 비주얼 토큰이 주어지면, GS-DPT는 카메라 공간에서의 3D Gaussian 파라미터 \(\{\sigma_i, \textbf{q}_i, \textbf{s}_i, \textbf{c}_i\}_{i=1}^{H \times W}\)를 예측한다. 이 중 \(\sigma_i\)는 confidence head에서 예측하고 다른 것은 메인 GS-DPT head에서 예측한다. 추정된 깊이를 월드 프레임에 unprojection하여 3D Gaussian의 위치 \(\textbf{P}_i \in \mathbb{R}^3\)을 얻는다. 그런 다음, 주어진 카메라 포즈에서 새로운 뷰를 합성하기 위해 rasterizion된다.
학습 loss
NVS 모델은 렌더링된 새로운 뷰에 대한 photometric loss, 즉 \(\mathcal{L}_\textrm{MSE}\), \(\mathcal{L}_\textrm{LPIPS}\)와 관찰된 뷰의 추정 깊이에 대한 scale-shift-invariant depth loss \(\mathcal{L}_D\)로 fine-tuning되며 teacher–student 학습 패러다임을 따른다.
2. Pose-Adaptive Feed-Forward 3DGS
저자들은 벤치마크를 위한 포즈 조건부 버전에 더해, 실제 환경에서의 평가에 더 적합한 대안을 제시하였다. 이 버전은 동일한 사전 학습된 가중치를 사용하여 DA3와 완벽하게 통합되도록 설계되었으며, 카메라 포즈 유무에 관계없이 다양한 해상도와 입력 뷰 수에 걸쳐 novel view synthesis를 가능하게 한다.
포즈 적응형 설계
저자들은 모든 입력 이미지가 calibration되지 않았다고 가정하는 대신, 포즈가 있는 입력과 포즈가 없는 입력을 모두 수용하는 포즈 적응형 설계를 채택하였다. 이를 위해서는 두 가지 설계 선택이 필요하다.
- 모든 3DGS 파라미터는 로컬 카메라 공간에서 예측된다.
- Backbone은 포즈가 있는 이미지와 포즈가 없는 이미지를 매끄럽게 처리해야 한다.
DA3 backbone은 두 가지 요구 사항을 모두 충족한다. 포즈를 사용할 수 있는 경우, 예측된 깊이 및 카메라 공간 3DGS를 월드 공간으로 scaling하고 unprojection하여 포즈와 일치시킨다. 포즈를 사용할 수 없는 경우, 예측된 포즈를 월드 공간으로 unprojection하는 데 직접 사용한다.
정확한 표면 geometry와 렌더링 품질 간의 trade-off를 줄이기 위해 GS-DPT head에서 추가적인 depth offset을 예측한다. 실제 환경에서의 robustness를 높이기 위해, 3D Gaussian 색상을 spherical harmonic 계수로 대체하여 view-dependent한 표면 모델링을 통해 geometry와의 충돌을 줄였다.
향상된 학습 전략
불안정한 학습을 방지하기 위해 사전 학습된 가중치를 사용하여 DA3 backbone을 초기화하고 고정한 후, GS-DPT head만 튜닝한다. 실제 환경에서의 성능을 향상시키기 위해 다양한 이미지 해상도와 다양한 컨텍스트 뷰 개수를 사용하여 학습시켰다. 특히, 고해상도 입력에는 더 적은 컨텍스트 뷰를, 저해상도 입력에는 더 많은 뷰를 사용하여 학습을 안정화하는 동시에 다양한 평가 시나리오를 지원하였다.
Experiments
1. Comparison with State of the Art
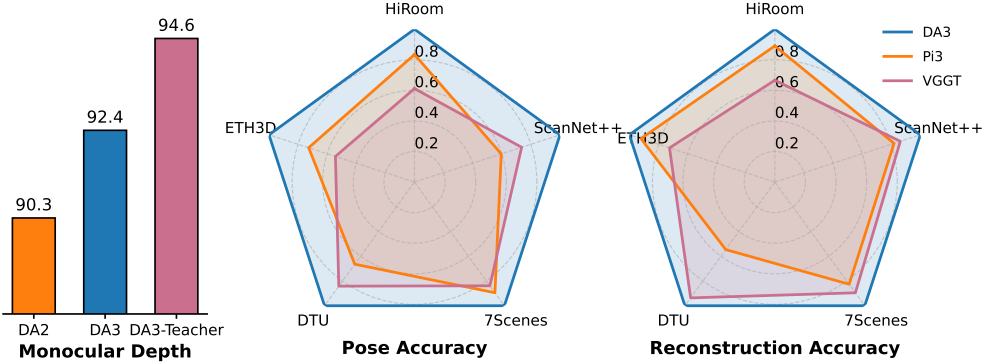
다음은 포즈 추정 품질을 비교한 결과이다.
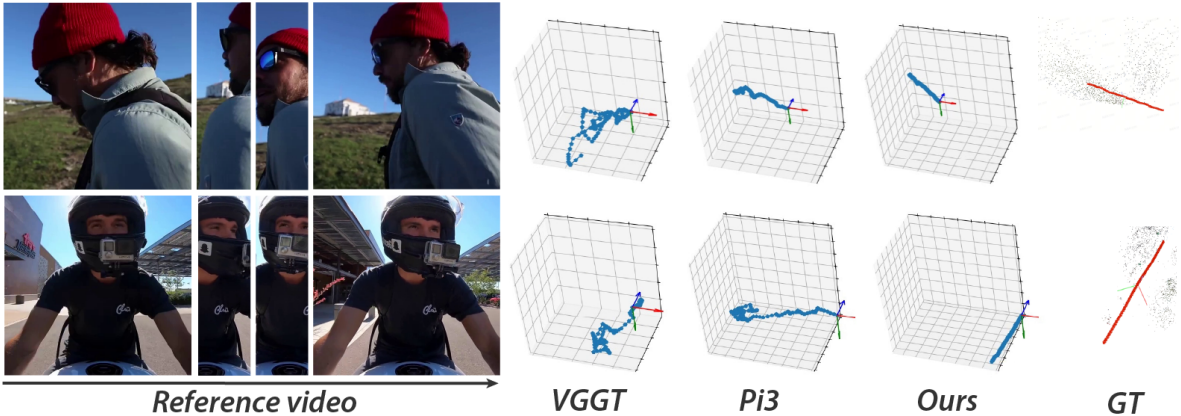
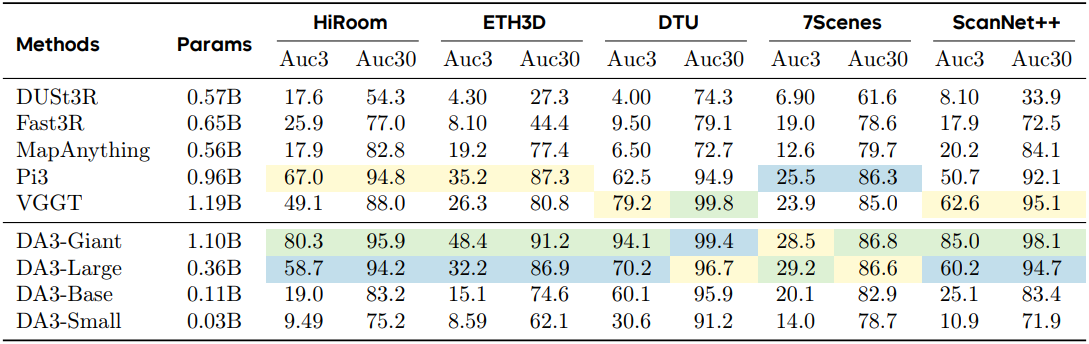
다음은 포인트 클라우드 품질을 비교한 결과이다. (DTU는 chamfer distance (mm), 나머지는 F1 score)

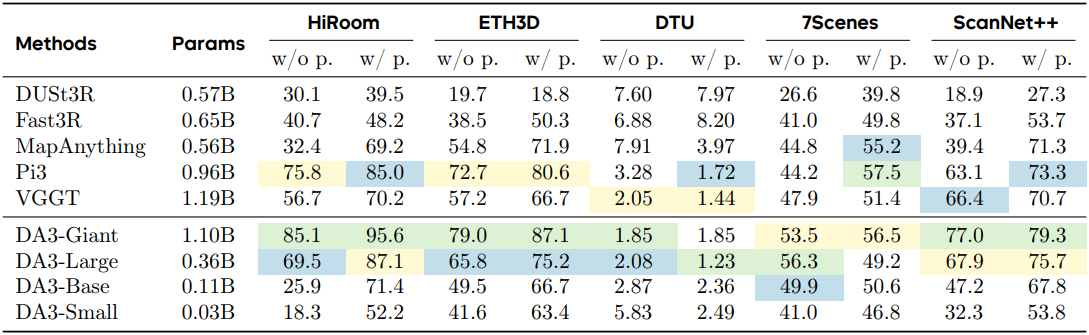
다음은 깊이 품질을 비교한 결과이다. (표는 monocular depth, \(\delta_1\))
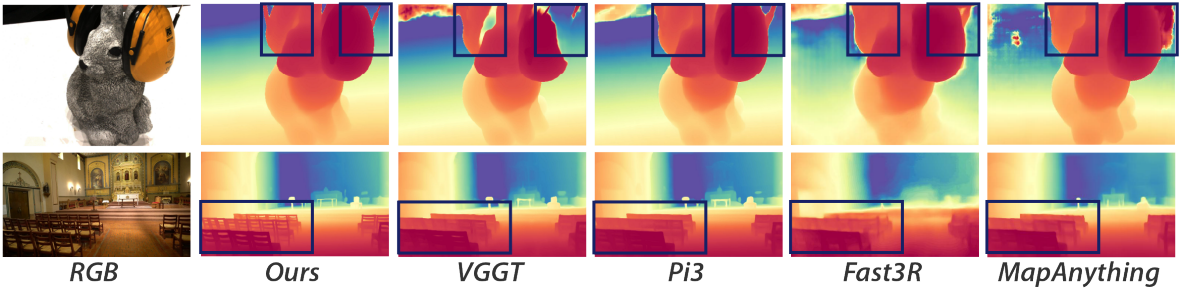
2. Analysis for Depth Anything 3
다음은 예측 타겟에 대한 ablation 결과이다.

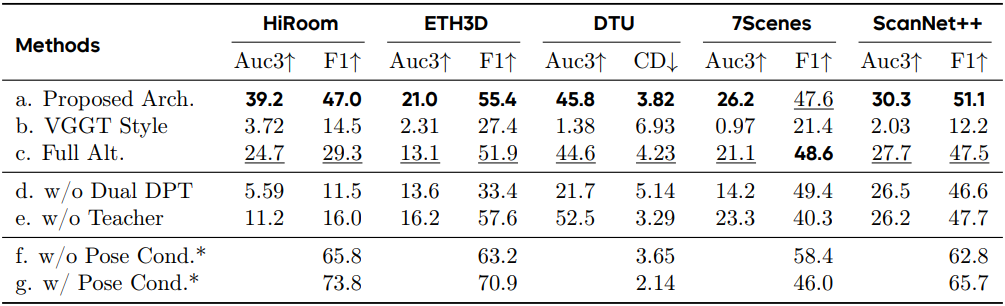
다음은 모델 아키텍처, Dual-DPT head, teacher 레이블, 포즈 컨디셔닝 모듈에 대한 ablation 결과이다.
다음은 teacher 레이블에 대한 ablation 결과를 시각적으로 비교한 것이다.

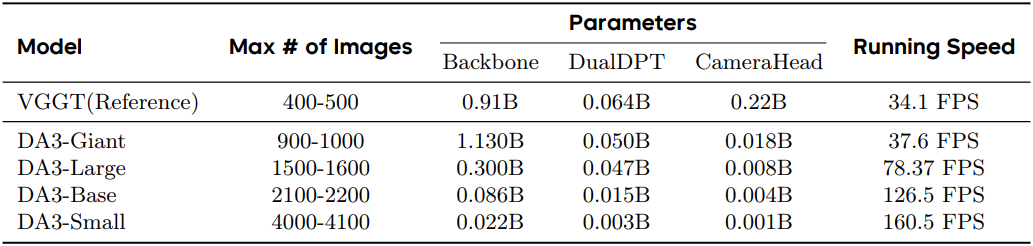
다음은 모델들의 파라미터 수와 속도를 비교한 결과이다.
3. Analysis for Depth-Anything-3-Monocular
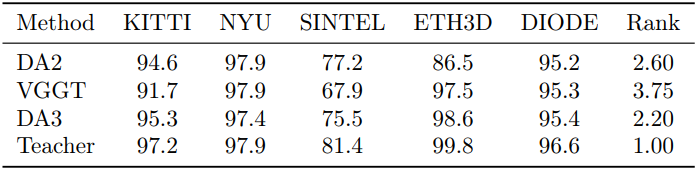
다음은 teacher 모델에 대한 ablation 결과이다.

다음은 monocular student의 DA2와 비교한 결과이다.

4. Analysis for Depth-Anything-3-Metric
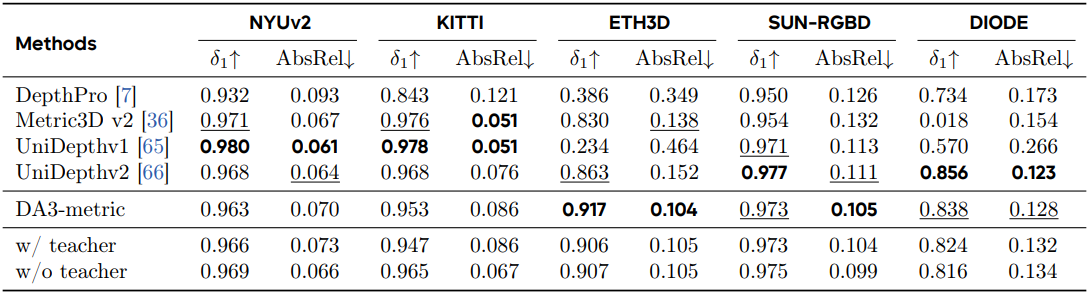
다음은 metric depth estimation에 대한 비교 결과이다.

5. Analysis for Feed-forward 3DGS
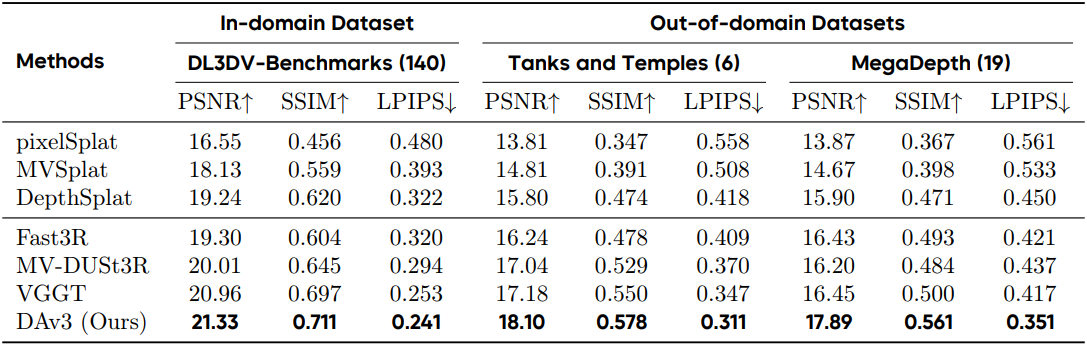
다음은 novel view synthesis에 대한 비교 결과이다.