[논문리뷰] Can We Achieve Efficient Diffusion without Self-Attention? Distilling Self-Attention into Convolutions

ICCV 2025. [Paper]
ZiYi Dong, Chengxing Zhou, Weijian Deng, Pengxu Wei, Xiangyang Ji, Liang Lin
Sun Yat-sen Unviersity | Australian National University | Peng Cheng Laboratory | Tsinghua University
30 Apr 2025

Introduction

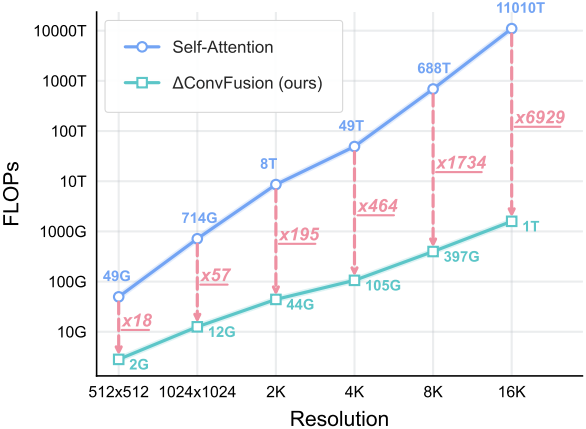
Diffusion model은 특히 고해상도 이미지 생성에서 제곱에 비례하는 계산 복잡도를 보이는 self-attention에 크게 의존한다. 최근에는 이러한 문제를 완화하기 위한 노력이 이루어지고 있지만, 글로벌한 공간적 상호작용의 필요성에 대한 근본적인 가정에 기반하고 있어, 효율성 개선이 최적화되지 못하고 메모리 효율성이 지속적으로 저하되는 한계를 가지고 있다.

본 논문에서는 다음과 같은 두 가지 핵심 질문을 고찰하였다.

1. Diffusion model에서 self-attention은 주로 글로벌 의존성을 포착하는가, 아니면 로컬 의존성에 더 중점을 두는가?
2. Self-attention의 장점을 유지하면서 self-attention 연산을 구조화된 convolution 방식으로 효과적으로 대체할 수 있는가?

저자들은 기존 DiT 및 U-Net 기반 diffusion 프레임워크에서 self-attention 특성을 체계적으로 조사했다. 먼저, 각 픽셀이 주로 공간적으로 인접한 픽셀들과 상호작용하여 convolution 연산과 유사한 구조화된 패턴을 형성하는 것을 관찰했다. 이를 토대로 self-attention map에 대한 정량적 분석을 수행했다. 분석 결과, 이론적으로 글로벌한 상호작용이 가능함에도 불구하고 self-attention은 주로 로컬 패턴을 나타내는 것으로 밝혀졌다. 이러한 점을 고려하여, self-attention map을 두 가지 핵심 요소로 분해했다.

1. 거리 의존적 고주파 성분: Query 픽셀로부터의 거리가 증가함에 따라 self-attention 강도가 제곱으로 감소하여 로컬성을 강화한다.
2. 저주파 성분: Self-attention map 전체에 걸쳐 공간적으로 불변하는 편향을 도입하여 넓고 공간적으로 부드러운 self-attention 분포에 기여한다.

이러한 통찰력을 바탕으로, 저자들은 self-attention 메커니즘을 Pyramid Convolution Blocks (∆ConvBlocks)으로 대체하는 새로운 CNN 기반 아키텍처인 ∆ConvFusion을 제안하였다. ∆ConvFusion은 multi-scale convolution을 활용하여 시각적 feature를 효율적으로 처리하는 동시에 diffusion model에서 관찰되는 attention 패턴을 재현한다. Self-attention 메커니즘의 두 가지 핵심 요소와 일치하도록, ∆ConvBlocks는 거리 의존적 고주파 성분을 포착하는 pyramid convolution 구조와 저주파 성분을 근사하는 average pooling branch를 포함한다. 이를 통해 ∆ConvBlocks는 self-attention map의 공간적 특성을 효과적으로 재현할 수 있다.

∆ConvFusion은 diffusion model의 self-attention 블록을 ∆ConvBlocks로 대체하여 구축한다. 효율적인 학습을 위해, 다른 모든 구성 요소는 고정하고 ∆ConvBlocks만 업데이트한다. 또한 저자들은 두 가지 레벨에서 knowledge distillation를 적용하였다.

1. Feature 레벨에서는 모든 layer에 걸쳐 ∆ConvBlocks와 원래의 self-attention 모듈 간의 불일치를 최소화한다.
2. 출력 레벨에서는 $\epsilon$-prediction objective를 사용하여 모델의 최종 출력을 정렬한다.

기존 방법들과 비교했을 때, ∆ConvFusion은 생성 성능을 유지하면서 계산 복잡도(FLOPs)와 GPU 메모리 사용량을 크게 줄인다.

Revisit Self-Attention in Diffusion Models

본 논문에서는 self-attention에서 글로벌한 상호작용의 역할을 조사하고 diffusion model에서 그 중요성을 평가하였다. 이를 위해 DiT와 U-Net 아키텍처 패러다임 모두에서 attention 패턴을 체계적으로 분석하였다. 또한, 주파수 영역에서 self-attention의 행동을 정량적으로 특성화하고 Effective Receptive Field (ERF)를 통해 로컬 패턴을 검증하였다.

1. Visual Analysis on Self-Attention

저자들은 self-attention 메커니즘의 attention map을 분석하여 공간적 패턴을 직관적으로 살펴보았다. $t$번째 timestep과 $l$번째 layer에서의 latent \(\textbf{z}_t^l \in \mathbb{R}^{H^\prime \times W^\prime \times C^\prime}\)에 대하여, self-attention map은 query 표현 \(\psi_q (\textbf{z}_t^l)\)과 key 표현 \(\psi_k (\textbf{z}_t^l)\) 사이의 유사도 점수로 계산된다.

\[\begin{equation} \textbf{A}_t^l = \textrm{Softmax} \left( \frac{\psi_q (\textbf{z}_t^l)^\top \psi_k (\textbf{z}_t^l)}{\sqrt{C_k}} \right) \end{equation}\]

\(\textbf{A}_t^l\)의 shape은 $(H^\prime W^\prime, H^\prime W^\prime)$이며, 시각화를 위해 $(H^\prime W^\prime, H^\prime, W^\prime)$로 reshape할 수 있다.

위 그림은 DiT 및 U-Net 아키텍처에서 전체 timestep에 대하여 집계된 평균 self-attention map \(\textbf{A}^l\)을 시각화한 것이다. 거의 모든 픽셀이 주변 영역에 고도로 집중된 attention 분포를 보이는 것을 확인할 수 있다.

2. Frequency Analysis on Self-Attention

저자들은 주파수 도메인에서 self-attention에 대한 정량적 패턴을 분석하였다. $l$번째 layer에 대하여, $\textbf{A}^l (x_i, y_j)(x_m, y_n)$은 self-attention map에서 $(x_i, y_j)$의 쿼리와 $(x_m, y_n)$의 픽셀 사이의 attention 점수이며, 다음 조건을 만족한다.

\[\begin{equation} \sum_{m=0}^{H^\prime} \sum_{n=0}^{W^\prime} \textbf{A}^l (x_i, y_j)(x_m, y_n) = 1 \end{equation}\]

Self-attention 분포를 측정하기 위해, 커널 크기가 $K$인 커널 영역에서 attention score mass (ASM)을 정의한다. 이 커널은 $(x_i, y_j)$를 중심으로 하는 $K \times K$ 커널이다.

\[\begin{equation} \textrm{ASM}^l (x_i, y_j) = \sum_{(x_m, y_n) \in d_\infty < \frac{K}{2}} \textbf{A}^l (x_i, y_j) (x_m, y_n) \end{equation}\]

Self-attention map에 대한 전체 ASM을 얻기 위해 모든 공간적 위치와 layer에 걸쳐 \(\textrm{ASM}^l (x_i, y_j)\)을 집계한다.

\[\begin{equation} \textrm{ASM} = \sum_l \sum_{i=0}^{H^\prime} \sum_{j=0}^{W^\prime} \textrm{ASM}^l (x_i, y_j) \end{equation}\]

ASM의 기울기는 공간적 거리가 증가함에 따라 attention 점수가 감소하는 비율을 정량화한다.

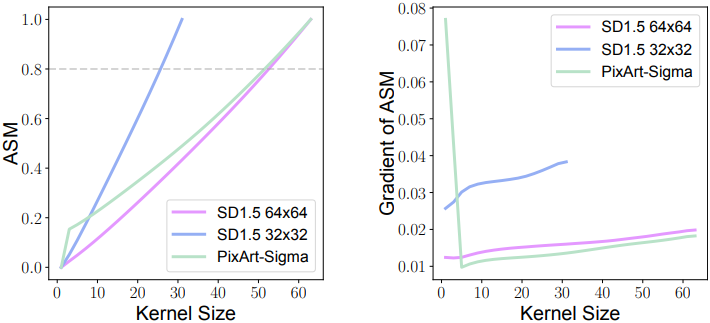
위 그림은 커널 크기 $K$에 따른 PixArt(DiT 아키텍처)와 SD1.5(U-Net 아키텍처)의 ASM을 나타낸 그래프이며, $K$와 ASM 사이에 일관된 이차 함수 관계를 보인다. 이는 attention이 주로 넓은 저주파 정보를 포착한다는 것을 나타낸다. 또한, ASM의 기울기가 작은 커널 크기에서 급격히 감소하고 큰 커널 크기에서 안정화되는 것을 보여주는데, 특히 SD1.5(32$\times$32)에서 이러한 경향이 두드러진다. 이는 대부분의 attention이 주변 영역에 집중되어 있음을 시사한다. $K$가 증가함에 따라 기울기는 꾸준히 0에 가까워지는데, 이는 receptive field를 특정 지점 이상으로 확장해도 ASM이 크게 변하지 않음을 나타낸다. 위의 분석은 self-attention이 이론적으로 글로벌 상호작용을 모델링할 수 있음에도 불구하고 주로 로컬하게 작동한다는 것을 확인시켜 준다.

저자들은 핵심 구조 정보를 담고 있는 고주파 성분의 역할을 더 자세히 조사하기 위해, 고주파 필터링 기법을 이용한 스펙트럼 분석을 수행하여 그 특성을 정량화하였다. 구체적으로, $(x_i, y_j)$에서의 쿼리에 대해 \(\textbf{A}^l (x_i, y_j)\)의 shape은 $(H^\prime, W^\prime)$이고, 이는 2차원 공간 신호로 간주할 수 있다. 스펙트럼 특성을 분석하기 위해 이산 푸리에 변환(DFT)을 적용한 후, 저주파 성분을 억제하기 위해 high-pass Butterworth filter를 사용하여 고주파 attention map \(\Lambda^l\)을 얻는다. 그런 다음, \(\Lambda^l\)에 대해 \(\textrm{ASM}_\Lambda^l\)을 다시 계산하여 고주파 성분의 기여도를 정량화할 수 있다.

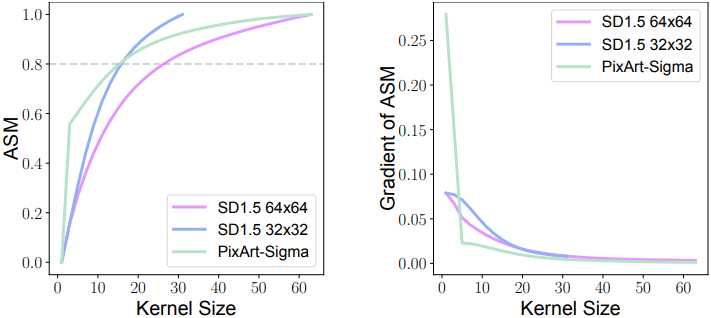
위 그림에서 볼 수 있듯이, 필터링된 attention map의 ASM과 기울기는 대부분의 중요한 attention이 작은 지역 내에 집중되어 있으며, 기울기는 거리가 증가함에 따라 제곱에 비례하여 감소함을 보여준다. 특히 PixArt에서는 고주파 attention 신호의 80% 이상이 10$\times$10 영역 내에 포착되는데, 이는 학습된 diffusion model에서 self-attention이 장거리 상호작용에 크게 기여하지 않음을 시사한다.

3. Effective Receptive Field Analysis on Self-Attention

Effective Receptive Field (ERF)는 효과적인 상호작용 영역을 측정하는 척도로서, self-attention의 대안으로 적절한 convolution 커널 크기를 설계하는 데 도움을 준다. 저자들은 $l$번째 self-attention의 ERF \(\hat{k}^l\)을 ASM의 최소 80%를 포함하는 \(\Lambda^l\) 상의 가장 작은 커널 크기로 정의하였다.

\[\begin{equation} \hat{k}^l = \min \left\{ k \in \{0, \ldots, K\} \vert \textrm{ASM}_\Lambda^l \ge 0.8 \right\} \end{equation}\]

위 그림에서 볼 수 있듯이, DiT 모델(PixArt)은 대부분의 layer에서 15$\times$15보다 작은 ERF를 나타내고, U-Net 모델(SD1.5)은 대부분의 layer에서 20$\times$20보다 작은 ERF를 나타낸다. 특히, 일부 transformer block에서 관찰되는 더 큰 receptive field는 attention map의 아티팩트에서 비롯된다. 이러한 transformer block의 self-attention은 마지막 픽셀에 비정상적으로 집중되어 있다.

이러한 현상에도 불구하고, 유효 attention은 쿼리 픽셀 주변에 집중되어 로컬한 공간 패턴을 나타낸다. 이는 현재의 diffusion model이 강한 로컬성을 보이며, 성능이 self-attention의 글로벌 모델링 능력에서 비롯되는 것이 아님을 시사한다.

4. Ablating Global Attention

저자들은 Neighborhood Attention (NA)을 사용하여 diffusion model에서 global self-attention을 제거했을 때의 영향을 체계적으로 조사하였다.

NA에서는 좌표 $(x_i, y_j)$에 위치한 특정 픽셀의 query에 대한 key와 value가 $(x_i, y_j)$을 중심으로 하는 $K \times K$ 크기의 로컬 window 내로 엄격하게 제한된다. 기존의 convolution layer와 유사하게, NA는 로컬 패턴과 receptive field 특성을 나타내므로 global self-attention 메커니즘의 대안으로 적합하다.

위 그림에서 볼 수 있듯이, SD 모델의 모든 self-attention layer를 NA($K = 13$)로 대체해도 semantic하게 일관성 있고 시각적으로 고품질의 이미지를 생성하는 모델의 능력은 유지된다. 이는 diffusion model에서 self-attention이 학습 과정에서 주로 로컬 패턴에 의존하기 때문에 모든 block에서 글로벌한 상호 작용이 필요하지 않을 수 있음을 시사한다. 그러나 NA는 여전히 높은 계산 오버헤드를 가지며 메모리 효율성이 떨어진다.

∆ConvFusion

위의 결과들은 diffusion model에서 self-attention이 주로 로컬한 방식으로 작동함을 보여주며, 이는 필수적인 공간적 상호작용을 보존하면서 계산 복잡도를 크게 줄이는 보다 효율적인 아키텍처의 가능성을 뒷받침한다. 이러한 통찰력을 바탕으로, 본 논문에서는 diffusion model에서 self-attention의 핵심 속성을 효과적으로 포착하는 구조화된 convolution 디자인인 ∆ConvBlock을 제안하였다. 구체적으로, ∆ConvBlock은 self-attention의 두 가지 핵심 요소와 일치하도록 설계되었다.

1. 거리 의존적 고주파 성분: 거리에 따라 attention 강도가 제곱으로 감소하여 강한 로컬성을 나타냄
2. 저주파 성분: Attention map 전체에 걸쳐 공간적으로 불변하는 편향을 도입함

1. Pyramid Convolution for Localized Interaction

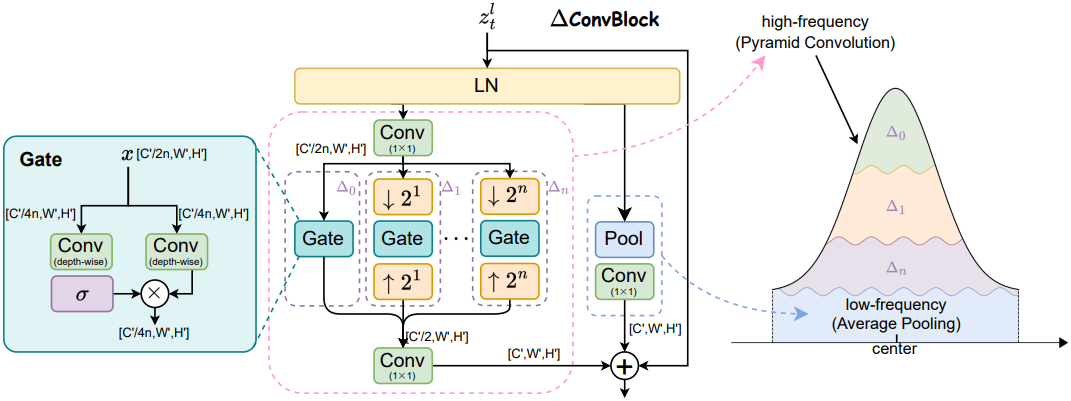
거리 의존적 고주파 성분을 포착하기 위해 ∆ConvBlock은 여러 피라미드 단계를 포함하는 pyramid convolution 구조를 통합한다. 구체적으로, 입력 latent feature map \(\textbf{z}_t^l \in \mathbb{R}^{H^\prime \times W^\prime \times C^\prime}\)에 대해, 먼저 Layer Normalization (LN)을 적용하여 정규화된 feature 표현 \(\tilde{\textbf{z}}_t^l\)을 얻는다. 그런 다음, 1$\times$1 convolution layer를 적용하여 채널 차원을 축소하고 계산 효율성을 높여 채널 간 상호 작용을 용이하게 한다.

\[\begin{equation} \tilde{\textbf{z}}_t^l = \textrm{LN}(\textbf{z}_t^l) \in \mathbb{R}^{H^\prime \times W^\prime \times C^\prime} \\ \textbf{z}_{t, \textrm{in}}^l = \psi_\textrm{in} (\tilde{\textbf{z}}_t^l) \in \mathbb{R}^{H^\prime \times W^\prime \times C^\prime / 2n} \end{equation}\]

($n$은 피라미드 단계 개수)

이후, 압축된 feature \(\textbf{z}_{t, \textrm{in}}^l\)은 여러 피라미드 단계를 거쳐 처리되어 다양한 스케일에 걸쳐 계층적 공간 상호 작용을 가능하게 한다. $i$번째 피라미드 단계 \(\Delta_i\)는 다양한 scaling factor를 갖는 업샘플링($\uparrow$) 및 다운샘플링($\downarrow$) 연산을 포함하여 다양한 receptive field를 달성하고 feature 표현을 향상시킨다.

피라미드 단계에서 비선형 공간 상호작용을 가능하게 하기 위해 depth-wise convolution을 사용하는 scaling된 단순 게이트 $\rho(\cdot)$를 사용한다. 기존의 단순 게이트는 element-wise multiplication을 사용하기 때문에, FP16 정밀도에서 필연적으로 오버플로를 발생시켜 학습 불안정성을 초래한다. 저자들은 이를 완화하기 위해, 다음과 같은 단순 게이트 $\rho (\textbf{f})$를 도입하였다.

\[\begin{equation} \rho (\textbf{f}) = \frac{\textbf{f}_{< C^\prime / 2} \cdot \textbf{f}_{\ge C^\prime / 2}}{\sqrt{C^\prime}} \end{equation}\]

($C^\prime$은 입력 feature $\textbf{f}$의 채널 수)

이 아키텍처에서는 중심에 가까운 픽셀일수록 더 많은 피라미드 단계를 거치므로 더 높은 가중치를 축적한다. 이러한 특징은 고주파 성분의 특성과 일치한다. ∆ConvBlock은 멀티스케일 공간 상호작용을 위해 선형적인 계산 복잡도를 갖는 연산을 활용하여 낮은 계산 오버헤드를 유지하면서 로컬 디테일 보존과 글로벌 공간 인식을 동시에 향상시킨다.

\[\begin{equation} \Delta_\theta^l = \sum_{i=1}^n \Delta_i (\textbf{z}_{t, \textrm{in}}^l) = \sum_{i=1}^n (\uparrow 2^i (\rho (\downarrow 2^i (\textbf{z}_{t, \textrm{in}}^l)))) \end{equation}\]

($\downarrow 2^i$는 다운샘플링 scale이 $2^i$인 average pooling layer, $\uparrow 2^i$는 업샘플링 scale이 $2^i$인 bilinear interpolation)

마지막으로 1$\times$1 convolution layer을 적용한다.

2. Average Pooling as Attention Bias

∆ConvBlock의 두 번째 구성 요소는 저주파 성분을 포착하는 average pooling branch이다. 이는 1$\times$1 average pooling layer와 그 뒤에 오는 1$\times$1 convolution layer \(\psi_p\)로 구성된다\dots

\[\begin{equation} \textbf{f}_\textrm{out}^\textrm{avg} = \psi_p \left( \frac{1}{HW} \sum_x^W \sum_y^H \tilde{\textbf{z}}_t^l (x, y) \right) \end{equation}\]

1$\times$1 convolution과 average pooling의 선형성을 고려할 때, 이 연산은 다음 등식을 만족한다.

\[\begin{equation} \psi_p \left( \frac{1}{HW} \sum_x^W \sum_y^H \tilde{\textbf{z}}_t^l (x, y) \right) = \frac{1}{HW} \sum_x^W \sum_y^H \psi_p (\tilde{\textbf{z}}_t^l (x, y)) \end{equation}\]

Average pooling 전과 후에 적용된 1$\times$1 convolution은 서로 동등하다. 이러한 아키텍처 디자인은 낮은 계산 복잡도를 유지하면서 self-attention이 포착하는 저주파 정보를 효과적으로 보완한다.

3. Efficient Training via Distillation

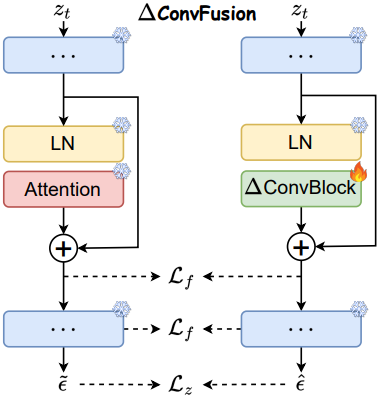
∆ConvBlocks가 관찰된 로컬성을 유지하면서 diffusion model에서 self-attention 모듈을 효과적으로 대체할 수 있도록, ∆ConvBlocks만 업데이트하고 다른 모든 파라미터는 고정한다. 또한, self-attention 패턴을 ∆ConvBlocks로 전송하기 위해 knowledge distillation을 적용하여 feature 레벨과 출력 레벨 모두에서 정렬을 보장한다.

Feature 레벨 정렬의 경우, 모든 layer에 걸쳐 ∆ConvBlock과 원래 self-attention 모듈의 출력 간의 차이 \(\mathcal{L}_f\)를 최소화한다.

\[\begin{equation} \mathcal{L}_f = \sum_{l=1}^N \| \Delta_\theta^l (\textbf{z}_t^l) - \textbf{z}_{t, \textrm{out}}^l \|^2 \end{equation}\]

(\(\textbf{z}_{t, \textrm{out}}^l\)은 원래 self-attention block의 출력)

출력 레벨 정렬의 경우, $\epsilon$-prediction objective를 사용한다. 수렴 속도를 더욱 높이기 위해 출력 예측 \(\mathcal{L}_z\)에 대한 loss는 Min-SNR loss weighting을 통해 개선된다.

\[\begin{equation} \mathcal{L}_z = \min (\gamma \cdot (\sigma_t^z / \sigma_t^\epsilon)^2, 1) \cdot (\| \tilde{\epsilon} - \hat{\epsilon} ) \end{equation}\]

(\(\tilde{\epsilon}\)은 원래 self-attention 기반 모델의 출력, \(\hat{\epsilon}\)은 ∆ConvFusion 모델의 출력)

최종 loss function은 다음과 같다.

\[\begin{equation} \mathcal{L} = \mathcal{L}_z + \beta \mathcal{L}_f \end{equation}\]

Experiments

1. Computational Complexity and Latency

다음은 inference를 위한 평균 계산 비용을 비교한 결과이다.

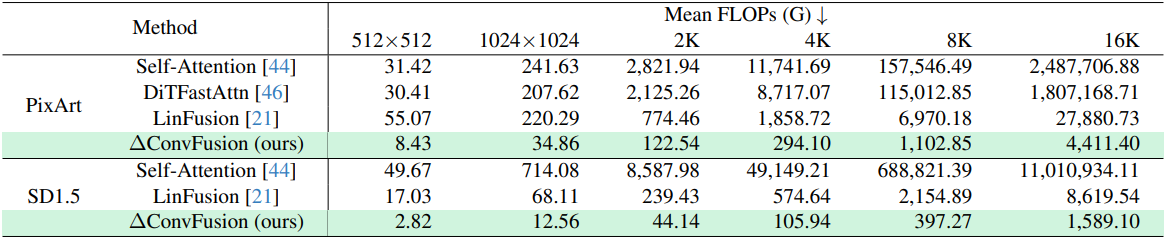
다음은 평균 inference 속도를 비교한 결과이다.

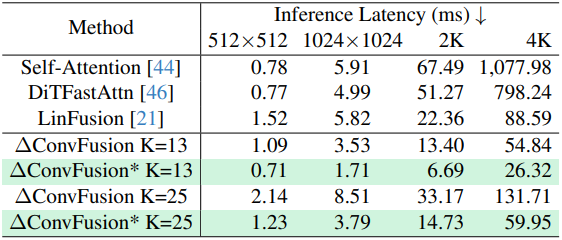
2. Evaluation

다음은 ∆ConvFusion과 다른 방법들의 이미지 생성 성능을 비교한 결과이다.

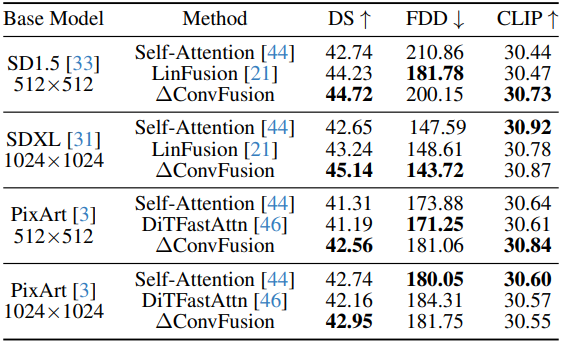
3. Model Analysis

다음은 ∆ConvFusion과 self-attention 기반 모델의 ERF를 시각화한 것이다.