[논문리뷰] Deblurring 3D Gaussian Splatting
arXiv 2024. [Paper] [Page]
Byeonghyeon Lee, Howoong Lee, Xiangyu Sun, Usman Ali, Eunbyung Park
Sungkyunkwan University | Hanhwa Vision
1 Jan 2024
Introduction
최근 3D Gaussian Splatting (3D-GS)는 매우 빠른 렌더링 속도로 고품질 이미지를 생성하는 능력을 입증하면서 큰 주목을 받았다. NeRF의 시간이 많이 걸리는 볼륨 렌더링을 대체하여 미분 가능한 splatting 기반 rasterization으로 3D 장면을 표현하기 위해 수많은 컬러 3D Gaussian을 결합한다. 렌더링 프로세스에서는 3D Gaussian point들을 2D 이미지 평면에 투영되며 이러한 가Gaussian들의 위치, 크기, 회전, 색상, 불투명도는 기울기 기반 최적화를 통해 조정되어 3D 장면을 더 잘 캡처한다. 3D-GS는 최신 그래픽 하드웨어의 볼륨 렌더링 기술보다 훨씬 효율적일 수 있는 rasterization을 활용하므로 신속한 실시간 렌더링이 가능하다.
본 연구에서는 rasterization과 잘 정렬되어 실시간 렌더링이 가능한 3D-GS용 최초의 defocus deblurring 알고리즘인 Deblurring 3D-GS를 제안하였다. 이를 위해 3D Gaussian의 공분산 행렬을 수정하여 흐릿함을 모델링한다. 구체적으로 각 3D Gaussian의 공분산을 조작하여 장면 흐림을 모델링하는 작은 MLP를 사용한다. 흐릿함은 인접한 픽셀의 혼합을 기반으로 하는 현상이므로 Deblurring 3D-GS는 학습하는 동안 이러한 혼합을 시뮬레이션한다. 이를 위해 저자들은 MLP를 활용하여 3D Gaussian의 다양한 속성 변화를 학습하는 프레임워크를 설계했다. 이러한 작은 변형은 속성의 원래 값에 곱해지며 결과적으로 Gaussian의 업데이트된 모양이 결정된다. Inference 시에는 MLP 없이 3D-GS의 원래 구성 요소만 사용하여 장면을 렌더링한다. 따라서 3D-GS는 각 픽셀이 인근 픽셀과 섞이지 않기 때문에 선명한 이미지를 렌더링할 수 있다. 또한 inference 중에는 MLP가 활성화되지 않기 때문에 흐릿한 이미지에서 세밀하고 선명한 디테일을 재구성하면서 3D-GS와 유사한 실시간 렌더링이 가능하다.
3D-GS는 일반적으로 Structure-from-Motion (SfM)에서 얻은 sparse한 포인트 클라우드에서 3D 장면을 모델링한다. SfM은 멀티뷰 이미지에서 feature들을 추출하고 이를 장면의 3D 포인트를 통해 연결한다. 주어진 이미지가 흐릿하면 SfM은 유효한 feature를 식별하는 데 크게 실패하고 결국 매우 적은 수의 포인트를 추출하게 된다. 더 나쁜 것은 장면의 depth of field가 더 크다면 SfM은 장면의 맨 끝에 있는 점을 거의 추출하지 않는다는 것이다. 흐릿한 이미지들로 구성된 포인트 클라우드의 과도한 sparsity로 인해 포인트 클라우드에 의존하는 3DGS를 포함한 기존 방법은 장면을 세밀하게 재구성하지 못한다. 이러한 과도한 sparsity를 보상하기 위해 N-nearest-neighbor interpolation을 사용하여 포인트 클라우드에 유효한 색상 feature들을 가진 추가 포인트를 추가한다. 또한 먼 거리의 평면에 더 많은 Gaussian을 유지하기 위해 위치에 따라 Gaussian을 pruning한다.
Deblurring 3D-GS는 다양한 벤치마크에서 SOTA 렌더링 품질을 달성하거나 현재 주요 모델과 동등한 성능을 발휘하면서 훨씬 더 빠른 렌더링 속도(> 200FPS)를 달성하였다.
Deblurring 3D Gaussian Splatting
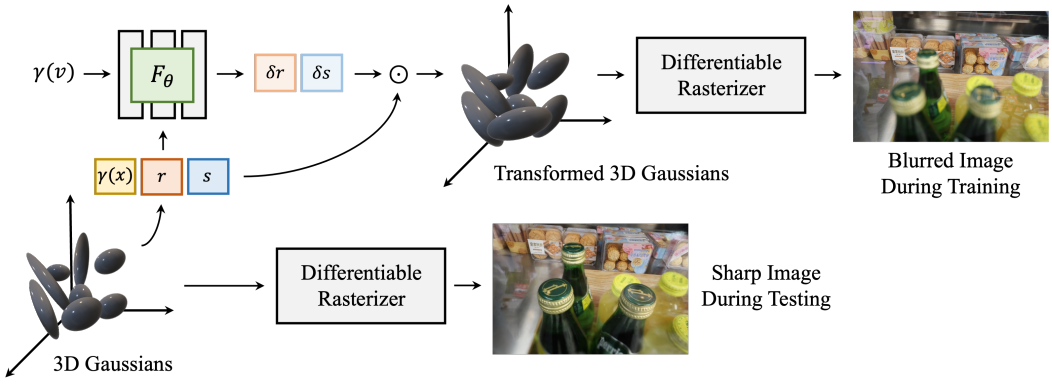
3D-GS를 기반으로 3D Gaussian들을 생성하고 각 Gaussian은 3D 위치 $x$, 불투명도 $\sigma$, quaternion $r$과 scale $s$로 계산되는 공분산 행렬을 포함한 파라미터 집합으로 고유하게 특성화된다. 각 3D Gaussian에는 뷰에 따른 모양을 나타내는 spherical harmonics(SH)도 포함되어 있다. 입력은 Structure-from-Motion(SfM)을 통해 얻을 수 있는 카메라 포즈와 포인트 클라우드, 그리고 이미지들의 컬렉션으로 구성된다. 3D Gaussian을 deblurring하기 위해 $r$과 $s$에 대한 3D Gaussian의 위치를 입력으로 받고 $\delta r$과 $\delta s$를 출력하는 MLP를 사용한다. 새로운 quaternion과 scale인 $r \cdot \delta r$과 $s \cdot \delta s$를 사용하면 업데이트된 3D Gaussian이 타일 기반 rasterizer에 공급되어 흐릿한 이미지를 생성한다. 이 방법의 개요는 위 그림에 나와 있다.
1. Differential Rendering via 3D Gaussian Splatting
학습 시, 흐릿한 이미지는 미분 가능한 방식으로 렌더링되며 deblurring 3D Gaussian들을 학습시키기 위해 기울기 기반 최적화를 사용한다. 저자들은 미분 가능한 rasterization을 제안하는 3D-GS의 방법을 채택하였다. 각 3D Gaussian은 다음과 같이 3D world space $x$의 평균값을 갖는 공분산 행렬 $\Sigma (r, s)$로 정의된다.
\[\begin{equation} G(x, r, s) = e^{-\frac{1}{2} x^\top \Sigma^{-1} (r, s) x} \end{equation}\]$\Sigma (r, s)$와 $x$ 외에도 3D Gaussian은 spherical harmonics(SH) 계수로 정의되어 알파 값에 대한 뷰에 따른 모양 및 불투명도를 나타낸다. 공분산 행렬은 positive semi-definite를 만족하는 경우에만 유효하며, 이는 최적화 중에 제한하기 어렵다. 따라서 공분산 행렬은 회전을 나타내는 quaternion $r$과 스케일링을 나타내는 $s$라는 두 개의 학습 가능한 성분으로 분해되어 positive semi-definite 제약 조건을 우회한다. $r$과 $s$는 각각 회전 행렬과 스케일링 행렬로 변환되어 다음과 같이 $\Sigma (r, s)$를 구성한다.
\[\begin{equation} \Sigma (r, s) = R(r) S(s) S(s)^\top R(r)^\top \end{equation}\]여기서 $R(r)$은 $r$의 회전 행렬이고 $S(s)$는 $s$의 스케일링 행렬이다. 이러한 3D Gaussian은 2D 공간에 투영되어 다음과 같은 2D 공분산 행렬 $\Sigma^\prime (r, s)$을 사용하여 2D 이미지를 렌더링한다.
\[\begin{equation} \Sigma^\prime (r, s) = JW \Sigma (r,s) W^\top J^\top \end{equation}\]여기서 $J$는 projective transformation의 affine 근사의 Jacobian을 나타내고, $W$는 world-to-camera matrix를 나타낸다. 각 픽셀 값은 다음 식을 사용하여 각 픽셀에 중첩된 $N$개의 투영된 2D Gaussian을 누적하여 계산된다.
\[\begin{equation} C = \sum_{i \in N} T_i c_i \alpha_i \quad \textrm{with} \quad T_i = \prod_{j=1}^{i-1} (1 - \alpha_j) \end{equation}\]$c_i$는 각 포인트의 색상이고 $T_i$는 투과율이다. $α_i \in [0, 1]$는 $1 − \exp(−\sigma_i \delta_i)$로 정의된다. 여기서 $\sigma_i$와 $\delta_i$는 각각 포인트의 밀도와 광선에서의 간격이다.
2. Deblurring 3D Gaussians
Motivation
Defocusing으로 인해 이미지의 픽셀이 흐려지는 현상은 일반적으로 convolution 연산을 통해 모델링된다. Thin lens law에 따르면 카메라의 초점 거리에 있는 장면 포인트가 이미지 평면에서 선명한 이미지를 만든다. 반면, 초점 거리에 있지 않은 장면 포인트는 이미지 평면에서 얼룩을 만들고 흐릿한 이미지를 생성한다. 장면 포인트의 초점 거리로부터의 분리가 크면 넓은 영역의 얼룩이 생성되며 이는 심각한 흐림에 해당한다. 이러한 흐림 효과는 일반적으로 point spread function(PSF)로 알려진 2D Gaussian 함수로 모델링된다. 이에 따라 카메라로 캡처한 이미지는 실제 이미지와 PSF의 convolution 결과이다. 인접 픽셀의 가중치 합산인 이 convolution을 통해 가중치에 따라 소수의 픽셀이 중앙 픽셀에 크게 영향을 미칠 수 있다. 즉, defocus imaging 과정에서 픽셀은 주변 픽셀의 강도에 영향을 미친다. 이 이론적 기반은 저자들에게 deblurring 3D Gaussian 프레임워크를 구축하려는 동기를 제공하였다. 저자들은 큰 크기의 3D Gaussian이 흐림을 유발하는 반면 상대적으로 작은 3D Gaussian은 선명한 이미지에 해당한다고 가정하였다. 이는 분산이 큰 것일수록 이미지 공간에서 더 넓은 영역을 담당하므로 더 많은 인접 정보의 영향을 받아 인접 픽셀의 간섭을 나타낼 수 있기 때문이다. 3D 장면의 미세한 디테일은 더 작은 3D Gaussian들을 통해 더 잘 모델링될 수 있다.
Modelling
위에서 언급한 동기에 따라 3D Gaussian의 형상을 변환하여 deblurring하는 방법을 학습한다. 3D Gaussian의 형상은 공분산 행렬을 통해 표현되며, 이는 앞서 언급한 rotation factor와 scaling factor로 분해될 수 있다. 따라서 블러링 현상을 모델링할 수 있는 방식으로 3D Gaussian의 rotation factor와 scaling factor를 변경하는 것이 목표이다. 이를 위해 다음과 같이 3D Gaussian의 위치 $x$, rotation $r$, scale $s$, 시야 방향 $v$를 입력으로 사용하고 $(\delta r, \delta s)$를 출력하는 MLP를 사용한다.
\[\begin{equation} (\delta r, \delta s) = \mathcal{F}_\theta (\gamma (x), r, s, \gamma (v)) \end{equation}\]여기서 \(\mathcal{F}_\theta\)는 MLP이고 $\gamma$는 다음과 같이 정의되는 위치 인코딩이다.
\[\begin{equation} \gamma (p) = (\sin (2^k \pi p), \cos (2^k \pi p))_{k=0}^{L-1} \end{equation}\]여기서 $L$은 주파수의 수이고 위치 인코딩은 벡터 $p$의 각 요소에 적용된다.
변환된 속성 $r^\prime = r \cdot \delta r$과 $s^\prime = s \cdot \delta s$를 얻기 위해 이러한 $(\delta r, \delta s)$의 최소값은 1로 clip되고 element-wise로 $r$과 $s$에 각각 곱해진다. 이러한 변환된 속성을 사용하여 변환된 3D Gaussian $G(x, r^\prime, s^\prime)$를 구성할 수 있으며, 이는 장면 블러링을 모델링하기 위해 학습 중에 최적화된다. $s^\prime$이 $s$보다 크거나 같으므로 $G(x, r^\prime, s^\prime)$의 각 3D Gaussian은 원래 3D Gaussian $G(x, r, s)$보다 더 큰 분산을 갖는다. 3D Gaussian의 확장된 분산을 통해 defocus blur의 근본 원인인 주변 정보의 간섭을 표현할 수 있다. 또한, $G(x, r^\prime, s^\prime)$는 Gaussian별 $\delta r$과 $\delta s$가 추정됨에 따라 흐릿한 장면을 보다 유연하게 모델링할 수 있다. Defocus blur는 공간적으로 다양하며, 이는 영역마다 흐린 수준이 다르다는 것을 의미한다. 넓은 범위의 다양한 주변 정보가 포함된 심한 defocus blur가 있는 영역을 담당하는 3D Gaussian의 scaling factor는 높은 수준의 블러링을 더 잘 모델링하기 위해 더 커진다. 반면에 sharp한 영역의 3D Gaussian에 대한 값은 1에 가까워 분산이 더 작고 주변 정보의 영향을 나타내지 않는다.
Inference 시 선명한 이미지를 렌더링하기 위해 $G(x, r, s)$를 사용한다. 앞서 언급했듯이, 저자들은 3D Gaussian의 형상을 변환하기 위해 두 가지 다른 scaling factor를 곱하는 것이 blur kernel과 convolution으로 작동할 수 있다고 가정하였다. 따라서 $G(x, r, s)$는 깨끗하고 세밀한 디테일의 이미지를 생성할 수 있다. 테스트 시 이미지를 렌더링하는 데 추가 scaling factor가 사용되지 않기 때문에 \(\mathcal{F}_\theta\)가 활성화되지 않으므로 Deblurring 3D-GS의 inference에 필요한 모든 단계가 3D-GS와 동일하므로 실시간 렌더링이 가능하다. 학습 측면에서 \(\mathcal{F}_\theta\) forwarding과 간단한 element-wise multiplication만 추가 비용이다.
Selective blurring
제안하는 방법은 장면의 다양한 부분에서 임의로 블러링된 학습 이미지를 처리할 수 있다. 각 Gaussian에 대해 $(\delta r, \delta_s)$를 예측하므로 학습 이미지의 일부가 흐려지는 Gaussian의 공분산을 선택적으로 확대할 수 있다. 이렇게 변환된 Gaussian당 공분산은 2D 공간에 투영되며 이미지 공간에서 픽셀 단위의 blur kernel 역할을 할 수 있다. 블러링은 공간적으로 다양하기 때문에 다양한 모양의 blur kernel을 다양한 픽셀에 적용하는 것이 장면 블러링을 모델링하는 데 중추적인 역할을 한다. 이러한 유연성을 통해 3D-GS에서 deblurring 능력을 효과적으로 구현할 수 있다.
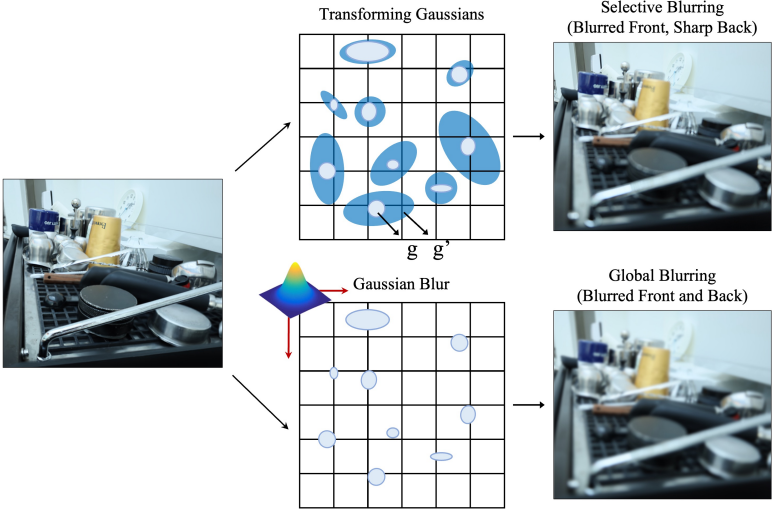
반면, 렌더링된 이미지를 흐리게 하는 간단한 접근 방식은 단순히 Gaussian kernel을 적용하는 것이다. 위 그림에서 볼 수 있듯이 이 접근 방식은 픽셀 단위로 흐리게 하지 않고 전체 이미지를 흐리게 하여 모델 학습을 위해 흐리게 해서는 안 되는 부분을 흐리게 만든다. 학습 가능한 Gaussian 커널을 적용하여 Gaussian kernel의 평균과 분산을 최적화하더라도 단일 유형의 blur kernel은 복잡하게 흐려진 장면을 모델링하기에는 표현력이 제한되고 loss function을 평균 내어 장면의 평균 블러링을 모델링하는 데 최적화된다. 이는 각 픽셀의 블러링을 모델링하지 못한다. 당연히 Gaussian blur는 제안된 방법의 특별한 경우이다. 모든 3D Gaussian에 대해 하나의 $\delta s$를 예측하면 유사하게 전체 이미지가 흐려진다.
3. Compensation for Sparse Point Cloud
3D-GS는 포인트 클라우드에서 여러 3D Gaussian을 구성하여 3D 장면을 모델링하며, 재구성 품질은 초기 포인트 클라우드에 크게 의존한다. 포인트 클라우드는 일반적으로 멀티뷰 이미지에서 feature들을 추출하고 이를 여러 3D 포인트와 연결하는 Structure-from-Motion(SfM)에서 얻는다. 그러나 흐릿한 입력에서 feature를 추출하는 문제로 인해 주어진 이미지가 흐릿한 경우 sparse한 포인트 클라우드만 생성할 수 있다. 더 나쁜 것은 depth of field가 큰 경우 SfM은 장면의 맨 끝에 있는 포인트를 거의 추출하지 않는다는 것이다.
Dense한 포인트 클라우드를 만들기 위해 $N_{st}$ iteration 후에 포인트를 추가한다. $N_p$개의 포인트는 균일 분포 $U(\alpha, \beta)$에서 샘플링된다. 여기서 $\alpha$와 $\beta$는 각각 기존 포인트 클라우드에서 포인트 위치의 최소값과 최대값이다. 각각의 새로운 점 $p$에 대한 색상은 K-Nearest-Neigbhor(KNN)을 사용하여 기존 점 중 가장 가까운 이웃 $P_\textrm{knn}$에서 보간된 색상 $p_c$로 할당된다. 빈 공간에 불필요한 포인트가 할당되는 것을 방지하기 위해 nearest neighbor까지의 거리가 distance threshold $t_d$를 초과하는 포인트를 폐기한다. 주어진 포인트 클라우드에 포인트를 추가하는 과정은 알고리즘 1에 요약되어 있다.

또한 3D-GS는 주기적인 적응형 밀도 제어, 3D Gaussian의 densifying과 pruning을 통해 3D Gaussian 수를 효과적으로 관리한다. 장면의 맨 끝에 있는 3D Gaussian의 sparsity를 보상하기 위해 위치에 따라 3D Gaussian을 pruning한다. 벤치마크 DeblurNeRF 데이터셋은 전방 장면으로만 구성되므로 각 지점의 $z$축 값은 모든 시점에서 상대적인 깊이가 될 수 있다.
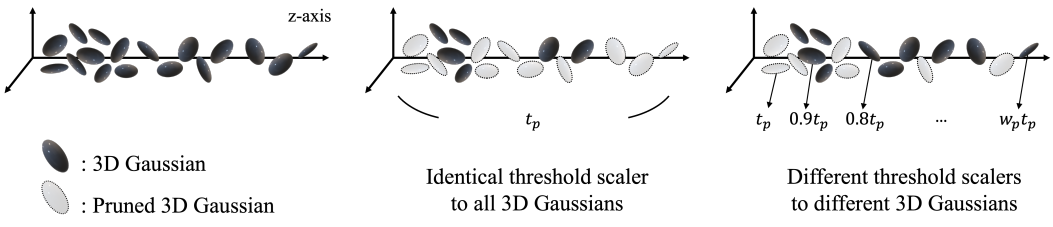
위 그림에서 볼 수 있듯이, 상대적 깊이에 의존하여 먼 평면에 있는 더 많은 점을 보존하기 위해 장면의 먼 가장자리에 배치된 더 적은 3D Gaussian을 pruning한다. 구체적으로, pruning threshold $t_p$는 상대적 깊이에 따라 $w_p$만큼 1.0으로 스케일링되며, 가장 먼 포인트에는 가장 낮은 threshold가 적용된다. 먼 거리의 평면에 있는 3D Gaussian에 대하여 densify하는 것도 사용 가능한 옵션이지만 과도한 보상은 장면 흐림 모델링을 방해하고 추가 계산 비용이 필요하므로 실시간 렌더링 성능을 더욱 저하시킬 수 있다. 저자들은 렌더링 속도를 고려할 때 유연한 pruning이 sparse한 포인트 클라우드를 보상하기에 충분하다는 것을 경험적으로 발견했다.
Experiments
- 구현 디테일
- optimizer: Adam (3D-GS와 동일한 세팅)
- iteration: 30,000
- MLP
- learning rate: $10^{-3}$
- hidden layer: 3
- hidden unit: 64
- activation: ReLU
- initialization: Xavier
- $N_{st} = 2,500$, $N_p = 100,000$
- neighbor의 수 $K$: 4
- $t_d = 10$, $t_p = 5 \times 10^{-3}$, $w_p = 0.3$
- GPU: NVIDIA RTX 4090 GPU (24GB)
1. Results and Comparisons
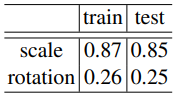
다음은 3D Gaussian의 rotation 및 scale 변환에 평균 값이다.
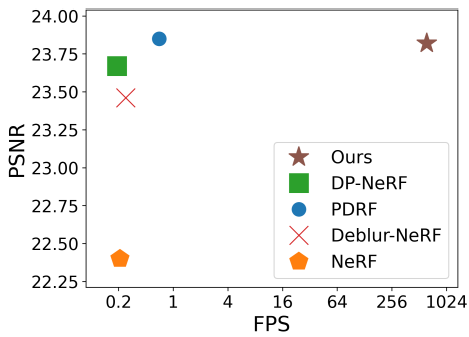
다음은 SOTA deblurring NeRF와 성능을 비교한 그래프이다.
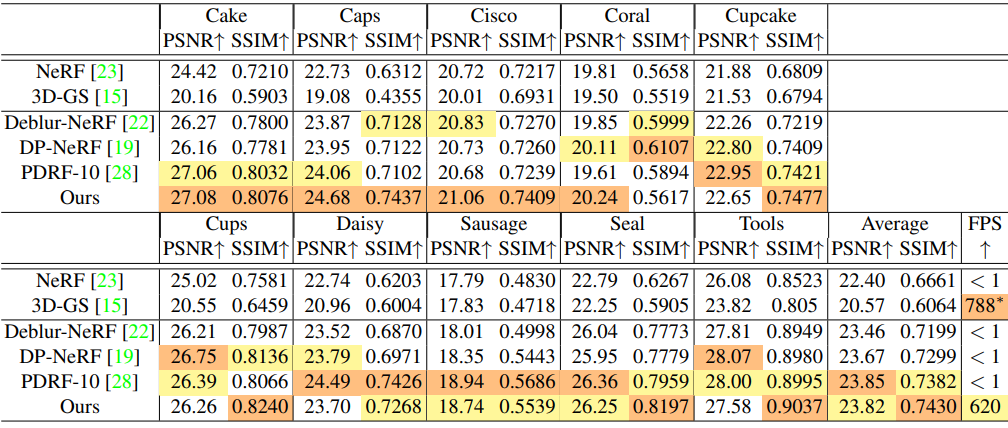
다음은 실제 defocus blur 데이터셋에 대한 결과를 비교한 것이다.
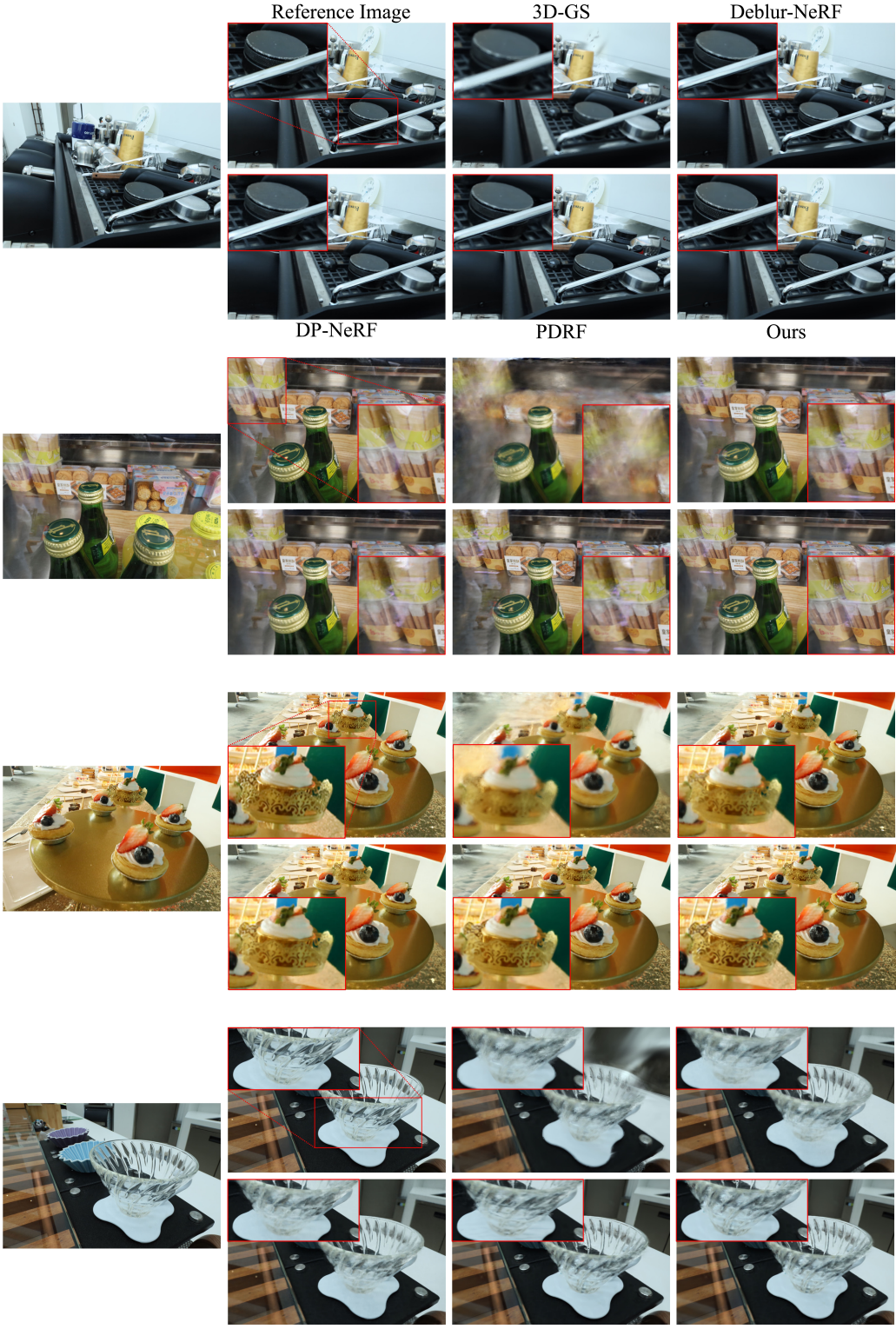
다음은 합성된 defocus blur 데이터셋에 대한 결과를 비교한 것이다.
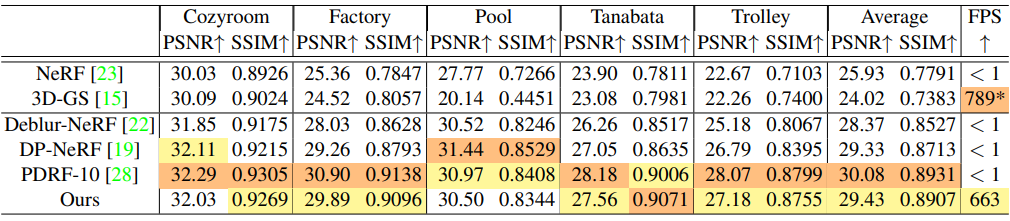

2. Ablation Study
Extra points allocation
다음은 학습 중에 포인트를 추가하지 않은 경우(중간)와 추가한 경우(오른쪽)을 비교한 것이다.

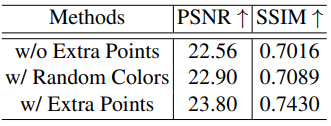
다음은 포인트 추가에 대한 ablation study 결과이다.
Depth-based pruning
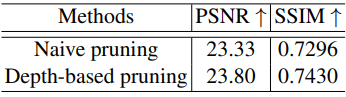
다음은 깊이 기반 pruning에 대한 ablation study 결과이다.
다음은 깊이 기반 pruning(왼쪽)과 3D-GS의 일반 pruning(오른쪽)을 비교한 것이다.
