[논문리뷰] DDSP: Differentiable Digital Signal Processing

ICLR 2020. [Paper] [Github]
Jesse Engel, Lamtharn Hantrakul, Chenjie Gu, Adam Roberts
Google Research, Brain Team
14 Jan 2020

Introduction

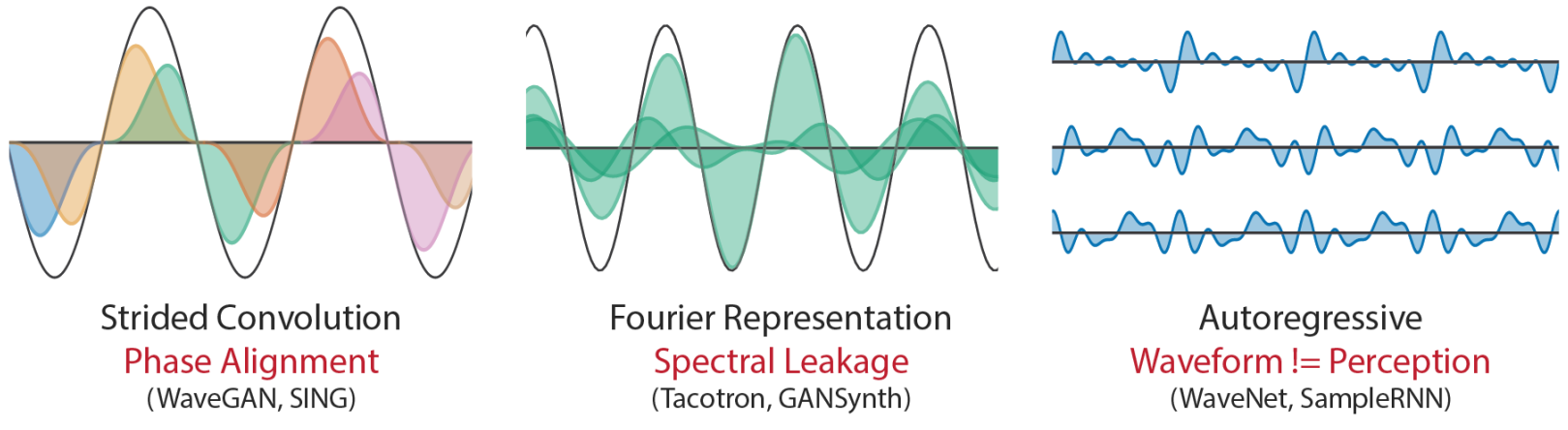
위 그림에서 볼 수 있듯이 대부분의 neural synthesis model은 시간 도메인에서 직접 waveform을 생성하거나 주파수 도메인에서 해당 푸리에 계수로부터 waveform을 생성한다. 이러한 표현은 일반적이며 모든 waveform을 나타낼 수 있지만 바이어스에서 자유롭지는 않다. 이는 진동이 아닌 정렬된 웨이브 패킷으로 오디오를 생성하는 것보다 prior를 적용하는 경우가 많기 때문이다. 예를 들어 strided convolution model은 프레임이 겹치는 waveform을 직접 생성한다. 오디오는 고정 프레임 hop size에서 서로 다른 주기로 여러 주파수에서 진동하기 때문에 모델은 서로 다른 프레임 간에 waveform을 정확하게 정렬하고 가능한 모든 위상 변화를 처리하기 위해 필터를 학습해야 한다. 이 효과는 위 그림의 왼쪽 다이어그램에서 볼 수 있다.

Tacotron이나 GANSynth와 같은 푸리에 기반 모델도 STFT(Short-time Fourier Transform)가 윈도우 웨이브 패킷에 대한 표현이기 때문에 위상 정렬 문제가 있다. 또한 푸리에 기본 주파수가 오디오와 완벽하게 일치하지 않을 때 단일 정현파를 나타내기 위해 여러 인접 주파수 및 위상의 정현파를 결합해야 하는 spectral leakage와 싸워야 한다. 이 효과는 위 그림의 중간 다이어그램에서 볼 수 있다.

WaveNet, SampleRNN, WaveRNN과 같은 autoregressive waveform model은 한 번에 단일 샘플 waveform을 생성하여 이러한 문제를 방지한다. 웨이브 패킷 생성에 대한 바이어스에 의해 제한되지 않으며 모든 waveform을 표현할 수 있다. 그러나 진동에 대한 바이어스를 이용하지 않기 때문에 더 크고 더 많은 데이터를 필요로 하는 네트워크가 필요하다. 또한 학습 중 teacher-forcing을 사용하면 오차가 누적되는 exposure bias이 발생한다. 또한 spectral feature, 사전 학습된 모델, discriminator와 같은 perceptual loss들과 호환되지 않는다. 이는 waveform의 모양이 perception과 완벽하게 일치하지 않기 때문에 이러한 모델에 비효율성을 더한다. 예를 들어, 위 그림의 오른쪽에 있는 3개의 waveform은 동일하게 들리지만 autoregressive model에 대해 서로 다른 loss를 나타낸다.

Waveform이나 푸리에 계수를 예측하는 대신 세 번째 모델 클래스는 oscillator로 오디오를 직접 생성한다. Vocoder 또는 신디사이저로 알려진 이러한 모델은 오랜 연구 및 응용 역사를 가지고 있다. 이러한 “분석/합성” 모델은 전문 지식과 손으로 조정한 휴리스틱을 사용하여 해석 가능하고(음량 및 주파수) 생성 알고리즘(합성)에서 사용할 수 있는 합성 파라미터(분석)를 추출한다.

신경망은 이전에 미리 추출된 합성 파라미터를 모델링하는 데 일부 사용되었지만 이러한 모델은 end-to-end 학습에 미치지 못한다. 분석 파라미터는 여전히 손으로 튜닝해야 하며 기울기는 합성 절차를 통해 흐를 수 없다. 결과적으로 파라미터의 작은 오차는 네트워크로 다시 전파할 수 없는 오디오의 큰 오차로 이어질 수 있다. 결정적으로, vocoder의 현실감은 주어진 분석/합성 쌍의 표현력에 의해 제한된다.

본 논문에서는 DDSP 라이브러리를 사용하여 완전히 미분 가능한 신디사이저와 오디오 효과를 구현함으로써 위에서 설명한 한계를 극복한다. DDSP 모델은 위 접근 방식의 강점을 결합하여 oscillator 사용의 inductive bias(유도 편향)로부터 이점을 얻으면서 신경망과 end-to-end 학습의 표현력을 유지한다.

DDSP COMPONENTS

많은 DSP (Digital Signal Processing) 연산은 최신 자동 미분 소프트웨어의 함수로 표현될 수 있다. 핵심 구성 요소를 피드포워드 함수로 표현하여 GPU와 같은 병렬 하드웨어에서 효율적으로 구현하고 학습 중 샘플을 생성할 수 있다. 이러한 구성 요소에는 oscillator, envelopes, filter(LTV-FIR)가 포함된다.

1. Spectral Modeling Synthesis

여기서는 DDSP 모델의 예로 Spectral Modeling Synthesis (SMS)의 미분 가능한 버전을 구현한다. 이 모델은 가산 신디사이저(여러 정현파 합산)와 감산 신디사이저(white noise 필터링)를 결합하여 사운드를 생성한다. 저자들이 SMS를 선택한 이유는 SMS가 매우 표현력이 풍부한 사운드 모델이고 spectral morphing, 시간 스트레칭, 피치 이동, 소스 분리, 전사(transcription), 심지어 MPEG-4에서의 범용 오디오 코덱과 같은 다양한 task에서 널리 채택되었기 때문이다.

저자들은 이 실험에서 단음파 소스만 고려하기 때문에 정현파를 기본 주파수의 정수배로 제한하는 Harmonic plus Noise 모델을 사용한다. 다른 많은 모델보다 SMS의 표현력이 뛰어난 이유 중 하나는 SMS가 더 많은 파라미터를 가지고 있기 때문이다. 예를 들어 여기에서 고려한 데이터셋의 4초 16kHz 오디오에서 신디사이저 계수는 실제로 오디오 waveform 자체보다 2.5배 더 많은 차원을 가진다. 이러한 모든 파라미터를 수작업으로 지정하는 것은 현실적으로 어렵기 때문에 신경망으로 제어할 수 있다.

2. Harmonic Oscillator / Additive Synthesizer

본 논문에서 탐구하는 합성 기술의 핵심은 sinusoidal oscillator이다. Discrete한 timestep $n$에 걸쳐 신호 $x(n)$을 출력하는 oscillator들은 다음과 같이 표현할 수 있다.

\[\begin{equation} x(n) = \sum_{k=1}^K A_k (n) \sin (\phi_k (n)) \end{equation}\]

여기서 $A_k (n)$은 $k$번째 정현파 성분의 진폭이고 $\phi_k (n)$은 순간 위상이다. $\phi_k (n)$은 순간 주파수 $f_k (n)$을 적분하여 구한다.

\[\begin{equation} \phi_k (n) = 2\pi \sum_{m=0}^n f_k (m) + \phi_{0,k} \end{equation}\]

여기서 $\phi_{0,k}$는 랜덤화되거나, 고정되거나, 또는 학습될 수 있는 초기 위상이다.

Harmonic oscillator의 경우 모든 정현파 주파수는 기본 주파수 $f_0 (n)$의 정수배, 즉 $f_k (n) = k f_(n)$이므로 harmonic oscillator의 출력은 전적으로 시간에 따라 변하는 기본 주파수 $f_0 (n)$과 진폭 $A_k (n)$을 변경한다. 해석을 돕기 위해 진폭을 추가로 분해한다.

\[\begin{equation} A_k (n) = A(n) c_k (n) \end{equation}\]

$\sum_{k=0}^K c_k (n) = 1$이고 $c_k (n) \ge 0$인 경우 스펙트럼 변화를 결정하는 harmonic $c(n)$에 대한 loudness와 정규화된 분포를 제어하는 글로벌한 진폭 $A(n)$으로 변환한다. 또한 수정된 sigmoid nonlinearity를 사용하여 진폭과 harmonic 분포 구성 요소가 둘 다 양수가 되도록 제한한다.

3. Envelopes

위의 oscillator 공식에는 오디오 샘플 속도에서 시간에 따라 변하는 진폭과 주파수가 필요하지만 신경망은 더 느린 프레임 속도에서 작동한다. 순간 주파수 업샘플링의 경우 이중 bilinear interpolation이 적합하다. 그러나 가산 신디사이저의 진폭과 harmonic 분포는 아티팩트를 방지하기 위해 부드럽게 만들어 주어야 했다. 저자들은 각 프레임의 중앙에 겹치는 Hamming window를 추가하고 진폭에 의해 크기를 조정하여 부드러운 진폭 envelope로 이를 달성하였다.

4. Filter Design: Frequency Sampling Method

선형 필터 설계는 많은 DSP 기술의 초석이다. 표준 convolution layer는 linear time invariant finite impulse response (LTI-FIR) 필터와 동일하다. 그러나 해석 가능성을 보장하고 위상 왜곡을 방지하기 위해 주파수 샘플링 방법을 사용하여 네트워크 출력을 선형 위상 필터의 임펄스 응답으로 변환한다.

모든 출력 프레임에 대해 FIR 필터의 주파수 도메인 전달 함수(transfer function)를 예측하는 신경망을 설계한다. 특히, 신경망은 출력의 $l$번째 프레임에 대해 벡터 $H_l$을 출력하며, $H_l$을 해당 FIR 필터의 주파수 도메인 전달 함수로 해석한다. 따라서 시간에 따라 변하는 FIR 필터를 구현한다.

시간에 따라 변하는 FIR 필터를 입력에 적용하기 위해 오디오를 겹치지 않는 프레임 $x_l$로 나누어 임펄스 응답 $h_l$과 일치시킨다. 그런 다음 푸리에 도메인에서 프레임들의 곱셈을 통해 프레임별 convolution을 수행한다.

\[\begin{equation} Y_l = H_l \times X_l \\ X_l = \textrm{DFT} (x_l), \quad Y_l = \textrm{DFT} (y_l) \end{equation}\]

여기서 $X_l$과 $Y_l$은 출력이다. 프레임별로 필터링된 오디오 $yl = \textrm{IDFT}(Y_l)$을 복구한 다음 원래 입력 오디오를 분할하는 데 사용된 동일한 hop size와 window로 결과 프레임을 중첩하여 더한다. Hop size는 컨디셔닝의 각 프레임에 대해 오디오를 동일한 간격의 프레임으로 나누어 지정된다. 64,000개의 샘플과 250개의 프레임에 대해 256의 hop size에 해당한다.

실제로는 신경망 출력을 $H_l$로 직접 사용하지 않는다. 그 대신, 신경망 출력에 window function $W$를 적용하여 $H_l$을 계산한다. Window의 모양과 크기는 필터의 시간-주파수 분해능 trade-off를 제어하기 위해 독립적으로 결정할 수 있다. 본 논문의 실험에서는 크기가 257인 Hann window를 기본값으로 사용한다. Window가 없으면 많은 경우에 해상도는 적합하지 않은 직사각형 window로 기본 설정된다. Window를 적용하기 전에 IR을 zero-phase (대칭) 형태로 shift하고 필터를 적용하기 전에 원래 형태로 되돌린다.

5. Filtered Noise / Subtractive Synthesizer

자연음에는 harmonic 성분과 확률 성분이 모두 포함되어 있다. Harmonic plus Noise model은 가산 신디사이저의 출력을 필터링된 noise 스트림과 결합하여 이를 캡처한다. 위의 LTV-FIR 필터를 uniform noise $Y_l = H_l N_l$의 스트림에 간단히 적용하여 미분 가능한 필터링된 noise 신디사이저를 만들 수 있다. 여기서 $N_l$은 도메인 $[-1, 1]$에서 uniform noise의 IDFT이다.

6. Reverb: Long Impulse Responses

잔향(리버브)은 일반적으로 신경망 합성 알고리즘에 의해 암시적으로 모델링되는 사실적인 오디오의 필수 특성이다. 대조적으로 실내 잔향을 합성 후 convolution step으로 명시적으로 분해하여 해석 가능성을 얻는다. 현실적인 실내 임펄스 응답(IR)은 몇 초 정도로 길 수 있으며, 이는 매우 긴 convolutional kernel size (~1-10만 timestep)에 해당한다. 행렬 곱셈을 통한 convolution은 $O(n^3)$이며, 큰 kernel size에서는 다루기 어렵다. 대신 주파수 도메인에서 곱셈으로 convolution을 명시적으로 수행하여 잔향을 구현한다. 이는 $O(n \log n)$이 되고 학습에 병목 현상이 발생하지 않는다.

Experiments

1. DDSP Autoencoder

DDSP 구성 요소는 생성 모델의 선택에 제약을 두지 않지만 여기에서는 여기에서는 adversarial training, variational inference, Jacobian design에 대한 특정 접근 방식과 독립적인 DDSP 구성 요소의 강도를 조사하기 위해 deterministic한 오토인코더에 중점을 둔다. Convolution layer를 사용하는 오토인코더가 fully-connect된 오토인코더보다 이미지에서 성능이 뛰어난 것처럼 DDSP 구성 요소가 오디오 도메인에서 오토인코더 성능을 획기적으로 향상시킬 수 있다. 확률적 latent를 도입하면 성능이 더 향상될 가능성이 높지만 본 논문에서 조사하는 DDSP 구성 요소 성능의 핵심 질문에 벗어나므로 본 논문에서는 사용하지 않는다.

표준 오토인코더에서 인코더 네트워크 \(f_\textrm{enc}(\cdot)\)는 입력 $x$를 latent 표현 \(z = f_\textrm{enc}(x)\)에 매핑하고 디코더 네트워크 \(f_\textrm{dec}(\cdot)\)는 입력 \(\hat{x} = f_\textrm{dec}(z)\)를 직접 재구성하려고 시도한다. 본 논문의 아키텍처는 DDSP 구성 요소와 분해된 latent 표현을 사용하여 이 접근 방식과 대조된다.

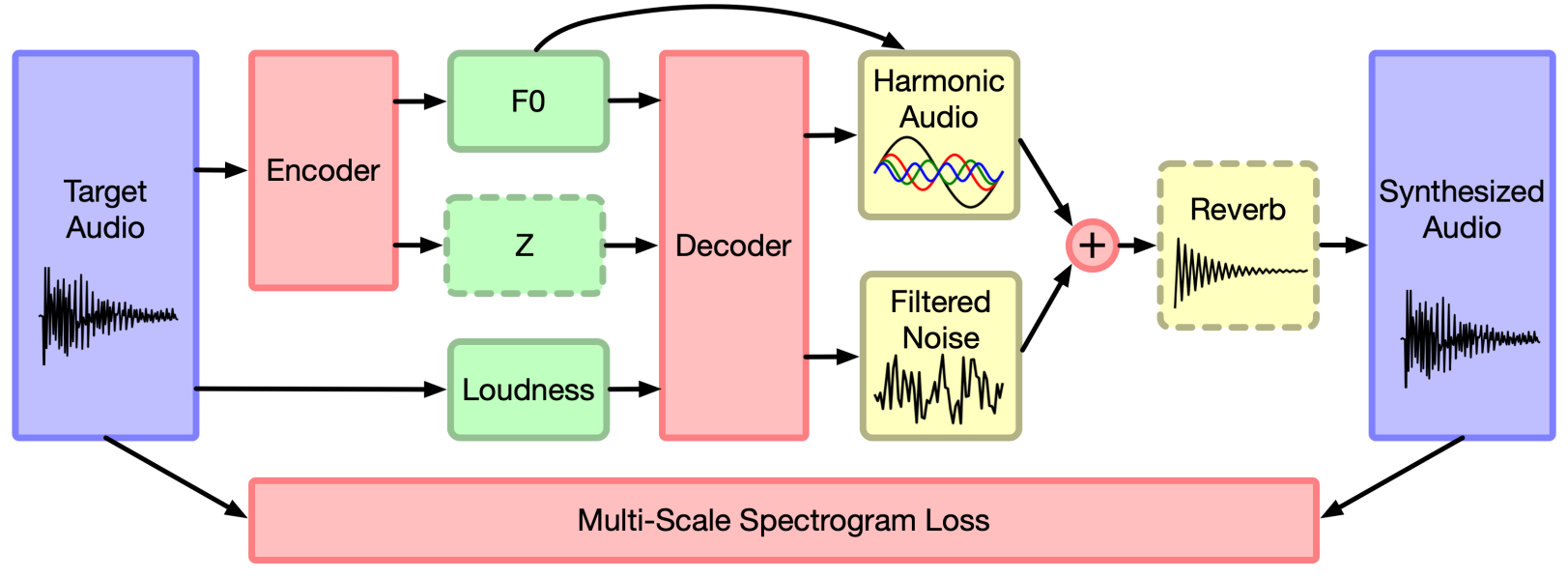
Encoder

Supervised 오토인코더의 경우 오디오에서 loudness $l(t)$를 직접 추출하고, 사전 학습된 CREPE 모델을 $f(t)$ 인코더로 사용하여 기본 주파수를 추출하며, 선택적 인코더는 residual 정보의 latent 인코딩 $z(t)$를 추출한다. $z(t)$ 인코더의 경우 MFCC 계수(프레임당 30개)가 먼저 오디오에서 추출되며 이는 harmonics의 부드러워진 spectral envelope에 해당하고 단일 GRU layer에 의해 각 프레임당 16개의 latent 변수로 변환된다.

Unsupervised 오토인코더의 경우 사전 학습된 CREPE 모델은 오디오의 mel-scaled log spectrogram에서 $f(t)$를 추출하는 Resnet 아키텍처로 대체되고 나머지 네트워크와 공동으로 학습된다.

Decoder

디코더 네트워크는 튜플 $(f(t), l(t), z(t))$을 가산 신디사이저와 필터링된 noise 신디사이저에 대한 제어 파라미터에 매핑한다. 신디사이저는 이러한 파라미터를 기반으로 오디오를 생성하고 합성된 오디오와 원본 오디오 사이의 reconstruction loss가 최소화된다. 네트워크 아키텍처는 좋은 품질을 가능하게 하는 것이 다른 모델링 결정이 아니라 DDSP 구성 요소임을 입증하기 위해 상당히 일반적이도록 선택되었다.

또한 latent $f(t)$는 주어진 데이터셋의 컨텍스트 외부에서 신디사이저에 대한 구조적 의미를 갖기 때문에 가산 신디사이저에 직접 공급된다. 이 disentangle된 표현을 통해 모델은 데이터 분포 내에서 interpolate(보간)하고 외부에서 extrapolate(외삽)할 수 있다.

2. Multi-Scale Spectral Loss

오토인코더의 주요 목적은 reconstruction loss를 최소화하는 것이다. 그러나 오디오 waveform의 경우 waveform의 point-wise loss는 이상적이지 않다. 지각적으로 동일한 두 개의 오디오 샘플이 뚜렷한 waveform을 가질 수 있고 point-wise하게 유사한 waveform이 매우 다르게 들릴 수 있기 때문이다.

대신 다음과 같이 정의된 multi-resolution spectral amplitude distance와 유사한 multi-scale spectral loss를 사용한다. 원본 오디오와 합성된 오디오가 주어지면 주어진 FFT 크기 $i$로 각각 spectrogram $S_i$ 및 $\hat{S}_i$를 계산하고 loss를 $S_i$와 $\hat{S}_i$ 사이의 L1 차이와 $\log S_i$와 $\log \hat{S}_i$ 사이의 L1 차이의 합으로 정의한다.

\[\begin{equation} L_i = \| S_i - \hat{S}_i \|_1 + \alpha \| \log S_i - \log \hat{S}_i \|_1 \end{equation}\]

여기서 $\alpha$는 실험에서 1.0으로 설정된 가중 항이다. 총 reconstruction loss는 모든 spectral loss의 합

\[\begin{equation} L_\textrm{reconstruction} = \sum_i L_i \end{equation}\]

이다. 실험에서 저자들은 FFT 크기 (2048, 1024, 512, 256, 128, 64)를 사용했으며 STFT에서 인접 프레임이 75% 겹친다. 따라서 $L_i$는 서로 다른 시공간적 해상도에서 원본 오디오와 합성된 오디오 간의 차이를 커버한다.

Results

1. High-Fidelity Synthesis

다음은 솔로 바이올린 클립을 분해한 것이다.

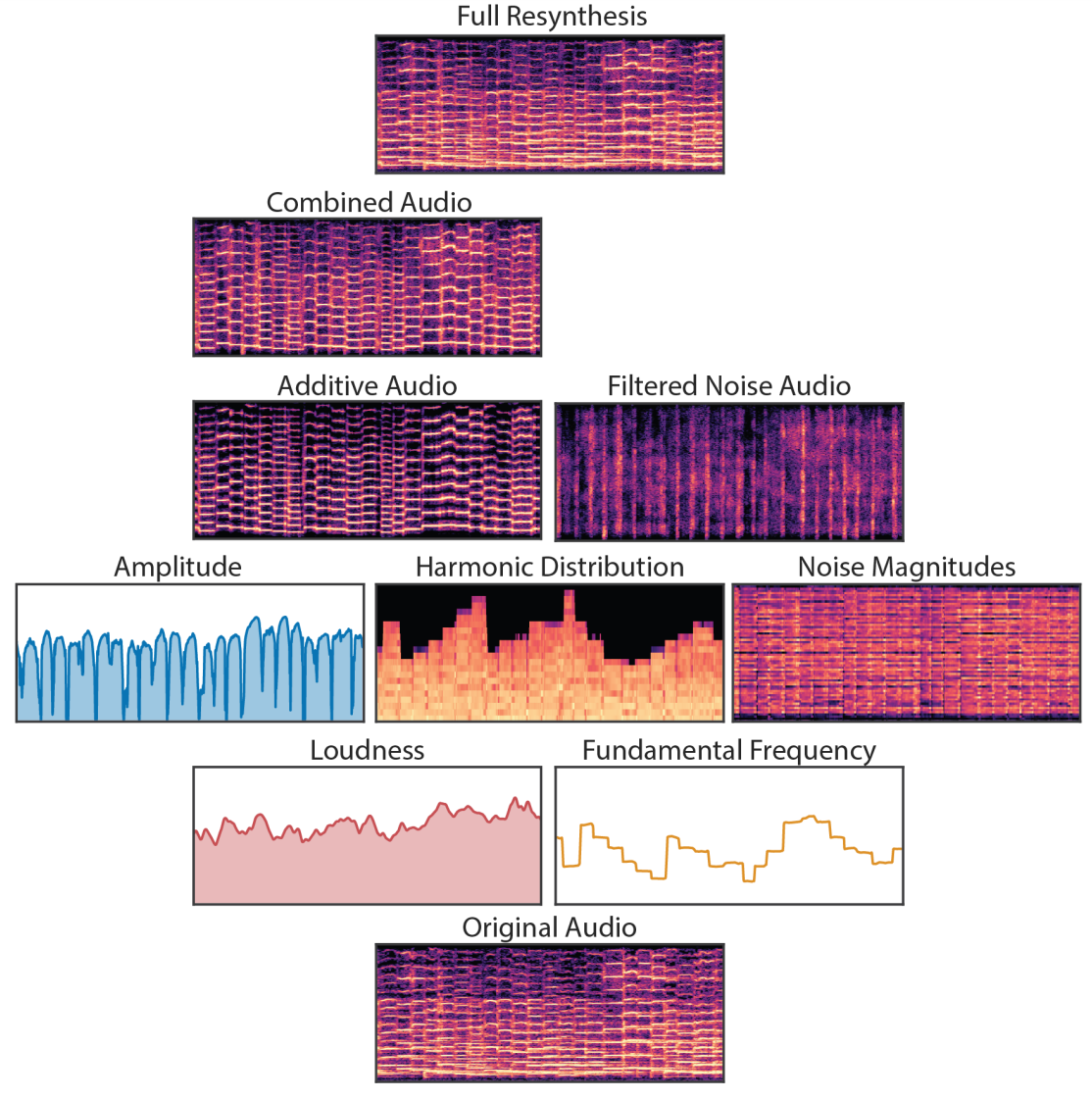
DDSP 오토인코더는 솔로 바이올린 데이터셋을 매우 정확하게 재합성하는 방법을 학습한다. 이전에는 고품질 오디오 합성을 위해 매우 큰 autoregressive model 또는 adversarial loss function이 필요했다. Adversarial loss에 순응하는 대신 DDSP 오토인코더는 간단한 L1 spectrogram loss, 적은 양의 데이터, 상대적으로 간단한 모델로 이러한 결과를 달성한다. 이는 모델이 신경망의 표현력을 잃지 않으면서 DSP 구성 요소의 바이어스를 효율적으로 활용할 수 있음을 보여준다.

다음은 재합성 정확도에 대한 표이다.

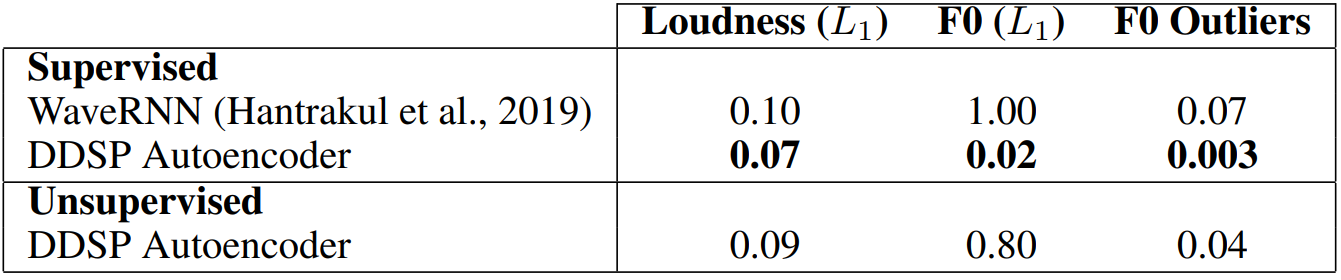
2. Independent Control of Loudness and Pitch

다음은 loudness, pitch, 음색에 대한 별도의 interpolation 결과이다.

컨디셔닝 feature(실선)는 두 개의 음표에서 추출되고 선형으로 혼합된다 (어두운 색에서 밝은 색으로). 재합성된 오디오의 feature(점선)는 컨디셔닝을 밀접하게 따른다.

3. Dereverberation and Acoustic Transfer

다음은 disentanglement와 extrapolation을 통해 DDSP가 해석 가능한 모델임을 보여주는 그림이다.

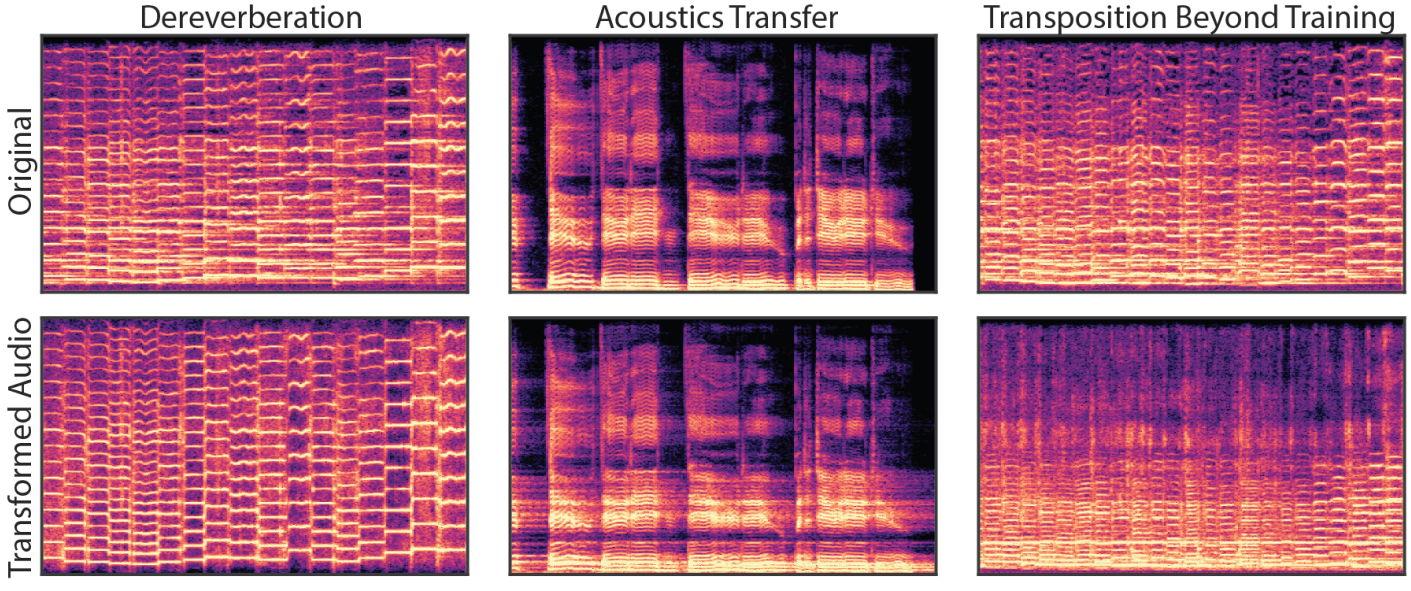
왼쪽 그림은 재합성 중에 리버브 모듈을 우회하면 무향실에서 녹음하는 것과 유사하게 잔향이 완전히 제거된 오디오를 생성한다는 것을 보여준다. 접근 방식의 품질은 기본 생성 모델에 의해 제한되며, 이는 오토인코더에 대해 상당히 높다. 마찬가지로, 가운데 그림은 학습된 리버브 모델을 새로운 오디오에 적용할 수 있고 솔로 바이올린 녹음의 음향 환경을 효과적으로 transfer할 수 있음을 보여준다.

4. Timbre Transfer

노래하는 목소리에서 바이올린으로 음색을 transfer한 예시이다.

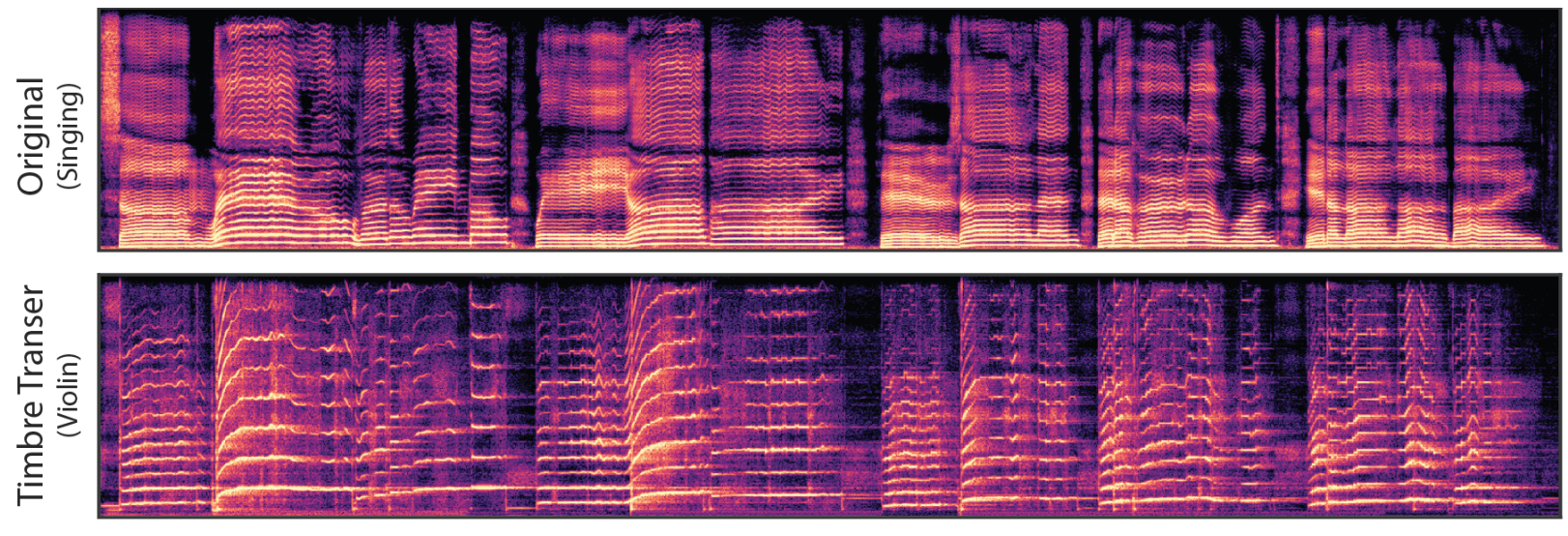
F0와 loudness feature는 노래하는 목소리와 재합성에 사용되는 솔로 바이올린에 대해 학습된 DDSP 오토인코더에서 추출된다. 컨디셔닝 feature를 더 잘 일치시키기 위해 먼저 노래하는 목소리의 기본 주파수를 바이올린의 일반적인 음역에 맞게 2옥타브 이동한다. 다음으로 바이올린 녹음의 실내 음향을 음성으로 transfer한 후 음량을 추출하여 바이올린 녹음의 음량 윤곽에 더 잘 맞춘다. 결과 오디오는 바이올린 데이터셋의 음색 및 실내 음향으로 노래의 많은 미묘함을 캡처한다.