[논문리뷰] Few-shot Image Generation with Diffusion Models (DDPM-PA)
arXiv 2022. [Paper]
Jingyuan Zhu, Huimin Ma, Jiansheng Chen, Jian Yuan
Tsinghua University | University of Science and Technology Beijing
7 Nov 2022
Introduction
GAN, VAE, autoregressive model을 포함한 생성 모델의 최근 발전으로 다양성이 뛰어난 고품질 이미지 생성이 실현되었다. Diffusion model은 여러 step의 noising process를 reverse시키는 방법을 학습하여 데이터 분포를 일치시키기 위해 도입되었다. DDPM은 고품질 결과를 생성하는 능략을 보여주었다. 이후의 연구들은 noise schedule, 네트워크 아키텍처, DDPM의 최적화 목적 함수를 더욱 최적화하였다. 또한 DDPM 기반 조건부 이미지 생성을 구현하기 위해 classifier guidance가 추가되었다. DDPM은 여러 데이터 셋에서 GAN과 경쟁할 수 있는 우수한 생성 결과를 보여주었다. 또한 DDPM은 동영상, 오디오, 포인트 클라우드, 생물학적 구조를 생성하는 데 있어 뛰어난 결과를 달성했다.
최신 DDPM은 다른 생성 모델과 마찬가지로 네트워크에서 수백만 개의 파라미터를 학습하기 위해 많은 양의 데이터에 의존한다. DDPM은 학습 데이터가 제한될 때 심각하게 overfitting되고 상당한 다양성을 가진 고품질 이미지를 생성하지 못하는 경향이 있다. 불행히도 어떤 상황에서는 풍부한 데이터를 얻는 것이 항상 가능한 것은 아니다. 몇 가지 사용 가능한 학습 샘플을 사용하여 대규모 소스 데이터셋에서 사전 학습된 모델을 대상 데이터셋에 적용하기 위해 일련의 GAN 기반 접근 방식이 제안되었다. 이러한 접근 방식은 소스 모델의 지식을 활용하여 overfitting을 완화하지만 제한된 품질과 다양성만 달성할 수 있다. 또한 제한된 데이터에 대해 학습된 DDPM의 성능과 실용적인 DDPM 기반의 few-shot 이미지 생성 접근 방식은 아직 연구되지 않았다.
저자들은 먼저 소규모 데이터셋에서 학습된 DDPM의 성능을 평가하고 제한된 데이터에서 학습될 때 DDPM이 다른 최신 생성 모델과 유사한 overfitting 문제를 겪는다는 것을 보여주었다. 그런 다음 제한된 데이터를 직접 사용하여 타겟 도메인에서 사전 학습된 DDPM을 fine-tuning한다. Fine-tuning된 DDPM은 처음부터 학습된 DDPM에 비해 더 빠른 수렴과 다양한 생성 샘플을 달성하지만 여전히 유사한 feature를 공유하고 고주파수 디테일이 누락된 결과를 얻는다. 이를 위해 생성된 샘플 사이의 상대적인 거리를 유지하고 도메인 적응 중에 고주파 디테일 향상을 실현하여 매우 다양한 고품질의 few-shot 이미지 생성을 달성하는 DDPM-PA (DDPM pairwise adaptation)을 도입하였다.
DDPMs Trained on Small-scale Datasets
저자들은 학습 데이터가 제한적일 때 DDPM의 성능을 평가하기 위해 처음부터 다양한 수의 이미지가 포함된 소규모 데이터 셋에서 DDPM을 학습하였다. 학습 샘플이 감소함에 따라 DDPM이 overfitting되는 시기를 연구하기 위해 생성 다양성을 정성적 및 정량적으로 분석하였다.
Basic Setups
- 데이터셋
- FFHQ-babies (Babies), FFHQ-sunglasses (Sunglasses), LSUN Church에서 각각 10, 100, 1000개의 이미지를 소규모 학습 데이터셋으로 샘플링
- 모든 데이터셋트의 이미지 해상도는 256$\times$256으로 설정
- 학습 디테일
- 최대 diffuseit step $T = 1000$
- Learning rate: $10^{-4}$
- Batch size: 48
- 10개 또는 100개의 이미지가 포함된 데이터셋에서 4만 iteration으로 학습하고 1000개 이미지가 포함된 데이터셋에서 6만 iteration으로 학습
Qualitative Evaluation
다음은 작은 스케일의 Sunglasses 데이터셋에서 학습된 DDPM이 생성한 샘플들이다.

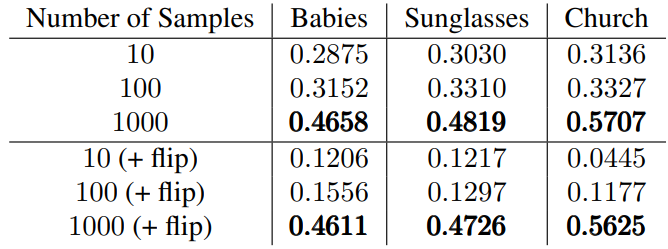
Quantitative Evaluation
다음은 다양한 작은 스케일의 데이터셋들에서 학습된 DDPM의 Nearest-LPIPS 결과이다.
Method
DDPM 기반의 few-shot 이미지 생성을 구현하기 위해 먼저 제한된 타겟 데이터를 직접 사용하여 대규모 소스 데이터셋에서 사전 학습된 DDPM을 fine-tuning한다. Fine-tuning된 모델은 수렴하는 데 3천에서 4천 번의 iteration만 필요하다.

위 그림의 가운데 줄에서 볼 수 있듯이 10개의 학습 샘플만으로 다양한 결과를 얻을 수 있다. 그러나 생성된 샘플은 고주파 디테일이 충분하지 않고 헤어스타일과 얼굴 표정과 같은 유사한 feature를 공유하여 생성 품질과 다양성이 저하된다.
사전 학습된 모델과 비교하여 fine-tuning된 모델의 저하는 주로 생성된 샘플 간의 상대적 거리가 지나치게 짧아지는 데서 비롯된다.
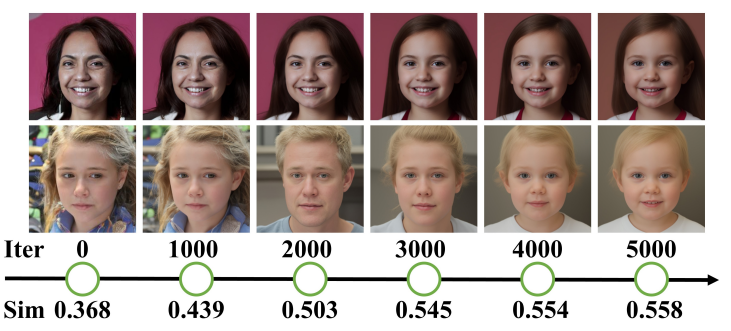
위 그림에서 볼 수 있듯이 직접 fine-tuning된 DDPM에 의해 고정된 noise 입력에서 합성된 두 개의 샘플은 학습을 통해 점점 더 유사해지며 다양한 feature와 고주파수 디테일 정보가 손실된다.
따라서 본 논문은 소스 샘플과 유사한 적응된 샘플 사이의 상대적 쌍별 거리를 유지하여 도메인 적응 프로세스를 정규화할 것을 제안한다. 또한 제한된 데이터에서 고주파수 디테일을 학습하고 소스 도메인에서 학습한 고주파수 디테일을 보존하도록 적응된 모델을 가이드한다.
본 논문의 접근 방식은 소스 모델을 수정된 모델에 대한 레퍼런스로 수정한다. 적응 모델의 가중치는 소스 모델의 가중치로 초기화되고 타겟 도메인에 적응된다. 제안된 DDPM-PA 접근 방식의 개요는 10-shot FFHQ $\rightarrow$ Babies를 예로 사용하여 아래 그림에 설명되어 있다.
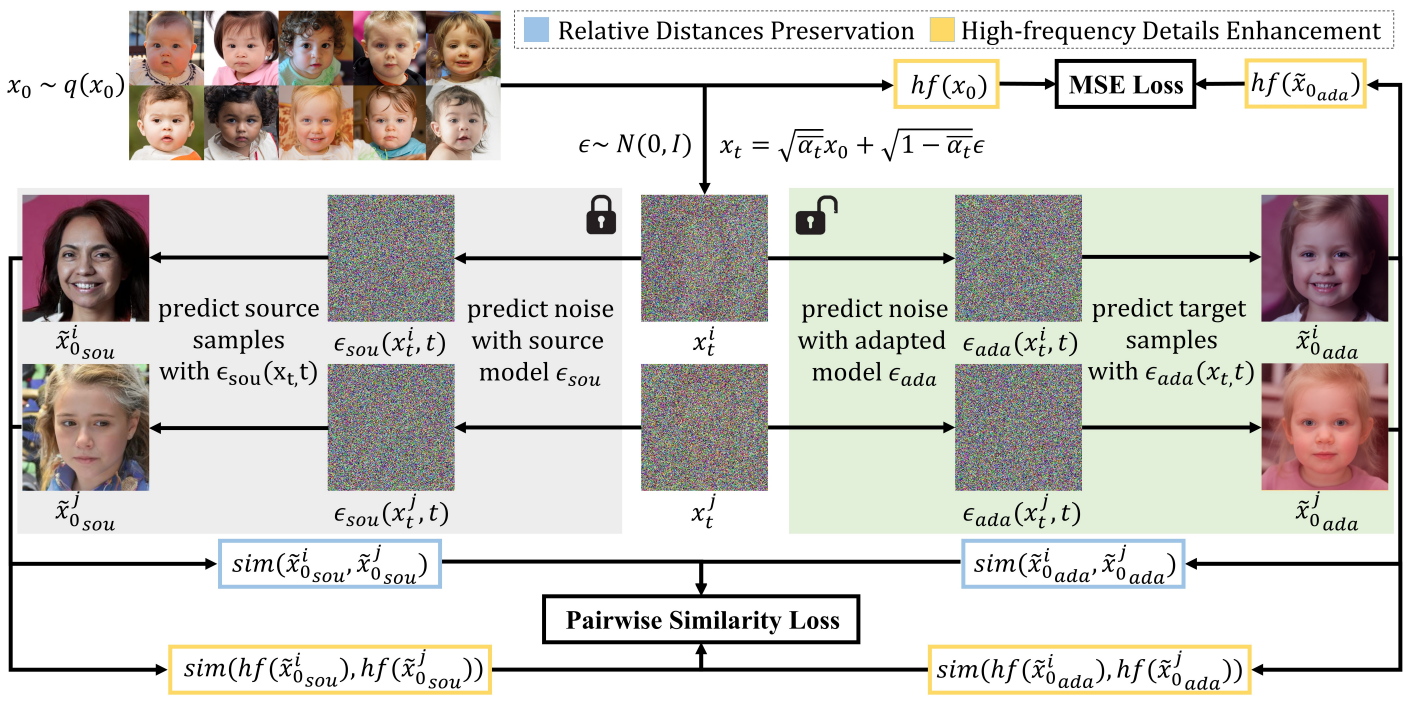
1. Relative Distances Preservation
저자들은 도메인 적응 중에 생성된 샘플 사이의 상대적인 거리를 보존하기 위해 쌍별 유사도 loss를 설계하였다. 각 이미지에 대한 N-방향 확률 분포를 구성하기 위해 학습 샘플 $x_0 \sim q(x_0)$에 랜덤으로 Gaussian noise를 추가하여 noisy한 이미지 배치 \(\{x_t^n\}_{n=0}^N\)을 샘플링한다. 완전히 denoise된 이미지 \(\{\tilde{x}_0^n\}_{n=0}^N\)을 예측하기 위해 모델이 적용된다. $x_t$와 $\epsilon_\theta(x_t, t)$의 관점에서 \(\tilde{x}_0\)의 예측은 다음과 같다.
\[\begin{equation} \hat{x}_0 = \frac{1}{\sqrt{\vphantom{1} \bar{\alpha}_t}} x_t - \frac{\sqrt{1 - \bar{\alpha}_t}}{\sqrt{\vphantom{1} \bar{\alpha}_t}} \epsilon_\theta (x_t, t) \end{equation}\]코사인 유사도는 예측된 샘플들 \(\tilde{x}_0\) 사이의 상대적 거리를 측정하는 데 사용된다. 소스 모델과 적응 모델에서 \(\tilde{x}_0^i (0 \le i \le N)\)에 대한 확률 분포는 다음과 같이 표현할 수 있다.
\[\begin{equation} p_i^\textrm{sou} = \textrm{sfm} (\{ \textrm{sim} (\tilde{x}_{0_\textrm{sou}}^i, \tilde{x}_{0_\textrm{sou}}^j) \}_{\forall i \ne j}) \\ p_i^\textrm{ada} = \textrm{sfm} (\{ \textrm{sim} (\tilde{x}_{0_\textrm{ada}}^i, \tilde{x}_{0_\textrm{ada}}^j) \}_{\forall i \ne j}) \end{equation}\]여기서 $\textrm{sim}$과 $\textrm{sfm}$은 각각 코사인 유사도와 softmax 함수이다. 그러면 생성된 이미지에 대한 쌍별 유사도 loss는 다음과 같다.
\[\begin{equation} \mathcal{L}_\textrm{img} (\epsilon_\textrm{sou}, \epsilon_\textrm{ada}) = \mathbb{E}_{t, x_0, \epsilon} \sum_i D_\textrm{KL} (p_i^\textrm{ada} \| p_i^\textrm{sou}) \end{equation}\]2. High-frequency Details Enhancement
먼저 일반적인 Haar wavelet transformation을 사용하여 이미지를 여러 주파수 성분로 분리한다. Haar wavelet transformation에는 $\textrm{LL}^\top$, $\textrm{LH}^\top$, $\textrm{HL}^\top$, $\textrm{HH}^\top$를의 4개의 커널이 포함되며, 여기서 $\textrm{L}$과 $\textrm{H}$는 각각 low pass filter와 high pass filter를 나타낸다.
\[\begin{equation} \textrm{L}^\top = \frac{1}{\sqrt{2}} [1,1], \quad \textrm{H}^\top = \frac{1}{\sqrt{2}} [-1, 1] \end{equation}\]Haar wavelet transformation은 $\textrm{LL}$, $\textrm{LH}$, $\textrm{HL}$, $\textrm{HH}$의 4가지 주파수 성분으로 분해할 수 있다. $\textrm{LL}$은 이미지의 기본 구조를 포함하며, 다른 고주파 성분들은 이미지의 풍부한 디테일을 포함한다. $\textrm{hf}$를 이 고주파 성분의 합으로 정의한다.
\[\begin{equation} \textrm{hf} = \textrm{LH} + \textrm{HL} + \textrm{HH} \end{equation}\]두 가지 관점에서 고주파 디테일 향상을 구현한. 첫째, 제안된 쌍별 유사도 loss를 사용하여 소스 도메인에서 학습된 고주파수 디테일을 보존한다. 유사하게, 소스 모델과 적응 모델에서 \(\tilde{x}_0^i (0 \le i \le N)\)의 고주파 성분에 대한 확률 분포와 생성된 샘플에서 고주파 성분에 대한 쌍별 유사도 loss는 다음과 같다.
\[\begin{equation} \textrm{pf}_i^\textrm{sou} = \textrm{sfm} (\{ \textrm{sim} (\textrm{hf} (\tilde{x}_{0_\textrm{sou}}^i), \textrm{hf} (\tilde{x}_{0_\textrm{sou}}^i)) \}_{\forall i \ne j} ) \\ \textrm{pf}_i^\textrm{ada} = \textrm{sfm} (\{ \textrm{sim} (\textrm{hf} (\tilde{x}_{0_\textrm{ada}}^i), \textrm{hf} (\tilde{x}_{0_\textrm{ada}}^i)) \}_{\forall i \ne j} ) \\ \mathcal{L}_\textrm{hf} (\epsilon_\textrm{sou}, \epsilon_\textrm{ada}) = \mathbb{E}_{t, x_0, \epsilon} \sum_i D_\textrm{KL} (\textrm{pf}_i^\textrm{ada} \;\|\; \textrm{pf}_i^\textrm{sou}) \end{equation}\]둘째, 다음과 같이 적응된 샘플 \(\tilde{x}_0\)와 학습 데이터 $x_0$의 고주파 성분 사이의 평균 제곱 오차를 최소화하여 학습 데이터에서 더 많은 고주파수 디테일을 학습하도록 적응된 모델을 가이드한다.
\[\begin{equation} \mathcal{L}_\textrm{hfmsc} = \mathbb{E}_{t, x_0, \epsilon} [\| \textrm{hf} (\tilde{x}_0) - \textrm{hf} (x_0) \|^2] \end{equation}\]3. Overall Optimization Target
DDPM-PA의 전체 최적화 목적 함수는 위에서 언급한 모든 방법을 결합한다.
\[\begin{equation} \mathcal{L} = \mathcal{L}_\textrm{simple} + \lambda_1 \mathcal{L}_\textrm{vlb} + \lambda_2 \textrm{img} + \lambda_3 \mathcal{L}_\textrm{hf} + \lambda_4 \mathcal{L}_\textrm{hfmsc} \end{equation}\]$\lambda_1$은 0.001로 설정하여 \(\mathcal{L}_\textrm{vlb}\)가 \(\mathcal{L}_\textrm{simple}\)을 압도하는 것을 피한다. \(\mathcal{L}_\textrm{img}\)는 적응된 샘플 사이의 상대적인 거리를 보존하기 위해 적응된 모델을 가이드한다. \(\mathcal{L}_\textrm{hfmse}\)와 \(\mathcal{L}_\textrm{hf}\)는 고주파 디테일의 보존을 더욱 향상시킨다. 저자들은 경험적으로 0.1에서 1.0 사이의 범위에 있는 $\lambda_2$, $\lambda_3$과 0.01에서 0.08 사이의 범위에 있는 $\lambda_4$가 few-shot 적응 설정에 효과적이라는 것을 발견했다.
Experiments
다음은 DDPM-PA의 다양한 샘플들이다.

다음은 FFHQ $\rightarrow$ Sunglasses에서의 10-shot 이미지 생성 샘플들이다.

다음은 GAN 기반 baseline들 Intra-LPIPS를 비교한 결과이다.
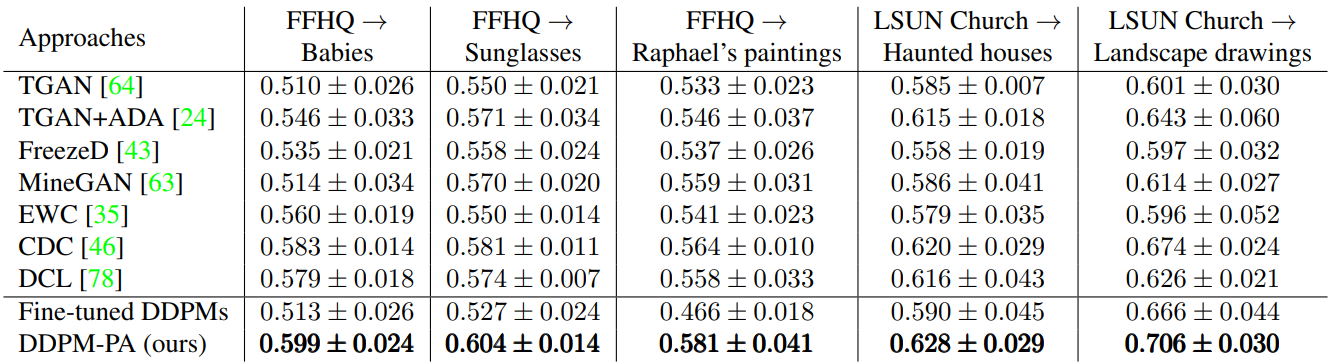
다음은 FFHQ $\rightarrow$ Babies에서 GAN 기반 baseline들과 FID를 비교한 결과이다.
