[논문리뷰] Input Perturbation Reduces Exposure Bias in Diffusion Models (DDPM-IP)
ICML 2023. [Paper] [Github]
Mang Ning, Enver Sangineto, Angelo Porrello, Simone Calderara, Rita Cucchiara
Utrecht University | University of Modena and Reggio Emilia
16 Mar 2023
Introduction
DDPM은 고품질 샘플 생성 능력으로 인해 점점 더 많은 관심을 받고 있는 새로운 생성 패러다임이다. 단일 step에서 새 샘플을 합성하는 대부분의 기존 생성 방법과 달리 DDPM은 Langevin 역학과 유사하며 생성 프로세스는 일련의 denoising step을 기반으로 하며, 여기서 합성 샘플은 순수한 noise에서 시작하여 autoregressive하게 noise 성분을 줄인다. 보다 구체적으로 학습하는 동안 실제 샘플 $x_0$는 Gaussian noise를 추가하여 $T$ steo에서 점진적으로 파괴된다 (forward process). 이렇게 얻은 시퀀스 $x_0, \cdots, x_t, \cdots, x_T$는 forward process를 반전시키기 위해 깊은 denoising autoencoder $\mu$를 학습시키는 데 사용된다.
\[\begin{equation} \hat{x}_{t-1} = \mu (x_t, t) \end{equation}\]Inference 시 생성 프로세스는 이전에 생성된 샘플에 따라 달라지기 때문에 autoregressive하다.
\[\begin{equation} \hat{x}_{t-1} = \mu (\hat{x}_t, t) \end{equation}\]다양한 생성 필드에서 DDPM의 큰 성공에도 불구하고 DDPM의 주요 단점 중 하나는 학습과 inference 단계 모두에서 필요한 많은 step $T$에 따라 계산 시간이 매우 길다는 것이다. $T$가 커야 하는 근본적인 이유는 각 denoising step이 가우시안으로 가정되고 이 가정은 작은 step 크기에만 적용되기 때문이다. 반대로 step 크기가 클수록 예측 네트워크 $\mu$는 더 어려운 문제를 해결해야 하며 점차 정확도가 떨어진다. 그러나 본 논문에서는 샘플링 체인과 관련이 있지만 첫 번째 현상과 부분적으로 대조되는 두 번째 현상이 있음을 관찰하였다. 즉, $T$개의 inference 샘플링 step에서 이러한 오차가 누적된다. 이는 기본적으로 학습 단계와 inference 단계 사이의 불일치 때문이다. Inference 단계에서는 이전 step의 결과를 기반으로 일련의 샘플을 생성하므로 오차가 누적될 수 있다. 사실 학습 시에 $\mu$는 ground-truth 쌍 $(x_t, x_{t−1})$으로 학습되고 $x_t$가 주어지면 $x_{t−1}$을 재구성하는 방법을 학습한다. 그러나 inference 시에 $\mu$는 “실제” $x_t$에 액세스할 수 없으며 예측은 이전에 생성된 \(\hat{x}_t\)에 따라 달라진다. 학습 중에 사용되는 $\mu(x_t, t)$와 테스트 중에 사용되는 \(\mu(\hat{x}_t, t)\) 사이의 입력 불일치는 다른 autoregressive 방법에서 공유하는 exposure bias 문제와 유사하다. 모델이 자체 예측에 노출된 적이 없기 때문에 이전 ground-truth 단어가 주어진 다음 ground-truth 단어의 likelihood를 최대화하도록 네트워크를 학습하면 (Teacher-Forcing), inference 시간에 오차가 누적된다.
본 논문에서는 첫째, 이러한 누적 오차 현상을 실증적으로 분석한다. 예를 들어, $T$ step으로 학습된 표준 DDPM이 inference step $T’ < T$를 사용하여 더 나은 결과를 생성할 수 있음을 보여준다. 이 명백히 대조되는 결과의 이유는 한편으로는 체인이 길수록 reverse process에서 가우시안 가정을 더 잘 충족할 수 있는 반면, 다른 한편으로는 더 큰 오차 누적으로 이어지기 때문이다.
둘째, exposure bias 문제를 완화하기 위해 학습 중 예측 오차를 명시적으로 모델링하는 놀랍도록 간단하면서도 매우 효과적인 방법을 제안한다. 특히 학습 시에 $x_t$를 섭동시키고 $\mu$에 noisy한 $x_t$를 공급한다. 이런 방식으로 학습-inference 불일치를 시뮬레이션하고 학습된 네트워크가 가능한 inference 예측 오차를 고려하도록 한다. 섭동은 새로운 noise가 ground truth 예측 타겟에서 사용되지 않기 때문에 content-destroying forward process와 다르다. 제안된 방법은 네트워크가 예측 함수를 매끄럽도록 강제하는 학습 정규화입이다. 제안된 task를 해결하기 위해 두 개의 공간적으로 가까운 점 $x_1$과 $x_2$는 유사한 예측 $\mu (x_1, t)$와 $\mu(x_2, t)$로 이어져야 한다. 이 정규화 접근 방식은 Mixup 및 VRM principle과 유사하다. 여기에서 학습 데이터의 각 샘플 주변의 이웃이 정의된 다음 타겟 클래스 레이블을 고정한 샘플을 섭동시키는 데 사용된다.
셋째, 입력 섭동을 사용하는 대신 $\mu$가 Lipschitz 연속이 되도록 명시적으로 권장하여 더 매끄러운 예측 함수 $\mu$를 얻는 diffusion model의 exposure bias 문제에 대한 대체 솔루션을 제안한다. 이에 대한 이론적 근거는 Lipschitz 연속 함수 $\mu$가 해당 도메인의 인접 지점 간에 작은 예측 차이를 생성하여 inference 오차에 더 강력한 DDPM을 생성한다는 것이다.
마지막으로, 저자들은 제안된 모든 솔루션을 경험적으로 분석하고, 최종 생성 품질을 개선하는 데 모두 효과적임에도 불구하고 입력 섭동이 DDPM에서 Lipschitz 상수를 명시적으로 최소화하는 것보다 더 효율적이고 효과적이라는 것을 보여준다. 또한 학습 시에 네트워크 입력을 직접 섭동시키는 것은 추가 학습 오버헤드가 없으며 이 솔루션은 재생산이 매우 쉽고 기존 DDPM 프레임워크에 연결된다. 네트워크 아키텍처 또는 loss function을 변경하지 않고 단 두 줄의 코드로 얻을 수 있다. 본 논문의 방법을 DDPM with Input Perturbation (DDPM-IP)라고 부르며 이것이 최신 DDPM의 생성 품질을 크게 향상시킬 수 있음을 보여준다.
Background
일반성을 잃지 않고 이미지 도메인을 가정하고 입력 space에서 diffusion process를 정의하는 DDPM에 중점을 둔다. ADM을 따라 각 픽셀 값이 $[-1, 1]$에 선형적으로 스케일링되었다고 가정한다. 데이터 분포 $q(x_0)$의 샘플 $x_0$와 미리 정의된 noise schedule $(\beta_1, \cdots, \beta_T)$가 주어지면 DDPM은 forward process를 실제 이미지 $x_0 \sim q(x_0)$에서 시작하는 Markov chain으로 정의하고 $T$ diffusion step에 대해 완전히 noisy한 $x_T \sim \mathcal{N}(0,I)$를 얻을 때까지 반복적으로 Gaussian noise를 추가한다.
\[\begin{equation} q(x_t \vert x_{t-1}) = \mathcal{N} (x_t; \sqrt{1 - \beta_t} x_{t-1}, \beta_t I) \\ q(x_{1:T} \vert x_0) = \prod_{t=1}^T q(x_t \vert x_{t-1}) \end{equation}\]반면에 reverse process는 $\theta$로 parameterize된 transition 확률로 정의된다.
\[\begin{equation} p_\theta (x_{t-1} \vert x_t) = \mathcal{N} (x_{t-1}; \mu_\theta (x_t, t), \sigma_t I) \\ \sigma_t = \frac{1 - \bar{\alpha}_{t-1}}{1 - \bar{\alpha}_t} \beta_t, \quad \bar{\alpha}_t = \prod_{i=1}^t \alpha_i, \quad \alpha_i = 1 - \beta_i \end{equation}\]$x_0$가 주어지면, $x_t$는 다음과 같이 얻을 수 있다.
\[\begin{equation} x_t = \sqrt{\vphantom{1} \bar{\alpha}_t} x_0 + \sqrt{1 - \bar{\alpha}_t} \epsilon, \quad \epsilon \sim \mathcal{N}(0,I) \end{equation}\]Forward process posterior의 평균 \(\hat{x}_{t-1} = \mu_\theta (x_t, t)\)을 예측하는 대신, DDPM은 noise 벡터 $\epsilon$을 예측하는 네트워크 $\epsilon_\theta$를 사용할 것을 제안하였다. $\epsilon_\theta$와 간단한 L2 loss function을 사용하면 목적 함수는 다음과 같다.
\[\begin{equation} \mathcal{L} (\theta) = \mathbb{E}_{x_0 \sim q (x_0), \epsilon \sim \mathcal{N} (0, I), t \sim \mathbb{U} (\{1, \cdots, T\})} [\| \epsilon - \epsilon_\theta (x_t, t) \|^2] \end{equation}\]$x_t$와 $\epsilon$은 ground-truth 항이고 $\epsilon_\theta (x_t, t)$는 네트워크 예측이다. 위 식을 사용하여 학습 알고리즘과 샘플링 알고리즘은 각각 Algorithm 1과 2이다.


Exposure Bias Problem in Diffusion Models
Algorithm 1의 line 4와 Algorithm 2의 line 4를 비교하면 예측 네트워크 $\epsilon_\theta$의 입력이 학습 단계와 inference 단계에서 다르다는 것을 알 수 있다. 구체적으로 학습 시에 표준 DDPM은 $\epsilon_\theta (x_t, t)$를 사용한다. 여기서 $x_t$는 ground-truth 샘플이다. 반대로 inference 시에는 \(\epsilon_\theta (\hat{x}_t, t)\)를 사용하는데, 여기서 \(\hat{x}_t\)는 이전 샘플링 step $t+1$에서 $\epsilon_\theta$의 출력을 기반으로 계산된다. 이것은 학습-inference 불일치로 이어진다. 이는 학습 시에는 ground-truth 문장으로 컨디셔닝되지만 inference 시에는 이전에 생성된 단어로 컨디셔닝되는 텍스트 생성 모델에서 관찰된 exposure bias 문제와 유사하다.
Inference 샘플링 step의 수와 관련하여 오차 누적을 정량화하기 위해 (무작위로 선택된) 실제 이미지 $x_0$에서 시작하는 간단한 실험을 하고 $x_t$를 계산한 다음 무작위 $x_T$ 대신 $x_t$에서 시작하는 reverse process를 적용한다. 이렇게 하면 $t$가 충분히 작을 때 네트워크가 $x_0$에 대한 경로를 복구할 수 있어야 한다 (denoising task가 더 쉽다).
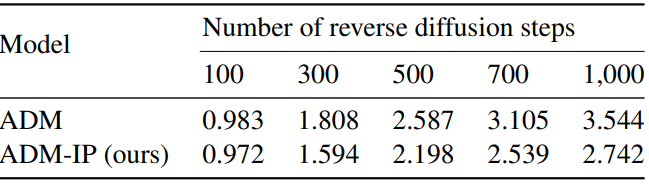
위 표의 FID 점수를 사용하여 ground-truth 분포 $q(x_0)$와 예측 분포 \(q(\hat{x}_0)\)의 차이를 비교하여 $t$ reverse step에서 누적된 총 오차를 정량화한다. 실험은 ADM ($T = 1,000$으로 학습됨)과 ImageNet 32$\times$32를 사용하여 수행되었으며 50k 샘플을 사용하여 FID 점수를 계산한다. 위 표는 reverse process가 길수록 FID 점수가 높아지는 것을 보여주며, 이는 $t$ 값이 클수록 더 큰 오차 누적이 있음을 나타낸다.
Method
1. Regularization with Input Perturbation
본 논문이 exposure bias 문제를 완화하기 위해 제안하는 솔루션은 매우 간단하다. 학습 시에 가우시안 입력 섭동을 사용하여 예측 오차를 명시적으로 모델링한다. 보다 구체적으로, 시간 $t+1$에서 reverse process에서 예측 네트워크의 오차가 ground-truth 입력 $x_t$에 대해 정규 분포라고 가정한다. 이것은 두 번째 랜덤 noise 벡터 $\xi \sim \mathcal{N}(0, I)$을 사용하여 시뮬레이션되며, 이를 사용하여 $x_t$의 섭동 버전 $y_t$을 생성한다.
\[\begin{equation} y_t = \sqrt{\vphantom{1} \bar{\alpha}_t} x_0 + \sqrt{1 - \bar{\alpha}_t} (\epsilon + \gamma_t \xi) \end{equation}\]단순화를 위해 $\gamma_0 = \cdots = \gamma_T = \gamma$로 설정하여 $\xi$에 대해 균일한 noise schedule을 사용한다. 실제로 DDPM에서 최상의 noise schedule $(\beta_1, \cdots, \beta_T)$을 선택하는 것은 일반적으로 고품질 결과를 얻는 데 매우 중요하지만 그럼에도 불구하고 비용이 많이 드는 hyperparameter 튜닝 작업이다. 따라서 저자들은 학습 절차에 두 번째 noise schedule $(\gamma_0, \cdots, \gamma_T)$를 추가하지 않기 위해 $\gamma_t$가 $t$에 따라 변하지 않는 더 간단한 (비록 최적이 아닐 가능성이 높지만) 솔루션을 선택했다. Algorithm 3에서는 $x_t$가 $y_t$로 대체되는 제안된 학습 알고리즘을 보여준다. 반대로 inference 시에는 Algorithm 2를 변경 없이 사용한다.

Discussion
Algorithm 3의 line 5에서 예측 네트워크 $\epsilon_\theta$의 입력으로 $y_t$를 사용하지만 회귀 대상으로 $\epsilon$를 계속 사용한다. 즉, 도입하는 새로운 noise 항 $\xi$는 입력에 적용되지만 예측 대상 $\epsilon$에는 적용되지 않기 때문에 비대칭적으로 사용된다. 이러한 이유로 Algorithm 3은 Algorithm 1에서 $\epsilon$의 다른 값을 선택하는 것과 동일하지 않다. $\epsilon$은 forward process와 예측 네트워크의 대상으로 대칭적으로 사용된다.
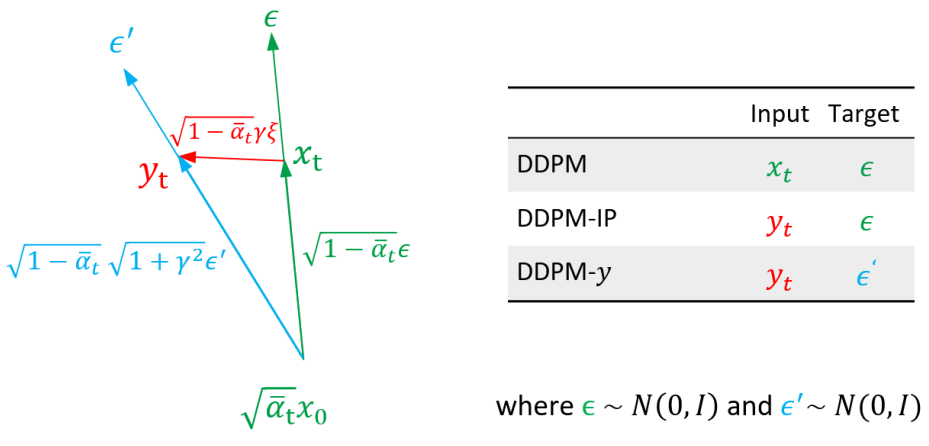
이 차이는 위 그림에 개략적으로 설명되어 있다. 여기서 Algorithm 1 (DDPM)과 Algorithm 3 (DDPM-IP) 모두에 대해 예측 네트워크의 해당 입력과 타겟 벡터 쌍 $(x_t, \epsilon)$과 $(y_t, \epsilon)$을 보여준다. 같은 그림에서 Algorithm 1을 사용하지만 $y_t$를 생성하는 동일한 분포를 고수하기 위해 noise 분산을 변경하는 Algorithm 1 (DDPM-y)의 두 번째 버전도 보여준다. 실제로 Algorithm 3의 $y_t$가 다음 분포를 사용하여 생성됨을 쉽게 알 수 있다.
따라서 $\epsilon’ \sim \mathcal{N}(0, I)$를 사용하여 Algorithm 1에서 Algorithm 3의 동일한 입력 noise 분포를 얻을 수 있다.
\[\begin{equation} y_t = \sqrt{\vphantom{1} \bar{\alpha}_t} x_0 + \sqrt{1 - \bar{\alpha}_t} \sqrt{1 + \gamma^2} \epsilon' \end{equation}\]이 새로운 noise 분포를 사용한 버전을 DDPM-y라고 한다. DDPM-y는 line 3에서 위 식을 사용하고 line 4에서 $x_t$를 $y_t$로, $\epsilon$를 $\epsilon’$로 대체하여 Algorithm 1에서 얻는다. 그러나 주어진 $y_t$에 대해 $\xi \ne 0$0이면 $\epsilon \ne \epsilon’$이므로 DDPM-IP과 DDPM-y는 $\epsilon_\theta$에 대해 동일한 입력을 공유하지만 서로 다른 타겟을 사용한다.
직관적으로, DDPM-IP는 $\epsilon_\theta$에 의해 예측되도록 요청된 ground-truth 타겟 벡터 $\epsilon$에서 실제로 $y_t$를 생성하는 noise 벡터 $\epsilon’$를 분리한다. 이 문제를 해결하기 위해 $\epsilon_\theta$는 예측 함수를 매끄럽게하여 $\epsilon_\theta (x_t, t)$와 $\epsilon_\theta (y_t, t)$의 차이를 줄여야 하며 이는 VRM과 유사한 학습 정규화로 이어진다.
3. Estimating the Prediction Error
저자들은 $\epsilon_\theta$의 실제 예측 오차를 분석하고 이 분석을 사용하여 $\gamma$의 값을 선택한다. 표준 알고리즘 Algorithm 1과 두 개의 데이터셋 CIFAR10과 ImageNet 32$\times$32를 사용하여 학습된 ADM을 사용한다. 테스트 시에 주어진 $t$와 \(\hat{\epsilon} = \epsilon_\theta (\hat{x}_t, t)\)에 대해 $\epsilon$를 \(\hat{\epsilon}\)로 대체하고 예측된 \(\hat{x}_0\)을 계산한다. 마지막으로 시간 $t$에서의 예측 오차는 \(e_t = \hat{x}_0 − x_0\)이다. \(\hat{x}_t\)와 $x_t$를 비교하는 대신 \(\hat{x}_0\)와 $x_0$를 사용하여 오차를 추정하는 것은 scaling factor $\sqrt{1 - \bar{\alpha}_t}$와 무관하다는 이점이 있으므로 통계 분석을 더 쉽게 만든다. \(\{1, \cdots, T\}\)에서 균일하게 선택된 $t$의 다양한 값을 사용하여 주어진 $t$에 대해 $e_t$가 $\mathcal{N}(0, \nu_t^2 I)$로 정규 분포됨을 경험적으로 확인했다.
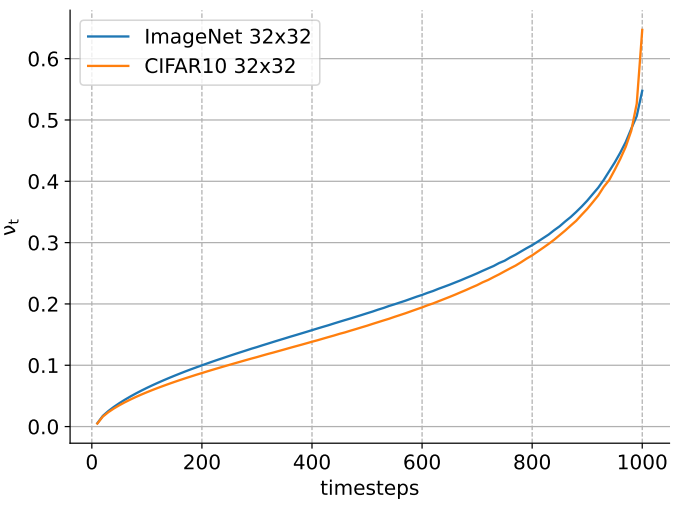
위 그림은 $t$에 대한 $\nu_t$의 값을 플로팅한 것이다. 두 데이터셋에 해당하는 두 곡선은 놀라울 정도로 서로 가깝다. 원칙적으로, 이 경험적 분석을 사용하여 $\gamma_t = \nu_t$로 설정할 수 있다. 이와 같이 $\epsilon_\theta$에 대한 입력을 섭동시키면 exposure bias 문제의 기반이 되는 실제 예측 오차를 경험적으로 모방한다.
그러나 이 선택에는 2단계 학습이 필요하다. 먼저 Algorithm 1을 사용하여 기본 모델을 학습시키고 여러 $t$에 대한 $\nu_t$를 경험적으로 추정한다. 그런 다음 추정된 $\gamma_t$ schedule과 함께 Algorithm 3을 사용하여 처음부터 모델을 재학습한다. 이를 피하고 전체 절차를 가능한 한 간단하게 만들기 위해 단순히 $t$와 독립적으로 상수 값 $\gamma$를 사용한다. 이 값은 샘플링 궤적의 마지막 절반을 포함하는 작은 범위의 값에 대해 CIFAR10과 ImageNet 32$\times$32 모두에서 그리드 grid search를 사용하여 경험적으로 설정되었다.
구체적으로 저자들은 범위 $\nu_t \in [0, \mathbb{E}_t [\nu_t]] = [0, 0.2]$를 조사했다. Inference 궤적의 마지막 부분은 일반적으로 diffusion model 성능에 가장 큰 영향을 미치기 때문이다. $\gamma = 0.1$로 설정하고 본 논문의 나머지 부분에서는 데이터셋과 기준 DDPM에 관계없이 항상 상수 $\gamma = 0.1$을 사용한다. 각 DDPM 전용의 $\gamma$ 값이 더 나은 품질 결과로 이어질 가능성이 높지만 저자들은 다른 hyperparameter에 의존하지 않는 사용 용이성을 강조하는 것을 선호하였다.
4. Regularization based on Lipschitz Continuous Functions
본 논문은 현상을 더 잘 조사하는 데 도움이 될 수 있는 exposure bias 문제에 대한 두 가지 대안 솔루션을 제안한다. 목표는 예측 함수 $\epsilon_\theta (x_t, t)$를 매끄럽게하여 inference 예측 오차로 인한 $x_t$의 로컬 변동에 대해 더 견고하게 만드는 것이다. 이를 위해 입력 섭동을 사용하는 대신 명시적으로 $\epsilon_\theta$가 Lipschitz 연속이 되도록 권장한다. 즉, 작은 상수 $K$에 대해 다음을 충족한다.
\[\begin{equation} \| \epsilon_\theta (x, t) - \epsilon_\theta (y, t) \| \le K \| x- y \|, \quad \forall (x, y) \end{equation}\]저자들은 두 가지 표준 Lipschitz 상수 최소화 방법인 gradient penalty와 weight decay를 사용하여 이 아이디어를 구현하였다. 두 경우 모두 $\epsilon_\theta$의 입력을 섭동시키지 않고 Algorithm 1을 사용한다. 유일한 차이점은 L2 loss가 정규화 항과 함께 사용되는 loss function이다.
Gradient penalty
이 경우 정규화는 Jacobian 행렬의 Frobenius norm을 기반으로 하며 최종 loss는 다음과 같다.
\[\begin{equation} L_\textrm{GP} (\theta) = \| \epsilon - \epsilon_\theta (x_t, t) \|^2 + \lambda_\textrm{GP} \bigg\| \frac{\partial \epsilon_\theta (x_t, t)}{\partial x} \bigg\|_F^2 \end{equation}\]여기서 $\lambda_\textrm{GP}$는 gradient penalty 항의 가중치이다. 그러나 gradient penalty 정규화는 각 학습 step에 대해 하나의 forward pass와 2개의 backward pass를 포함하기 때문에 매우 느리다.
Weight decay
Lipschitz 연속성은 weight decay 정규화를 사용하여 권장할 수도 있다. 이 경우 최종 loss는 다음과 같다.
\[\begin{equation} L_\textrm{WD} (\theta) = \| \epsilon - \epsilon_\theta (x_t, t) \|^2 + \lambda_\textrm{WD} \| \theta \|^2 \end{equation}\]여기서 $\lambda_\textrm{WD}$는 정규화 항의 가중치이다.
Results
1. Evaluation of the Different Proposed Solutions
다음은 다양한 정규화 방법을 비교한 표이다.

2. Main results
Comparison with DDPMs
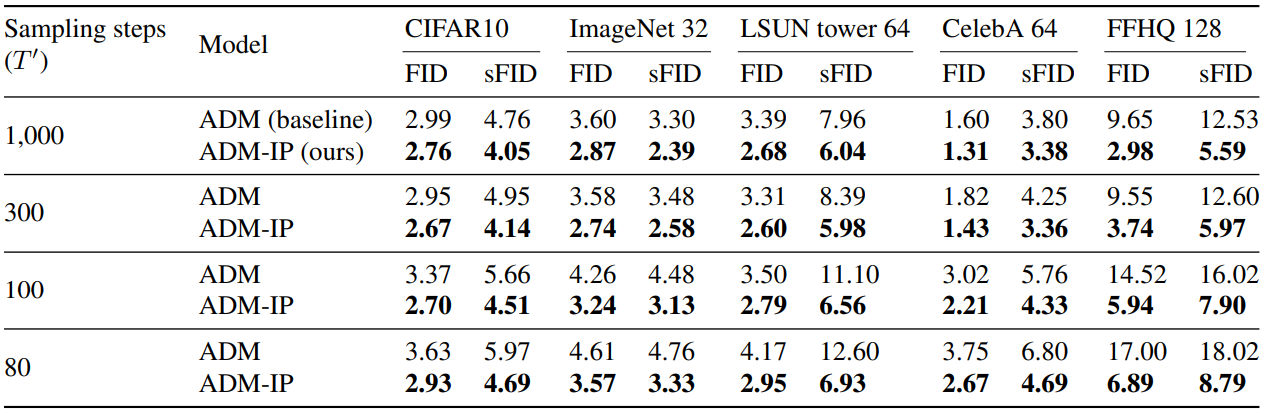
다음은 여러 $T’ \le T$에서 $T = 1000$으로 학습된 ADM과 ADM-IP를 비교한 표이다.
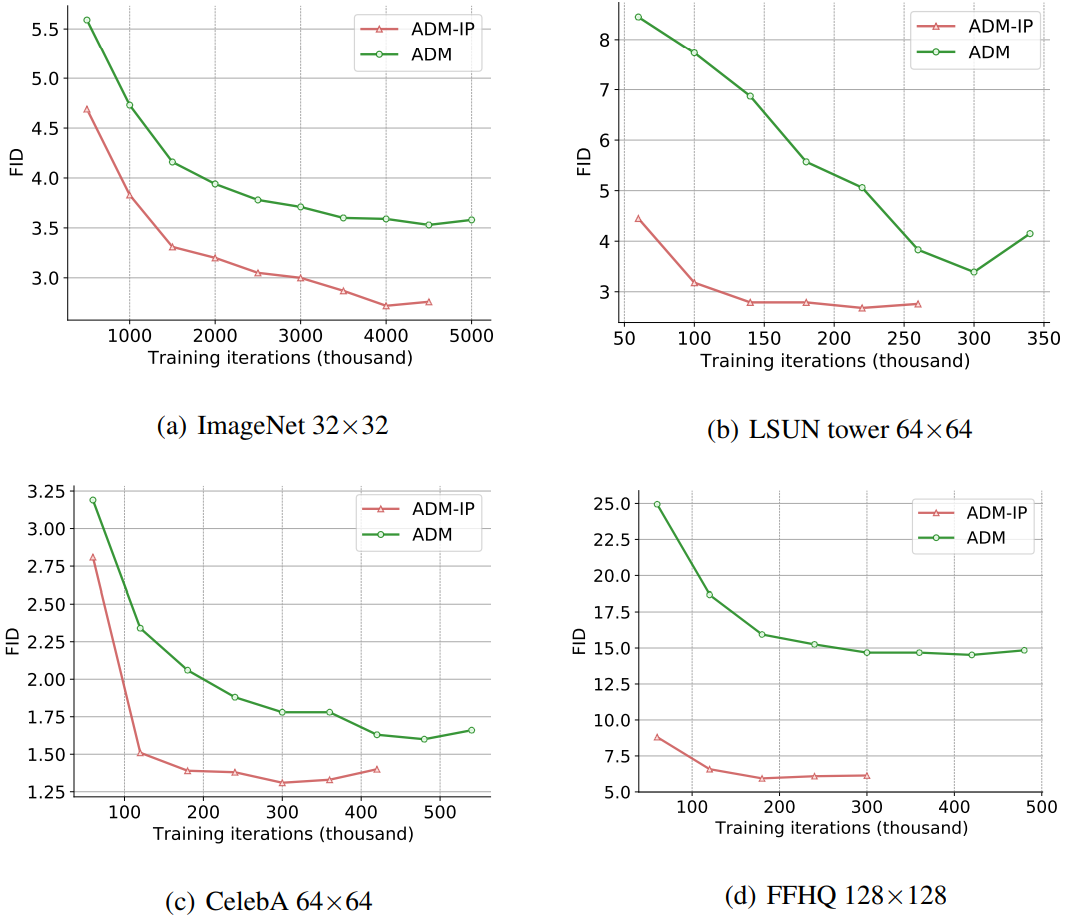
다음은 학습 iteration 수에 따른 FID 점수를 비교한 그래프이다. FFHQ에서는 $T’ = 100$이고 다른 데이터셋에서는 $T’ = 1000$이다.
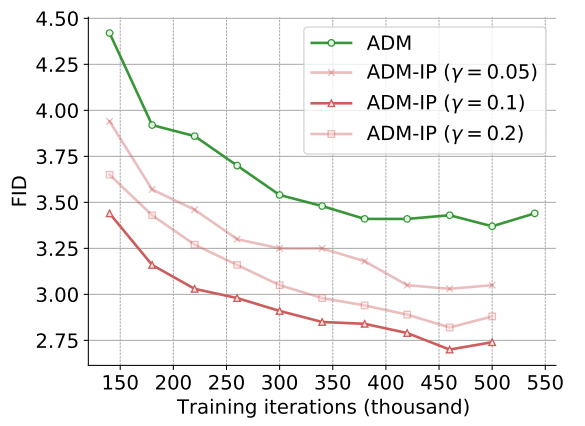
다음은 다양한 $\gamma$ 값에 따른 FID 점수를 학습 iteration 수에 대하여 나타낸 그래프이다.
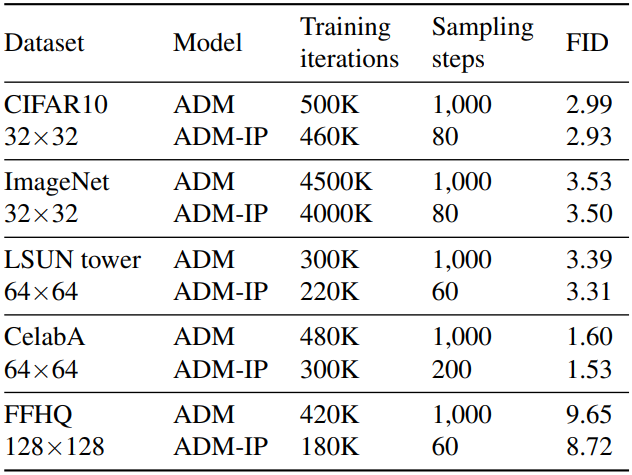
다음은 각 모델이 수렴할 때까지 학습하였을 때의 성능을 비교한 표이다.
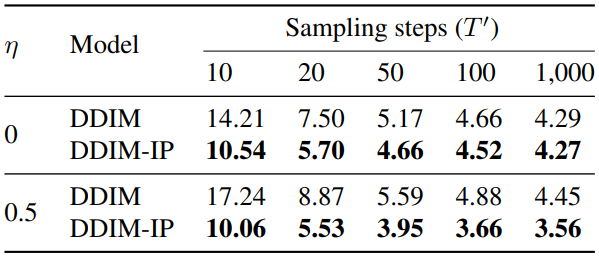
Comparison with DDIMs
다음은 여러 $T’ \le T$에서 $T = 1000$으로 학습된 DDIM과 DDIM-IP를 비교한 표이다.
Limitations
DDPM 학습은 계산량이 매우 많기 때문에 본 논문에서는 해상도가 작은 이미지가 있는 데이터셋만 사용했다.