[논문리뷰] An Edit Friendly DDPM Noise Space: Inversion and Manipulations

CVPR 2024. [Paper] [Page] [Github]
Inbar Huberman-Spiegelglas, Vladimir Kulikov, Tomer Michaeli
Technion
12 Apr 2023

Introduction

Diffusion model은 이미지 합성에서 SOTA 품질을 달성하는 강력한 생성 프레임워크로 등장했다. 최근 연구들에서는 텍스트 기반 편집, 인페인팅, image-to-image translation을 포함한 다양한 이미지 편집 작업에 diffusion model을 활용하였다. 이러한 방법들의 주요 과제는 모델이 생성한 이미지가 아닌 실제 콘텐츠 편집에 이를 활용하는 것이다. 이를 위해서는 생성 프로세스를 반전(inversion)시켜야 한다. 즉, reverse process를 구동하는 데 사용되는 경우 주어진 이미지를 재구성하는 일련의 noise 벡터를 추출해야 한다.

Diffusion 기반 편집의 상당한 발전에도 불구하고 inversion은 특히 DDPM 샘플링 방식에서 여전히 주요 과제로 간주된다. 최근의 많은 방법들은 하나의 초기 noise 벡터를 생성된 이미지에 매핑하는 deterministic한 샘플링 프로세스인 DDIM 방식에 대한 근사 inversion 방법에 의존한다. 그러나 이 DDIM inversion 방법은 많은 수의 diffusion timestep (ex. 1000)를 사용할 때만 정확해지며, 이 방식에서도 종종 텍스트 기반 편집에서 좋지 못한 결과로 이어진다. 이 효과에 맞서기 위해 일부 방법들은 주어진 이미지와 텍스트 프롬프트를 기반으로 diffusion model을 fine-tuning하였다. 다른 방법들은 다양한 방식으로, 예를 들어 DDIM inversion 프로세스에서 파생된 attention map을 텍스트 기반 생성 프로세스에 주입하여 생성 프로세스를 방해한다.

본 논문에서는 DDPM을 반전시키는 문제를 해결하였다. DDIM과 달리 DDPM에서는 $T + 1$개의 noise map이 생성 프로세스에 포함되며, 각각은 생성된 출력과 동일한 차원을 갖는다. 따라서 noise 공간의 전체 크기는 출력의 크기보다 크고 이미지를 완벽하게 재구성하는 noise 시퀀스는 무한히 많이 존재한다. 이 속성은 inversion 프로세스에 유연성을 제공할 수 있지만 모든 완벽한 재구성으로 이어지는 inversion이 편집 친화적인 것은 아니다. 예를 들어, 텍스트 조건부 모델의 맥락에서 noise map을 수정하고 텍스트 프롬프트를 변경하면 아티팩트 없는 이미지로 이어질 수 있어야 한다. 여기서 의미는 새 텍스트에 해당하지만 구조는 입력 이미지의 구조와 유사하게 유지된다. 이 속성을 만족시키는 일관된 inversion은 무엇인가? 유혹적인 대답은 노이즈 맵이 통계적으로 독립적이어야 하며 정규 샘플링과 같이 표준 정규 분포를 가져야 한다는 것이다. 그러나 이 기본 DDPM noise 공간은 실제로 편집 친화적이지 않다.

본 논문에서는 편집에 더 적합한 대체 inversion 방법을 제시하였다. 핵심 아이디어는 이미지를 noise map에 더 강하게 “각인”하여 이미지를 수정하고 모델 조건을 변경할 때 구조를 더 잘 보존하는 것이다. 특히 본 논문의 noise map은 기본 noise map보다 분산이 더 높으며 timestep에 걸쳐 강한 상관 관계가 있다. 중요한 점은 inversion이 최적화가 필요하지 않으며 속도가 매우 빠르다는 것이다. 그러나 간단히 noise map을 수정하고 텍스트 조건을 변경함으로써 (즉, 모델 fine-tuning 없이) 상대적으로 적은 수의 diffusion step으로 텍스트 기반 편집 작업에서 SOTA 결과를 얻을 수 있다. 본 논문의 DDPM inversion은 현재 대략적인 DDIM inversion에 의존하는 기존 diffusion 기반 편집 방법과 쉽게 통합될 수도 있다. 이는 원본 이미지에 대한 충실도를 유지하는 능력을 향상시킨다. 또한 확률론적 방식으로 noise 벡터를 찾기 때문에 텍스트 프롬프트를 모두 준수하는 다양한 편집 이미지들을 제공할 수 있다. 이는 DDIM inversion에서는 사용할 수 없는 속성이다.

The DDPM noise space

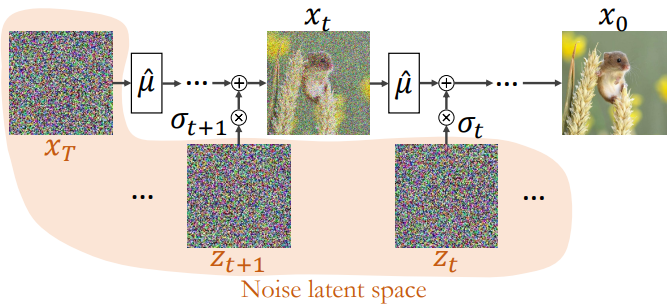
본 논문은 픽셀 공간과 latent 공간 모두에 적용할 수 있는 DDPM 샘플링 방식에 중점을 두었다. DDPM은 깨끗한 이미지 $x_0$를 Gaussian noise로 점진적으로 바꾸는 diffusion process를 역전시키려고 시도하여 샘플을 추출한다.

\[\begin{equation} x_t = \sqrt{1 - \beta_t} x_{t-1} + \sqrt{\beta_t} n_t, \quad t = 1, \ldots, T \end{equation}\]

여기서 \(\{n_t\}\)는 정규 분포 벡터이고 \(\{\beta_t\}\)는 variance schedule이다. 이 diffusion process는 다음과 같이 등가적으로 표현된다.

\[\begin{equation} x_t = \sqrt{\vphantom{1} \bar{\alpha}_t} x_0 + \sqrt{1 - \bar{\alpha}_t} \epsilon_t \\ \quad \alpha_t = 1 - \beta_t, \; \bar{\alpha}_t = \prod_{s=1}^t \alpha_s, \; \epsilon_t \sim \mathcal{N} (0, \mathbf{I}) \end{equation}\]

위 식에서 벡터 \(\{\epsilon_t\}\)는 독립적이지 않다는 점이 중요하다. 실제로 모든 $t$에서 $\epsilon_t$와 \(\epsilon_{t-1}\)는 높은 상관 관계를 갖는다. 이는 학습 프로세스와는 관련이 없지만 inversion에서는 중요하다.

생성 프로세스(reverse process)는 랜덤 noise 벡터 $x_T \sim \mathcal{N}(0, I)$에서 시작하고 반복적으로 noise를 제거한다.

\[\begin{equation} x_{t-1} = \hat{\mu}_t (x_t) + \sigma_t z_t, \quad t = T, \ldots, 1 \end{equation}\]

여기서 \(\{z_t\}\)는 정규 분포 벡터이고, \(\hat{\mu}_t (x_t)\)는 다음과 같다.

\[\begin{equation} \hat{\mu}_t (x_t) = \sqrt{\vphantom{1} \bar{\alpha}_{t-1}} P(f_t (x_t)) + D (f_t (x_t)) \\ \textrm{where} \quad P(f_t (x_t)) = \frac{x_t - \sqrt{1 - \bar{\alpha}_t} f_t (x_t)}{\sqrt{\vphantom{1} \bar{\alpha}_t}}, \quad D(f_t (x_t)) = \sqrt{1 - \bar{\alpha}_{t-1} - \sigma_t^2} f_t (x_t) \end{equation}\]

여기서 $f_t (x_t)$는 $x_t$에서 $\epsilon_t$를 예측하도록 학습된 신경망이다. $P(f_t (x_t))$는 예측된 $x_0$이며, $D(f_t (x_t))$는 $x_t$를 가리키는 방향이다. Variance schedule은 다음과 같이 표현할 수 있다.

\[\begin{equation} \sigma_t = \eta \beta_t \frac{1 - \bar{\alpha}_{t-1}}{1 - \bar{\alpha}_t}, \quad \eta \in [0, 1] \end{equation}\]

$\eta = 1$인 경우는 DDPM에 해당하고 $\eta = 0$은 deterministic한 DDIM에 해당한다. 이 생성 프로세스는 입력에 대해 학습된 신경망 $f$를 사용하여 텍스트 또는 클래스로 컨디셔닝될 수 있다. 또는 생성 프로세스에서 사전 학습된 classifier 또는 CLIP 모델을 활용해야 하는 guided diffusion을 통해 컨디셔닝할 수 있다.

벡터 \(\{x_T, z_T, \ldots, z_1\}\)은 생성 프로세스에 의해 생성된 이미지 $x_0$를 고유하게 결정한다 (그 반대는 아님). 그러므로 그것들을 모델의 latent code로 간주한다. 여기서 본 논문은 반대 방향에 관심이 있다. 즉, 실제 이미지 $x_0$가 주어지면 $x_0$를 생성하는 noise 벡터를 추출하려고 하는 것이 목표이다.

Edit friendly inversion

$T + 1$개의 이미지의 시퀀스 $x_0, \ldots, x_T$는 실제 이미지 $x_0$에서 시작하여 $z_t$를 다음과 같이 분리하여 일관된 noise map을 추출하는 데 사용할 수 있다.

\[\begin{equation} z_t = \frac{x_{t-1} - \hat{\mu}_t (x_t)}{\sigma_t}, \quad t = T, \ldots, 1 \end{equation}\]

그러나 이러한 보조 이미지 시퀀스를 주의 깊게 구성하지 않으면 네트워크 $f_t$가 학습된 입력 분포와 매우 멀리 떨어져 있을 가능성이 높다. 이 경우 추출된 noise 맵을 수정하고 텍스트 조건을 변경하면 결과가 좋지 않을 수 있다.

보조 이미지 $x_1, \ldots, x_T$를 구성하는 좋은 방법은 무엇일까? 순진한 접근 방식은 생성 프로세스의 기본 분포와 유사한 분포에서 이를 추출하는 것이다. 구체적으로, $x_T \sim \mathcal{N} (0, \textbf{I})$를 샘플링하는 것으로 시작한다. 그런 다음 각 $t = T, \ldots, 1$에 대해 $x_t$와 $x_0$를 사용하여 $\epsilon_t$를 분리하고, $f_t (x_t)$ 대신 이 $\epsilon_t$를 대체하여 \(\hat{\mu}_t (x_t)\)를 계산하고, 이 \(\hat{\mu}_t (x_t)\)를 사용하여 $x_{t-1}$을 얻는다.

이 방법으로 추출된 noise map은 생성 프로세스의 noise map과 유사하게 분포된다. 그러나 불행히도 글로벌한 구조를 편집하는 데는 적합하지 않다. 그 이유는 애초에 DDPM의 기본 noise 공간이 편집 친화적이지 않기 때문이다. 즉, 모델이 생성한 이미지에서 ground-truth noise map을 얻더라도 텍스트 프롬프트를 변경하여 이미지를 수정하면 이미지의 구조가 보존되지 않는다.

여기서 저자들은 이미지 $x_0$ 내의 구조가 추출된 noise map에 더 강하게 “각인”되도록 보조 시퀀스 $x_1, \ldots, x_T$를 구성할 것을 제안하였다. 구체적으로 다음과 같이 구성한다.

\[\begin{equation} x_t = \sqrt{\vphantom{1} \bar{\alpha}_t} x_0 + \sqrt{1 - \bar{\alpha}_t} \tilde{\epsilon}_t, \quad t = 1, \ldots, T \end{equation}\]

여기서 \(\tilde{\epsilon}_t \sim \mathcal{N}(0,\textbf{I})\)는 통계적으로 독립적이다. 이 식과 diffusion process 사이의 표면적인 유사성에도 불구하고 둘은 근본적으로 다른 확률론적 프로세스를 설명한다. Diffusion process에서 연속적인 $\epsilon_t$의 모든 쌍은 높은 상관관계를 갖고 있는 반면, 위 식에서 \(\tilde{\epsilon}_t\)는 독립적이다. 이는 제안된 구성에서 $x_t$와 $x_{t−1}$이 일반적으로 diffusion process보다 서로 더 멀리 떨어져 있으므로 추출된 모든 $z_t$가 일반 생성 프로세스보다 더 높은 분산을 가질 것으로 예상됨을 의미한다. 이 방법의 pseudo-code는 Algorithm 1에 요약되어 있다.

이 inversion 방법은 몇 가지 특징이 있다.

1. 수치적 오차의 누적을 보상한다는 점을 고려하여 입력 이미지를 machine epsilon (부동소수점 연산에서 반올림을 함으로써 발생하는 오차의 상한)까지 재구성한다.
2. \(\hat{\mu}_t\)에 적합한 형식을 사용하면 모든 종류의 diffusion process(ex. 조건부 모델, guided diffusion, classifier-free)와 함께 사용하는 것이 간단하다.
3. 식의 무작위성으로 인해 다양한 inversion을 얻을 수 있다. 각각은 완벽한 재구성으로 이어지지만 편집에 사용되면 편집된 이미지의 다양한 변형으로 이어진다. 이를 통해 결과의 다양성을 생기며, 이는 DDIM inversion에서는 사용할 수 없는 능력이다.

Properties of the edit-friendly noise space

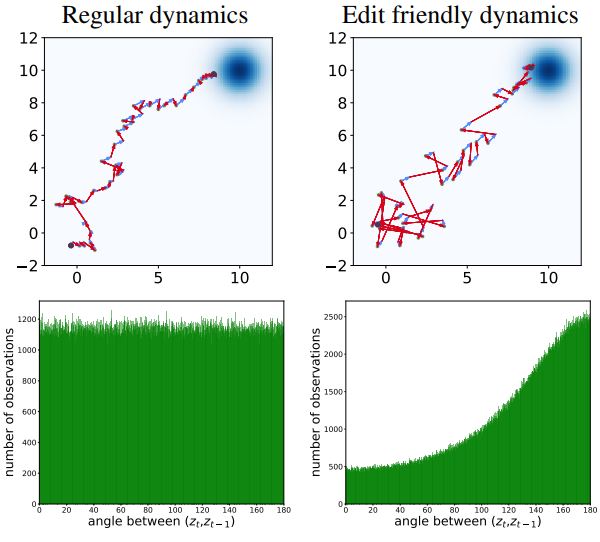
이제 편집 친화적인 noise 공간의 속성을 탐색하고 이를 기본 DDPM noise 공간과 비교하자. 위 그림에 표시된 2D 그림에서 시작하자. 여기서는 $\mathcal{N}((10, 10), \textbf{I})$에서 샘플링하도록 설계된 diffusion model을 사용한다. 왼쪽 위는 inference step이 40개인 일반 DDPM 프로세스이다. 왼쪽 하단의 $x_T \sim \mathcal{N} ((0, 0), \textbf{I})$에서 시작하여 오른쪽 상단의 $x_0$로 끝나는 시퀀스 \(\{x_t\}\)를 생성한다. 각 step은 deterministic drift \(\hat{\mu}_t (x_t)\)(파란색 화살표)와 noise 벡터 $z_t$(빨간색 화살표)로 분류된다. 오른쪽 위는 latent space에 대한 것이다. 여기서는 Algorithm 1을 사용하여 주어진 $x_0 \sim \mathcal{N}((10, 10), \textbf{I})$에서 \(\{x_t\}\)와 \(\{z_t\}\)를 계산한다.

위 그림에서 볼 수 있듯이, 본 논문의 방법을 사용하면 noise \(\{z_t\}\)가 더 크다. 또한 연속적인 noise 벡터 사이의 각도가 둔해지는 경향이 있다. 즉, noise 벡터는 연속적인 시간에 걸쳐 음의 상관 관계를 갖는다. 이는 일반 샘플링 프로세스와 본 논문의 프로세스에 대한 연속되는 noise 벡터 사이의 각도 히스토그램에서도 볼 수 있다. 일반 샘플링 프로세스의 경우 각도 분포가 균일하고, 본 논문의 프로세스의 경우 180도에서 피크를 갖는다.

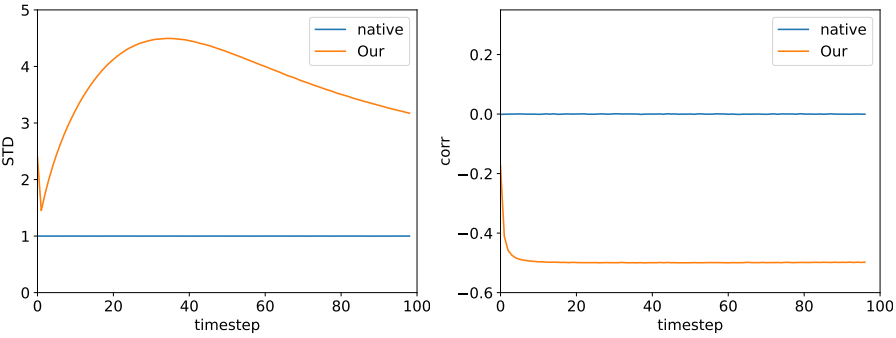
이미지 생성을 위한 diffusion model에서도 동일한 정성적 동작이 발생한다. 위 그림은 Imagenet에서 학습된 unconditional diffusion model의 100 step 샘플링에 대한 $z_t$의 픽셀당 분산과 $z_t$와 $z_{t−1}$ 사이의 상관 관계를 보여준다. 여기서 통계는 모델에서 가져온 10개의 이미지에 대해 계산되었다. 2D 예시와 마찬가지로 noise 벡터의 분산이 더 높으며 연속되는 step 간에 음의 상관 관계를 나타낸다. 이러한 속성은 noise 벡터를 더욱 편집하기 쉽게 만든다.

Image shifting

직관적으로 이미지 이동은 latent code의 $T + 1$개의 맵을 모두 이동해야 한다. 위 그림은 모델이 생성한 이미지의 latent code를 다양한 양만큼 이동한 결과이다. 위 그림에서 볼 수 있듯이 기본 latent code (이미지 생성에 사용된 코드)를 이동하면 이미지 구조가 완전히 손실된다. 대조적으로, 편집 친화적인 코드를 변경하면 약간의 성능 저하만이 발생한다.

Color manipulations

또한 latent space는 편리한 색상 조작을 가능하게 한다. 구체적으로 입력 이미지 $x_0$, 바이너리 마스크 $B$, 컬러 마스크 $M$이 주어졌다고 가정하자. 먼저 \(\{x_1, \ldots, x_T\}\)와 \(\{z_1, \ldots, x_T\}\)를 계산한다. 그런 다음 noise map을 다음과 같이 수정한다.

\[\begin{equation} z_t^\textrm{edited} = z_t + sB \odot (M - P(f_t (x_t))) \end{equation}\]

여기서 $s$는 편집 강도를 제어하는 파라미터이다.

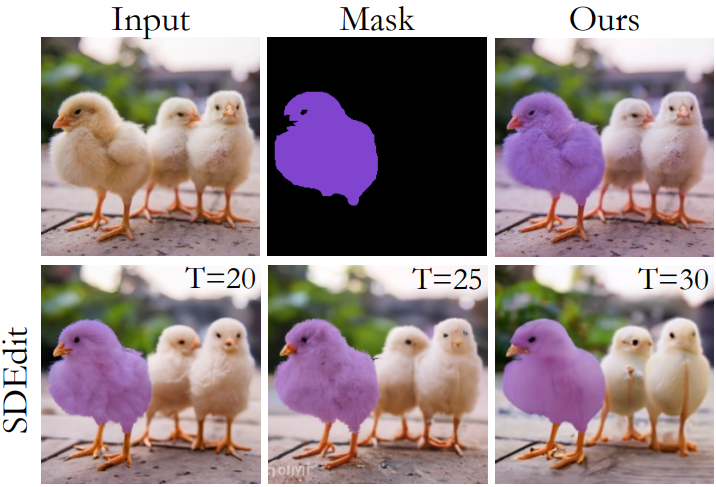
위 그림은 이 프로세스를 SDEdit과 비교한 결과이다. 본 논문의 접근 방식은 텍스처를 수정하지 않고도 강력한 편집 효과를 얻을 수 있다.

Text-Guided Image Editing

Latent space는 텍스트 기반 이미지 편집을 위해 더욱 활용될 수 있다. 실제 이미지 $x_0$, 이를 설명하는 텍스트 프롬프트 $p_\textrm{src}$ 및 대상 텍스트 프롬프트 $p_\textrm{tar}$이 주어졌다고 가정하자. 이러한 프롬프트에 따라 이미지를 수정하기 위해 $p_\textrm{src}$를 denoiser에 주입하는 동안 편집 친화적인 noise map \(\{x_T, z_T, \ldots, z_1\}\)을 추출한다. 그런 다음 noise map을 수정하고 $p_\textrm{tar}$를 denoiser에 주입하면서 이미지를 생성한다. Timestep $T - T_\textrm{skip}$부터 시작하여 생성 프로세스를 실행한다. 여기서 $T_\textrm{skip}$은 입력 이미지를 유지하는 정도를 제어하는 파라미터이다.

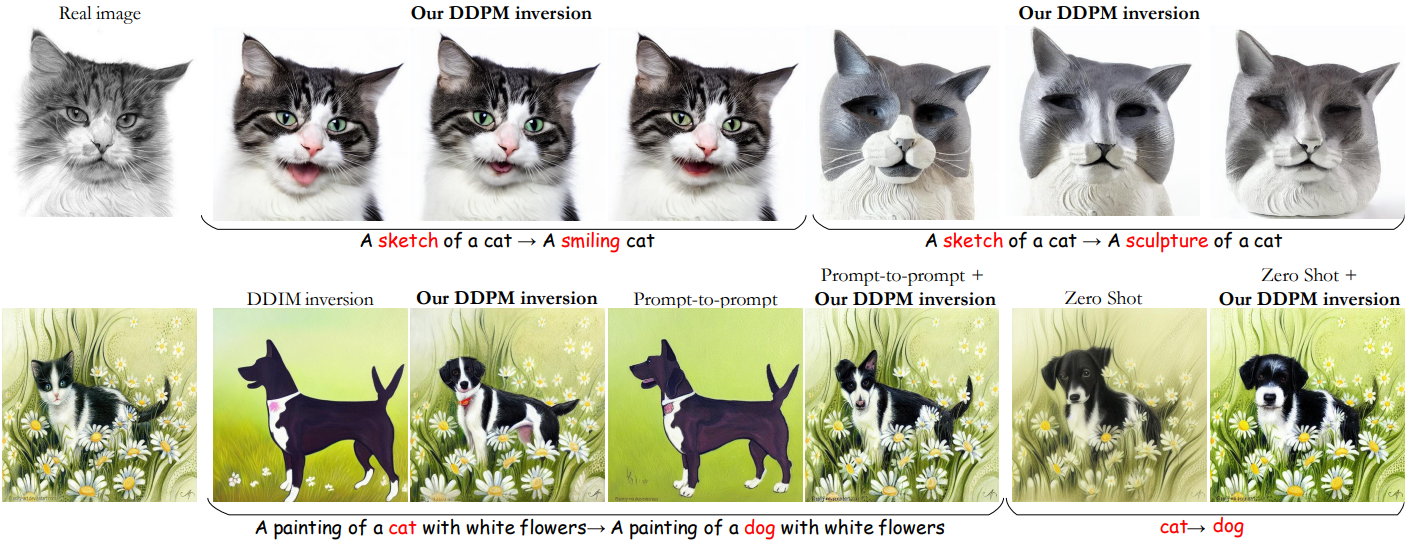
다음은 이 접근 방식을 사용한 텍스트 기반 편집 예시이다.

맨 왼쪽은 DDPM으로 샘플링한 이미지이며, 가운데는 기본 noise map, 오른쪽은 본 논문의 latent space이다. 첫번째 행은 텍스트 프롬프트를 변경한 것이고, 두번째 행과 세번째 행은 각각 noise map을 뒤집고 이동한 결과이다.

Experiments

다음은 수정된 ImageNet-R-TI2I 데이터셋에 대한 비교 결과이다. PnP는 Plug-and-Play Diffusion이고 P2P는 Prompt-to-Prompt이다.

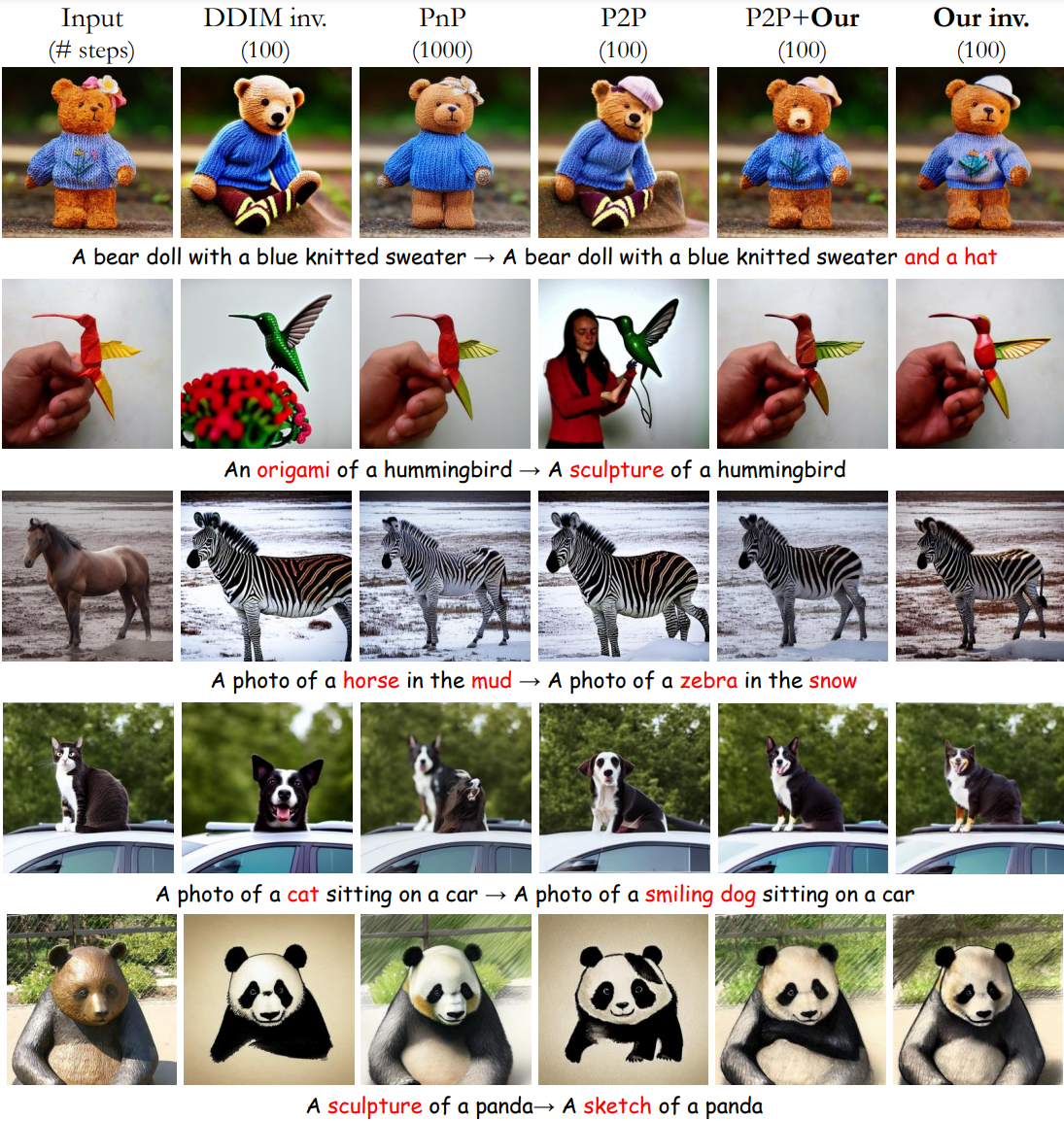
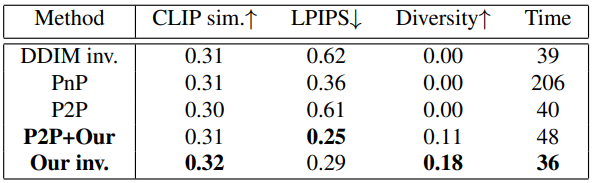
다음은 수정된 Zero-Shot I2IT 데이터셋에 대하여 pix2pix-zero와 비교 결과이다.