[논문리뷰] Zero-Shot Image Restoration Using Denoising Diffusion Null-Space Model (DDNM)

arXiv 2022. [Paper] [Github]
Yinhuai Wang, Jiwen Yu, Jian Zhang
Peking University Shenzhen Graduate School | Peng Cheng Laboratory
1 Dec 2022

Introduction

Image Restoration (IR)는 원본 이미지 $x$와 비선형 noise $n$에 대하여 degrade된 이미지 $y = Ax + n$에서 고품질 이미지 $\hat{x}$를 얻어내는 것이 목표이다. $A$는 알려진 선형 연산자이며, 이미지 super-resolution에서 bicubic downsampler와 같은 것이다. 기존 IR 방법은 일반적으로 모델 기반으로 다음과 같은 해를 갖는다.

\[\begin{equation} \hat{x} = \underset{x}{\arg \min} \frac{1}{2 \sigma^2} \| Ax - y \|_2^2 + \lambda \mathcal{R} (x) \end{equation}\]

첫번째 항은 데이터 일관성을 따라 결과를 최적화하고 두번째 항은 이미지 분포의 사전 지식으로 결과를 정규화한다. 직접 디자인한 사전 지식은 아티팩트를 방지할 수 있지만 현실적인 디테일을 가져오지 못한다.

심층 신경망 (DNN)의 등장은 IR task를 푸는 새로운 패턴을 가져왔다. 일반적으로 신경망의 파라미터 $\theta$를 최적화하여 end-to-end DNN $\mathcal{D}_\theta$를 학습시킨다.

\[\begin{equation} \underset{\theta}{\arg \min} \sum_{i=1}^N \| \mathcal{D}_\theta (y_i) - x_i \|_2^2 \end{equation}\]

End-to-end 학습 기반의 IR 방법은 $A$와 prior 항의 명시적인 모델링을 피하며 신경망에 대한 해석이 부족하다. 해석 가능한 DNN 구조를 탐색하는 연구가 있었지만 $y_i$를 $x_i$로 매핑하는 것을 학습하다보니 domain shift가 있으면 성능이 나쁘다. 같은 이유로 각 특정 task를 위해 전용 DNN을 학습시켜야 하므로 다양한 IR task를 푸는 것에 대한 일반화 능력과 유연성이 부족하다.

생성 모델의 발전은 end-to-end 학습 기반의 IR 방법은 사실적인 결과를 생성하도록 만들었다. 동시에 몇몇 연구에서 사전 학습된 생성 모델의 latent space를 활용하여 zero-shot 방법으로 IR task를 해결하는 시도가 있었다. 사전 학습된 생성 모델이 $\mathcal{G}$이고 latent code가 $w$이면 목적 함수는 다음과 같다.

\[\begin{equation} \underset{w}{\arg \min} \frac{1}{2 \sigma^2} \| A \mathcal{G} (w) - y \|_2^2 + \lambda \mathcal{R} (w) \end{equation}\]

하지만 이 방법은 종종 현실성과 데이터 일관성 사이에서 균형을 맞추는 데 어려움이 있다.

Range-Null space decomposition는 현실성과 데이터 일관성 사이의 관계에 대한 새로운 관점을 제공하였다. 데이터 일관성은 range-space contents에만 연관이 있으며 수치적으로 계산할 수 있다. 따라서 데이터 항이 강력하게 보장되므로 주요 문제는 결과가 현실성이 있도록 적절한 null-space contents를 찾는 것이다. Diffusion model은 생성 프로세스에서 명시적인 제어가 가능하므로 이상적인 null-space contents를 얻을 수 있는 이상적인 도구이다.

본 논문에서는 다양한 IR task에 대한 새로운 zero-shot 방법인 Denoising Diffusion Null-Space Model (DDNM)을 제안한다. Reverse diffusion sampling에서 null-space contents만을 정제하므로 본 논문의 방법은 현실적이고 데이터 일관성이 높은 결과를 내는 상용 diffusion model만이 필요하며, 추가 학습이나 최적화, 신경망 구조의 수정이 필요없다. 광범위한 실험에서 DDNM이 state-of-the-art zero-shot IR 방법보다 다양한 IR task에서 성능이 우수하였다.

저자들은 추가로 생성 품질이 향상되고 noisy한 IR task를 해결할 수 있는 버전인 DDNM+를 제안한다. 본 논문의 방법들은 degradation mode의 domain shift에서 자유롭기 때문에 사진 복원과 같은 현실의 복잡한 IR task를 유연하게 해결할 수 있다.

Method

1. Denoising Diffusion Null-Space Model

Null-Space Is All We Need

다음과 같은 noise가 없는 IR에서 시작하자.

\[\begin{equation} y = Ax \end{equation}\]

$x \in \mathbb{R}^{D \times 1}$는 ground-truth (GT) 이미지, $A \in \mathbb{R}^{d \times D}$는 degradation 연산자, $y \in \mathbb{R}^{d \times 1}$는 degrade된 이미지이다. 입력 $y$가 주어지면 IR 문제는 2가지 제약조건을 만족하는 이미지 $\hat{x} \in \mathbb{R}^{D \times 1}$를 얻는 것이 목표이다.

\[\begin{equation} Consistency: \quad A \hat{x} \equiv y \\ Realness: \quad \hat{x} \sim q(x) \end{equation}\]

$q(x)$는 GT 이미지의 분포이다.

Consistency 제약조건은 range-null space decomposition에 의지할 수 있다. GT 이미지 $x$는 range-space 부분 $A^\dagger Ax$와 null-space 부분 $(I - A^\dagger A) x$로 분해될 수 있다. 놀라운 점은 연산 $A$를 하면 $A^\dagger Ax$는 정확히 $y$가 되고 $(I - A^\dagger A) x$는 정확히 0이 된다.

Consistency 제약조건을 만족하는 일반해 $\hat{x}$를

\[\begin{equation} \hat{x} = A^\dagger y + (I - A^\dagger A) \bar{x} \end{equation}\]

로 구성할 수 있으며, $\bar{x}$가 무엇이든 Consistency에 전혀 영향을 주지 않는다. 하지만 $\bar{x}$는 $\hat{x} \sim q(x)$인지를 결정한다. 그러면 $\hat{x} \sim q(x)$를 만족하는 적절한 $\bar{x}$를 찾는 것이 목표가 되며, 본 논문에서는 diffusion model를 사용하여 range-sapce $A^\dagger y$와 조화를 이루는 null-space $(I- A^\dagger A) \bar{x}$를 생성한다.

Refine Null-Space Iteratively

Reverse diffusion process는 반복적으로 $p(x_{t-1} \vert x_t, x_0)$에서 $x_{t-1}$을 샘플링하여 random noise $x_T \sim \mathcal{N}(0,I)$깨끗한 이미지 $x_0 \sim q(x)$를 얻는다. 하지만 이 프로세스는 완전히 랜덤하여 중간 state $x_t$가 noisy하다. Range-null space decomposition을 위한 깨끗한 중간 state를 얻기 위해 $p(x_{t-1} \vert x_t, x_0)$의 평균 $\mu_t (x_t, x_0)$와 분산 $\sigma_t^2$을 reparameterize한다.

\[\begin{equation} \mu_t (x_t, x_0) = \frac{\sqrt{\vphantom{1} \bar{\alpha}_{t-1}} \beta_t}{1 - \bar{\alpha}_t} x_0 + \frac{\sqrt{\alpha_t} (1 - \bar{\alpha}_{t-1})}{1 - \bar{\alpha}_t} x_t \\ \sigma_t^2 = \frac{1 - \bar{\alpha}_{t-1}}{1 - \bar{\alpha}_t} \beta_t \end{equation}\]

$x_0$를 모르지만 $q(x_t \vert x_0)$을 reverse하여 $x_t$와 예측된 noise $\epsilon_t = \mathcal{Z}\theta (x_t, t)$로 $x_0$를 추정할 수 있다. Timestep $t$에서 예측된 $x_0$를 $x{0 \vert t}$라고 하면 다음과 같다.

\[\begin{equation} x_{0 \vert t} = \frac{1}{\sqrt{\vphantom{1} \bar{\alpha}_t}} (x_t - \mathcal{Z}_\theta (x_t, t) \sqrt{1 - \bar{\alpha}_t}) \end{equation}\]

이 공식은 원래 DDPM과 동등하다. 마지막으로 $Ax_0 \equiv y$를 만족하는 $x_0$를 얻기 위해 range-space를 $A^\dagger y$로 고치고 null-space는 그대로 둔다. 그러면 수정된 추정 \(\hat{x}_{0 \vert t}\)를 다음과 같이 얻는다.

\[\begin{equation} \hat{x}_{0 \vert t} = A^\dagger y + (I - A^\dagger A) x_{0 \vert t} \end{equation}\]

따라서 \(\hat{x}_{0 \vert t}\)를 $x_0$로 사용하며, 이를 통해 null space만 reverse diffusion process에 참여하도록 만든다. 그런 다음 \(p(x_{t-1} \vert x_t, \hat{x}_{0 \vert t})\)에서 $x_{t-1}$을 얻는다

\[\begin{equation} x_{t-1} = \frac{\sqrt{\vphantom{1} \bar{\alpha}_{t-1}} \beta_t}{1 - \bar{\alpha}_t} \hat{x}_{0 \vert t} + \frac{\sqrt{\alpha_t} (1 - \bar{\alpha}_{t-1})}{1 - \bar{\alpha}_t} x_t + \sigma_t \epsilon \end{equation}\]

여기서 $\epsilon \sim \mathcal{N}(0,I)$이다. $x_{t-1}$은 \(\hat{x}_{0 \vert t}\)에 noise가 추가된 버전이며 추가된 noise는 range-space contents $A^\dagger y$와 null-space contents \((I - A^\dagger A) x_{0 \vert t}\) 사이의 불일치를 지운다. 반복적으로 위의 식들을 적용하면 최종 결과 $x_0 \sim q(x)$를 얻는다. 모든 수정된 추정 \(\hat{x}_{0 \vert t}\)은 Consistency 제약조건을 만족한다.

$x_0$가 \(\hat{x}_{0 \vert t}\)와 같다고 생각하므로 마지막 결과 $x_0$도 Consistency 제약조건을 만족한다. Denoising diffusion model을 null-space 정보를 채우는 데 사용하므로 제안된 방법을 Denoising Diffusion Null-Space Model (DDNM)라 부른다.

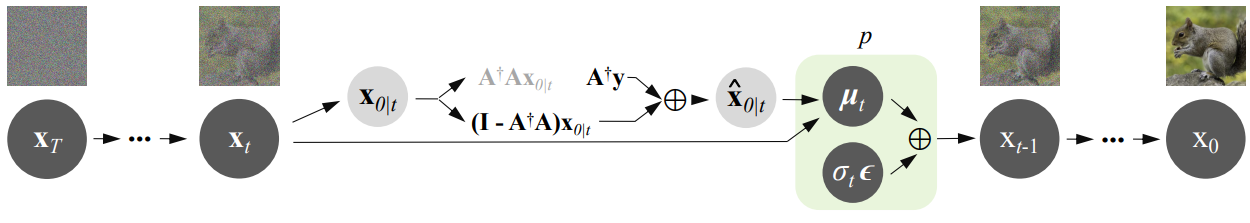
위의 Algorithm 1과 그림은 DDNM의 전체 reverse diffusion process를 보여준다. 일반적인 생성 목적으로 사전 학습된 $\mathcal{Z}_\theta$를 사용하여 DDNM은 임의의 형태의 $A$를 가진 IR task를 풀 수 있다. Task별 학습이나 최적화가 필요하지 않으며 다양한 IR task를 위한 zero-shot 해를 얻는다.

2. Enhanced version: DDNM+

DDNM은 noise가 없는 IR task를 잘 해결하지만 noisy한 IR task를 다루지 못하고 특정 형태의 $A^\dagger$에서 현실성이 떨어진다. 이 두 가지 한계를 극복하기 위하여 향상된 버젼인 DDNM+를 제안한다. DDNM+은 DDNM에 두가지 주요 확장을 추가하여 noisy한 상황을 다룰 수 있고 복구 품질을 개선한다. DDNM+을 알고리즘은 아래와 같다.

Scaling Range-Space Correction to Support Noisy Image Restoration

Noisy한 IR 문제 $y = Ax + n$를 생각해보자. $n \in \mathbb{R}^{d \times 1} \sim \mathcal{N} (0, \sigma_y^2 I)$는 추가 가우시안 noise이다. DDNM을 바로 적용하면

\[\begin{equation} \hat{x}_{0 \vert t} = A^\dagger y + (I - A^\dagger A) x_{0 \vert t} = x_{0 \vert t} - A^\dagger (A x_{0 \vert t} - Ax) + A^\dagger n \end{equation}\]

이며, $A^\dagger n \in \mathbb{R}^{D \times 1}$은 \(\hat{x}_{0 \vert t}\)에 들어가는 추가 noise이며 $x_{t-1}$에도 들어간다. \(A^\dagger (A x_{0 \vert t} - Ax)\)는 range-space contents를 위한 correction이다. 저자들은 noisy한 이미지를 복구하기 위해 다음과 같은 수정된 DDNM을 제안한다.

\[\begin{equation} \hat{x}_{0 \vert t} = x_{0 \vert t} - \Sigma_t A^\dagger (A x_{0 \vert t} - y) \\ \hat{p} (x_{t-1} \vert x_t, \hat{x}_{0 \vert t}) = \mathcal{N} (x_{t-1}; \mu_t (x_t, \hat{x}_{0 \vert t}), \Phi_t I) \end{equation}\]

$\Sigma_t \in \mathbb{R}^{D \times D}$는 range-space correction \(A^\dagger (A x_{0 \vert t} - y)\)를 스케일링하기 위해 활용되며, $\Phi_t \in \mathbb{R}^{D \times D}$는 추가 noise $\sigma_t \epsilon$를 스케일링하기 위해 사용된다. $\Sigma_t$와 $\Phi_t$의 선택은 2가지 규칙을 따른다.

1. $\Sigma_t$와 $\Phi_t$는 $x_{t-1}$의 전체 noise 분산을 보장해야 하며, 그래야 전체 noise는 $\mathcal{Z}_\theta$로 예측될 수 있고 제거될 수 있다.
2. Range-space correction \(A^\dagger (A x_{0 \vert t} - y)\)를 최대한 보존하도록 $\Sigma_t$는 $I$에 최대한 가까워야 하며, 그래야 Consistency가 최대화할 수 있다.

SR과 colorization의 경우 $A^\dagger$는 copy operation이다. 따라서 $A^\dagger n$은 Gaussian noise $\mathcal{N} (0, \sigma_y^2 I)$로 근사할 수 있고, $\Sigma_t = \lambda_t I$와 $\Phi_t = \gamma_t I$로 간단하게 나타낼 수 있다.

\[\begin{equation} x_{t-1} = \frac{\sqrt{\vphantom{1} \bar{\alpha}_{t-1}} \beta_t}{1 - \bar{\alpha}_t} \hat{x}_{0 \vert t} + \frac{\sqrt{\alpha_t} (1 - \bar{\alpha}_{t-1})}{1 - \bar{\alpha}_t} x_t + \sigma_t \epsilon \end{equation}\]

이므로, 첫번째 규칙은 다음과 동등하다.

\[\begin{equation} (a_t \lambda_t \sigma_y)^2 + \gamma_t = \sigma_t^2, \quad a_t = \frac{\sqrt{\vphantom{1} \bar{\alpha}_{t-1}} \beta_t}{1 - \bar{\alpha}_t} \end{equation}\]

두번째 규칙을 고려하여 다음과 같이 설정한다.

\[\begin{equation} \gamma_t = \sigma_t^2 - (a_t \lambda_t \sigma_y)^2 \\ \lambda_t = \begin{cases} 1, & \sigma_t \ge a_t \sigma_y \\ \sigma_t / a_t \sigma_y, & \sigma_t < a_t \sigma_y \end{cases} \end{equation}\]

위의 간단한 버전에서 더 나아가 $A^\dagger$의 일반적인 형태를 위한 더 정확한 형태는 다음과 같다.

\[\begin{equation} \Sigma_t = V \textrm{diag} \{\lambda_{t_1}, \cdots, \lambda_{t_D}\} V^T \\ \Phi_t = V \textrm{diag} \{\gamma_{t_1}, \cdots, \gamma_{t_D}\} V^T \end{equation}\]

여기서 $V$는 $A$의 SVD $A = U \Sigma V^T$에서 얻을 수 있다. 여기서 hyperparamter는 $\sigma_y$ 뿐이다. Non-Gaussian noise는 Gaussian noise로 근사할 수 있고, 그러므로 위와 동일한 방법을 사용할 수 있다.

Time-Travel For Better Restoration Quality

Large-scale average-pooling downsampler를 사용한 SR, 낮은 샘플링 비율의 compressed sensing(CS), 큰 마스크를 사용한 inpainting과 같이 특정 케이스에서 DDNM은 낮은 현실성을 보인다. 이 케이스들에서 range-space contents $A^\dagger y$는 reverse diffusion process를 guide하기 너무 로컬하여 글로벌하게 조화로운 결과를 얻지 못한다.

\[\begin{equation} \mu_t (x_t, x_0) = \frac{\sqrt{\vphantom{1} \bar{\alpha}_{t-1}} \beta_t}{1 - \bar{\alpha}_t} x_0 + \frac{\sqrt{\alpha_t} (1 - \bar{\alpha}_{t-1})}{1 - \bar{\alpha}_t} x_t \\ \sigma_t^2 = \frac{1 - \bar{\alpha}_{t-1}}{1 - \bar{\alpha}_t} \beta_t \end{equation}\]

위 식을 다시 보자. 사후 확률 분포 $p(x_{t-1} \vert x_t, x_0)$의 평균값 $\mu_t (x_t, x_0)$은 $x_0$의 정확한 추정에 의존한다. Timestep $t$에서 DDNM은 $x_0$의 추정으로 \(\hat{x}_{0 \vert t}\)를 사용하지만, 만일 range-space contents $A^\dagger y$가 너무 로컬하거나 고르지 않으면 \(\hat{x}_{0 \vert t}\)는 조화롭지 않은 null-space contents를 가질 수 있다.

이 부조화를 해결하기 위해 과거를 수정하기 위해 시간 여행을 할 수 있다. Timestep $t+l$로 간다면 미래의 추정 \(\hat{x}_{0 \vert t}\)를 사용하여 다음 state $x_{t+l-1}$을 얻을 수 있으며, 이는 \(\hat{x}_{0 \vert t+l}\)보다 더 정확할 것이다. Reparameterization에 의해 이 연산은 $q(x_{t+l-1} \vert x_{t-1})$에서 $x_{t+l-1}$에서 샘플링하는 것과 동등하다. 이와 같이 뒤로 갔다 앞으로 가는 시간 여행 전략은 일반적인 IR task들에서 글로벌한 조화를 개선한다.

먼저 $q(x_{t+1} \vert x_t)$에서 $x_{t+l}$을 샘플링한 다음, timestep $t+l$로 돌아가 $x_{t-1}$을 얻을 때까지 일반적인 DDNM 샘플링을 반복한다. 이 시간 여행 트릭은 아래 그림과 같이 설명할 수 있다.

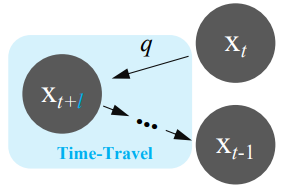
직관적으로, 시간 여행 트릭은 더 나은 과거를 생성하여 더 나은 미래를 생성한다. 이 트릭의 사용을 쉽게 하기 위해 추가로 2개의 hyperparamter를 할당한다.

1. $s$: 시간 여행 트릭을 사용할 간격
2. $r$: 반복 횟수

Experiments

1. Evaluation on DDNM

다음은 ImageNet(위)와 CelebA(아래)에 대한 zero-shot IR 방법의 정량적 결과를 나타낸 표이다.

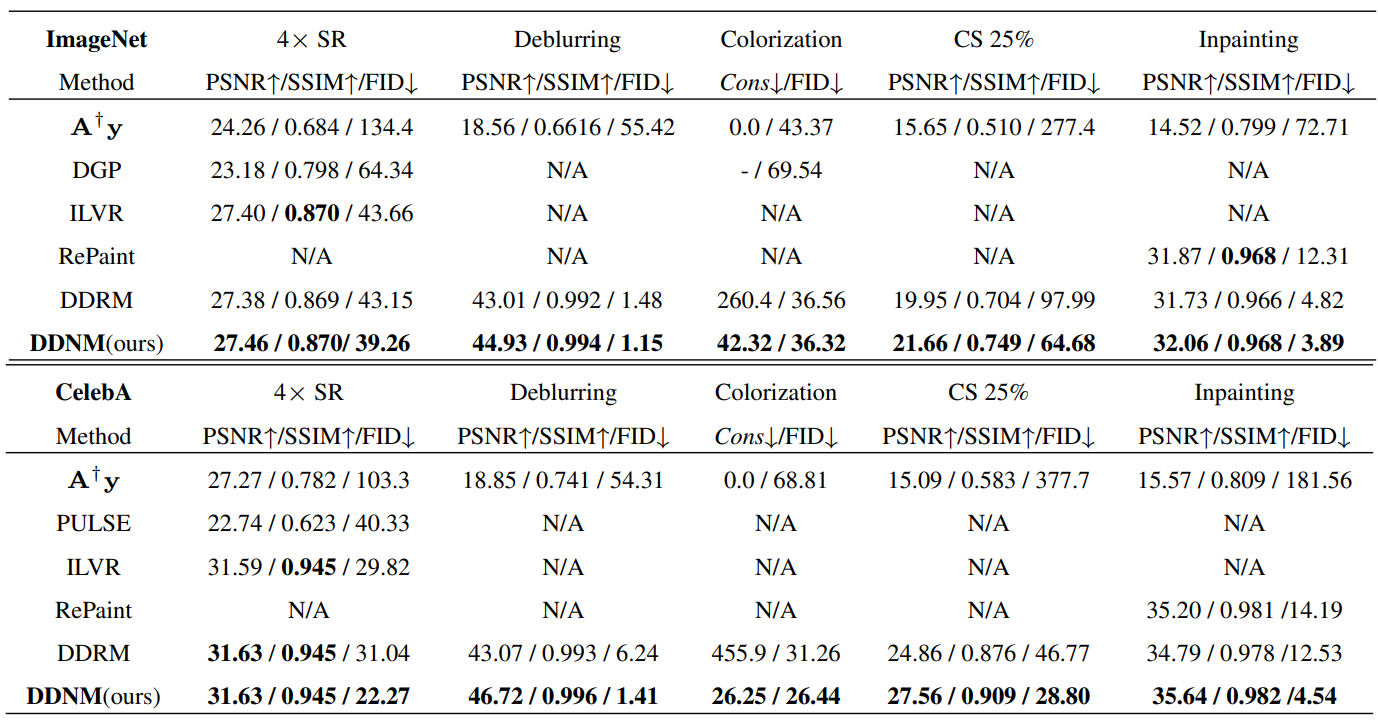
2. Evaluation on DDNM+

다음은 DDNM과 DDNM+의 성능을 비교한 표이다.

다음은 DDNM과 DDNM+의 denoising 성능(a)과 복구 품질(b)을 비교한 것이다.

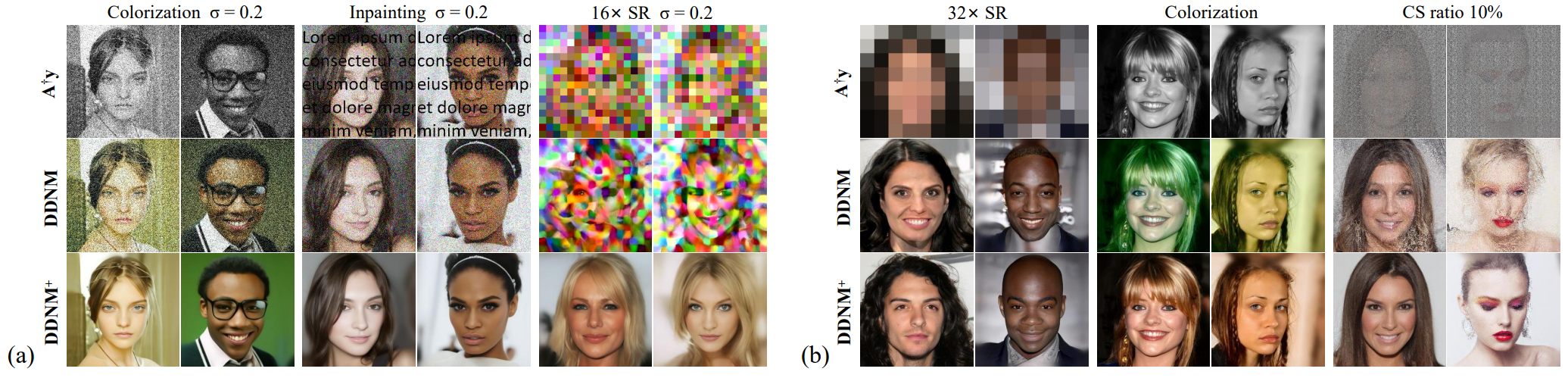
다음은 DDNM+을 zero-shot IR 방법과 정성적으로 비교한 샘플들이다.

3. Real-World Applications

다음은 DDNM+으로 강한 noise ($\sigma_y = 0.9$)를 포함한 4배 SR을 다루는 예시다.

다음은 JPEG와 같은 아티팩트를 DDNM+를 해결한 예시다.

다음은 오래된 사진을 복구한 예시다.

Mask-Shift Trick

저자들은 DDNM이 임의의 출력 크기를 갖는 IR task를 풀수 있도록 하기 위해 Mask-Shift trick을 제안한다.

Diffusion model은 일반적으로 출력 이미지 크기에 강력한 제약이 있다. 기본 DDNM의 결과 크기가 256$\times$256이라고 가정하자. 낮은 해상도의 이미지 $y$의 크기가 64$\times$256이고 이를 256$\times$1024로 super-resolution하고 싶다고 하자. 가장 간단한 방법은 $y$를 64$\times$64 크기의 이미지 4개로 나누고 DDNM으로 4개의 결과를 얻어 concat하는 것이다. 하지만, 이 방법은 각 분할 사이에 상당한 아티팩트를 가져온다.

여기서 저자들은 간단하지만 효과적인 트릭으로 이 문제를 완벽하게 해결한다. 위의 예시에서 먼저 $y$를 각 부분이 64$\times$32가 되도록 8개의 부분 $[y^{(0)}, \cdots, y^{(7)}]$로 나눈다. 먼저 $[y^{(0)}, y^{(1)}]$을 DDNM에 입력으로 넣어 SR 결과 $x$를 얻고 이를 $[x^{(0)}, x^{(1)}]$로 나눈다. 그런 다음 DDNM을 6번 사용하는 데, 각 $i$번째 때 $[y^{(i)}, y^{(i+1)}]$를 입력으로 사용하고 중간 결과

\[\begin{equation} \hat{x}_{0 \vert t} = [\hat{x}_{0 \vert t}^{(left)}, \hat{x}_{0 \vert t}^{(right)}] \end{equation}\]

의 왼쪽을

\[\begin{equation} \hat{x}_{0 \vert t} = [x^{(i)}, \hat{x}_{0 \vert t}^{(right)}] \end{equation}\]

로 대체한다. 최종 결과는 $[x^{(0)}, \cdots, x^{(7)}]$이 된다. 이 방법은 shift 사이의 재구성이 항상 일관되도록 보장한다. 이를 Mask-Shift trick이라 부른다. 임의의 크기의 입력 이미지 $y$에 대하여 먼저 zero-pad를 하고 수평 수직으로 나눈 다음 비슷한 Mask-Shift trick을 사용하면 수평과 수직의 일관성을 보장할 수 있다.

다음은 Mask-Shift trick을 사용하여 생성한 그림이다. 입력 이미지의 크기는 64$\times$256이고 출력 이미지의 크기는 256$\times$1024이다.