[논문리뷰] Diffusion-Based Voice Conversion with Fast Maximum Likelihood Sampling Scheme
ICLR 2022. [Paper] [Page]
Vadim Popov, Ivan Vovk, Vladimir Gogoryan, Tasnima Sadekova, Mikhail Kudinov, Jiansheng Wei
Huawei Noah’s Ark Lab, Moscow, Russia
28 Sep 2021
Introduction
Voice conversion (VC)는 source speaker가 발음한 발화의 언어적 내용을 보존하면서 target speaker의 음성을 복사하는 task이다. 실용적으로 VC를 적용하려면 임의의 source speaker와 target speaker에 대하여 one-shot 모드로 작동해야 한다. 이를 주로 one-shot many-to-many model (혹은 zero-shot many-to-many model이나 any-to-any VC model)이라고 부른다. 이러한 모델을 만드는 것이 어려운 이유는 모델이 처음 보는 목소리로 한 번만 발음된 발화에 적응해야 하기 때문이다. 따라서 최근까지 성공적인 one-shot VC 모델이 나타나지 않았다.
기존의 one-shot VC 모델은 autoencoder로 디자인된다. 인코더는 언어적 내용만을 이상적으로 포함하는 latent space를 가지며, target 음성의 identity 정보를 디코더에 조건으로 준다.
초기 AutoVC model은 사전 학습된 speaker verification network가 출력한 speaker embedding만을 조건으로 사용하였다. AutoVC를 개선시킨 여러 모델들은 pitch나 loudness 같은 phonetic feature들로 컨디셔닝을 풍부하게 만들거나 VC 모델과 speaker embedding network를 결합하여 학습시켰다. 또한 몇몇 논문에서는 attention mechanism으로 레퍼런스 발화의 특정 feature들을 source 발화에 더 좋게 합성하여 디코더의 성능을 개선하였다.
디코더에 풍부한 정보를 충분히 제공하는 것과는 별개로 autoencoder VC model의 주요 문제 중 하나는 인코더의 음성 컨텐츠에서 source speaker identity를 분리하는 것이다. 몇몇 모델은 이 문제를 해결하기 위해 information bottleneck을 제안하였다. 다른 해결책으로는 컨텐츠 정보에 벡터 양자화 테크닉을 적용하는 방법, VAE의 특징을 활용하는 방법, instance normalization layer를 사용하는 방법, PGG (Phonetic Posterirogram)을 사용하는 것이다.
본 논문에서 제안하는 모델은 이 분리 문제를 해결하기 위하여 인코더가 “average voice”를 예측하도록 하였다. 각 음소에 해당하는 mel feature들을 대규모 multi-speaker 데이터셋에서 평균화된 이 음소에 해당하는 mel feature로 변환하도록 학습시킨다.
디코더의 경우 음성 관련 task에서 좋은 결과를 보이는 Diffusion Probabilistic Model (DPM)로 디자인하였다. 한편 DPM은 고품질의 결과를 얻기 위해서는 수백 번의 iteraion이 필요하므로 느린 inference에 대한 문제가 있다.
이 문제를 해결하기 위해 저자들은 재학습 없이 괜찮은 품질의 샘플을 생성하면서 iteration의 수를 크게 줄이는 새로운 inference 방식을 개발하였다. 최근 DPM inference step의 수를 줄이려는 다양한 시도들이 있지만, 대부분은 특정 종류의 DPM에만 적용할 수 있다. 반면 본 논문의 방식의 모든 유명한 DPM에서 일반화할 수 있으며 likelihood maximization과 강한 상관관계가 있다.
Voice Conversion Diffusion Model
많은 VC 모델들과 같이 본 논문의 모델도 autoencoder의 구조를 가진다. 사실 데이터에 의존하는 prior가 있는 모든 조건부 DPM의 경우 forward diffusion은 인코더로 볼 수 있고 reverse diffusion은 디코더로 볼 수 있다. DPM은 forward process와 reverse process의 궤적 사이의 거리를 최소화하도록 학습되며, 이는 autoencoder 관점에서 보면 reconstruction error를 최소화하는 것이다.
본 논문의 접근 방식은 아래와 같이 요약할 수 있다.
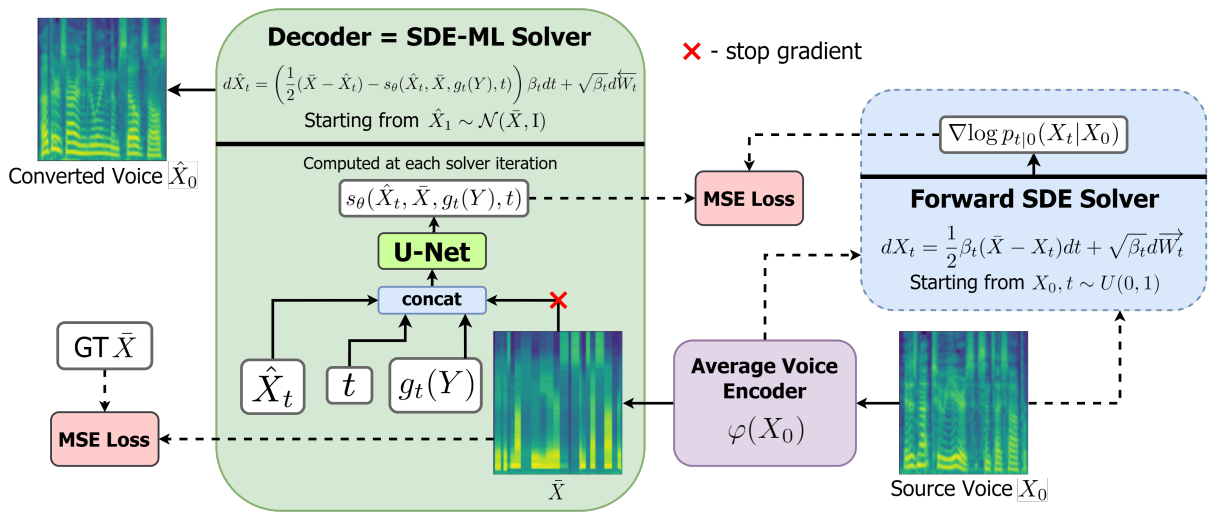
1. Encoder
저자들은 평균 음소 level의 mel feature를 speaker에 독립적인 음성 표현으로 선택하였다. 입력한 mel-spectrogram을 이 “average voice”로 변환하도록 인코더를 학습시키기 위하여 3가지 단계를 두었다.
- Montreal Forced Aligner을 대규모 multi-speaker LibriTTS 데이터셋에 적용하여 음소로 음성 프레임들을 align하였다.
- 전체 LibriTTS 데이터셋에 대하여 mel feature들을 집계하여 각 음소의 평균 mel feature를 얻는다.
- 인코더는 출력된 mel-spectrogram과 ground truth “average voice” 사이의 평균 제곱 오차를 최소화하도록 학습시킨다. 이를 통해 각 음소의 mel feature가 이전 단계에서 계산한 평균값으로 대체된다.
인코더는 Grad-TTS에서 사용한 Transformer 기반의 아키텍처와 동일하며, 입력으로 문자나 음소 임베딩 대신 mel feature가 들어가는 것만 다르다. Grad-TTS와 다르게 디코더와 분리하여 인코더를 학습시킨다.
2. Decoder
인코더가 forward diffusion의 마지막 분포를 parameterize하는 것과 달리 reverse diffusion은 디코더로 parameterize된다. Score-Based Generative Modeling through SDEs와 같은 방법으로 이산 시간 Markov chain 대신 stochastic process로 diffusion을 정의한다.
일반적인 DPM 프레임워크는 다음과 같은 SDE를 따르는 forward diffusion과 reverse diffusion으로 구성된다.
\[\begin{equation} dX_t = \frac{1}{2} \beta_t (\bar{X} - X) dt + \sqrt{\beta_t} d \overrightarrow{W}_t \\ d \hat{X}_t = \bigg( \frac{1}{2} (\bar{X} - \hat{X}_t) - s_\theta (\hat{X}_t, \bar{X}, t) \bigg) \beta_t dt + \sqrt{\beta_t} d \overleftarrow{W}_t \end{equation}\]$t \in [0,1]$이고, $\overrightarrow{W}$와 $\overleftarrow{W}$는 독립적인 Wiener process이다. $\beta_t$는 noise schedule이라 불리는 음이 아닌 함수이고 $s_\theta$는 score function이다.
Grad-TTS 논문에서 보인 것처럼 forward SDE는 다음과 같은 명시적 해를 갖는다.
\[\begin{equation} \textrm{Law} (X_t \vert X_0) = \mathcal{N} \bigg( e^{- \frac{1}{2} \int_0^t \beta_s ds} X_0 + \bigg( 1 - e^{- \frac{1}{2} \int_0^t \beta_s ds} \bigg) \bar{X}, \bigg( 1- e^{- \frac{1}{2} \int_0^t \beta_s ds} \bigg) I \bigg) \end{equation}\]따라서 만일 $e^{- \int_0^1 \beta_s ds} \approx 0$인 $\beta_0$과 $\beta_1$에 대하여 linear schedule가 $\beta_t = \beta_0 + t(\beta_1 - \beta_0)$를 만족한다면 $\textrm{Law} (X_1)$은 DPM의 prior인 $\mathcal{N} (\bar{X}, I)$에 가깝다.
Reverse diffusion은 다음과 같은 weighted $L_2$ loss를 최소화하여 학습된다.
\[\begin{equation} \theta^\ast = \underset{\theta}{\arg \min} \mathcal{L} (\theta) = \underset{\theta}{\arg \min} \int_0^1 \lambda_t \mathbb{E}_{X_0, X_t} \| s_\theta (X_t, \bar{X}, t) - \nabla \log p_{t \vert 0} (X_t \vert X_0) \|_2^2 dt \end{equation}\]여기서 $p_{t \vert 0} (X_t \vert X_0)$는 $\textrm{Law} (X_t \vert X_0)$의 확률 밀도 함수이며, $\lambda_t = 1- e^{- \int_0^t \beta_s ds}$이다. $\textrm{Law} (X_t \vert X_0)$가 가우시안이므로
\[\begin{equation} \nabla \log p_{t \vert 0} (X_t \vert X_0) = - \frac{X_t - X_0 e^{- \frac{1}{2} \int_0^t \beta_s ds} - \bar{X} (1- e^{- \frac{1}{2} \int_0^t \beta_s ds})}{1- e^{- \int_0^t \beta_s ds}} \end{equation}\]이다.
학습 시 $t$는 $[0,1]$에서 uniform하게 샘플링되며 $X_t$는 $\textrm{Law} (X_t \vert X_0)$로 생성된다. 위 식은 샘플들에 대한 손실 함수 $L$을 계산하는 데에 사용된다.
$\bar{X}$는 “average voice”이며 인코더 $\varphi$를 사용하여 $\bar{X} = \varphi(X_0)$로 변환할 수 있다. 디코더는 $s_\theta = s_\theta ( \hat{X}_t, \bar{X}, g_t (Y) , t)$로 컨디셔닝할 수 있으며, $g_t (Y)$는 학습 가능한 함수로 target speaker에 대한 정보를 제공한다. 이 함수는 디코더와 결합하여 학습되는 신경망이다. 저자들은 3가지 입력으로 실험을 진행하였다.
- d-only: 사전 학습된 speaker verification network에서 target mel-spectrogram $Y_0$로 추출한 speaker embedding
- wodyn: 추가로 noisy한 target mel-spectrogram $Y_t$를 입력을 사용
- whole: 추가로 forward diffusion \(\{ Y_s \vert s = 0.515, 1.5/15, \cdots, 14.5/15 \}\)의 모든 target mel-spectrogram 사용
디코더 아키텍터는 U-Net을 기반으로 하며 Grad-TTS와 동일하지만 4배 더 많은 채널로 사람 목소리의 전체 범위를 더 잘 포착하도록 하였다. Speaker conditioning network $g_t (Y)$는 2D conv layer들과 MLP들로 이루어져 있으며, 출력되는 128차원 벡터는 $\hat{X}_t$와 $\bar{X}$에 추가 128채널로 concat된다.
Maximum Likelihood SDE Solver
저자들은 forward diffusion의 샘플 경로들의 log-likelihood를 최대화하는 fixed-step first-order reverse SDE solver를 개발하였다. 이 solver는 다른 범용 Euler-Maruyama SDE solver와 매우 작은 값이 다르지만 몇 번의 iteration으로 diffusion model에서 샘플링할 때 중요해진다.
유클리드 공간에서 정의된 다음과 같은 forward SDE와 reverse SDE를 생각해보자.
\[\begin{equation} dX_t = - \frac{1}{2} \beta_t X_t dt + \sqrt{\beta_t} d \overrightarrow{W}_t d \hat{X}_t = \bigg( - \frac{1}{2} \beta_t \hat{X}_t - \beta_t s_\theta (\hat{X}_t, t) \bigg) dt + \sqrt{\beta_t} d \overleftarrow{W}_t \end{equation}\]$\overrightarrow{W}$는 forward Wiener process이고 $\overleftarrow{W}$는 backward Wiener process이다.
Score-Based Generative Modeling through SDEs 논문의 DPM을 Variance Preserving (VP)라 부른다. 저자들은 단순성을 위해 diffusion model의 특정 종류를 위한 maximum likelihood solver를 유도한다. VC diffusion model의 forward diffusion 식은 constant shift로 위의 forward 식으로 변환할 수 있으며, 이를 Mean Reverting Variance Preserving (MR-VP)라 부른다. VP 모델 분석은 쉽게 MR-VP 모델로 확장할 수 있으며 sub-VP와 VE 같은 다른 일반적인 diffusion model 종류도 확장 가능하다.
Forward SDE는 모든 $0 \le s < t \le 1$에 대하여 다음과 같이 명시적 해를 갖는다.
\[\begin{equation} \textrm{Law} (X_t \vert X_s) = \mathcal{N} (\gamma_{s,t} X_s, (1-\gamma_{s,t}^2) I), \quad \exp \bigg( - \frac{1}{2} \int_s^t \beta_u du \bigg) \end{equation}\]$s_\theta$로 parameterize한 reverse SDE는 $X_t$의 로그 밀도의 기울기를 근사하여 학습한다.
\[\begin{equation} \theta^\ast = \underset{\theta}{\arg \min} \int_0^1 \lambda_t \mathbb{E}_{X_t} \| s_\theta (X_t, t) - \nabla \log p_t (X_t) \|_2^2 dt \end{equation}\]$p_t (X_t)$는 $\textrm{Law} (X_t)$의 확률 밀도 함수이며 $\lambda_t$는 양의 가중치 함수이다. 강한 해의 존재성을 보장하기 위해서는 SDE의 계수가 특정 Lipschitz 제약을 만족해야 한다.
VP DPM의 생성 과정은 $\hat{X}_1 \sim \mathcal{N}(0, I)$에서 시작하여 시간을 거슬러 reverse SDE를 푸는 것으로 구성된다. 일반 Euler-Maruyama solver는 iteration의 수가 적으면 샘플 품질을 저해하는 이산화 오차가 존재한다. 또한 특정 SDE 종류에 대해서는 unbiased numerical solver나 exact numerical solver도 디자인할 수 있다.
Solver는 다음 값들의 항으로 표현되는 Theorem 1을 제안한다.
\[\begin{equation} \mu_{s,t} = \gamma_{s,t} \frac{1-\gamma_{0,s}^2}{1-\gamma_{0,t}^2}, \quad \nu_{s,t} = \gamma_{0,s} \frac{1-\gamma_{s,t}^2}{1-\gamma_{0,t}^2}, \quad \sigma_{s,t}^2 = \frac{(1-\gamma_{0,s}^2)(1-\gamma_{s,t}^2)}{1-\gamma_{0,t}^2} \\ \kappa_{t,h}^\ast = \frac{\nu_{t-h,t} (1-\gamma_{0,t}^2)}{\gamma_{0,t} \beta_t h} - 1, \quad \omega_{t,h}^\ast = \frac{\mu_{t, h,t} - 1}{\beta_t h} + \frac{1 + \kappa_{t,h}^\ast}{1 - \kappa_{0,t}^2} - \frac{1}{2}, \\ (\sigma_{t,h}^\ast)^2 = \sigma_{t-h, t}^2 + \frac{1}{n} \nu_{t-h, t}^2 \mathbb{E}_{X_t} [\textrm{Tr}(\textrm{Var}(X_0 \vert X_t))] \end{equation}\]Theorem 1. Reverse SDE로 특징지어지는 DPM이 최적으로 학습되었다고 가정하자. 임의의 자연수 $N \in \mathbb{N}$에 대하여 $h = 1/N$이라 두자. Step size가 $h$로 고정된 reverse SDE solver를 실수 triplet \(\{(\hat{\kappa}_{t,h}, \hat{\omega}_{t,h}, \hat{\sigma}_{t,h}) \vert t = h, 2h, \cdots, 1\}\)으로 다음과 같이 parameterize하는 것을 생각해보자.
\[\begin{equation} \hat{X}_{t-h} = \hat{X}_t + \beta_t h \bigg( \bigg( \frac{1}{2} + \hat{\omega}_{t,h} \bigg) \hat{X}_t + (1 + \hat{\kappa}_{t,h}) s_{\theta^\ast} (\hat{X}_t, t) \bigg) + \hat{\sigma}_{t,h} \xi_t \\ t = 1, 1-h, \cdots, h, \quad \quad \xi_t \sim N(0, I) \end{equation}\]그러면 다음이 성립한다.
-
생성 모델 $\hat{X}$에서 샘플 경로 \(X = \{X_{kh}\}_{k=0}^N\)의 log-likelihood는 \(\hat{\kappa}_{t,h} = \kappa_{t,h}^\ast\), \(\hat{\omega}_{t,h} = \omega_{t,h}^\ast\), \(\hat{\sigma}_{t,h} = \sigma_{t,h}^\ast\)에 대하여 최대화된다.
-
위의 SDE solver가 랜덤 변수 $\hat{X}_1 \sim \textrm{Law} (X_1)$에서 시작한다고 가정하자. 만일 $X_0$가 상수거나 isotropic한 대각 공분산 행렬 (ex. $\delta^2 I$ ($\delta > 0$))을 가지는 가우시안 랜덤 변수이면, 생성 모델 $\hat{X}$는 \(\hat{\kappa}_{t,h} = \kappa_{t,h}^\ast\), \(\hat{\omega}_{t,h} = \omega_{t,h}^\ast\), \(\hat{\sigma}_{t,h} = \sigma_{t,h}^\ast\)에 대하여 정확하다.
Theorem 1은 기존 방법과 비교했을 때 추가 계산 비용 없는 개선된 DPM 샘플링을 제안하며, 모델 재학습이나 광범위한 noise schedule 탐색이 필요 없다. Theorem 1은 이산적인 경로 \(X = \{X_{kh}\}_{k=0}^N\)에 대하여 reverse SDE solver의 최적성을 설정하였으며, 연속적인 경로 \(\{X_t\}_{t \in [0,1]}\)에서의 연속적인 모델의 최적성은 Score-Based Generative Modeling through SDEs 논문에서 보였듯이 $\theta = \theta^\ast$에서 보장된다.
Experiments
- 데이터셋: VCTK (109 speakers), LibriTTS (1100 speakers)
- VCTK는 처음과 끝의 조용한 부분을 제거하고 발화의 1.5초를 랜덤하게 선택해 디코더 학습에 사용
- Training hyperparameter
- 인코더: batch size 128, Adam optimizer (lr = 0.0005), VCTK는 500 epoch, LibriTTS는 300 epoch
- 디코더: batch size 32, Adam optimizer (lr = 0.0001), VCTK는 200 epoch, LibriTTS는 110 epoch
- Mel-spectrogram: 80 mel features, sampling rate 22.05kHz
- STFT: 1024 frequency bin, 1024 window size, hop size 256
- Diff-LibriTTS 모델은 mel 도메인에서 simple spectral subtraction algorithm (spectral floor parameter $\beta = 0.02$)을 사용하여 모델이 생성한 배경의 noise를 줄임.
- Mel-spectrogram inversion은 사전 학습된 HiFi-GAN으로 진행
샘플링은 다음과 같이 변형한 reverse SDE solver를 사용하였다.
\[\begin{equation} \hat{X}_{t-h} = \hat{X}_t + \beta_t h \bigg( \bigg( \frac{1}{2} + \hat{\omega}_{t,h} \bigg) (\hat{X}_t - \bar{X}) + (1 + \hat{\kappa}_{t,h}) s_{\theta^\ast} (\hat{X}_t, \bar{X}, g_t (Y) t) \bigg) + \hat{\sigma}_{t,h} \xi_t \\ t = 1, 1-h, \cdots, h, \quad \quad \xi_t \sim N(0, I) \end{equation}\]1. Speaker Conditioning Analysis

위 표는 Diff-VCTK와 Diff-LibriTTS 모두 wodyn이 최고의 옵션이라는 것을 보여준다.
2. Any-to-Any Voice Conversion
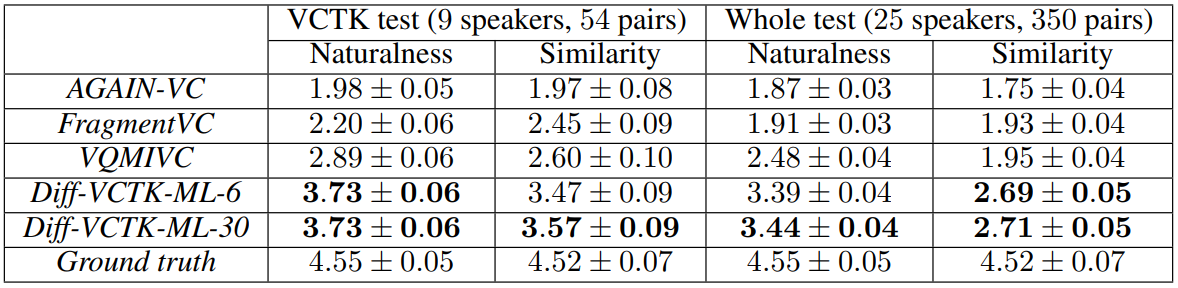
위 표는 본 논문의 모델이 자연스러움과 유사성에서 baseline 모델보다 상당히 우수함을 보여준다. ML은 maximum likelihood sampling을 의미하며, $ML-N$에서 $N = 1/h$은 SDE solver의 step 수이다.
다음은 여러가지 샘플링 방법으로 Diff-LibriTTS를 샘플링 한 것이다.
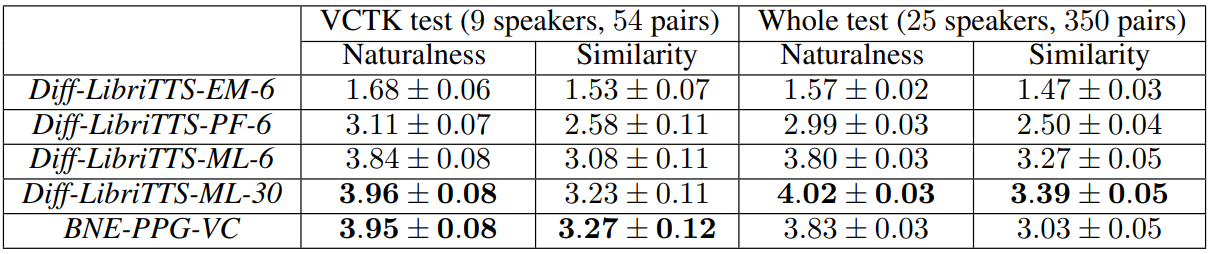
EM은 Euler-Maruyama solver로 실험한 것이고 PF는 probability flow sampling으로 실험한 것이다. Maximum likelihood sampling이 다른 샘플링 방법보다 더 우수한 성능을 보였다. 또한 작은 수의 inference step으로도 충분히 괜찮은 품질을 보였다.
3. Maximum Likelihood Sampling
다음은 다양한 reverse SDE solver를 FID로 비교한 것이다. $N$은 solver의 step 수이다.
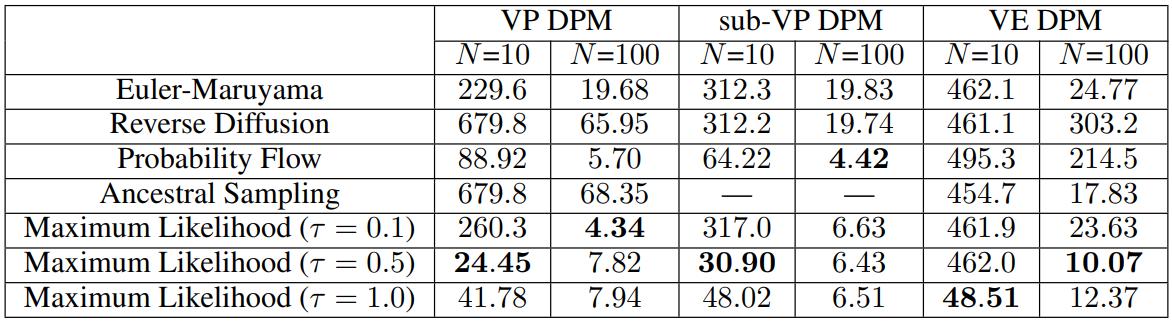
다음은 CIFAR-10 이미지를 VP DPM에서 10개의 step으로 랜덤하게 샘플링한 것이다. 왼쪽부터 euler-maruyama, probability flow, maximum likelihood ($\tau = 0.5$), maximum likelihood ($\tau = 1.0$)을 사용하였다.
