[논문리뷰] Scalable Autoregressive Monocular Depth Estimation

CVPR 2025. [Paper] [Page] [Github]
Jinhong Wang, Jian Liu, Dongqi Tang, Weiqiang Wang, Wentong Li, Danny Chen, Jintai Chen, Jian Wu
ZJU | Ant Group | University of Notre Dame | HKUST (Guangzhou)
18 Nov 2024

Introduction

최근 autoregressive (AR) 아키텍처는 다양한 task에서 강력한 일반화 능력과 상당한 scalability를 보여주었다. 이는 자연스럽게 흥미로운 질문으로 이어진다.

Monocular depth estimation (MDE)에 대한 autoregressive 모델을 개발할 수 있을까?

그러나 AR 모델링은 각 step의 예측이 이전 step과 논리적으로 연결되는 체계적인 순차적 데이터 구조에 의존한다. 이러한 순차적 의존성은 의미 있는 순차적 예측 타겟이 명확하지 않은 MDE와는 직관적으로 일치하지 않는다.

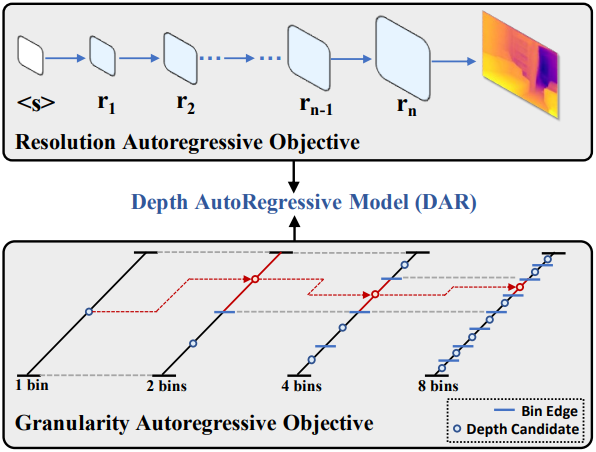
본 논문에서는 MDE를 위한 간단하고 효과적이며 scalable한 depth autoregressive (DAR) 프레임워크를 소개한다. 저자들은 MDE의 두 가지 주요 순서 속성을 활용하고 이를 autoregressive objective로 통합하였다.

1. Depth map 해상도: 낮은 해상도에서 높은 해상도로 정렬된 다양한 해상도의 depth map을 생성하고, 서로 다른 해상도의 depth map 시퀀스를 예측 타겟으로 처리한다. 이 접근 방식은 depth map 생성을 낮은 해상도에서 높은 해상도의 AR objective로 재구성하며, 각 step에서 이전 예측을 기반으로 더 높은 해상도의 depth map을 생성한다.
2. 본질적으로 연속적인 깊이 값: 기존 방법들은 깊이 값을 여러 간격(bin)으로 discretize하고 각 bin의 확률을 예측한다. 깊이 범위를 점점 더 미세한 간격으로 더욱 discretize함으로써 MDE를 coarse-to-fine AR objective로 재구성한다.

해상도 AR을 위해, 저자들은 patches-wise causal mask를 이용한 prefix 예측을 기반으로 다음 해상도 depth map을 예측하는 depth autoregressive transformer를 개발하였다. 세분성 AR을 달성하기 위해, 저자들은 Multiway Tree Bins (MTBin)이라는 새로운 binning 전략을 제안하였다. 이 전략은 이전 깊이 예측을 사용하여 해당 bin을 쿼리한 후, 각 bin을 후속 AR step에 대한 오차 허용 범위를 갖는 하위 bin으로 재귀적으로 세분화한다. 중요한 점은 이러한 bin이 최종 깊이 값을 계산할 뿐만 아니라 세분성 정보를 latent token map에 임베딩하여 depth map 생성 프로세스를 효과적으로 가이드한다는 것이다.

Method

1. Overview

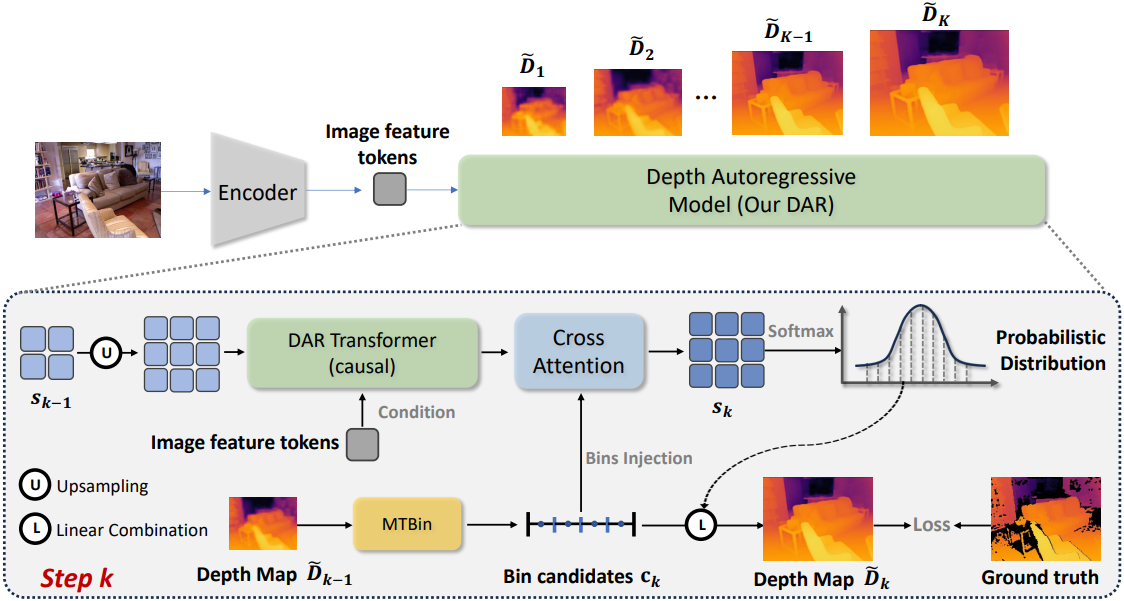
입력 RGB 이미지 $\mathcal{I} \in \mathbb{R}^{3 \times H \times W}$가 주어졌을 때, 이미지 $\mathcal{I}$의 depth map $\tilde{\mathcal{D}}$를 예측한다. 이 모델은 AR 과정에서 다양한 스케일의 depth map \(\{\tilde{\mathcal{D}}_1, \tilde{\mathcal{D}}_2, \ldots, \tilde{\mathcal{D}}_K\}\)을 점진적으로 예측한다. 즉, $k$ 단계에서 각 depth map은 이전 예측에 따라 다음과 같이 결정된다.

\[\begin{equation} p(\tilde{\mathcal{D}}_1, \tilde{\mathcal{D}}_2, \ldots, \tilde{\mathcal{D}}_K) = \prod_{k=1}^K p_\theta (\tilde{\mathcal{D}}_k \, \vert \, \tilde{\mathcal{D}}_1, \ldots, \tilde{\mathcal{D}}_{k-1}) \end{equation}\]

DAR은 데이터 집합에 대해 \(p_\theta (\tilde{\mathcal{D}}_k \, \vert \, \tilde{\mathcal{D}}_1, \ldots, \tilde{\mathcal{D}}_{k-1})\)을 최적화하고, 최종적으로 depth map \(\hat{\mathcal{D}} = \tilde{\mathcal{D}}_K\)를 예측한다.

DAR은 해상도와 세분성이라는 순서형 속성을 갖는 두 가지 AR objective를 포함한다. 해상도 AR objective는 저해상도에서 고해상도까지의 depth map을 예측하는 것을 목표로 하고, 세분성 AR objective는 coarse한 세분성에서 fine한 세분성까지의 depth map을 예측하는 것을 목표로 한다. 구체적으로 DAR은 네 부분으로 구성된다.

1. Image Encoder: RGB 이미지 feature를 latent 표현이 있는 이미지 토큰으로 추출한다.
2. DAR Transformer: Patch-wise causal mask를 통해 추출된 RGB 이미지 토큰을 조건으로 다양한 해상도의 토큰 맵을 점진적으로 예측한다.
3. Multiway Tree Bins (MTBin): 각 픽셀의 깊이 범위를 서로 다른 세분성의 bin으로 변환한다.
4. Bins Injection: Bin 후보의 정보를 활용하여 토큰 맵의 latent feature를 정제하는 것을 가이드한다.

2. Resolution Autoregressive Objective

DAR Transformer

DAR Transformer는 multi-headed self-attention (MSA) layer, layer normalization (LN), multi-headed cross-attention (MCA) layer으로 구성된 바닐라 Transformer 아키텍처를 따르며, 다양한 스케일의 logit 시퀀스를 예측하는 것을 목표로 한다. 깊이 추정은 주로 입력 RGB 이미지 feature를 기반으로 하기 때문에, 이미지 feature $X$를 조건으로 사용하여 깊이 추정을 제어한다.

각 step $k$에서, 먼저 이전 step의 토큰 맵 $r_{k−1}$을 다음 해상도로 업샘플링하여 입력 토큰 맵 $y_k$를 생성한다. DAR Transformer는 입력 쿼리로 $y_k$를 입력받아 MSA layer와 MCA layer로 전송하여 최종적으로 logit \(y_\textrm{out}^k\)를 생성한다. 여기서 MSA는 이전 토큰 맵 $y_{1:k}$를 입력받아 patch-wise causal mask를 통해 key와 value를 계산하고, MCA는 이미지 feature $X$를 입력받아 attention 계산을 수행한다. Step $k$에서 이 과정은 다음과 같다.

\[\begin{aligned} y_k &= \textrm{Upsampling} (r_{k-1}) \\ y_\textrm{hidden}^k &= \textrm{LN} (\textrm{MSA} (y_k W_Q; y_{1:k} W_K; y_{1:k} W_V; \textrm{Mask})) \\ y_\textrm{out}^k &= \textrm{LN} (\textrm{MCA} (y_\textrm{hidden}^k, X)) \end{aligned}\]

($W_Q$, $W_K$, $W_V$는 각각 query, key, value 계산을 위한 가중치 행렬, $\textrm{Mask}$는 patch-wise causal mask)

Logit \(y_\textrm{out}^k\)은 Bins Injection 모듈의 안내에 따라 step $k$의 latent token map $r_k$를 생성하는 데 사용된다. 이 과정에서 DAR은 이전 지식, 글로벌 이미지 feature, bin 후보 정보를 통합하여 고해상도 depth map 생성에 필요한 디테일한 feature를 충족할 수 있다.

Patch-wise Causal Attention Mask

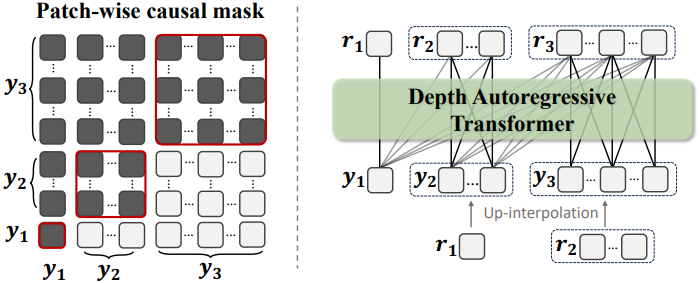
저자들은 다음 해상도 예측을 위해 전체 토큰 맵을 병합된 패치별 토큰으로 처리하는 patch-wise causal attention mask를 채택하였다. 이 마스크는 $y_k$의 각 토큰이 $y \le k$에 속하는 prefix 토큰과 $y_k$ 내의 다른 토큰과만 상호 작용할 수 있도록 보장한다.

3. Granularity Autoregressive Objective

Multiway Tree Bins (MTBin) Strategy

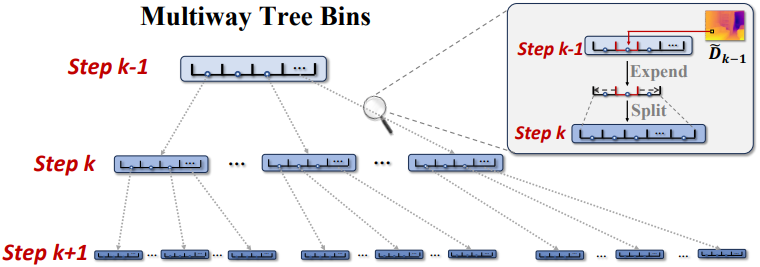
MTBin 전략은 이전 depth map의 예측을 사용하여 다음 step의 더 세밀한 깊이 예측을 위한 더 작은 bin을 생성하는 것을 목표로 한다. MTBin은 동일한 크기의 간격을 가진 고정된 개수의 bin을 사용하는 대신, 검색 범위를 점진적으로 줄여 더 높은 품질의 깊이를 재귀적으로 검색한다. 다음과 같이 step $k−1$에서 깊이 범위가 균일하게 $N$개의 bin으로 나뉜다고 가정하자.

\[\begin{equation} [\textbf{b}_{k-1}^1, \textbf{b}_{k-1}^2, \ldots, \textbf{b}_{k-1}^{N+1}] \end{equation}\]

(\(\textbf{b}_{k-1}^i\)는 $i$번째 bin의 왼쪽 경계, \(\textbf{b}_{k-1}^{N+1}\)은 $N$번째 bin의 오른쪽 경계)

픽셀 x에 대한 예측된 깊이 \(\tilde{\mathcal{D}}_{k-1} (\textbf{x})\)가 $t$번째 bin에 있다고 가정하자.

\[\begin{equation} \textbf{b}_{k-1}^t \le \tilde{\mathcal{D}}_{k-1} (\textbf{x}) \le \textbf{b}_{k-1}^{t+1} \end{equation}\]

그러면 MTBin은 이 bin을 더욱 세분화된 하위 bin으로 재귀적으로 분할하고 깊이 범위를 업데이트한다. 그러나 깊이 예측 오차로 인해 실제 값이 $t$번째 bin을 벗어날 수 있다. 따라서 모델의 오차 허용 범위를 유지하기 위해 새로운 깊이 범위를 먼저 인접한 bin으로 확장한 후, 이를 균일하게 하위 bin으로 분할한다.

\[\begin{aligned} L &= \frac{\textbf{b}_{k-1}^{\min \{ t+2, N+1 \}} - \textbf{b}_{k-1}^{\max \{ t-1, 1\}}}{N} \\ \textbf{b}_k^i = \textbf{b}_{k-1}^{t-1} + (i - 1) \cdot L, \quad i = 1, \ldots, N \end{aligned}\]

각 픽셀의 결정 과정은 고유하며, coarse한 단위에서 fine한 단위까지 점진적으로 세분화된다. 이러한 하위 bin은 Bins Injection을 통한 깊이 feature 모델링을 더욱 발전시키는 새로운 bin 후보 역할을 하며, 모델에서 예측한 토큰 맵의 softmax 값과 선형 결합을 수행하여 더욱 fine한 depth map을 얻는다. 구체적으로, step $k$에서 bin 중심을 깊이 후보로 사용할 수 있으며, 이는 다음과 같다.

\[\begin{equation} \textbf{c}_k^i = \frac{\textbf{b}_k^i + \textbf{b}_k^{i+1}}{2}, \quad i = 1, \ldots, N \end{equation}\]

픽셀당 softmax 값 $r_k$, 즉 깊이 후보와 연관된 확률 분포 \(\textbf{p}_k\)를 구하면, 선형 결합을 통해 최종 깊이를 계산한다.

\[\begin{equation} \tilde{\mathcal{D}}_k = \sum_{i=1}^N \textbf{c}_k^i \cdot \textbf{p}_k^i (\textbf{x}) \end{equation}\]

처음에는 전체 깊이 범위 \([d_\textrm{min}, d_\textrm{max}]\)를 균일하게 $N$개 bin으로 초기화한다.

\[\begin{equation} \textbf{b}_1^i = d_\textrm{min} + (i - 1) \cdot \frac{d_\textrm{max} - d_\textrm{min}}{N}, \quad i = 1, \ldots, N \end{equation}\]

Bins Injection

Bins Injection 모듈은 새로운 유효 깊이 범위와 bin 후보들을 활용하여 깊이 feature 모델링을 가이드하는 것을 목표로 한다. 먼저, 3$\times$3 convolutional layer를 통해 깊이 후보 \(\textbf{c}^k\)를 feature space에 projection한다. 그런 다음, 획득된 bin feature \(\textbf{f}_\textrm{bin}^k\)를 컨텍스트로 사용하여 ConvGRU 모듈을 통해 DAR Transformer의 출력 feature를 추가로 가이드한다.

\[\begin{aligned} \textbf{f}_\textrm{bin}^k &= \textrm{Conv}_{3 \times 3} (\textbf{c}^k) \\ r_k &= \textrm{ConvGRU} (y_\textrm{out}^k; \textbf{f}_\textrm{bin}^k) \end{aligned}\]

4. Other Details

Image Encoder

저자들은 기존 방식과의 공정한 비교를 위해, 이미지 인코더로 ViT를 선택했다 (Depth Anything과 동일). 조건부 이미지 feature 토큰은 이미지 인코더의 여러 레이어에서 feature map을 모두 입력 이미지의 1/8 해상도로 통합하여 얻어지며, 결과적으로 $1536 \times H/8 \times W/8$ 크기의 토큰 맵이 생성된다.

Loss Function

GT depth map에 누락된 값이 있으므로, GT depth map의 크기를 다른 해상도로 조정할 수 없다. 따라서 모든 예측된 depth map을 GT depth map과 동일한 크기로 업샘플링하고, 스케일링된 Scale-Invariant Loss를 계산하여 활용한다.

\[\begin{equation} \mathcal{L} = \sum_{k=1}^K \alpha \sqrt{\frac{1}{\vert \textbf{T} \vert} \sum_{\textbf{x} \in \textbf{T}} (\textbf{g}_k (\textbf{x}))^2 - \frac{\beta}{\vert \textbf{T} \vert^2} \left( \sum_{\textbf{x} \in \textbf{T}} \textbf{g}_k (\textbf{x}) \right)^2} \\ \textrm{where} \quad \textbf{g}_k (\textbf{x}) = \log \tilde{\mathcal{D}}_k (\textbf{x}) - \log \mathcal{D}_\textrm{gt} (\textbf{x}) \end{equation}\]

($K$는 최대 step 수, $\textbf{T}$는 유효한 GT 값을 갖는 픽셀 집합)

Experiments

• 구현 디테일
  • bin의 개수: $N = 16$
  • \([d_\textrm{min}, d_\textrm{max}]\): NYU Depth V2는 $[0.1, 10]$, KITTI는 $[0.1, 80]$
  • $K = 5$, $\alpha = 10$, $\beta = 0.85$
  • optimizer: AdamW
  • learning rate: $3 \times 10^{-5}$에서 $5 \times 10^{-4}$까지 선형 증가 후, 끝날 때까지 선형 감소
  • batch size: 16
  • epochs: 25
  • GPU: 학습에 NVIDIA A100 8개로 30분 소요

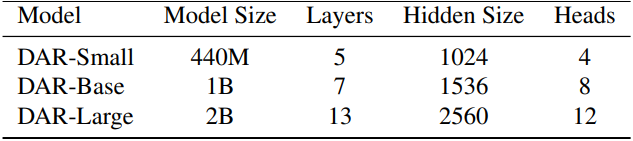
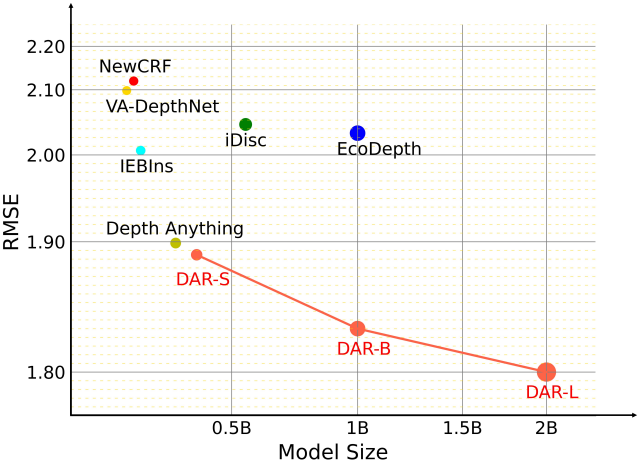
1. Comparisons with Previous Methods

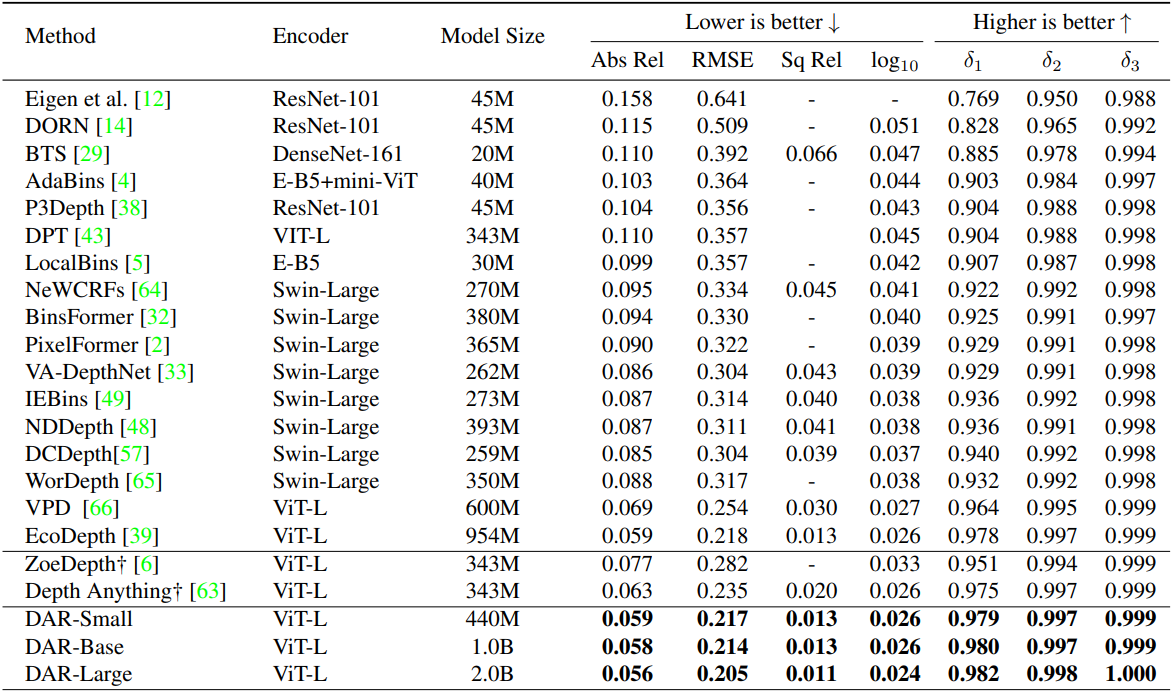
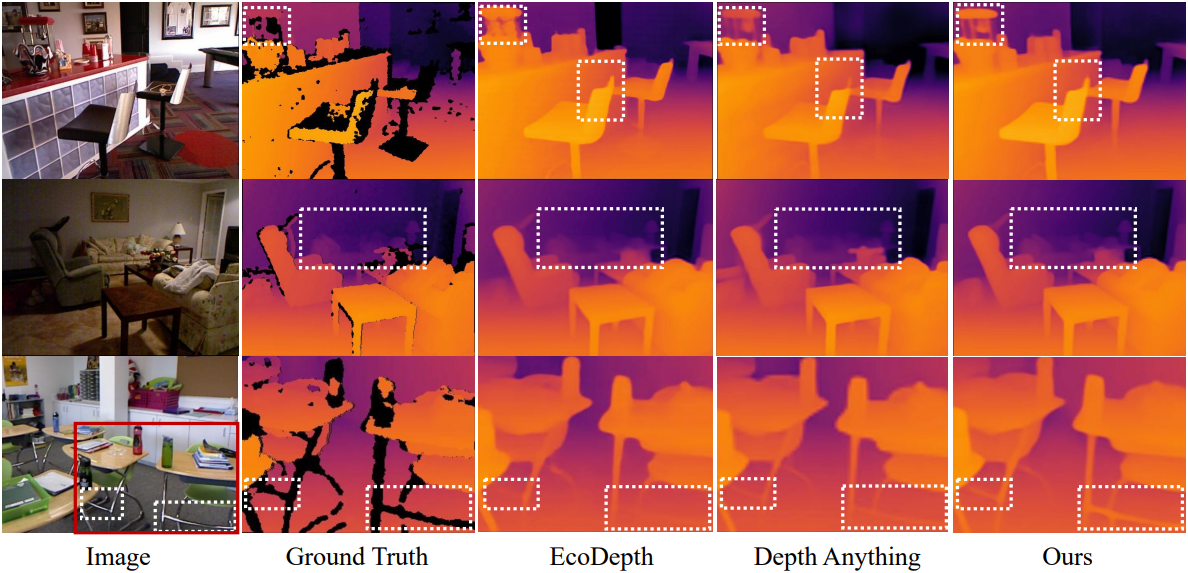
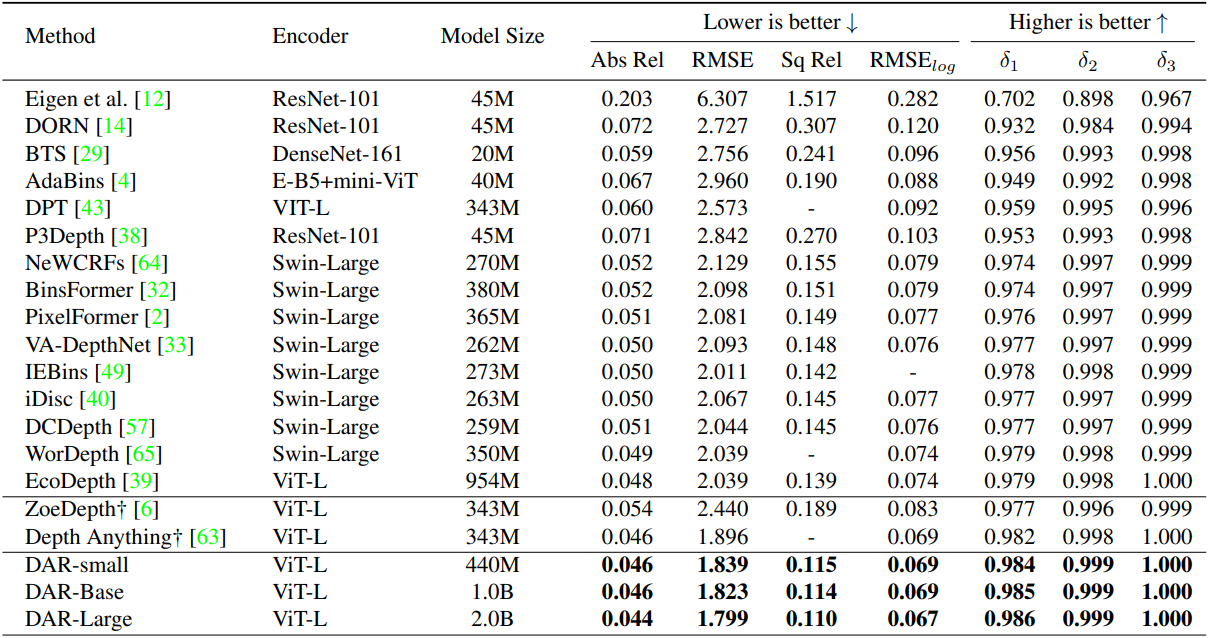
다음은 NYU Depth V2 데이터셋에서의 성능을 비교한 결과이다.

다음은 KITTI 데이터셋에서의 성능을 비교한 결과이다.

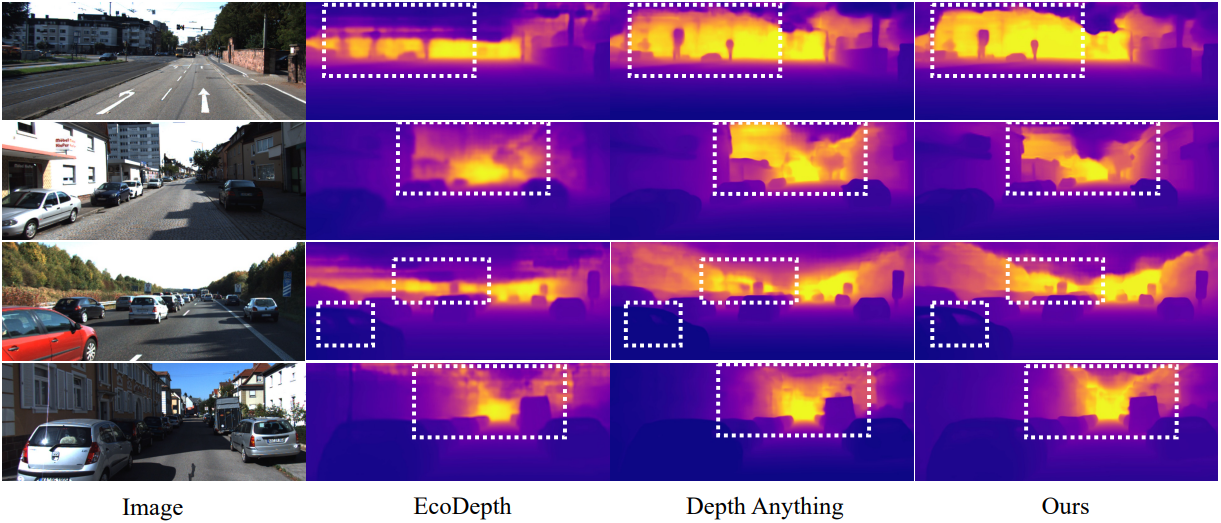
2. Zero-shot Generalization

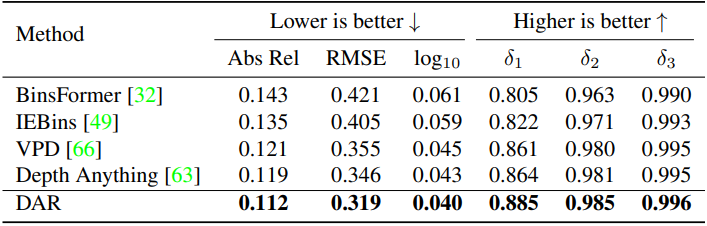
다음은 SUN RGB-D 데이터셋에서의 zero-shot 성능을 비교한 결과이다.

3. Ablation Study

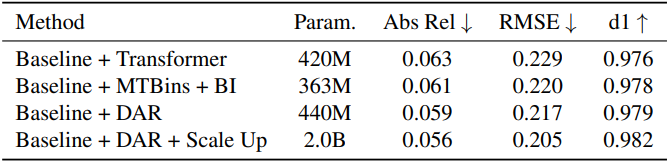
다음은 ablation study 결과이다. (BI: Bins Injection)

Limitations

1. Multi-step 패러다임은 더 매끄럽고 연속적이지만, 결과적으로 경계가 모호해지고 선명도가 떨어질 수 있다.
2. AR Transformer를 사용하기 때문에 DAR의 모델 파라미터 개수가 상대적으로 많으며, 특히 모델 크기를 scaling할 때 더욱 그렇다.