[논문리뷰] Diffusion Actor-Critic with Entropy Regulator
NeurIPS 2024. [Paper]
Yinuo Wang, Likun Wang, Yuxuan Jiang, Wenjun Zou, Tong Liu, Xujie Song, Wenxuan Wang, Liming Xiao, Jiang Wu, Jingliang Duan, Shengbo Eben Li
Tsinghua University | University of Science and Technology Beijing
24 May 2024
Introduction
본 논문에서는 online RL과 diffusion policy를 결합하는 새로운 일반화된 접근 방식인 DACER를 제안하였다. 구체적으로, DACER는 DDPM을 기반으로 한다. 본 논문에서는 diffusion model의 reverse process를 새로운 policy approximator로 재해석하고, 그 강력한 표현 능력을 활용하여 RL 알고리즘의 성능을 향상시켰다.
이 새로운 policy의 최적화 목표는 Q-value의 기대값을 최대화하는 것이다. RL에서 policy 탐색을 위해서는 엔트로피를 최대화하는 것이 중요하지만, diffusion policy의 엔트로피를 결정하는 것은 어렵다. 따라서, 고정된 간격으로 행동을 샘플링하고 Gaussian mixture model (GMM)을 사용하여 action 분포를 fitting한다. 이후, 각 state에서 policy의 엔트로피 근사값을 계산할 수 있다. 이러한 엔트로피들의 평균값을 현재 diffusion policy 엔트로피의 근사값으로 사용한다. 그런 다음, 추정된 엔트로피를 이용하여 diffusion policy의 exploration과 exploitation의 정도를 조절한다.
Method
1. Diffusion Policy Representation
본 논문은 조건부 diffusion model의 reverse process를 policy로 사용한다.
\[\begin{equation} \pi_\theta (\textbf{a} \vert \textbf{s}) = p_\theta (\textbf{a}_{0:T} \vert \textbf{s}) = p (\textbf{a}_T) \prod_{t=1}^T p_\theta (\textbf{a}_{t-1} \vert \textbf{a}_t, \textbf{s}) \\ \textrm{where} \quad p (\textbf{a}_T) = \mathcal{N}(0, \textbf{I}) \end{equation}\]Reverse process의 마지막 샘플 \(\textbf{a}_0\)를 RL 평가를 위한 action으로 사용한다. 저자들은 DDPM의 parameterization을 사용하여 \(p_\theta (\textbf{a}_{t-1} \vert \textbf{a}_t, \textbf{s})\)를 모델링하였다.
\[\begin{equation} p_\theta (\textbf{a}_{t-1} \vert \textbf{a}_t, \textbf{s}) = \mathcal{N} (\textbf{a}_{t-1}; \mu_\theta (\textbf{a}_t, \textbf{s}, t), \Sigma_\theta (\textbf{a}_t, s, t)) \\ \mu_\theta (\textbf{a}_t, \textbf{s}, t) = \frac{1}{\sqrt{\alpha}_t} \left( \textbf{a}_t - \frac{\beta_t}{\sqrt{1 - \bar{\alpha}_t}} \epsilon_\theta (\textbf{a}_t, s, t) \right), \quad \Sigma_\theta (\textbf{a}_t, s, t) = \beta_t I \\ \alpha_t = 1 - \beta_t, \quad \bar{\alpha}_t = \prod_{k=1}^t \alpha_k \end{equation}\]DDPM에서 action을 얻으려면 $T$개의 서로 다른 Gaussian 분포에서 순차적으로 샘플을 추출해야 한다. 샘플링 프로세스는 다음과 같이 재구성할 수 있다.
\[\begin{equation} \textbf{a}_{t-1} = \frac{1}{\sqrt{\alpha}_t} \left( \textbf{a}_t - \frac{\beta_t}{\sqrt{1 - \bar{\alpha}_t}} \epsilon_\theta (\textbf{a}_t, s, t) \right) + \sqrt{\beta_t} \epsilon, \quad \textrm{where} \; \epsilon \sim \mathcal{N}(0, \textbf{I}) \end{equation}\]2. Diffusion Policy Learning
Offline RL에 diffusion policy를 통합할 때, policy improvement는 behavior-cloning 항을 최소화하는 데 기반한다. 그러나 online RL에서는 모방할 데이터셋이 없으므로 behavior-cloning 항과 imitation learning 프레임워크를 배제한다. 본 논문에서 policy 학습의 목표는 주어진 state에 대하여 diffusion model이 생성하는 action들의 Q-value 기대값을 최대화하는 것이다.
\[\begin{equation} \max_\theta \mathbb{E}_{\textbf{s} \sim \mathcal{B}, \textbf{a}_0 \sim \pi_\theta (\cdot \vert \textbf{s})} [Q_\phi (\textbf{s}, \textbf{a}_0)] \end{equation}\]기존의 reverse process와는 달리, 본 논문에서는 전체 프로세스의 gradient를 기록해야 한다. Action에 대한 Q-value function의 gradient는 전체 diffusion 체인을 통해 backpropagation된다.
Q-value function은 double Q-learning trick을 사용하여 Bellman operator를 최소화하는 기존 접근 방식을 통해 학습된다. 두 개의 Q-network \(\textbf{Q}_{\phi_1}\), \(\textbf{Q}_{\phi_2}\)와 target network \(Q_{\phi_1^\prime}\), \(Q_{\phi_2^\prime}\)를 구축한다. 그러면, policy evaluation의 objective function은 다음과 같다.
\[\begin{equation} \min_{\phi_i} \mathbb{E}_{(\textbf{s}, \textbf{a}, \textbf{s}^\prime) \sim \mathcal{B}} \left[ \left( \left( r (\textbf{s}, \textbf{a}) + \gamma \min_{i=1,2} Q_{\phi_i^\prime} (\textbf{s}^\prime, \textbf{a}^\prime) \right) - Q_{\phi_i} (\textbf{s}, \textbf{a}) \right)^2 \right] \end{equation}\]\(\textbf{a}^\prime\)는 \(\textbf{s}^\prime\)을 diffusion policy에 입력하여 얻어지며, $\mathcal{B}$는 replay buffer이다. 저자들은 이를 바탕으로 DSAC에서 사용되는 기법을 활용하여 Q-value 과대평가 문제를 완화하였다.
본 논문에서 제시하는 diffusion policy는 policy 엔트로피를 필요로 하지 않는 주류 RL 알고리즘과 직접적으로 결합될 수 있다. 그러나 이 diffusion policy 학습 방법을 사용한 학습은 policy action이 지나치게 deterministic하게 이루어져 최종 diffusion policy의 성능이 저하되는 문제점을 안고 있다. 저자들은 이러한 문제를 해결하고 SOTA 성능을 달성하는 diffusion policy를 얻기 위해 엔트로피 추정 기법을 제안하였다.
3. Diffusion Policy with Entropy
Diffusion policy 분포의 엔트로피를 직접적으로 구할 수 없다. 그러나 동일한 state에서 여러 샘플을 사용하여 일련의 action들을 얻을 수 있다. 이러한 action 포인트들을 fitting함으로써 해당 state에 대응하는 action 분포를 추정할 수 있다.
본 논문에서는 policy 분포를 fitting하기 위해 Gaussian mixture model (GMM)을 사용하였다. GMM은 여러 개의 Gaussian 분포를 결합하여 복잡한 확률 밀도 함수를 형성하며, 이는 다음과 같이 표현될 수 있다.
\[\begin{equation} \hat{f} (\textbf{a}) = \sum_{k=1}^K w_k \cdot \mathcal{N}(\textbf{a} \vert \mu_k, \Sigma_k) \end{equation}\]($K$는 Gaussian 분포의 개수, $w_k$는 $k$번째 성분의 혼합 가중치)
각 state에 대해 diffusion policy를 사용하여 $N$개의 action \(\textbf{a}^1, \ldots, \textbf{a}^N\)을 샘플링한다. 그런 다음 Expectation-Maximization (EM) 알고리즘을 사용하여 GMM의 파라미터를 추정한다. Expectation 단계에서 각 데이터 포인트 \(\textbf{a}^i\)가 각 $k$번째 성분에 속할 사후 확률을 계산한다.
\[\begin{equation} \gamma (\textbf{z}_k^i) = \frac{w_k \cdot \mathcal{N}(\textbf{a}^i \vert \mu_k, \Sigma_k)}{\sum_{j=1}^K w_j \cdot \mathcal{N}(\textbf{a}^i \vert \mu_j, \Sigma_j)} \end{equation}\]Maximization 단계에서는 위 식의 계산 결과가 각 성분에 대한 파라미터 및 혼합 가중치를 업데이트하는 데 사용된다.
\[\begin{aligned} w_k &= \frac{1}{N} \sum_{i=1}^N \gamma (\textbf{z}_k^i) \\ \mu_k &= \frac{\sum_{i=1}^N \gamma (\textbf{z}_k^i) \cdot \textbf{a}^i}{\sum_{i=1}^N \gamma (\textbf{z}_k^i)} \\ \Sigma_k &= \frac{\sum_{i=1}^N \gamma (\textbf{z}_k^i) (\textbf{a}^i - \mu_k)(\textbf{a}^i - \mu_k)^\top}{\sum_{i=1}^N \gamma (\textbf{z}_k^i)} \end{aligned}\]파라미터가 수렴할 때까지 반복적인 최적화가 계속된다. 실험에서는 $K = 4$를 사용하였다.
State에 대응하는 action 분포의 엔트로피는 다음과 같이 추정할 수 있다.
\[\begin{equation} \mathcal{H}_\textbf{s} = - \sum_{k=1}^K w_k \log w_k + \sum_{k=1}^K w_k \cdot \frac{1}{2} \log ((2 \pi e)^d \vert \Sigma_k \vert) \end{equation}\]($d$는 action의 차원)
그런 다음, 선택된 state 배치와 관련된 action들의 엔트로피 평균을 diffusion policy의 추정 엔트로피 $\hat{\mathcal{H}}$로 사용한다.
Maximizing entropy RL과 유사하게, 추정된 엔트로피를 기반으로 파라미터 $\alpha$를 학습시킨다. 그리고 이 파라미터를 다음과 같이 업데이트한다.
\[\begin{equation} \alpha \leftarrow \alpha - \beta_\alpha [\hat{\mathcal{H}} - \bar{\mathcal{H}}] \end{equation}\](\(\bar{\mathcal{H}}\)는 target entropy)
마지막으로, 학습 중 diffusion policy 엔트로피를 조정하기 위해 diffusion policy의 출력에 noise를 더한다.
\[\begin{equation} \textbf{a} = \textbf{a} + \lambda \alpha \cdot \mathcal{N}(0, \textbf{I}) \end{equation}\]또한 평가 단계에서는 이 noise를 더하지 않는다.

Experiments
1. Comparative Evaluation
다음은 다양한 벤치마크에서의 training curve를 비교한 것이다.
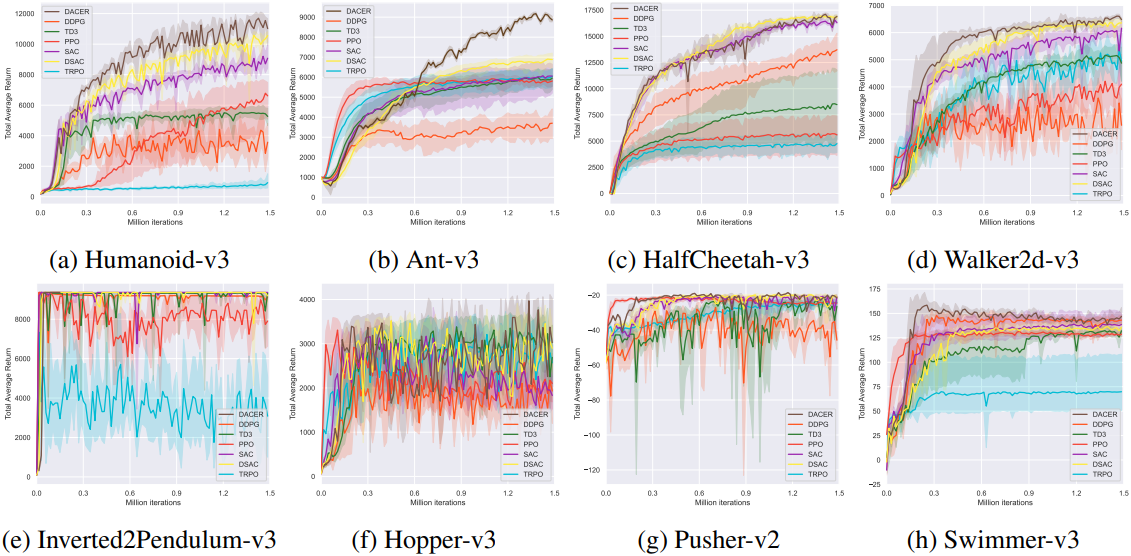
다음은 평균 return을 비교한

2. Policy Representation Experiment
다음은 diffusion policy의 표현 능력을 확인하기 위해 Multi-goal environment에서의 policy 분포와 value function을 비교한 결과이다.
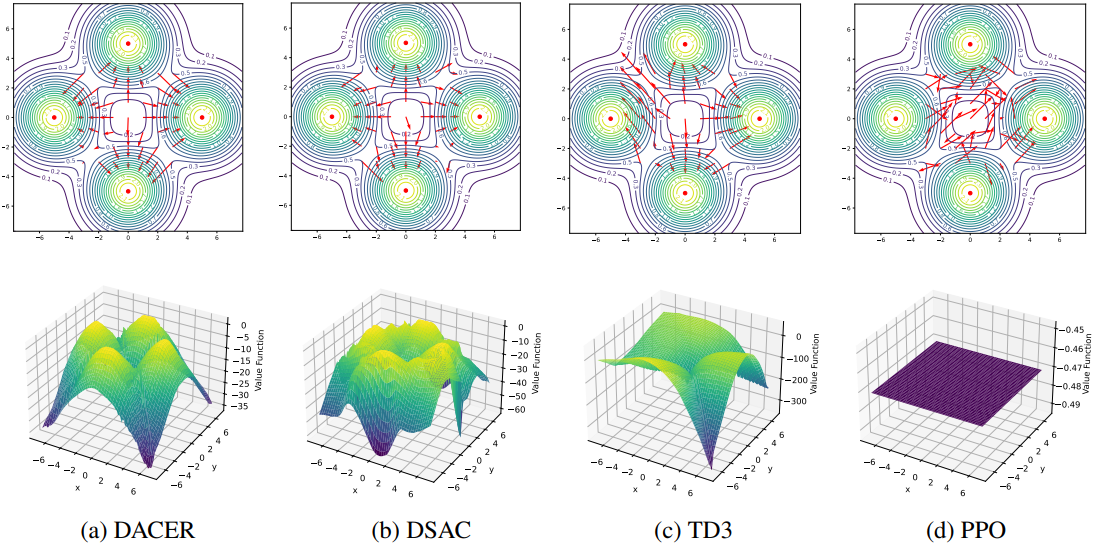
3. Ablation Study
다음은 엔트로피 사용 유무에 따른 training curve를 비교한 것이다.
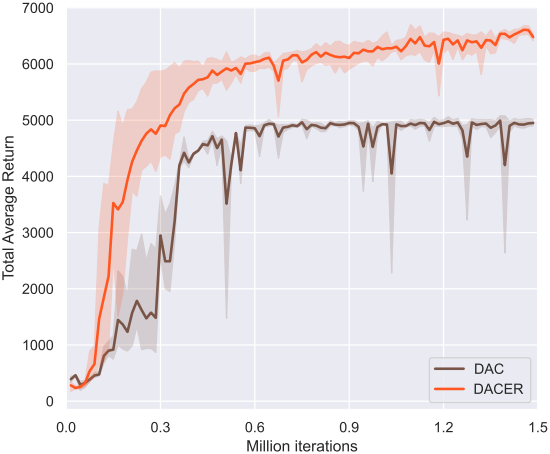
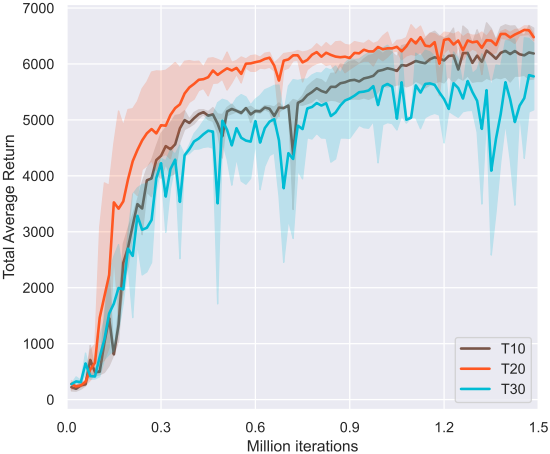
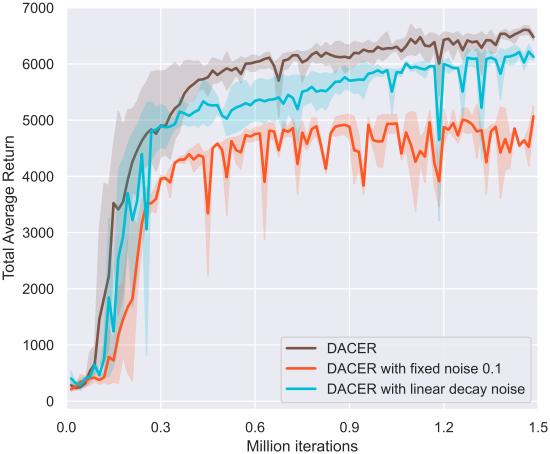
다음은 noise factor에 따른 training curve를 비교한 것이다.
다음은 diffusion timestep 수에 따른 training curve를 비교한 것이다.