[논문리뷰] D-Attn: Decomposed Attention for Large Vision-and-Language Models
ICCV 2025. [Paper] [Github]
Chia-Wen Kuo, Sijie Zhu, Fan Chen, Xiaohui Shen, Longyin Wen
ByteDance Intelligent Creation
4 Feb 2025
Introduction
최근 VLM은 사전 학습된 LLM의 기능을 활용하기 위해, 일반적으로 텍스트 토큰과 비주얼 토큰을 LLM의 입력으로 동등하게 concat하여 LLM 내의 텍스트 토큰 연산에 영향을 미치지 않도록 한다. 비전 인코더(ex. CLIP)에서 생성된 비주얼 토큰은 discrete tokenizer에서 얻은 텍스트 토큰과 본질적으로 다르다는 점을 고려할 때, 이러한 토큰을 하나의 S-Attn (Self-Attention)으로 처리하는 이러한 방식은 성능 및 효율성 측면에서 최적이 아닐 수 있다.
- LLM의 원래 위치 인코딩 방식에서 텍스트 토큰은 concat된 토큰 시퀀스에서 더 가까운 위치에 있는 비주얼 토큰에 본질적으로 더 많은 attention을 하는데, 이는 서로 다른 비주얼 토큰이 텍스트 토큰에 대해 동일하기 때문에 편향되고 바람직하지 않다.
- 비주얼 토큰이 $\vert V \vert$개 있을 때, 비주얼 토큰 간 S-Attn의 계산 복잡도는 $O(\vert V \vert^2)$이다. 비주얼 토큰이 양방향 transformer에서 생성되고 상관 정보가 인코딩되어 있기 때문에 중복성이 매우 높다.
X-Attn (Cross-Attention)을 탑재한 VLM은 비주얼 토큰 연산에 대한 설계에 더 큰 유연성을 제공한다. 예를 들어, 맞춤형 모듈이나 cross-attention block, Tanh 게이트와 같은 연산을 통해 비주얼 토큰을 LLM에 통합할 수 있다. 그러나 이러한 아키텍처는 사전 학습된 LLM의 무결성을 손상시키고 VLM의 성능 저하로 이어질 수 있다.
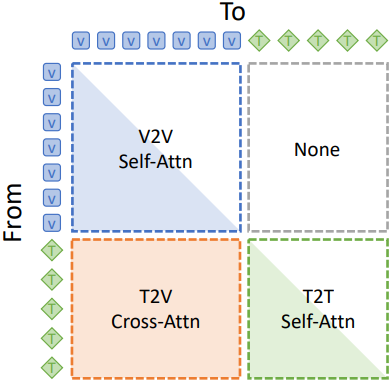
본 논문에서는 S-Attn과 X-Attn 사이의 간극을 메우는 새로운 attention 아키텍처인 Decomposed Attention (D-Attn)을 제안하였다. 즉, S-Attn의 성능 이점을 유지하면서 X-Attn의 설계 유연성을 확보하였다. Causal self-attention을 V2V SA, T2V XA, T2T SA로 분해함으로써, D-Attn은 LLM에 비전 정보를 더 잘 통합하기 위한 설계의 유연성을 확보하는 동시에, 비주얼 토큰과 텍스트 토큰 간의 병합 전략을 통해 LLM의 사전 학습된 성능을 최대한 보존한다.
저자들은 비주얼 토큰과 텍스트 토큰 간의 바람직하지 않은 위치 편향을 제거하기 위한 debiased positional encoding을 제안하였다. 이를 통해 LLM이 비전 정보를 더 잘 활용하여 시각적 이해 능력을 크게 향상시킬 수 있다. 또한 성능 저하 없이 비주얼 토큰에 대해 계산 복잡도를 $O(\vert V \vert^2)$에서 $O(\vert V \vert)$로 크게 줄이는 V2V diagonalization을 제안하였다.
Method
1. Debiased Positional Encodings
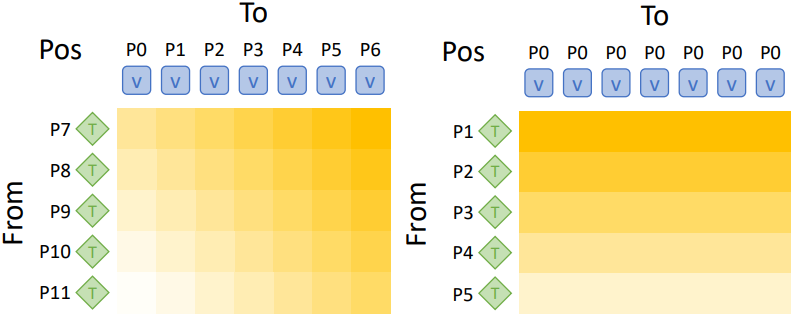
T2V XA에서 텍스트 토큰은 비주얼 토큰과 상호 작용하여 시각적 정보를 통합한다. 텍스트 토큰(query)은 비주얼 토큰(key, value)에 attention된다. 위 그림의 왼쪽에서 볼 수 있듯이, 위치 인코딩이 비주얼 토큰과 텍스트 토큰 사이의 위치 거리에 따라 attention 가중치를 왜곡하는 것을 볼 수 있다. 2D 비주얼 토큰은 일반적으로 행 우선 방식으로 평평하게 배치되므로, 이러한 attention 패턴은 텍스트 토큰이 이미지의 상단보다 하단에 더 많은 주의를 기울인다는 것을 의미한다. 이러한 편향은 시각적 콘텐츠에 대한 포괄적인 이해가 필요한 task에서 효과적인 비전-언어 상호 작용을 방해할 수 있다.
저자들은 비주얼 토큰의 위치를 동일한 값으로 설정하여 T2V XA의 편향을 제거하는 방안을 제안하였다. 예를 들어, 위 그림의 오른쪽에서 볼 수 있듯이 모든 비주얼 토큰의 위치를 P0로 설정한다. 이렇게 하면 각 텍스트 토큰이 모든 비주얼 토큰에 대해 균일한 attention 가중치 편향을 갖게 되어 시각적 콘텐츠에 대한 포괄적인 이해를 향상시키고 결과적으로 더 높은 성능을 얻을 수 있다.
2. V2V Diagonalization
V2V SA에서 각 비주얼 토큰은 다른 모든 비주얼 토큰에 인과적으로 접근하여 비주얼 토큰 간의 쌍별 상호작용을 모델링한다. $\vert V vert$개의 비주얼 토큰 시퀀스가 주어졌을 때, V2V SA의 계산 복잡도는 $O(\vert V \vert^2)$이며, 이는 고해상도 이미지나 수백 프레임의 동영상을 처리하는 데 문제가 될 수 있다.
V2V SA의 attention 가중치 행렬이 대각선에 집중되어 있어 각 비주얼 토큰이 주로 자기 자신과 attention된다는 관찰 결과에 착안하여, 저자들은 계산 복잡도를 크게 줄이기 위해 V2V SA를 대각화(diagonalization)하는 방안을 제안하였다. V2V diagonalization에서 각 비주얼 토큰은 다른 모든 비주얼 토큰이 아닌 자기 자신에게만 attention되므로 계산 복잡도는 $O(\vert V \vert)$로 감소할 수 있다.
\[\begin{aligned} \bar{V} &= \textrm{SA} (V, V) \\ &= \textrm{fc}_o \left( \underbrace{\textrm{softmax} \left( \frac{\textrm{fc}_q (V) \textrm{fc}_k (V)^\top}{\sqrt{d}} \right)}_{\textrm{diagonalize}} \textrm{fc}_v (V) \right) \\ &= \textrm{fc}_o (I_\textrm{\vert V \vert \times \vert V \vert} \textrm{fc}_v (V)) = \textrm{fc}_o (\textrm{fc}_v (V)) \end{aligned}\](\(\textrm{fc}_q\), \(\textrm{fc}_k\), \(\textrm{fc}_v\), \(\textrm{fc}_o\)는 각각 query, key, value, output에 대한 fully connected layer)
Softmax attention 행렬을 항등 행렬로 변환함으로써, 각 비주얼 토큰이 자기 자신에게만 attention되도록 강제하여 비주얼 토큰 간의 쌍별 상호작용을 피할 수 있다. 이러한 대각화는 self-attention 연산을 두 개의 fully connected layer로 단순화하여 계산 복잡도를 $O(\vert V \vert^2)$에서 $O(\vert V \vert)$로 크게 줄인다. 따라서 비주얼 토큰의 개수가 증가하는 고해상도 이미지나 긴 동영상 입력을 처리할 때 특히 유용하다.
3. Decomposed Attention

성능과 효율성을 향상시키기 위해 debiased positional encoding과 V2V diagonalization은 causal self-attention 메커니즘이 분해될 수 있다는 가정에 기반한다. 수학적으로 V2V SA, T2V XA, T2T SA의 세 블록으로 분해하는 방법과 블록들이 상호 작용하는 방식을 도출할 수 있다.
비주얼 토큰 $v$는 다른 비주얼 토큰 $V$에만 attention한다. 따라서 비주얼 토큰에 대한 attention 출력 $\bar{v}$는 다음과 같다.
\[\begin{equation} \bar{v} = \textrm{Attn}(v, V) = \textrm{SA}(v, V) \end{equation}\]반면, 텍스트 토큰 $t$는 비주얼 토큰 $V$와 텍스트 토큰 $T$ 모두에 attention하며, 이는 T2V XA와 T2T SA 간의 상호작용을 나타낸다. 수학적으로, 텍스트 토큰에 대한 attention 출력 $\bar{t}$는 다음과 같이 표현될 수 있다.
\[\begin{equation} \bar{t} = \textrm{Attn}(t, [V, T]) = \sum_i^L \frac{\exp (\textbf{q}_t \cdot \textbf{k}_i)}{\sum_l^L \exp (\textbf{q}_t \cdot \textbf{k}_l)} \textbf{v}_i \end{equation}\]($\textbf{q}$, $\textbf{k}$, $\textbf{v}$$는 각각 attention 모듈 내에서 projection된 query, key, value, $\textbf{k}$와 $\textbf{v}$는 $[V, T]$에서 projection됨)
$N$개의 비주얼 토큰과 $M$개의 텍스트 토큰에 대해, \(\textbf{k}_i\)와 \(\textbf{v}_i\)는 다음과 같다.
\[\begin{aligned} \textbf{k}_i &\in \{ \textbf{k}_{v_1}, \ldots, \textbf{k}_{v_N}, \textbf{k}_{t_1}, \ldots, \textbf{k}_{t_M} \} \\ \textbf{v}_i &\in \{ \textbf{v}_{v_1}, \ldots, \textbf{v}_{v_N}, \textbf{v}_{t_1}, \ldots, \textbf{v}_{t_M} \} \end{aligned}\]그러면 \(\bar{t}\)에 대한 식은 다음과 같이 다시 쓸 수 있다.
\[\begin{aligned} \bar{t} &= \sum_i^L \frac{\exp (\textbf{q}_t \cdot \textbf{k}_i)}{\sum_l^L \exp (\textbf{q}_t \cdot \textbf{k}_l)} \textbf{v}_i = \sum_i^N \frac{\exp (\textbf{q}_t \cdot \textbf{k}_{v_i})}{\sum_l^L \exp (\textbf{q}_t \cdot \textbf{k}_l)} \textbf{v}_{v_i} + \sum_i^M \frac{\exp (\textbf{q}_t \cdot \textbf{k}_{t_i})}{\sum_l^L \exp (\textbf{q}_t \cdot \textbf{k}_l)} \textbf{v}_{t_i} \\ &= \frac{\sum_n^N \exp (\textbf{q}_t \cdot \textbf{k}_{v_n})}{\sum_l^L \exp (\textbf{q}_t \cdot \textbf{k}_l)} \sum_i^N \frac{\exp (\textbf{q}_t \cdot \textbf{k}_{v_i})}{\sum_n^N \exp (\textbf{q}_t \cdot \textbf{k}_{v_n})} \textbf{v}_{v_i} + \frac{\sum_m^M \exp (\textbf{q}_t \cdot \textbf{k}_{t_m})}{\sum_l^L \exp (\textbf{q}_t \cdot \textbf{k}_l)} \sum_i^N \frac{\exp (\textbf{q}_t \cdot \textbf{k}_{t_i})}{\sum_m^M \exp (\textbf{q}_t \cdot \textbf{k}_{t_m})} \textbf{v}_{t_i} \\ &= \frac{\sum_n^N \exp (\textbf{q}_t \cdot \textbf{k}_{v_n})}{\sum_l^L \exp (\textbf{q}_t \cdot \textbf{k}_l)} \textrm{XA}(t, V) + \frac{\sum_m^M \exp (\textbf{q}_t \cdot \textbf{k}_{t_m})}{\sum_l^L \exp (\textbf{q}_t \cdot \textbf{k}_l)} \textrm{SA}(t, T) \\ &\equiv \alpha_V \textrm{XA}(t, V) + \alpha_T \textrm{SA}(t, T) \\ \end{aligned}\]수치적 안정성을 위해 다음과 같이 지수의 합에 로그를 취한다.
\[\begin{equation} S_V = \log \left( \sum_n^N \exp (\textbf{q}_t \cdot \textbf{k}_{v_n}) \right), \quad S_T = \log \left( \sum_m^M \exp (\textbf{q}_t \cdot \textbf{k}_{t_m}) \right) \end{equation}\]그러면 가중치 \(\alpha_V\)와 \(\alpha_T\) 다음과 같이 표현될 수 있다.
\[\begin{aligned} \alpha_V &= \frac{\sum_n^N \exp (\textbf{q}_t \cdot \textbf{k}_{v_n})}{\sum_l^L \exp (\textbf{q}_t \cdot \textbf{k}_l)} = \frac{\exp (S_V)}{\exp (S_V) + \exp (S_T)} = \frac{1}{1 + \exp (-(S_V - S_T))} \\ &= \textrm{Sigmoid}(S_V - S_T) \\ \alpha_T &= \textrm{Sigmoid}(S_T - S_V) = 1 - \alpha_V \\ \end{aligned}\]따라서, 입력 텍스트 토큰에 대한 attention 출력 $\bar{t}$는 T2V XA와 T2T SA의 가중 합으로 표현될 수 있다.
\[\begin{equation} \bar{t} = \textrm{Attn}(t, [V, T]) = \alpha_V \textrm{XA}(t, V) + \alpha_T \textrm{SA}(t, T) \end{equation}\]위에서 도출된 causal self-attention 분해를 통해, debiased positional encoding과 V2V diagonalization을 매끄럽게 통합할 수 있다. 구체적으로, T2V XA에 debiased positional encoding을 적용한 후, T2T SA와 결합한다. 또한, V2V SA에 V2V diagonalization을 적용할 수도 있다.
이러한 분해는 LLM 내에서 비주얼 토큰과 텍스트 토큰을 서로 다르게 처리할 수 있는 유연성을 제공한다. 또한, causal self-attention 메커니즘에 구조적 및 운영적 변경을 도입하지 않기 때문에 사전 학습된 LLM의 성능을 유지하면서 탁월한 시각적 이해 성능을 달성할 수 있다.
Experiments
1. Main Results
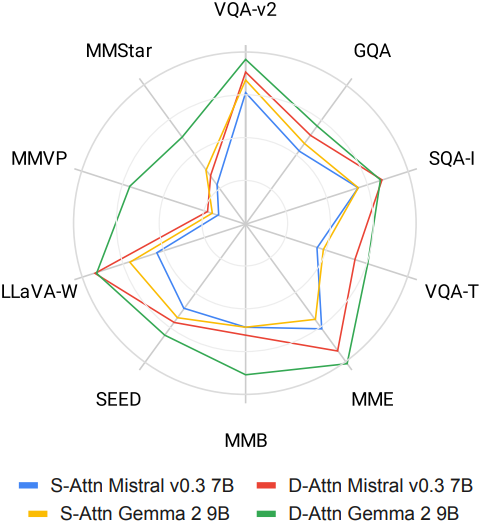
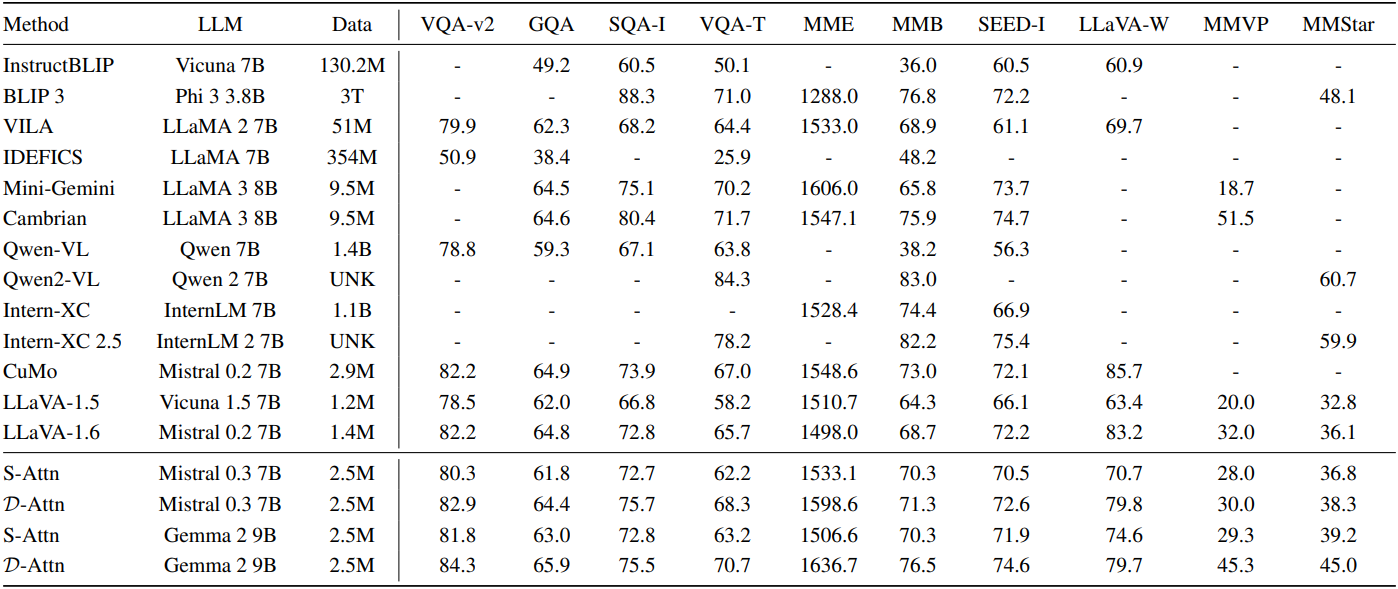
다음은 D-Attn 모델을 S-Attn 모델 및 다른 SOAT 모델과 비교한 결과이다.
다음은 D-Attn 모델의 출력을 S-Attn 모델과 비교한 예시들이다.

2. Ablations and Analysis
다음은 V2V diagonalization과 debiased positional encoding에 대한 ablation 결과이다.

다음은 토큰 병합 전략에 대한 ablation 결과이다.

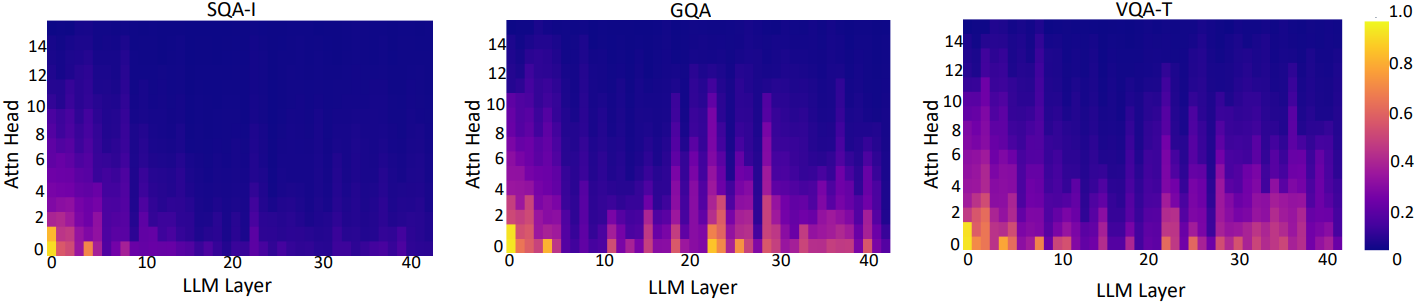
다음은 SQA-I, GQA, VQA-T 벤치마크에서 \(\alpha_V\) 값을 시각화한 결과이다.
다음은 위에서부터 MME, SEED, MMB 벤치마크에 대한 S-Attn과의 디테일한 비교 결과들이다.


