Diffusion은 신이고 GPT는 무적이다

ECCV 2024. [Paper] [Page]
Avinash Paliwal, Wei Ye, Jinhui Xiong, Dmytro Kotovenko, Rakesh Ranjan, Vikas Chandra, Nima Khademi Kalantari
Texas A&M University | Meta Reality Labs | LMU Munich
28 Mar 2024

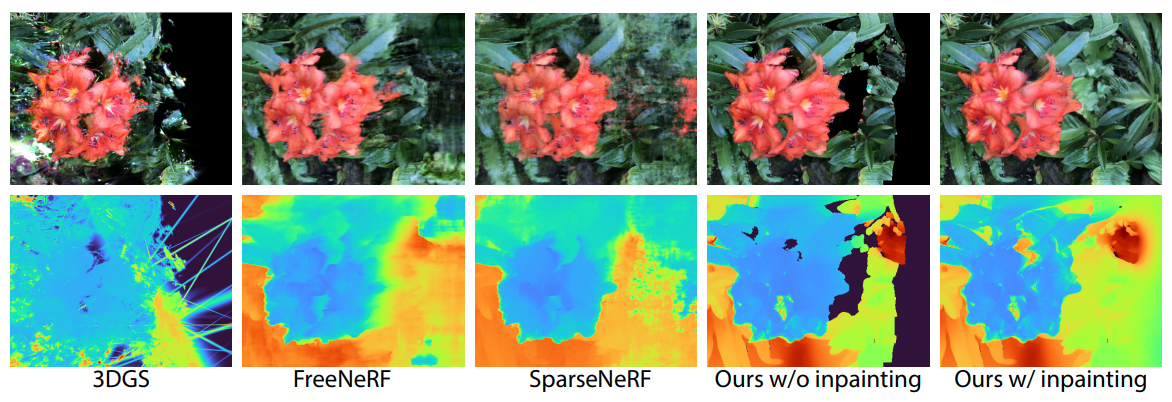
Introduction

3D Gaussian Splatting (3DGS)은 sparse한 학습 이미지 집합이 주어지면 좋은 표현을 생성하는 데 어려움을 겪는다. 이러한 경우 표현은 학습 뷰에 심하게 overfitting되고 새로운 뷰에서 거의 랜덤한 덩어리들의 모음으로 나타난다.

본 논문의 핵심 아이디어는 최적화 중에 Gaussian 덩어리의 움직임을 제한하여 Gaussian을 일관성 있게 만드는 것이다. Gaussian의 비정형적 특성으로 인해 3D 공간에서 이를 제한하는 것은 어렵다. 이 문제를 극복하기 위해 각 입력 이미지의 모든 픽셀에 하나의 Gaussian을 할당하고 2D 이미지 공간에서 단일 뷰 제약조건과 멀티 뷰 제약조건을 적용한다. 구체적으로, 신경망 디코더를 사용하여 유사한 깊이를 가진 각 이미지의 Gaussian이 일관되게 움직이도록 한다.

서로 다른 뷰에서의 Gaussian에 대한 제약 조건을 적용하기 위해, 모든 Gaussian을 사용하여 렌더링된 깊이가 total variance loss를 통해 매끄럽도록 보장한다. 또한 두 이미지에서 해당 픽셀의 Gaussian 위치가 유사하도록 보장하기 위해 flow 기반 loss를 사용한다.

최적화를 돕기 위해 기존 monocular depth 예측 모델을 사용하여 Gaussian의 위치를 ​​초기화한다. 이러한 모델은 고품질 깊이 추정치를 제공하지만 monocular depth는 상대적이며 뷰 전체에서 일관성이 없다. 깊이 기반 초기화는 Gaussian을 world-space에서 적절하게 배치하는 반면, 정규화된 최적화는 특히 위치에 대한 업데이트가 일관되고 매끄럽도록 장려한다. 추가로, Gaussian이 3D 공간에서 자유롭게 움직이는 것을 방지하기 때문에 가려진 영역을 쉽게 식별하고 인페인팅하여 고품질 텍스처와 형상으로 채울 수 있다.

Method


$N$개의 이미지 (ex. 3개 또는 4개)가 주어지면, 본 논문의 목표는 정적 장면의 3D Gaussian 표현을 재구성하는 것이다. 핵심 아이디어는 최적화 중에 3D Gaussian에 일관성(coherency)을 도입하는 것이다. 즉, Gaussian의 위치가 업데이트되면 최적화 중에 이웃 Gaussian도 비슷한 영향을 받아야 한다. 이러한 일관성을 통해 최적화를 더욱 제한하고 입력 이미지에 대한 overfitting을 방지할 수 있다.

1. Coherent 3D Gaussian Optimization


3D에서 자유롭게 움직이는 Gaussian 입자에 일관성을 도입하는 것은 어려운 일이다. 주요 아이디어는 2D 이미지 도메인에서 보다 구조화된 형태로 표현을 변환하는 것이다. 이를 위해 모든 입력 이미지의 각 픽셀에 하나의 Gaussian을 할당한다. 또한 각 픽셀에서 Gaussian의 움직임을 카메라 중심과 해당 픽셀을 연결하는 광선으로 제한한다. 이 표현에서 각 Gaussian의 위치는 스칼라 깊이 값을 사용하여 제어할 수 있다. 구체적으로, 각 픽셀에서 초기 깊이 추정치가 주어지면 다음과 같이 residual depth를 통해 각 Gaussian의 위치를 ​​업데이트한다.

\[\begin{equation} \mathbf{x} = g(D_n^\textrm{init} [\mathbf{p}] + \Delta D_n [\mathbf{p}], \mathbf{p}) \end{equation}\]

함수 $g(d, p)$는 픽셀 $p$를 깊이 $d$에 따라 3D로 projection한다. 각 뷰 \(D_n^\textrm{init}\)에서 로컬한 표면 형상이 초기 depth map에 의해 합리적으로 캡처된다고 가정하면, residual depth는 부정확성을 조정하기 위해서만 부드럽게 변해야 한다. 이 관찰을 바탕으로, 단일 뷰 및 멀티 뷰 제약 조건을 사용한다.

단일 뷰 제약조건

Convolutional 디코더를 활용하여 뷰별 부드러움(smoothness)을 강제한다. 구체적으로, 이 디코더는 뷰 인덱스 $n$을 입력으로 사용하고 전체 이미지의 residual depth를 추정한다. 즉, $\Delta D_n = f_\phi (n)$이며, 여기서 $\phi$는 디코더의 파라미터이다. 개별 픽셀에서 residual depth를 업데이트하는 대신 디코더 파라미터 $\phi$를 수정하여 최적화를 수행한다. 이렇게 하면 residual depth가 부드러워지고 최적화 중에 물체 표면이 일관되게 변형된다.

그러나 물체 사이에는 선명한 깊이 불연속성이 존재하기 때문에 디코더가 이를 처리하는 데 어려움을 겪는다. 저자들은 각 이미지를 각각 유사한 깊이를 갖는 $C = 5$개의 별도 영역으로 나누어 $C$채널 segmentation mask를 얻음으로써 이를 해결하였다. 구체적으로, Depth Anything을 사용하여 monocular depth를 추정하고 3D Moments의 전략을 따라 입력 깊이를 기반으로 이미지를 $C$개의 영역으로 나눈다. 이 경우 디코더는 $C$채널의 residual depth를 생성한다. 최종 residual depth는

\[\begin{equation} \Delta D_n = \textrm{chsum} (\mathbf{S} \odot f_\phi (n)) \end{equation}\]

으로 얻는다. (chsum: channelwise summation)

멀티 뷰 제약조건

단일 뷰 제약조건은 각 이미지에 해당하는 Gaussian의 부드러운 변형을 보장하지만, 모든 이미지에 의해 형성된 3D 표면이 부드러워지도록 강제하지는 않는다. 따라서 재구성된 형상이 부드러워지도록 하기 위해 렌더링된 깊이에 total variation (TV) 정규화 \(\mathcal{L}_\textrm{TV}\)를 사용한다. 구체적으로, rasterizer에서 색상 $\mathbf{c}$를 깊이 $d$로 대체하여 각 뷰에서 렌더링된 깊이 \(R_{\Sigma, \alpha, \mathbf{x}, d}\)를 얻는다. 그런 다음 다음과 같이 두 가지 방법으로 렌더링된 disparity (1/깊이)에 TV loss를 적용한다.

\[\begin{aligned} \mathcal{L}_\textrm{TV} &= \bigg\| \nabla \bigg( \frac{1}{1 + R_{\Sigma, \alpha, \mathbf{x}, d}} \bigg) \bigg\|_1 \\ \mathcal{L}_\textrm{MTV} &= \bigg\| \nabla \bigg( \mathbf{S} \odot \bigg( \frac{1}{1 + R_{\Sigma, \alpha, \mathbf{x}, d}} \bigg) \bigg) \bigg\|_1 \end{aligned}\]

여기서 \(\mathcal{L}_\textrm{TV}\)는 깊이가 전반적으로 부드럽도록 강제하는 반면, \(\mathcal{L}_\textrm{TV}\)는 각 분할된 영역의 깊이가 부드럽도록 보장한다. \(\mathcal{L}_\textrm{TV}\)를 최소화하여 글로벌하게 부드럽고 연결된 형상을 얻고 점진적으로 \(\mathcal{L}_\textrm{MTV}\)의 기여도를 높여 구조적 디테일을 개선한다.

\[\begin{equation} \mathcal{L}_\textrm{multi} = (1 - \lambda_s) \mathcal{L}_\textrm{TV} + \lambda_s \mathcal{L}_\textrm{MTV} \end{equation}\]

여기서 \(\lambda_s\)는 0으로 초기화되고 최적화가 끝날 때까지 점진적으로 증가하여 1에 도달한다.

2. Additional Regularization


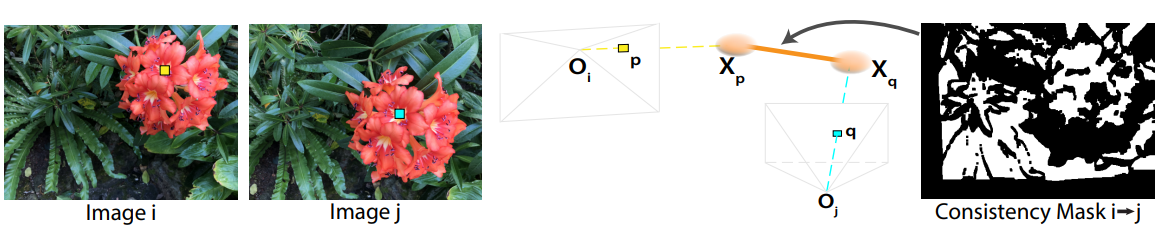
문제를 더욱 제한하기 위해 flow 기반 정규화 항을 사용한다. 핵심 아이디어는 두 입력 이미지의 대응되는 2D 포인트가 동일한 3D 포인트에서 나온다는 것이다. 따라서 두 이미지의 해당 픽셀의 Gaussian 위치가 유사하도록 강제한다.

\[\begin{equation} \mathcal{L}_\textrm{flow} = \sum_{(i,j)} \sum_{\mathbf{p}} \bigg\| M_{i \leftarrow j} \odot \bigg( g (D_i [\mathbf{p}], \mathbf{p}) - g (D_j [\mathbf{q}], \mathbf{q}) \bigg) \bigg\|_1 \\ \textrm{where} \quad D_i [\mathbf{p}] = D_i^\textrm{init} [\mathbf{p}] + \Delta D_i [\mathbf{p}] \end{equation}\]

$\mathbf{p}$와 $\mathbf{q}$는 각각 카메라 $i$와 $j$의 대응되는 픽셀이며, Flowformer++를 사용하여 계산된다. 또한, \(M_{i \leftarrow j}\)는 forward-backward consistency check를 사용하여 얻은 신뢰할 수 있는 대응 관계를 나타내는 바이너리 마스크이다.

요약하자면, 일관된 3D Gaussian 최적화는 다음 목적 함수를 최소화함으로써 수행된다.

\[\begin{equation} \Sigma^\ast, \phi^\ast, \mathbf{c}^\ast = \underset{\Sigma, \phi, \mathbf{c}}{\arg \min} \sum_{\mathbf{p} \in \mathcal{P}} \mathcal{L} (R_{\Sigma, \alpha, \mathbf{x}, \mathbf{c}} (\mathbf{p}), R (\mathbf{p})) + \beta_m \mathcal{L}_\textrm{multi} + \beta_f \mathcal{L}_\textrm{flow} \end{equation}\]

(\(\beta_m = 5\), \(\beta_f = 0.1\))

Gaussian의 불투명도 $\alpha$와 위치 $\mathbf{x}$는 디코더 파라미터 $\phi$를 업데이트하여 간접적으로 최적화된다.

3DGS는 각 픽셀의 중심만 샘플링하여 목적 함수를 최적화하지만, 이 전략은 sparse한 입력의 경우 Gaussian은 각 픽셀의 중심 색상과 일치하도록 변형되어 나머지 영역은 덮이지 않는다. 결과적으로 새로운 뷰에서 볼 때 표면은 반투명하게 보인다. 이 문제를 해결하기 위해 각 픽셀 내에서 여러 샘플에서 최적화를 수행한다. 다중 샘플링은 Gaussian이 각 픽셀을 적절히 덮도록 보장하여 이미지가 상당히 향상된다.

3. 3D Gaussian Initialization


정규화된 최적화 파이프라인을 용이하게 하기 위해 적절한 초기화가 필요하다. 특히, 최적화에는 초기 깊이 추정치 $D^\textrm{init}$이 필요하며, Depth Anything을 사용하여 이를 수행한다. Depth Anything은 고품질 depth map을 생성하지만 추정된 깊이는 상대적이며 종종 서로 다른 뷰에서 일관되지 않는다. 따라서 Depth Anything을 사용하여 초기화를 수행하면 위 그림의 왼쪽과 같이 다른 뷰에서 동일한 표면에 해당하는 Gaussian이 상당한 정렬 오차를 보여 최적화 프로세스를 방해한다.

이 문제를 완화하기 위해, 앞서 설명한 것과 유사한 flow 기반 loss를 사용한다. 그러나 깊이를 직접 최적화하면 flow가 정확한 영역에만 loss가 적용되고 나머지 영역의 깊이는 변경되지 않으므로 문제가 될 수 있다. 따라서 각 이미지에서 깊이의 scale과 offset만 최적화한다.

\[\begin{equation} \mathbf{s}^\ast, \mathbf{o}^\ast = \underset{\mathbf{s}, \mathbf{o}}{\arg \min} \sum_{(i,j)} \sum_{\mathbf{p}} \bigg\| M_{i \leftarrow j} \odot \bigg( g (s_i \cdot D_i^m [\mathbf{p}] + o_i, \mathbf{p}) - g (s_j \cdot D_j^m [\mathbf{q}] + o_j, \mathbf{q}) \bigg) \bigg\|_1 \end{equation}\]

($D_i^m$은 카메라 $i$에서의 monocular depth)

최적화가 완료되면 각 depth map에 대한 최적의 scale과 offset을 얻고, 이 scale과 offset을 monocular depth에 적용하여 초기 깊이를 얻을 수 있다.

\[\begin{equation} D^\textrm{init} = s \cdot D^m + o \end{equation}\]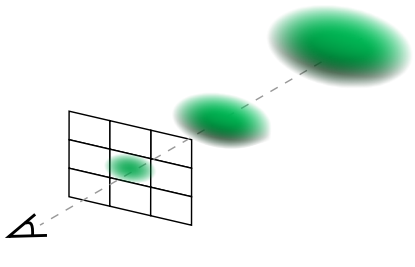


3DGS를 따라 공분산 행렬을 rotation matrix와 scale matrix로 표현한다. Rotation matrix는 항등 행렬로 초기화된다. Scale matrix의 경우, Gaussian을 구로 취급하며, 각 Gaussian이 해당 픽셀을 적절히 커버하도록 초기 깊이에 따라 scale을 계산한다.

\[\begin{equation} r = f \cdot D^\textrm{init} / H \end{equation}\]

여기서 $r$은 구의 반지름이며 $f$는 높이 $H$를 갖는 입력 이미지의 수직 초점 거리이다.

Experiments

  • 구현 디테일
    • optimizer: Adam
    • coarse alignment: 1k iteration
    • 최적화: 13k iteration
      • 처음 5k iteration에서는 rotation matrix을 항등 행렬로 고정하고 깊이에 따라 scale 할당
      • 나머지 8k iteration에서는 rotation matrix와 scale matrix를 자유롭게 최적화

1. Comparisons

다음은 LLFF 데이터셋에서 2~4개의 입력 뷰에 대한 재구성 결과를 기존 방법들과 비교한 것이다. (정성적 비교는 입력 뷰 3개)


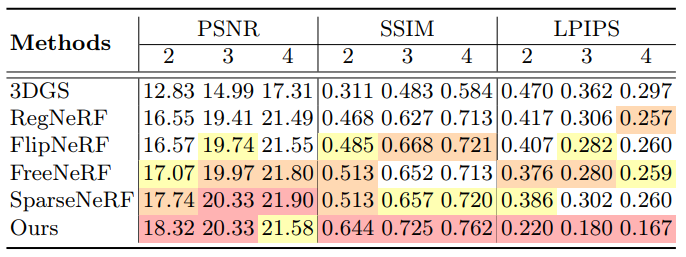
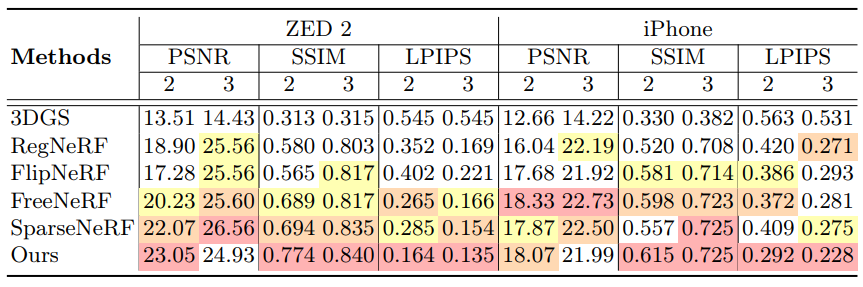
다음은 NVS-RGBD 데이터셋에서 2~3개의 입력 뷰에 대한 재구성 결과를 기존 방법들과 비교한 것이다. (정성적 비교는 입력 뷰 3개)

2. Ablations

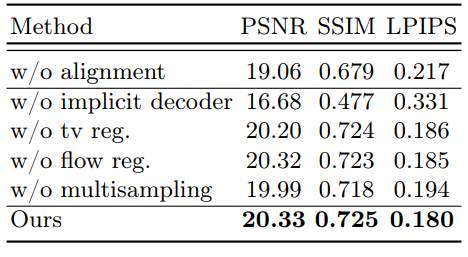
다음은 ablation 결과이다.

Limitations


  1. 각 픽셀에 Gaussian 1개를 할당하기 때문에 투명한 물체가 있는 장면을 처리하는 데 어려움이 있다.
  2. Monocular depth에 의존하기 때문에 깊이가 매우 부정확하면 합리적인 결과를 생성하지 못할 수도 있다.

You may also enjoy