[논문리뷰] DETRs with Collaborative Hybrid Assignments Training (Co-DETR)

ICCV 2023. [Paper] [Github]
Zhuofan Zong, Guanglu Song, Yu Liu
SenseTime Research
22 Nov 2022

Introduction

Object detection은 개체를 localize하고 해당 카테고리를 분류해야 하는 컴퓨터 비전의 기본 task이다. 중요한 R-CNN과 ATSS, RetinaNet, FCOS, PAA와 같은 일련의 변형 모델들은 object detection task의 획기적인 발전을 이끌었다. 일대다 레이블 할당은 이들의 핵심 방식이며, 각 ground-truth 박스는 proposal, 앵커, window center와 협력하는 supervised 타겟으로 detector 출력의 여러 좌표에 할당된다. 유망한 성능에도 불구하고 이러한 detector는 non-maximum suppression (NMS) 절차 또는 앵커 생성과 같은 수작업으로 설계된 많은 구성 요소에 크게 의존한다. 보다 유연한 end-to-end detector를 위해 DEtection TRansformer (DETR)이 제안되어 object detection을 집합 예측 문제로 보고 transformer 인코더-디코더 아키텍처를 기반으로 일대일 집합 매칭 방식을 도입하였다. 이러한 방식으로 각 ground-truth 박스는 하나의 특정 query에만 할당되며 사전 지식을 인코딩하는 여러 수작업으로 설계된 구성 요소는 더 이상 필요하지 않다. 이 접근 방식은 유연한 detection 파이프라인을 도입하고 많은 DETR 변형이 이를 더욱 개선하도록 권장한다. 그러나 바닐라 end-to-end object detector의 성능은 여전히 일대다 레이블 할당을 사용하는 기존 detector보다 좋지 못하다.

본 논문에서는 end-to-end 장점을 유지하면서 기존의 detector보다 우수한 DETR 기반 detector를 만들려고 하였다. 이 문제를 해결하기 위해 덜 positive한 query를 탐색하는 일대일 집합 매칭의 직관적인 단점에 중점을 두었다. 이것은 심각한 비효율적인 학습 문제로 이어질 것이다. 저자들은 인코더에서 생성된 latent 표현과 디코더에서 attention 학습이라는 두 가지 측면에서 이를 자세히 분석하였다.

먼저 Deformable-DETR과 디코더를 ATSS 헤드로 간단히 대체한 일대다 레이블 할당 방법 사이의 latent feature의 discriminability score (식별 가능성 점수)를 비교하였다. 각 공간 좌표의 feature $\ell^2$-norm은 discriminability score를 나타내는 데 사용된다. 인코더의 출력 $\mathcal{F} \in \mathbb{R}^{C \times H \times W}$가 주어지면 discriminability score map $\mathcal{S} \in \mathbb{R}^{1 \times H \times W}$를 얻을 수 있다. 해당 영역의 score가 높을수록 개체를 더 잘 감지할 수 있다.

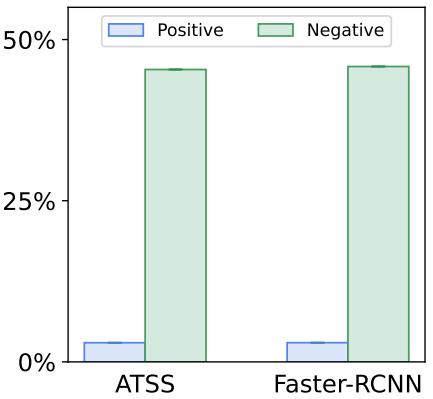
Discriminability score에 다른 임계값을 적용하여 IoF-IoB 곡선 (IoF: 전경 교차, IoB: 배경 교차)을 그릴 수 있다. ATSS의 경우 더 높은 IoF-IoB 곡선을 보이며, 이는 전경과 배경을 구별하기가 더 쉽다는 것을 나타낸다. $\mathcal{S}$를 시각화하면 일대다 레이블 할당 방법에서는 일부 salient 영역의 feature가 완전히 활성화되지만 일대일 집합 매칭에서는 덜 탐색된다는 것을 알 수 있다. 저자들은 디코더 학습을 탐색하기 위해 Deformable-DETR과 Group-DETR을 기반으로 디코더에서 cross-attention 주의 점수의 IoF-IoB 곡선을 그려 더 positive한 query를 디코더에 도입하였다. 디코더에서 너무 적은 positive query는 attention 학습에 영향을 미치고 더 많은 positive query를 증가시키면 이를 약간 완화할 수 있다.

이 중요한 관찰은 저자들이 간단하지만 효과적인 공동 하이브리드 할당 학습 방식 (Co-DETR)을 제시하도록 동기를 부여하였다. Co-DETR의 핵심 통찰력은 다목적 일대다 레이블 할당을 사용하여 인코더와 디코더 모두의 학습 효율성과 효과를 개선하는 것이다. 보다 구체적으로, 보조 head를 transformer 인코더의 출력과 통합한다. 이러한 head는 ATSS, FCOS, Faster RCNN 과 같은 다목적 일대다 레이블 할당으로 supervise할 수 있다. 서로 다른 레이블 할당은 인코더 출력에 대한 supervision을 강화하여 이러한 head의 학습 수렴을 지원하기에 충분히 discriminative하다. 디코더의 학습 효율성을 더욱 향상시키기 위해 positive anchor와 positive proposal을 포함하여 이러한 보조 head에서 positive sample의 좌표를 정교하게 인코딩한다. 사전 할당된 카테고리와 boundary box를 예측하기 위해 여러 positive query 그룹으로 원래 디코더에 전송된다. 각 보조 head의 positive 좌표는 다른 그룹과 격리된 독립 그룹 역할을 한다. 다재다능한 일대다 레이블 할당은 디코더의 학습 효율성을 향상시키기 위해 (positive query, ground-truth) 쌍을 도입할 수 있다. 원래 디코더만 inference 중에 사용되므로 제안된 학습 방식은 학습 중에 추가 오버헤드만 도입한다.

Method

1. Overview

표준 DETR 프로토콜에 따라 입력 이미지가 backbone과 인코더에 공급되어 latent feature를 생성한다. 여러 사전 정의된 object query는 나중에 cross-attention을 통해 디코더에서 상호 작용한다. Co-DETR을 도입하여 인코더의 feature 학습과 디코더의 attention 학습을 공동 하이브리드 할당 학습 방식과 맞춤형 positive query 생성을 통해 개선한다.

2. Collaborative Hybrid Assignments Training

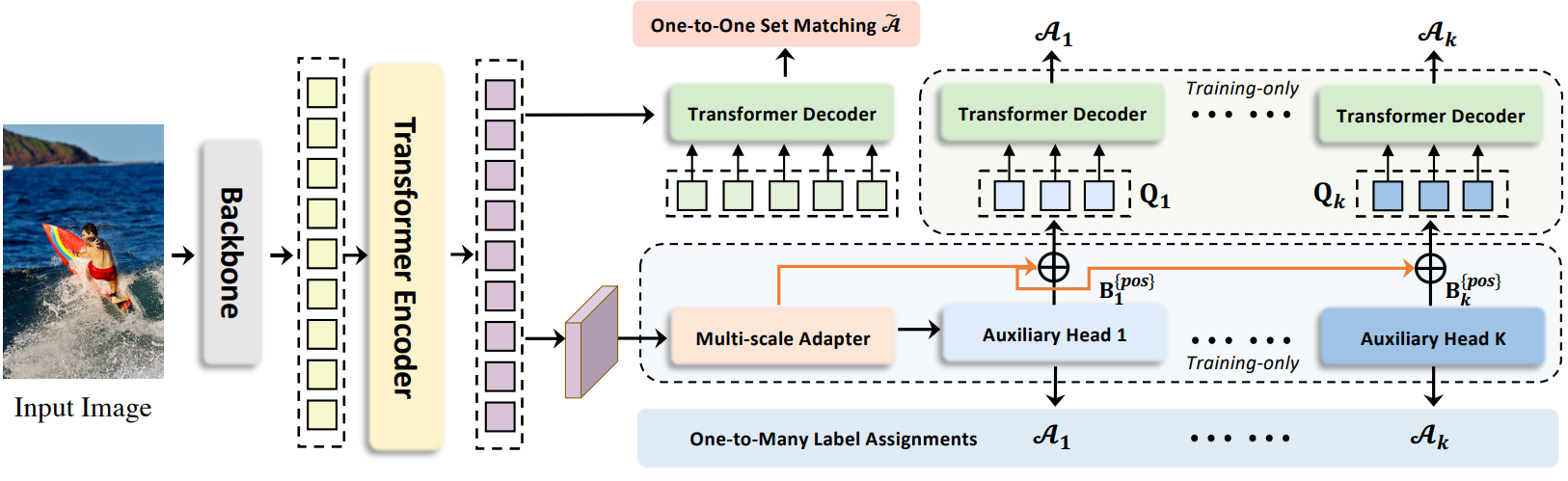
디코더에서 적은 수의 positive query로 인해 발생하는 인코더 출력에 대한 희박한 supervision을 완화하기 위해 다양한 일대일 레이블 할당 패러다임 (ex. ATSS, Faster R-CNN)이 있는 다목적 보조 head를 통합한다. 서로 다른 레이블 할당은 인코더 출력에 대한 supervision을 강화하여 이러한 head의 학습 수렴을 지원하기에 충분히 discriminative하다. 특히, 인코더의 latent feature $\mathcal{F}$가 주어지면 먼저 멀티스케일 어댑터를 통해 feature pyramid \(\{\mathcal{F}_1, \cdots, \mathcal{F}_J\}\)로 변환한다. 여기서 $J$는 $2^{2+J}$ 다운샘플링 stride가 있는 feature map을 나타낸다. ViTDet와 유사하게 feature pyramid는 단일 스케일 인코더의 단일 feature map으로 구성되는 반면 업샘플링에는 bilinear interpolation과 3$\times$3 convolution을 사용한다. 예를 들어, 인코더의 단일 스케일 feature를 사용하여 다운샘플링 (stride 2의 3$\times$3 convolution) 또는 업샘플링 연산을 연속적으로 적용하여 feature pyramid를 생성한다. 멀티스케일 인코더의 경우 멀티스케일 인코더 feature $\mathcal{F}$에서 가장 coarse한 feature만 다운샘플링하여 feature pyramid를 구축한다. 정의된 $K$개의 협업 head는 해당 레이블 할당 방식 \(\mathcal{A}_k\)와 $i$번째 협업 head에 대해 \(\{\mathcal{F}_1, \cdots, \mathcal{F}_J\}\)가 전송되어 예측 \(\hat{P}_i\)를 얻는다. $i$번째 head에서 \(\mathcal{A}_i\)는 $P_i$의 positive sample과 negative sample에 대한 supervised 타겟을 계산하는 데 사용된다. $G$를 ground-truth 집합이라 하면 이 절차는 다음과 같이 공식화할 수 있다.

\[\begin{equation} P_i^{\{\textrm{pos}\}}, B_i^{\{\textrm{pos}\}}, P_i^{\{\textrm{neg}\}} = \mathcal{A}_i (\hat{P}_i, G) \end{equation}\]

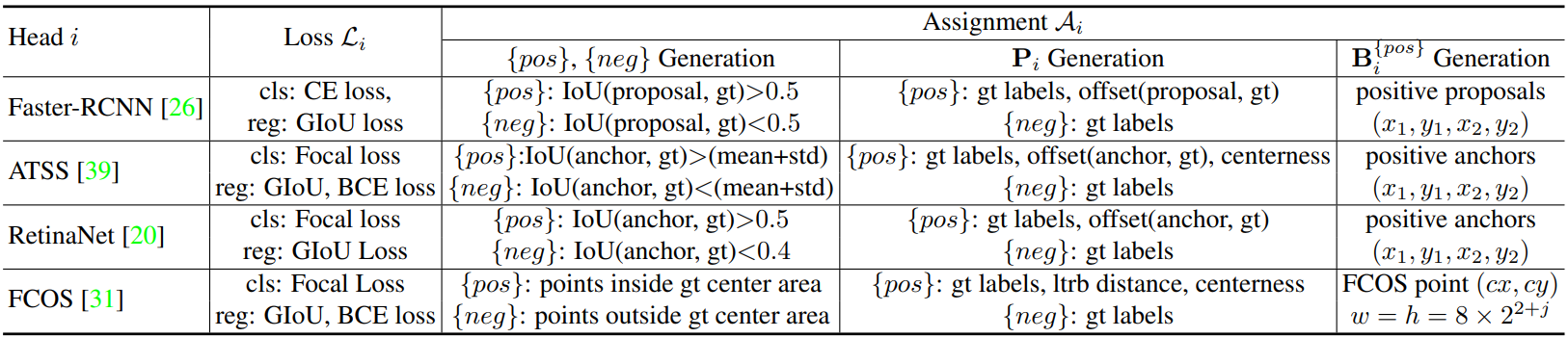
여기서 \(\{\textrm{pos}\}\)와 \(\{\textrm{neg}\}\)는 \(\mathcal{A}_i\)에 의해 결정된 ($j$, \(\mathcal{F}_j\)에서의 positive 또는 negative 좌표) 쌍의 집합이다. $j$는 feature 인덱스이다. \(B_i^{\{\textrm{pos}\}}\)는 공간적 positive 좌표의 집합이다. \(P_i^{\{\textrm{pos}\}}\)와 \(P_i^{\{\textrm{neg}\}}\)는 해당 좌표의 supervised 타겟들이며, 카테고리와 회귀 오프셋을 포함한다. 구체적으로 각 변수에 대한 자세한 정보는 아래 표와 같다.

Loss function은 다음과 같이 정의할 수 있다.

\[\begin{equation} \mathcal{L}_i^\textrm{enc} = \mathcal{L}_i (\hat{P}_i^\textrm{\{\textrm{pos}\}}, P_i^{\{\textrm{pos}\}}) + \mathcal{L}_i (\hat{P}_i^\textrm{\{\textrm{neg}\}}, P_i^{\{\textrm{neg}\}}) \end{equation}\]

Negative sample의 경우 regression loss가 무시된다. $K$개의 보조 head에 대한 최적화의 목적 함수는 다음과 같다.

\[\begin{equation} \mathcal{L}^\textrm{enc} = \sum_{i=1}^K \mathcal{L}_i^\textrm{enc} \end{equation}\]

3. Customized Positive Queries Generation

일대일 집합 매칭 패러다임에서 각 ground-truth 박스는 supervised 타겟으로 하나의 특정 query에만 할당된다. Positive query가 너무 적으면 transformer 디코더에서 비효율적인 cross-attention 학습이 발생한다. 이를 완화하기 위해 각 보조 head의 레이블 할당 \(\mathcal{A}_i\)에 따라 충분한 맞춤형 positive query를 정교하게 생성한다. 구체적으로, $i$번째 보조 head에서 positive 좌표 집합 \(B_i^{\{\textrm{pos}\}} \in \mathbb{R}^{M_i \times 4}\) ($M_i$는 positive sample의 수)가 주어지면 추가 맞춤형 positive query $Q_i \in \mathbb{R}^{M_i \times C}$는 다음과 같이 생성될 수 있다.

\[\begin{equation} Q_i = \textrm{Linear} (\textrm{PE} (B_i^{\{\textrm{pos}\}})) + \textrm{Linear} (\textrm{E} (\{\mathcal{F}_\ast\}, \{\textrm{pos}\})) \end{equation}\]

여기서 $\textrm{PE} (\cdot)$는 positional encoding을 나타내며 인덱스 쌍 ($j$, \(\mathcal{F}_j\)의 positive 좌표 negative 좌표)에 따라 $\textrm{E} (\cdot)$에서 해당 feature를 선택한다.

결과적으로 단일 일대일 집합 매칭 분기에 기여하는 $K + 1$개의 query 그룹과 학습 중에 일대다 레이블 할당이 있는 $K$개의 분기가 있다. 보조 일대다 레이블 할당 분기는 원래 기본 분기의 $L$개의 디코더 레이어와 동일한 파라미터를 공유한다. 보조 분기의 모든 query는 positive query로 간주되므로 매칭 프로세스가 폐기된다. $i$번째 보조 분기에서 $l$번째 디코더 레이어의 loss는 다음과 같이 공식화될 수 있다.

\[\begin{equation} \mathcal{L}_{i, l}^{\textrm{dec}} = \tilde{\mathcal{L}} (\tilde{P}_{i, l}, P_i^{\{\textrm{pos}\}}) \end{equation}\]

\(\tilde{P}_{i, l}\)은 $i$번째 보조 분기에서 $l$번째 디코더 레이어의 출력 예측을 나타낸다. 마지막으로 Co-DETR의 목적 함수는 다음과 같다.

\[\begin{equation} \mathcal{L}^\textrm{global} = \sum_{l=1}^L (\tilde{\mathcal{L}}_l^\textrm{dec} + \lambda_1 \sum_{i=1}^K \mathcal{L}_{i, l}^\textrm{dec} + \lambda_2 \mathcal{L}^\textrm{enc}) \end{equation}\]

여기서 \(\tilde{\mathcal{L}}_l^\textrm{dec}\)는 원래 일대일 집합 매칭 분기의 loss이며, $\lambda_1$과 $\lambda_2$는 loss들의 균형을 맞추는 계수들이다.

4. Why Co-DETR works

Co-DETR은 DETR 기반 detector를 확실히 개선한다. 저자들은 그 효과를 정성적, 정량적으로 조사하였다. 구체적으로 36-epoch 설정을 사용하여 ResNet50 backbone을 사용하여 Deformable-DETR 기반으로 상세 분석을 수행하였다.

인코더의 supervision 강화

직관적으로 positive query가 너무 적으면 각 ground-truth에 대한 regression loss에 의해 하나의 query만 supervise되므로 supervision이 희박해진다. 일대다 레이블 할당 방식의 positive sample은 latent feature 학습을 향상시키는 데 도움이 되는 더 많은 localization supervision을 받는다. 저자들은 희박한 supervision이 모델 학습을 방해하는 방법을 자세히 알아보기 위해 인코더에서 생성된 latent feature를 자세히 조사하였다. 인코더 출력의 discriminability score를 양자화하기 위해 IoF-IoB 곡선을 도입하였다 (IoF: 전경 교차, IoB: 배경 교차).

특히 인코더의 latent feature $\mathcal{F}$가 주어지면 IoF와 IoB를 계산하였다. 레벨 $j$에서 인코더의 feature \(\mathcal{F}_j \in \mathbb{R}^{C \times H_j \times W_j}\)가 주어지면 먼저 $\ell^2$-norm \(\hat{\mathcal{F}}_j \in \mathbb{R}^{1 \times H_j \times W_j}\)를 계산하고 이미지 크기 H$\times$W로 resize한다. Discriminability score $\mathcal{D}(\mathcal{F})$는 다음과 같이 모든 레벨의 score를 평균하여 계산한다.

\[\begin{equation} \mathcal{D} (\mathcal{F}) = \frac{1}{J} \sum_{j=1}^J \frac{\hat{\mathcal{F}}_j}{\max (\hat{\mathcal{F}}_j)} \end{equation}\]

여기서 resize 연산은 생략되었다.

위 그림은 ATSS, Deformable-DETR, Co-Deformable-DETR의 discriminability score를 시각화한 것이다. Deformable-DETR과 비교할 때 ATSS와 Co-Deformable-DETR은 모두 주요 객체의 영역을 구별하는 더 강력한 능력을 가지고 있지만 Deformable-DETR은 배경에 의해 거의 방해를 받는다.

결과적으로 저자들은 전경과 배경에 대한 지표를 각각

\[\begin{equation} \unicode{x1D7D9} (\mathcal{D} (\mathcal{F}) > S) \in \mathbb{R}^{H \times W}, \quad \unicode{x1D7D9} (\mathcal{D} (\mathcal{F}) < S) \in \mathbb{R}^{H \times W} \end{equation}\]

로 정의하였다. $S$는 미리 정의된 score 임계값이며, $\unicode{x1D7D9}(x)$는 $x$가 참이면 1이고 그렇지 않으면 0이다. 전경 마스크 $\mathcal{M}^{\textrm{fg}} \in \mathbb{R}^{H \times W}$의 경우 \(\mathcal{M}_{h,w}^{\textrm{fg}}\)는 점 $(h, w)$가 전경 내부에 있으면 1이고 그렇지 않으면 0이다. 전경 교차 영역 (IoF) $\mathcal{I}^{\textrm{\textrm{fg}}}$는 다음과 같이 계산할 수 있다.

\[\begin{equation} \mathcal{I}^{\textrm{fg}} = \frac{\sum_{h=1}^H \sum_{w=1}^W \unicode{x1D7D9} (\mathcal{D} (\mathcal{F}_{h,w} > S) \cdot \mathcal{M}_{h,w}^\textrm{fg})}{\sum_{h=1}^H \sum_{w=1}^w \mathcal{M}_{h,w}^\textrm{fg}} \end{equation}\]

유사한 방식으로 배경 영역(IoB)에 대한 교차 영역을 계산한다.

위 그림은 $S$를 변경하여 IoF-IoB 곡선을 plot한 것이다. ATSS와 Co-Deformable-DETR은 동일한 IoB 값에서 Deformable-DETR과 Group-DETR보다 더 높은 IoF 값을 얻는다. 이는 인코더 표현이 갖는 일대다 레이블 할당의 이점을 보여준다.

Hungarian 매칭의 불안정성을 줄여 cross-attention 학습을 개선

Hungarian 매칭은 일대일 집합 매칭의 핵심이다. Cross-attention은 positive query가 풍부한 개체 정보를 인코딩하는 데 도움이 되는 중요한 task이다. 이를 위해서는 충분한 학습이 필요하다. 동일한 이미지의 특정 positive query에 할당된 ground-truth 정보가 학습 과정 중에 변경되기 때문에 Hungarian 매칭은 제어할 수 없는 불안정성을 도입한다.

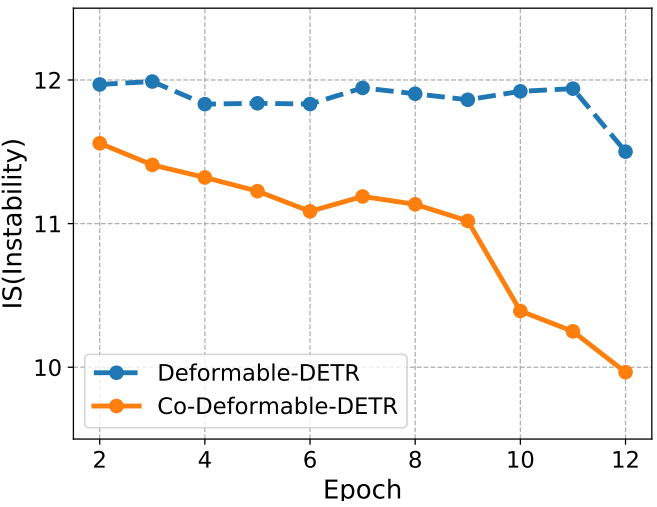
위 그림은 불안정성에 대한 비교를 제시한다. 본 논문의 접근 방식이 보다 안정적인 매칭 프로세스에 기여한다는 것을 알 수 있다. 또한 cross-attention이 얼마나 잘 최적화되고 있는지 정량화하기 위해 attention score에 대한 IoF-IoB 곡선도 계산한다. 저자들은 discriminability score 계산과 유사하게 attention score에 대해 서로 다른 임계값을 설정하여 여러 IoF-IoB 쌍을 얻었다.

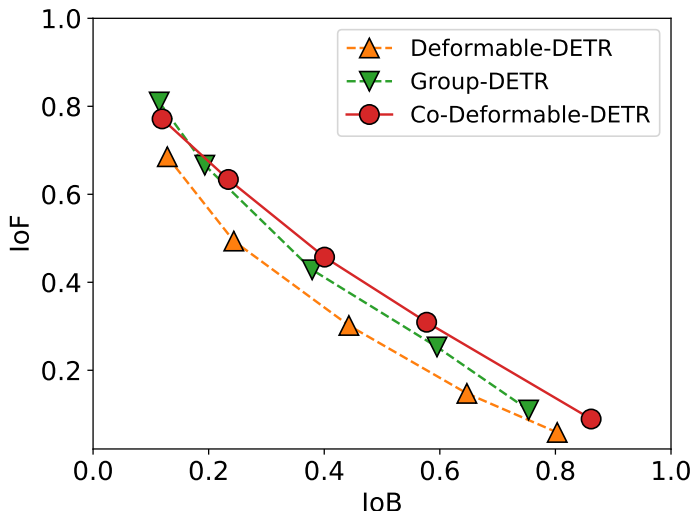
Deformable-DETR, Group-DETR, Co-Deformable-DETR 사이의 비교는 위 그림에서 볼 수 있다. 보다 positive한 query가 있는 DETR의 IoF-IoB 곡선은 일반적으로 Deformable-DETR보다 높다.

5. Comparison with other methods

본 논문의 방법과 다른 방버들의 차이점

Group-DETR, H-DETR, SQR은 중복된 그룹과 반복된 ground-truth 박스의 일대일 매칭을 통해 일대다 할당을 수행한다. Co-DETR은 여러 공간 좌표를 각 ground-truth에 대한 positive로 명시적으로 할당한다. 따라서 이러한 조밀한 supervision 신호는 latent feature map에 직접 적용되어 더 식별할 수 있다. 반대로 Group-DETR, H-DETR, SQR에는 이 메커니즘이 없다. 더 positive한 query가 이러한 상대에 도입되었지만 Hungarian 매칭에 의해 구현된 일대다 할당은 여전히 일대일 매칭의 불안정성 문제로 어려움을 겪고 있다.

본 논문의 방법은 기존 일대다 할당의 안정성으로부터 이점을 얻고 positive query와 ground-truth 박스 사이의 특정 매칭 방식을 상속한다. Group-DETR과 H-DETR은 일대일 매칭과 기존의 일대다 할당 사이의 상보성을 밝히지 못한다. 본 논문은 전통적인 일대다 할당과 일대일 매칭을 사용하여 detector에 대한 정량적 및 정성적 분석을 최초로 제공하였다. 이를 통해 차이점과 보완성을 더 잘 이해할 수 있으므로 추가로 전문화된 일대다 디자인 경험 없이 기존 일대다 할당 디자인을 활용하여 DETR의 학습 능력을 자연스럽게 향상시킬 수 있다.

디코더에 negative query가 도입되지 않는다.

중복된 object query는 필연적으로 디코더에 대한 많은 양의 negative query와 GPU 메모리의 상당한 증가를 가져온다. 그러나 본 논문의 방법은 디코더에서 positive 좌표만 처리하므로 메모리를 덜 사용한다.

Experiments

• 데이터셋: MS COCO 2017
• 구현 디테일
  • DETR과 같은 파이프라인에 Co-DETR을 통합하고 학습 세팅을 동일하게 유지
  • 보조 head: $K = 2$인 경우 ATSS와 Faster-RCNN를 적용, $K = 1$의 경우 ATSS만 적용
  • 학습 가능한 object query 수: 300
  • $\lambda_1$ = 1.0, $\lambda_2$ = 2.0
  • Co-Deformable-DETR++의 경우 copy-paste와 soft-NMS를 사용한 대규모 jitter를 사용

1. Main Results

다음은 Deformable-DETR++에 대한 실험 결과이다.

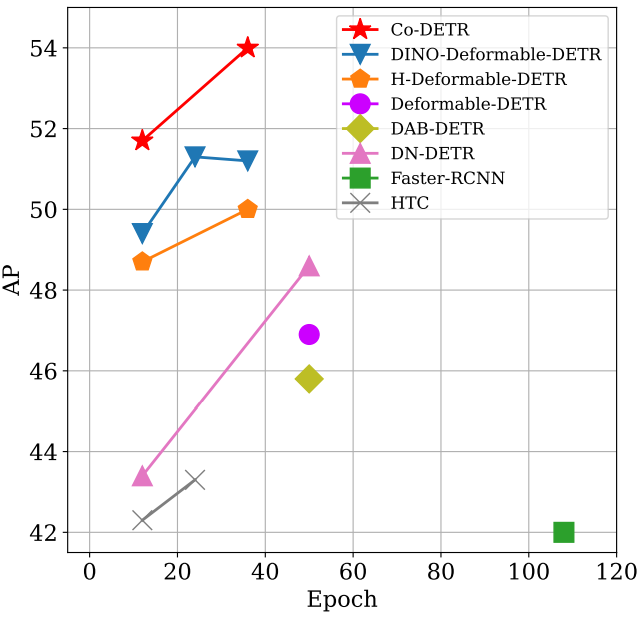
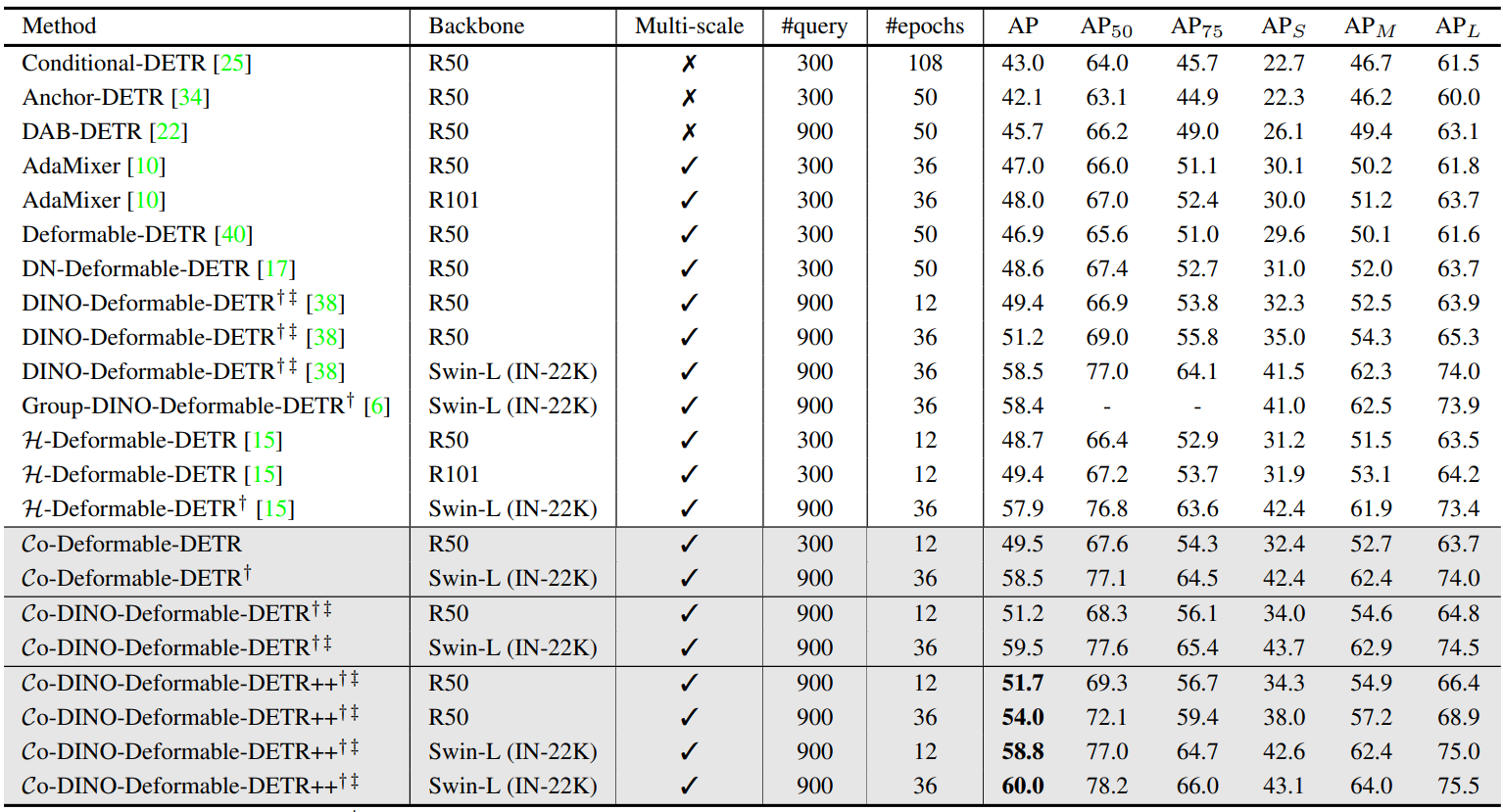
2. Comparisons with the state-of-the-art

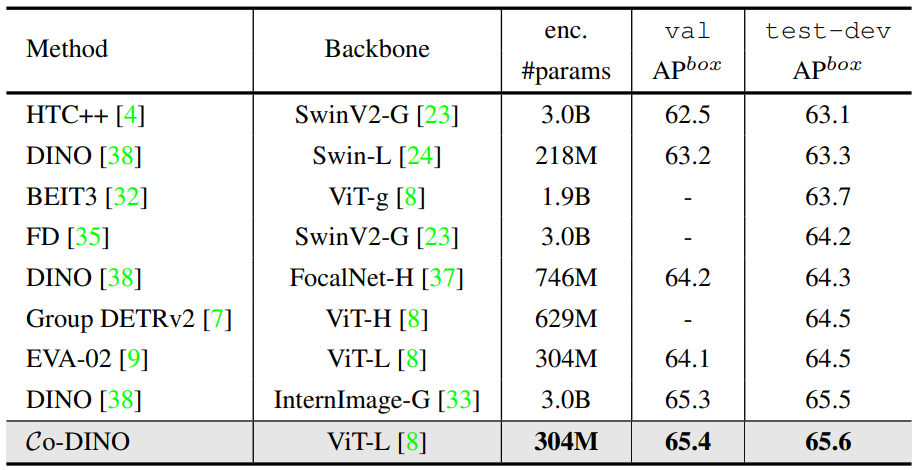
다음은 COCO val 데이터셋에서 SOTA DETR 변형들과 비교한 표이다.

다음은 COCO test-dev 데이터셋에서 SOTA 프레임워크들과 비교한 표이다.

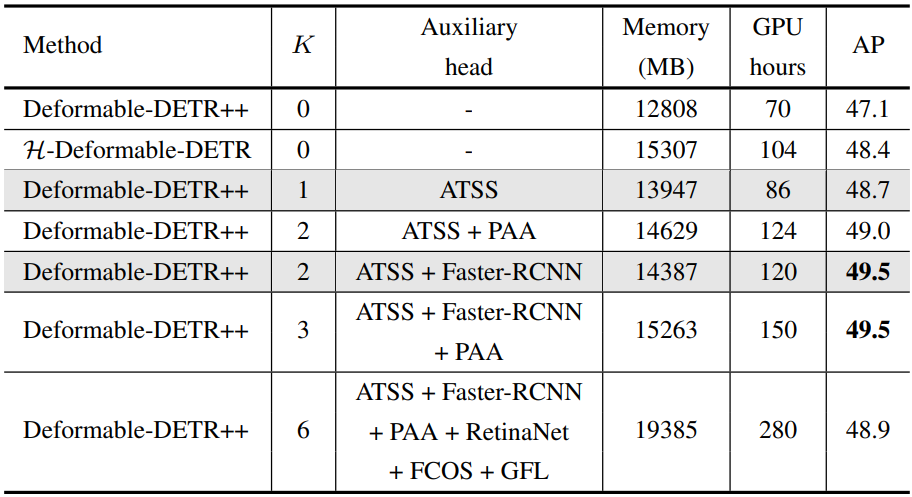
3. Ablation Studies

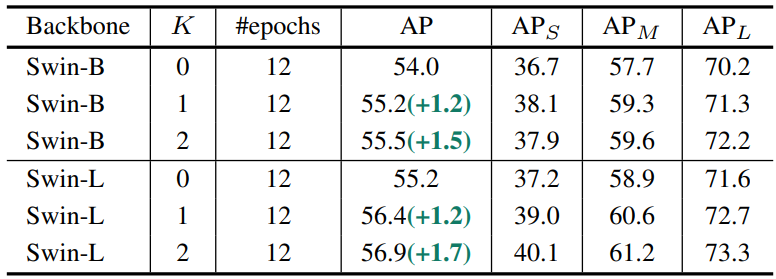
다음은 $K$의 개수에 따른 실험 결과이다.

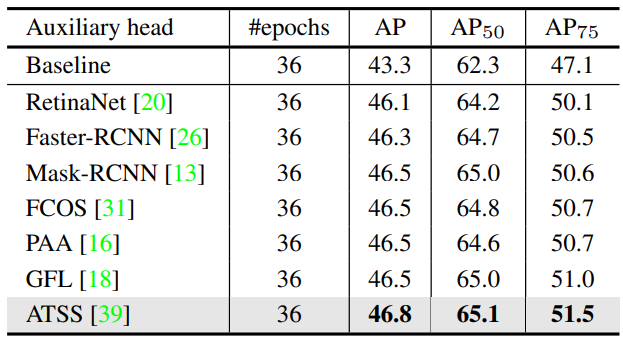
다음은 COCO val 데이터셋에서 다양한 보조 head에 대한 성능을 비교한 표이다.

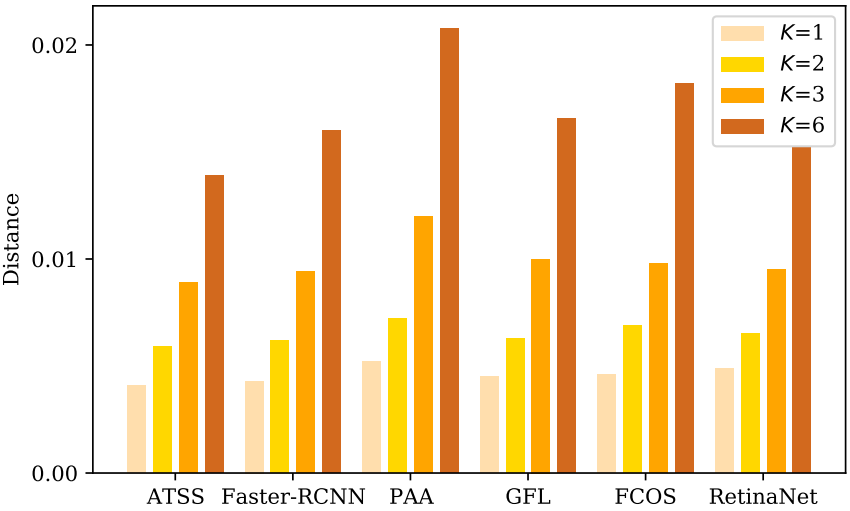
동일한 공간 좌표가 다른 전경 박스에 할당되거나 다른 보조 head에서 배경으로 처리될 때 충돌이 발생하여 detector의 학습에 혼동을 줄 수 있다. 저자들은 먼저 다음과 같이 head $H_i$와 head $H_j$ 사이의 거리를 정의하고 $H_i$의 평균 거리로 최적화 충돌을 측정하였다.

\[\begin{equation} \mathcal{S}_{i, j} = \frac{1}{\vert D \vert} \sum_{I \in D} \textrm{KL} (\mathcal{C} (H_i (I)), \mathcal{C} (H_j (I))) \\ \mathcal{S}_i = \frac{1}{2(K-1)} \sum_{j \ne i}^K (\mathcal{S}_{i,j} + \mathcal{S}_{j,i}) \end{equation}\]

여기서 $\textrm{KL}$, $D$, $I$, $\mathcal{C}$는 각각 KL divergence, 데이터셋, 입력 이미지, class activation maps (CAM)을 뜻한다.

다음은 다양한 $K$에 대한 거리를 비교한 그래프이다.

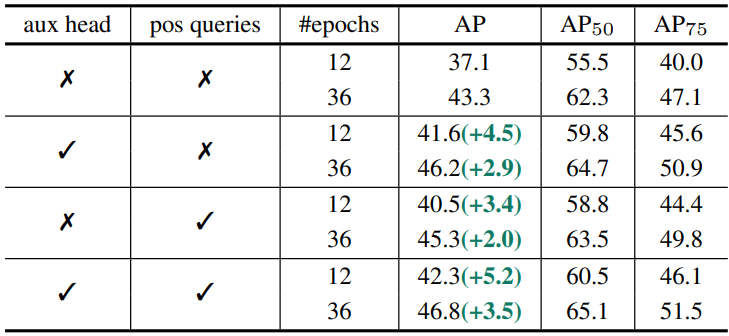
다음은 요소별 ablation 결과이다.

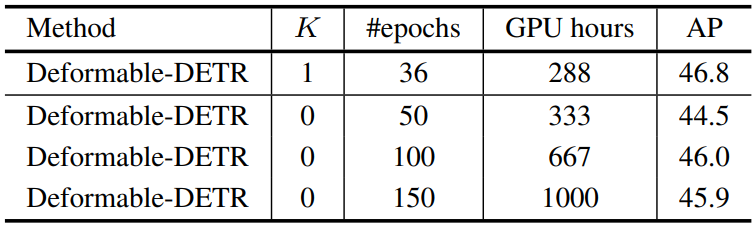
다음은 더 긴 학습 schedule과의 비교한 표이다.

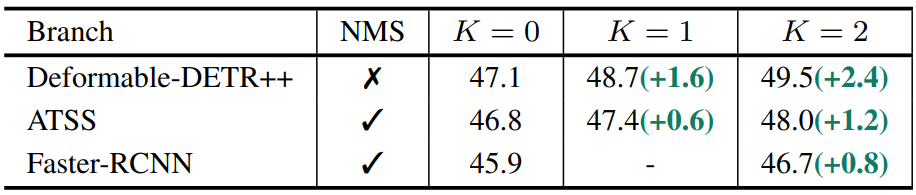
다음은 보조 분기의 성능을 비교한 표이다.

다음 그림은 원래 query와 맞춤형 query의 분포를 비교한 것이다. 빨간색 점은 디코더에서 Hungarian 매칭으로 할당한 positive query들이고, 파란색 점과 주황색 점은 각각 Faster-RCNN과 ATSS에 의해 추출된 positive query들이다.

다음은 원래 query들과 맞춤형 query들 사이의 정규화된 거리를 측정한 표이다.