[논문리뷰] Click-Gaussian: Interactive Segmentation to Any 3D Gaussians

ECCV 2024. [Paper] [Page]
Seokhun Choi, Hyeonseop Song, Jaechul Kim, Taehyeong Kim, Hoseok Do
LG Electronics | Seoul National University
16 Jul 2024

Introduction

최근에는 렌더링 효율성 향상, 재구성 품질 향상 등 3DGS의 장점을 활용하여 3DGS 기반의 다양한 segmentation 방법이 제안되었다. 일부 방법들은 Segment Anything Model (SAM)과 같은 foundation model의 semantic 표현에 맞춰 3D Gaussian의 feature field를 학습시켰다. 이 접근 방식을 사용하면 3D feature field를 통해 3D 장면을 명시적으로 분할할 수 있다. 그러나 이 방법은 장면에서 구별 가능한 feature field를 학습하는 데 어려움을 겪으며 명확한 segmentation을 위해서는 광범위한 후처리가 필요하다. 시간이 많이 걸리는 후처리는 3DGS의 효율성 이점을 크게 방해한다.

다른 방법들은 object tracking 메커니즘을 활용하여 SAM 기반 세그먼트 ID를 사전 할당함으로써 3D segmentation을 해결하였다. 그러나 이 방법은 object tracking 결과에 의존하며 추적되지 않은 물체는 segmentation 프로세스에서 제외될 수 있다.

이러한 고려 사항들은 광범위한 후처리 없이 구별 가능한 feature field를 제공하는 3D segmentation 방법을 탐색하는 데 동기를 부여하였다. 이러한 기술의 발전은 3D 장면과의 실시간 상호 작용을 크게 향상시켜 3D 물체 조작 시 보다 직관적이고 반응성이 뛰어난 경험을 가능하게 할 수 있다. 또한 3D 장면 편집 능력을 향상시킬 뿐만 아니라 다양한 분야에 걸쳐 3D 장면 표현의 실제 적용 범위를 넓힐 수 있는 잠재력을 가지고 있다.

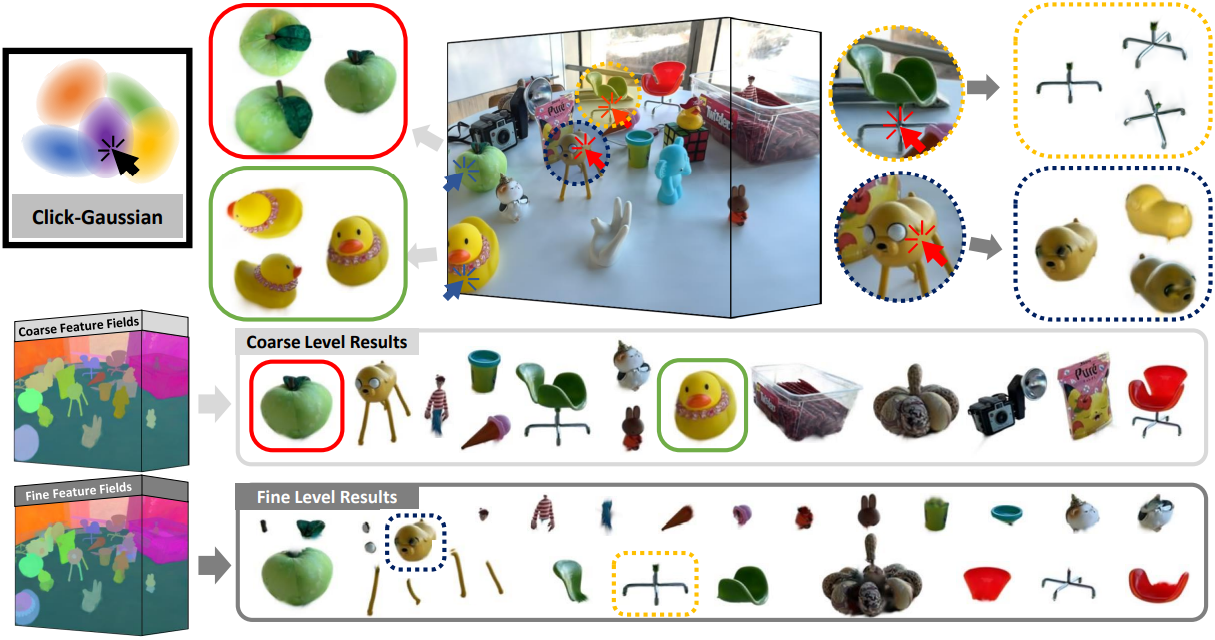
본 논문에서는 실제 장면에서 사전 학습된 3D Gaussian의 interactive segmentation을 위한 실용적이고 효율적인 방법으로 Click-Gaussian을 제안하였다. SAM에서 추출된 2D segmentation mask를 활용하여 2단계 세분성, 즉 coarse-level과 fine-level의 feature로 3D Gaussian의 feature를 풍부하게 만들어 세밀한 분할을 촉진한다. 2단계 세분성을 통해 3D 환경에서 다양한 스케일로 장면 요소를 캡처하여 segmentation 결과의 정밀도와 디테일을 향상시킬 수 있다. 이는 SAM의 2D segmentation mask를 기반으로 하는 contrastive learning을 통해 Gaussian feature에 대한 세분성 prior를 통합함으로써 달성된다.

이 프로세스의 중요한 장애물은 다양한 뷰에서 2D 마스크의 불일치로 인해 일관되고 구별 가능한 semantic feature의 학습을 방해한다는 것이다. 이 문제를 해결하기 위해 학습 뷰 전반에 걸쳐 global feature 후보를 체계적으로 집계하여 3D feature field의 개발을 일관되게 알리는 새로운 전략인 Global Feature-guided Learning (GFL)을 도입한다. GFL은 feature 학습의 견고성과 신뢰성을 향상시켜 개별 2D segmentation mask에 존재하는 고유한 모호성의 영향을 완화한다.

Methods

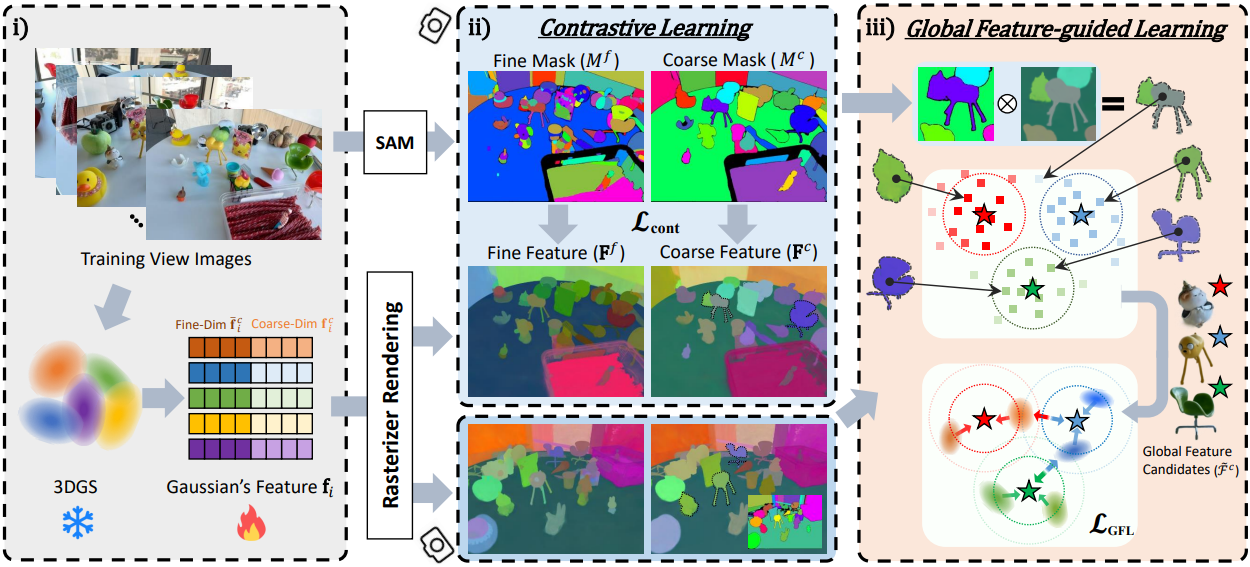
1. Feature Fields of Click-Gaussian

Click-Gaussian은 장면의 각 3D Gaussian에 segmentation을 위한 추가 feature를 장착하여 작동한다. 구체적으로, 3D Gaussian $g_i$가 주어지면 각 Gaussian은 3D segmentation을 위해 $D$차원 feature 벡터 \(\textbf{f}_i \in \mathbb{R}^D\)가 추가되어 \(\tilde{g}_i = g_i \cup \{\textbf{f}_i\}\)가 된다.

저자들은 \(\textbf{f}_i\)를 \(\textbf{f}_i^c \in \mathbb{R}^{D^c}\)와 \(\bar{\textbf{f}}_i^c \in \mathbb{R}^{D-D^c}\)로 나누어 coarse-level 마스크와 fine-level 마스크 모두에서 feature를 잘 학습할 수 있도록 했다. 저자들은 \(\textbf{f}_i^c\)를 coarse-level feature로 사용하고, \(\textbf{f}_i^f = \textbf{f}_i^c \oplus \bar{\textbf{f}}_i^c\)를 fine-level feature로 사용한다. 여기서 $\oplus$는 concatenatation이다. 이를 통해 fine-level feature의 학습을 더욱 효과적으로 만든다.

Rasterizer를 사용하면 색상을 렌더링할 때와 유사하게 픽셀에서 2레벨 feature \(\textbf{F}^l\)을 계산할 수 있다.

\[\begin{equation} \textbf{F}^l = \sum_{i \in \mathcal{N}} \textbf{f}_i^l \alpha_i T_i \end{equation}\]

여기서 \(l = \{f, c\}\)는 세분성 레벨이다. 각 픽셀의 2레벨 feature 계산은 한 번의 forward pass로 수행된다.

2. contrastive Learning

Cosine similarity 기반의 contrastive learning을 사용하여 2레벨 마스크 세트로 구별되는 feature들을 학습시킨다. 학습 이미지 $I \in \mathcal{I}$에 대한 2레벨 마스크를 \(M^l \in \mathcal{M}\)라 하자. 픽셀 $p_1$과 $p_2$에 대하여 마스크 값이 동일하면 (\(M_{p_1}^l = M_{p_2}^l\)) 렌더링된 feature 간의 cosine similarity를 최대화하는 것을 목표로 한다.

\[\begin{equation} \mathcal{L}_\textrm{pos}^\textrm{cont} = - \frac{1}{\vert P_1 \vert \vert P_2 \vert} \sum_l^{\{f, c\}} \sum_{p_1}^{P_1} \sum_{p_2}^{P_2} \unicode{x1D7D9} [M_{p_1}^l = M_{p_2}^l] \, \textbf{S}^l (p_1, p_2) \end{equation}\]

여기서 $P_1$과 $P_2$는 샘플링된 픽셀들이며, $\vert \cdot \vert$는 집합의 원소 수이다. \(\textbf{S}^l (p_1, p_2) = \langle \textbf{F}_{p_1}^l, \textbf{F}_{p_2}^l \rangle\)는 두 픽셀의 렌더링된 feature 사이의 cosine similarity이다. 반대로, 서로 다른 마스크 값을 갖는 픽셀의 경우 (\(M_{p_1}^l \ne M_{p_2}^l\)) 렌더링된 feature의 cosine similarity가 $\tau^l$을 초과하지 않도록 제한한다.

\[\begin{equation} \mathcal{L}_\textrm{neg}^\textrm{cont} = \frac{1}{\vert P_1 \vert \vert P_2 \vert} \sum_l^{\{f, c\}} \sum_{p_1}^{P_1} \sum_{p_2}^{P_2} \unicode{x1D7D9} [M_{p_1}^l \ne M_{p_2}^l] \, \unicode{x1D7D9} [\textbf{S}^l (p_1, p_2) > \tau^l] \, \textbf{S}^l (p_1, p_2) \end{equation}\]

두 점이 fine-level에서는 별개의 부분을 나타내지만 coarse-level에서는 동일한 물체일 수 있기 때문에 fine-level feature에 대한 negative contrastive loss를 최적화하는 동안 coarse-level feature에 stop gradient 연산 $\textrm{sg}$를 적용한다.

\[\begin{equation} \textbf{F}^f = \textrm{sg}(\textbf{F}^c) \oplus \bar{\textbf{F}}^c \end{equation}\]

이 방법은 fine-level에서 구별하는 데 중요한 요소에 대한 학습 프로세스에 효과적으로 초점을 맞춘다.

전체 contrastive loss는 다음과 같다.

\[\begin{equation} \mathcal{L}_\textrm{cont} = \mathcal{L}_\textrm{pos}^\textrm{cont} + \lambda_\textrm{neg}^\textrm{cont} \mathcal{L}_\textrm{neg}^\textrm{cont} \end{equation}\]

여기서 \(\lambda_\textrm{neg}^\textrm{cont}\)는 hyperparameter이다.

3. Global Feature-guided Learning

Click-Gaussian의 feature들은 contrastive learning을 통해 학습되었음에도 불구하고 학습 뷰에서 SAM 마스크의 불일치로 인해 문제에 직면한다. 이 문제는 각 시점에서 마스크를 독립적으로 사용하기 때문에 발생하며 잠재적으로 신뢰할 수 없는 학습 신호로 이어질 수 있다. 이를 해결하기 위해 저자들은 지속적으로 global feature 후보를 획득하는 방법인 Global Feature-guided Learning (GFL)을 제안하였다.

Global feature 후보

지정된 수의 학습 iteration 후에 모든 학습 뷰에서 각 2레벨 마스크의 평균 feature를 계산한다. 이는 2D feature map을 렌더링하고 모든 학습 뷰의 각 마스크에 average pooling을 적용하여 수행된다.

레벨 $l$에서 시점 $v$에 대한 마스크를 $M^{l,v} \in \mathbb{Z}^{H \times W}$, 학습 뷰의 수를 $V$라 하면, 평균 feature는 다음과 같이 계산된다.

\[\begin{equation} \mathcal{F}^l = \bigg\{ \bar{F}_s^{l,v} \in \mathbb{R}^{D^l} \, \vert \, \bar{F}_s^{l,v} = \frac{1}{\vert \mathcal{P}_s^{l,v} \vert} \sum_{p \in \mathcal{P}_s^{l,v}} \textbf{F}_p^{l,v}, \; 1 \le s \le \max_v M^{l,v} \bigg\} \end{equation}\]

여기서, \(\mathcal{P}_s^{l,v} = \{p \; \vert \; M_p^{l,v} = s \}\)는 마스크 $M^{l,v}$에서 동일한 세그먼트 ID를 갖는 픽셀 집합이고 $D^l$은 레벨 $l$의 feature 차원이다. Inference 시 3DGS의 실시간 렌더링 속도 덕분에 이러한 average pooling 절차는 기울기 계산 없이 빠르게 수행된다. 그런 다음 HDBSCAN 클러스터링 알고리즘을 각 세트 \(\mathcal{F}^l\)에 적용하여 장면 전반에 걸쳐 각 레벨에 대한 $C^l$개의 global feature 후보 \(\tilde{\mathcal{F}}^l\)을 얻는다. 이러한 global feature 후보는 최신 global feature를 얻기 위해 정기적으로 업데이트된다. 특히, 이러한 global cluster는 모든 뷰에 걸쳐 잡음이 있는 2D segment에서 렌더링된 feature를 그룹화하여 파생되므로 전체 장면의 가장 대표적인 feature가 되어 SAM 마스크의 불일치를 효과적으로 완화한다.

Global Feature-guided Learning

Global feature 후보는 뷰에 일관된 방식으로 Click-Gaussian을 학습시킬 수 있게 해준다. Gaussian feature \(\textbf{f}_i^l\)의 경우 해당 feature가 특정 global cluster에 속하고 다른 cluster와 멀리 떨어지도록 가이드한다. 여기에는 $i$번째 Gaussian feature가 레벨 $l$에 속할 가능성이 가장 높은 cluster ID인 $c_i^l$를 식별하는 작업이 포함된다.

\[\begin{equation} c_i^l = \underset{c}{\arg \max} \; \tilde{\textbf{S}}^l (i, c) \end{equation}\]

여기서 \(\tilde{\textbf{S}}^l (i, c) = \langle \textbf{f}_i^l, \tilde{\mathcal{F}}_c^l \rangle\)는 $i$번째 Gaussian feature와 ID가 $c$인 global cluster feature 간의 cosine similarity이다. 가장 가능성이 높은 global cluster에 속하는 Gaussian feature을 supervise하기 위한 GFL loss는 다음과 같이 정의된다.

\[\begin{equation} \mathcal{L}_\textrm{pos}^\textrm{GFL} = - \frac{1}{N} \sum_l^{\{f,c\}} \sum_i^N \unicode{x1D7D9} [\tilde{\textbf{S}}^l (i, c_i^l) > \tau^g] \, \tilde{\textbf{S}}^l (i, c_i^l) \end{equation}\]

여기서 $\tau^g$는 cluster에 속할지 여부를 결정하는 threshold이다. 반대로, Gaussian feature를 다른 global cluster에서 벗어나게 하는 GFL loss는 다음과 같이 정의된다.

\[\begin{equation} \mathcal{L}_\textrm{neg}^\textrm{GFL} = \frac{1}{N} \sum_l^{\{f,c\}} \sum_i^N \frac{1}{C^l} \sum_{c \ne c_i^l}^{C^l} \unicode{x1D7D9} [\tilde{\textbf{S}}^l (i, c) > \tau^l] \, \tilde{\textbf{S}}^l (i, c) \end{equation}\]

따라서 총 GFL loss는 다음과 같다.

\[\begin{equation} \mathcal{L}_\textrm{GFL} = \mathcal{L}_\textrm{pos}^\textrm{GFL} + \mathcal{L}_\textrm{neg}^\textrm{GFL} \end{equation}\]

Global cluster를 사용하여 Gaussian feature에 GFL loss를 직접 적용하면 정확한 3D segmentation에 필수적인 안정적인 supervision을 통해 식별력과 잡음에 대한 견고성이 향상된다.

4. Regularization

Hypersphere 정규화

지나치게 큰 norm을 가진 feature는 다른 feature의 참여를 과소평가하여 모든 Gaussian feature의 효과적인 학습을 방해한다. 하나의 Gaussian feature가 feature 렌더링의 알파 블렌딩 프로세스에서 지배적인 것을 방지하기 위해 Gaussian feature가 hypersphere 표면에 놓이도록 제한한다.

\[\begin{equation} \mathcal{L}_\textrm{3D-norm} = \frac{1}{N} \sum_{i=1}^N (\| \textbf{f}_i^c \|_2 - 1)^2 + (\| \bar{\textbf{f}}_i^c \|_2 - 1)^2 \end{equation}\]

렌더링된 feature 정규화

Hypersphere 정규화로 인해, 레벨 $l$의 각 Gaussian feature \(\textbf{f}_i\)는 반지름 $r^l$의 hypersphere 표면에 놓인다 ($r^c = 1$, $r^f = \sqrt{2}$). 그러나 서로 다른 방향의 feature 벡터가 렌더링 과정에서 통합되므로 렌더링된 feature의 norm \(\| \textbf{F}_p^l \|_2\)는 $r^l$보다 작다. 이는 하나의 픽셀에 대해 \(\textbf{F}_p^l\)에 기여하는 \(\textbf{f}_i\)가 다양할 수 있음을 의미한다. \(\textbf{F}_p^l\)의 렌더링에 기여하는 모든 \(\textbf{f}_i\)가 동일한 방향으로 정렬되도록 하기 위해 렌더링된 feature에 다음 정규화를 적용한다.

\[\begin{equation} \mathcal{L}_\textrm{2D-norm} = \frac{1}{HW} \sum_{l}^{\{f,c\}} \sum_p^{HW} (\| \textbf{F}_p^l \|_2 - r^l)^2 \end{equation}\]

공간적 일관성 정규화

3D 공간 정보를 활용하여 근접한 Gaussian이 유사한 feature를 나타내도록 한다. 학습 초기에 공간적으로 근접한 이웃에 대한 효율적인 쿼리를 용이하게 하기 위해 Gaussian의 3D 위치를 사용하여 KD-tree를 구성한다. 학습 과정 전반에 걸쳐 $N_s$개의 Gaussian들을 샘플링하고 3D 공간에서 $K$개의 nearest neighbor의 feature와 일치하도록 feature를 조정한다.

\[\begin{equation} \mathcal{L}_\textrm{spatial} = - \frac{1}{N_s K} \sum_i^{N_s} \sum_k^K \langle \textbf{f}_i, \textbf{f}_k \rangle \end{equation}\]

여기서 $\langle \cdot, \cdot \rangle$는 cosine similarity이다.

Click-Gaussian 학습의 전체 loss는 다음과 같다.

\[\begin{equation} \mathcal{L}_\textrm{total} = \mathcal{L}_\textrm{cont} + \lambda_1 \mathcal{L}_\textrm{GFL} + \lambda_2 \mathcal{L}_\textrm{3D-norm} + \lambda_3 \mathcal{L}_\textrm{2D-norm} + \lambda_4 \mathcal{L}_\textrm{spatial} \end{equation}\]

여기서 \(\lambda_1\), \(\lambda_2\), \(\lambda_3\), \(\lambda_4\)는 각 loss 항의 균형을 맞추는 hyperparameter들이다.

Experiments

• 구현 디테일
  • feature를 제외한 Gaussian의 다른 파라미터들은 모두 고정
  • $D_c$ = 12, $D$ = 24
  • $\tau^f$ = 0.75, $\tau^c$ = 0.5, $\tau^g$ = 0.9
  • $N_s$ = 100,000, $K$ = 5
  • \(\lambda_\textrm{neg}^\textrm{cont}\) = 0.1, \(\lambda_1\) = 10.0, \(\lambda_2\) = 0.2, \(\lambda_3\) = 0.2, \(\lambda_4\) = 0.5
  • optimizer: Adam
  • learning rate: 0.01
  • iteration: 3,000
    • GFL은 2,000번째 iteration부터 통합
  • contrastive learning 시에는 마스크 픽셀 수를 기반으로 한 중요도 샘플링을 사용하여 각 학습 iteration마다 10,000개의 픽셀을 샘플링
  • HDBSCAN
    • epsilon: coarse-level feature는 $1 \times 10^{-2}$, fine-level feature는 $1 \times 10^{-3}$
    • 최소 cluster 크기는 학습 뷰 수에 비례
  • NVIDIA RTX A5000 GPU 1개에서 약 13분 소요

1. Comparisons

다음은 LERF-Mask 데이터셋에서 baseline들과 비교한 결과이다.

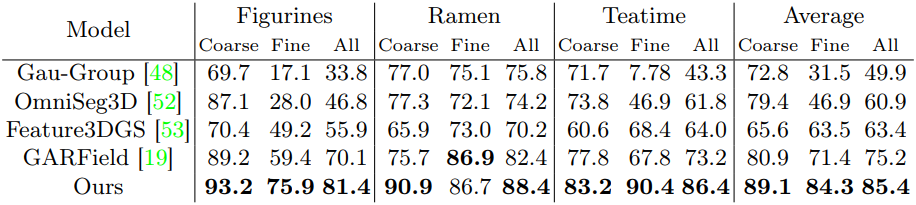
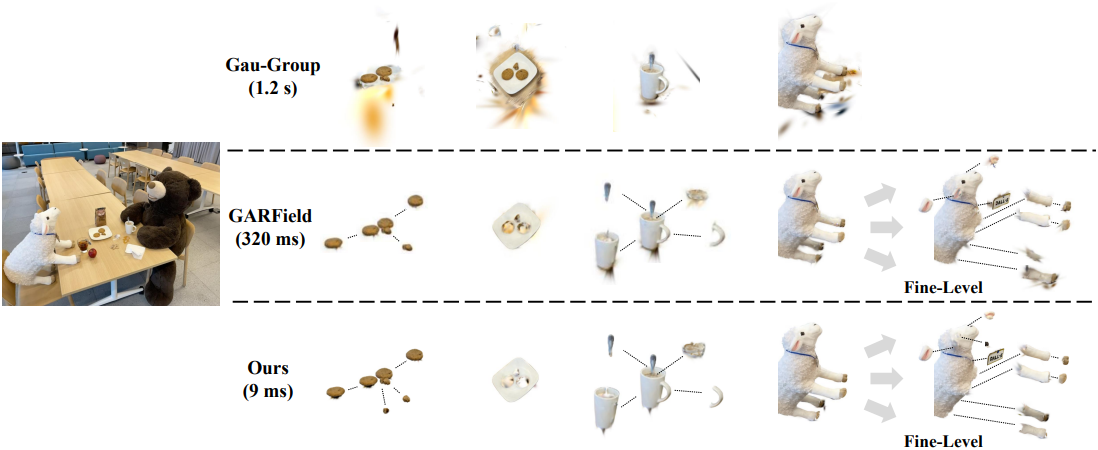
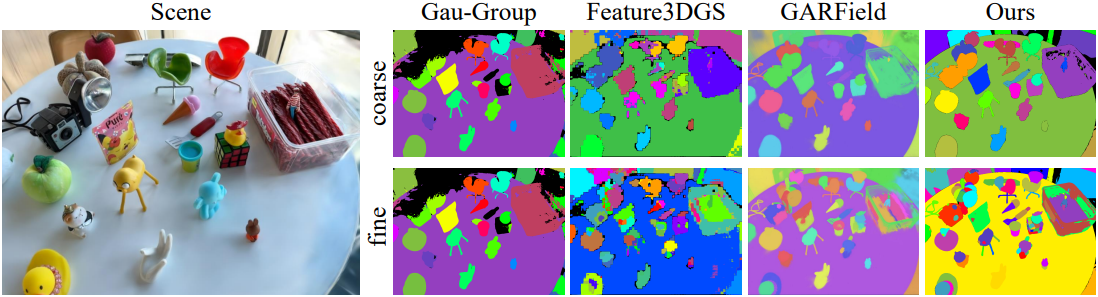
다음은 Gau-Group, GARField, SAGA와의 비교 결과이다.

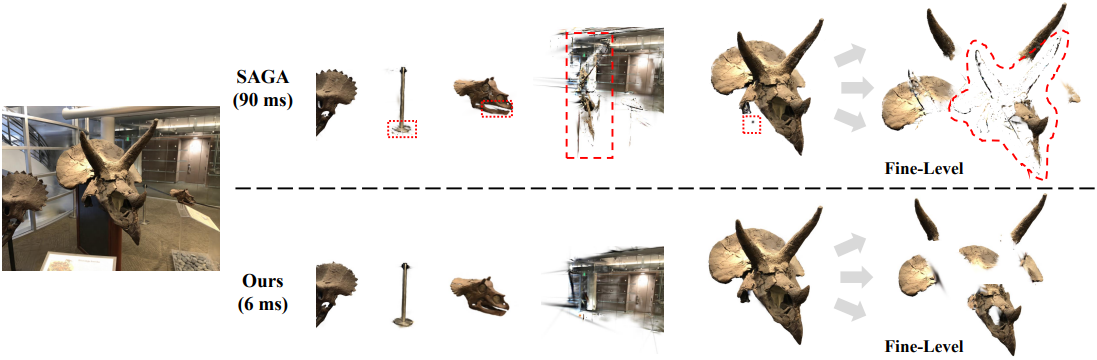
다음은 새로운 시점에서 모든 것을 분할한 결과를 비교한 것이다.

다음은 SPIn-NeRF 데이터셋에서 baseline들과 비교한 표이다.

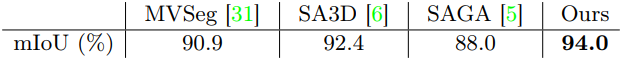
2. Ablation Study

다음은 각 구성 요소들에 대한 ablation 결과이다.

3. Versatile Applications

다음은 다양한 편집 예시이다. 텍스트 기반 편집은 CLIP 기반 편집 방법들을 사용하였으며, ‘flower’를 ‘stained glass flower’로 편집하였다.