[논문리뷰] CityGaussian: Real-time High-quality Large-Scale Scene Rendering with Gaussians

ECCV 2024. [Paper] [Page] [Github]
Yang Liu, He Guan, Chuanchen Luo, Lue Fan, Naiyan Wang, Junran Peng, Zhaoxiang Zhang
Chinese Academy of Sciences | University of Chinese Academy of Sciences | Centre for Artificial Intelligence and Robotic | Shandong University | TuSimple | University of Science and Technology Beijing
1 Apr 2024

Introduction

3D Gaussian Splatting (3DGS)에 대한 대부분의 기존 연구들은 주로 물체나 작은 장면에 초점을 맞춘다. 그러나 3DGS를 대규모 장면 재구성에 적용하면 학습하는 동안 GPU 메모리에 엄청난 오버헤드가 발생한다. 예를 들어, RTX3090 24G에서 Gaussian의 수가 1,100만 이상으로 증가하면 메모리 부족 오류가 발생한다. 그러나 공중에서 촬영한 1.5$\textrm{km}^2$가 넘는 도시를 높은 시각적 품질로 재구성하려면 2,000만 개가 넘는 Gaussian이 필요하다. 이러한 용량의 3DGS는 40G A100에서도 직접 학습할 수 없다.

반면, 렌더링 속도 병목 현상은 깊이 정렬에 있다. Gaussian의 수가 수백만 개로 증가함에 따라 rasterization이 매우 느려진다. 예를 들어, 110만 개의 Gaussian으로 구성된 Tanks&Temples 데이터셋의 기차 장면은 평균적으로 보이는 Gaussian의 수가 약 65만 개이고 속도는 103 FPS로 렌더링된다. 하지만 2,300만 개의 Gaussian으로 구성된 2.7$\textrm{km}^2$의 MatrixCity 장면은 평균적으로 보이는 Gaussian의 수가 약 65만 개임에도 불구하고 21 FPS의 속도로만 렌더링할 수 있다. 그리고 불필요한 Gaussian을 rasterization에서 제거하는 방법은 실시간 대규모 장면 렌더링의 핵심이다.

본 논문은 이 문제를 해결하기 위해 CityGaussian (CityGS)을 제안하였다. Mega-NeRF에서 영감을 얻어 분할 정복 전략을 채택하였다. 전체 장면을 먼저 block으로 분할하고 병렬로 학습시킨다. 각 block은 훨씬 적은 Gaussian으로 표현되고 적은 데이터로 학습되므로 메모리가 적게 사용된다. Gaussian 분할의 경우, 경계가 없는 장면을 정규화된 경계가 있는 정육면체로 축소시키고 균일한 그리드 분할을 적용한다. 학습 데이터 분할의 경우, 카메라가 해당 block 내부에 있거나 해당 block의 렌더링 결과에 상당한 기여를 하는 경우에만 보관한다. 이 새로운 전략은 Gaussian 소비를 줄여 더 높은 충실도를 구현하는 동시에 무관한 데이터로 인한 방해를 효율적으로 피한다. Block에서 학습된 Gaussian을 정렬하기 위해 각 block의 학습을 coarse한 global Gaussian prior로 가이드한다. 이 전략은 block 간의 간섭을 효율적으로 피하고 원활한 융합을 가능하게 한다.

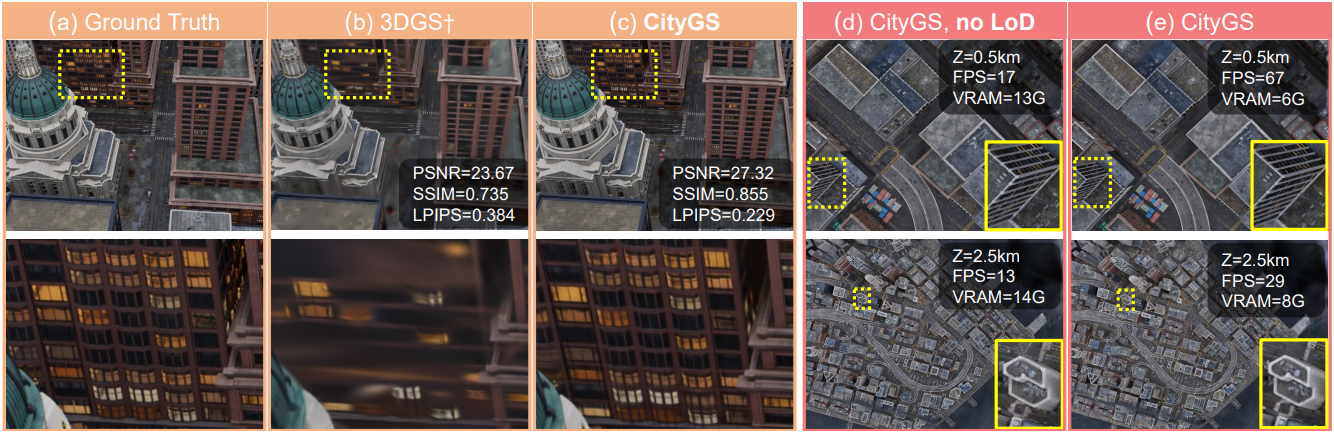
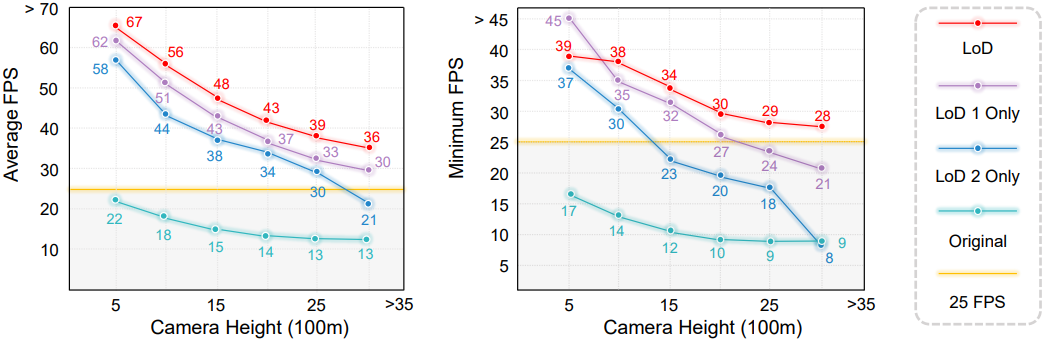
대규모의 Gaussian을 렌더링할 때 계산 부담을 덜기 위해 block별 Level-of-Detail (LoD) 전략을 사용한다. 핵심 아이디어는 필요한 Gaussian만 rasterizer에 공급하는 것이다. 구체적으로, 이전에 분할된 block을 단위로 사용하여 view frustum에 포함될 가능성이 있는 Gaussian을 빠르게 결정한다. 또한 원근 효과로 인해 먼 영역은 화면 공간의 작은 영역을 차지하고 디테일이 적다. 따라서 카메라에서 멀리 떨어진 Gaussian block을 압축 버전으로 대체하여 더 적은 Gaussian을 사용할 수 있다. 이런 방식으로 rasterizer의 처리 부담을 크게 줄여 엄청나게 큰 시야에서도 실시간 대규모 장면 렌더링을 유지할 수 있다.

Method

1. Training

Global Gaussian prior 생성

이 부분은 추가적인 Gaussian 분할과 데이터 분할의 기초 역할을 한다. 단순하게 COLMAP 포인트에 분할 정복 전략을 적용하면 깊이 제약과 글로벌한 인식이 부족하여 block 외부 영역을 overfitting하기 위해 floater가 많이 생성되어 서로 다른 block을 안정적으로 융합하기 어렵다. 또한 COLMAP 포인트에서 렌더링된 이미지는 흐릿하고 부정확하여 특정 뷰가 block 학습에 중요한지 여부를 평가하기 어렵다.

저자들은 이 문제를 해결하기 위해 간단하면서도 효과적인 방법을 제안하였다. COLMAP 포인트로 초기화한 다음 모든 학습 이미지에 대하여 30,000 iteration동안 학습시켜 coarse한 global Gaussian prior \(\textbf{G}_\textbf{K} = \{ G_k \vert k = 1, \ldots, K\}\)를 생성한다. 추가 block별 fine-tuning에서 \(\textbf{G}_\textbf{K}\)는 기하학적으로 적절한 위치를 가리키고, block 융합 시 간섭을 제거한다. 이 coarse한 Gaussian은 더 정확한 형상과 더 깨끗한 렌더링된 이미지를 제공하여 primitive와 데이터 분할을 용이하게 한다.

Primitive와 데이터 분할

대부분의 현실 장면에 경계가 없다는 점을 고려하면 최적화된 Gaussian은 무한대로 확장될 수 있다. 원래 3D 공간에 균일한 그리드 분할을 직접 적용하면 거의 빈 block이 많이 생겨서 작업 부하가 불균형해진다. 이 문제를 완화하기 위해 먼저 global Gaussian prior을 경계가 있는 정육면체 영역으로 수축시킨다.

내부 전경 영역, 즉 위 그림의 분홍색 사각형은 선형적으로 매핑되며, 외부 배경 영역은 비선형적으로 매핑된다. 구체적으로, 전경 영역의 코너 위치를 \(\textbf{p}_\textrm{min}\)과 \(\textbf{p}_\textrm{max}\)라고 하면, Gaussian의 위치를 다음과 같이 \([-1, 1]\) 사이로 정규화한다.

\[\begin{equation} \hat{\textbf{p}}_k = 2 \cdot \frac{\textbf{p}_k - \textbf{p}_\textrm{min}}{\textbf{p}_\textrm{max} - \textbf{p}_\textrm{min}} - 1 \end{equation}\]

그런 다음 다음과 같은 함수로 수축된다.

\[\begin{equation} \textrm{contract} (\hat{\textbf{p}}_k) = \begin{cases} \hat{\textbf{p}}_k & \quad \textrm{if} \; \| \hat{\textbf{p}}_k \|_\infty \le 1 \\ \bigg( 2 - \frac{1}{\| \hat{\textbf{p}}_k \|_\infty} \bigg) \frac{\hat{\textbf{p}}_k}{\| \hat{\textbf{p}}_k \|_\infty} & \quad \textrm{if} \; \| \hat{\textbf{p}}_k \|_\infty > 1 \\ \end{cases} \end{equation}\]

이 수축된 공간을 균등하게 분할함으로써, 더 균형 잡힌 Gaussian 분할이 가능하다.

Fine-tuning 단계에서는 각 block이 충분히 학습되기를 바란다. 구체적으로, 할당된 데이터는 block 내의 디테일을 정제하는 데 집중하여 학습되어야 한다. 따라서 고려된 block이 특정 뷰의 렌더링 결과에 상당히 많이 보이는 경우에만 그 뷰를 학습에 사용해야 한다. 심각하게 가려지거나 적게 기여하는 경우는 고려하지 않아야 한다. SSIM loss는 구조적 차이를 효율적으로 포착할 수 있고 어느 정도 밝기 변화에 민감하지 않기 때문에 데이터 분할 전략의 기반으로 삼는다.

구체적으로, $j$번째 block에 포함된 coarse한 global Gaussian은 다음과 같다.

\[\begin{equation} \textbf{G}_{\textbf{K}_j} = \{ G_k \; \vert \; \textbf{b}_{j, \textrm{min}} \le \textrm{contract} (\hat{\textbf{p}}_k) < \textbf{b}_{j, \textrm{max}}, k = 1, \ldots, K_j \} \end{equation}\]

여기서 \(\textbf{b}_{j, \textrm{min}}\)과 \(\textbf{b}_{j, \textrm{max}}\)는 block $j$의 $x, y, z$ 경계이고, $K_j$는 포함된 Gaussian의 수이다. 그러면 $i$번째 pose \(\tau_i\)가 $j$번째 block에 할당되는지 여부는 다음과 같이 결정된다.

\[\begin{equation} \textbf{B}_1 (\tau_i, \textbf{G}_{\textbf{K}_j}) = \begin{cases} 1 & \quad L_\textrm{SSIM} (I_{\textbf{G}_{\textbf{K}}} (\tau_i), I_{\textbf{G}_{\textbf{K}_j}} (\tau_i)) > \epsilon \\ 0 & \quad \textrm{otherwise} \end{cases} \end{equation}\]

Threshold $\epsilon$보다 큰 SSIM loss는 렌더링된 이미지에 block $j$가 상당히 기여함을 의미하므로 $\tau_i$를 block $j$에 할당한다.

그러나 이 원칙에만 의존하면 block 모서리에서 외부를 볼 때 아티팩트가 발생할 수 있다. 이러한 경우는 고려된 block의 projection과 거의 관련이 없기 때문에 첫 번째 원칙에 따라 충분히 학습되지 않는다. 따라서 block에 속하는 pose도 해당 block에 포함한다.

\[\begin{equation} \textbf{B}_2 (\tau_i, \textbf{G}_{\textbf{K}_j}) = \begin{cases} 1 & \quad \textbf{b}_{j, \textrm{min}} \le \textrm{contract} (\hat{\textbf{p}}_{\tau_i}) < \textbf{b}_{j, \textrm{max}} \\ 0 & \quad \textrm{otherwise} \end{cases} \end{equation}\]

최종 할당은 다음과 같다.

\[\begin{equation} \textbf{B} (\tau_i, \textbf{G}_{\textbf{K}_j}) = \textbf{B}_1 (\tau_i, \textbf{G}_{\textbf{K}_j}) + \textbf{B}_2 (\tau_i, \textbf{G}_{\textbf{K}_j}) \end{equation}\]

위의 전략을 적용했음에도 불구하고 매우 고르지 않은 분포나 빈 block이 여전히 존재할 수 있다. Overfitting을 방지하기 위해 $K_j$가 특정 threshold를 초과할 때까지 경계 \(\textbf{b}_{j, \textrm{min}}\)과 \(\textbf{b}_{j, \textrm{max}}\)를 확대한다. 이 프로세스는 각 block에 대한 충분한 학습 데이터를 보장하기 위해 데이터 할당에만 사용된다.

Fine-tuning과 후처리

데이터와 primitive 분할 후, 각 block을 병렬로 학습시킨다. 이 fine-tuning 단계는 원래의 축소되지 않은 공간에서 진행된다. 먼저, global Gaussian prior를 활용하여 각 block을 초기화한다. 학습 loss는 L1 loss와 SSIM loss의 가중 합으로 구성된 원래 3DGS의 loss를 사용한다. 그런 다음 각 block에 대해 공간 경계 내에 포함된 fine-tuning된 Gaussian을 필터링한다. Global Gaussian prior 덕분에 block 간의 간섭이 상당히 완화되며, 직접적인 concatenation을 통해 고품질의 전체 모델을 얻을 수 있다.

2. Level-of-Detail (LoD)

불필요한 Gaussian이 rasterizer에 가져오는 계산 부담을 제거하기 위해, CityGS는 여러 LoD를 생성하고 block별로 보이는 Gaussian을 선택한다.

LoD 생성

물체가 카메라에서 멀어질수록 화면에서 차지하는 영역이 줄어들고 디테일도 줄어든다. 따라서 멀리 떨어진 LoD가 낮은 영역은 용량이 적은 모델, 즉 포인트가 적고 feature 차원이 적으며 데이터 정밀도가 낮은 모델로 잘 표현할 수 있다. 실제로 학습된 Gaussian에서 직접 작동하는 LightGaussian을 사용하여 다양한 LoD를 생성하여 성능 저하를 최소화하면서 상당한 압축률을 달성한다. 결과적으로 필요한 Gaussian에 대한 메모리 및 계산량이 상당히 완화되고 렌더링 품질은 여전히 잘 유지된다.

LoD 선택과 융합

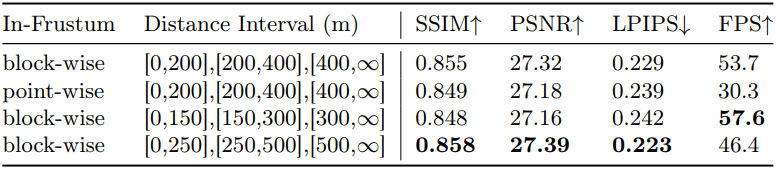
단순한 LoD 선택 방법은 frustum 영역을 해당 LoD의 Gaussian으로 채우는 것이다. 그러나 이 방법은 포인트당 거리 계산 및 할당이 필요하여 상당한 계산 오버헤드가 발생한다. 따라서 block을 단위로 간주하는 block-wise 전략을 채택한다.

각 block은 frustum과의 교차를 계산하기 위해 꼭짓점이 8개인 정육면체로 간주된다. 특정 block에 포함된 모든 Gaussian은 동일한 LoD를 공유하며, LoD는 8개의 꼭짓점에서 카메라 중심까지의 최소 거리에 의해 결정된다. 그러나 실제로 Gaussian의 최소 및 최대 좌표는 일반적으로 floater에 의해 결정되며, 이로 인해 block이 불합리하게 확대되어 많은 가짜 교차가 발생한다.

이러한 floater의 영향을 피하기 위해 Median Absolute Deviation (MAD) 알고리즘을 사용한다. $j$번째 block의 경계 \(\textbf{p}_\textrm{min}^j\)와 \(\textbf{p}_\textrm{max}^j\)는 다음과 같이 결정된다.

\[\begin{aligned} \textrm{MAD}_j &= \textrm{median} (\vert \textbf{p}_k^j - \textrm{median} (\textbf{p}_k^j) \vert) \\ \textbf{p}_\textrm{min}^j &= \max (\min (\textbf{p}_k^j), \textrm{median} (\textbf{p}_k^j) - n_\textrm{MAD} \times \textrm{MAD}_j) \\ \textbf{p}_\textrm{max}^j &= \min (\max (\textbf{p}_k^j), \textrm{median} (\textbf{p}_k^j) + n_\textrm{MAD} \times \textrm{MAD}_j) \end{aligned}\]

여기서 $n_\textrm{MAD}$는 hyperparameter이며, 적절한 $n_\textrm{MAD}$를 선택하면 block의 경계를 더 정확하게 포착할 수 있다.

그 후, 카메라 앞의 모든 꼭짓점이 screen space로 projection된다. 이러한 projection된 점들의 최소값과 최대값은 bounding box를 합성한다. Screen space에서 IoU를 계산하여 block이 frustum과 교차하는지 확인할 수 있다. 카메라가 있는 block과 함께 해당 LoD의 모든 block이 렌더링에 사용된다.

융합 단계에서는 서로 다른 LoD가 직접적인 concatenation을 통해 연결되므로 불연속성을 무시할 수 있다.

Experiments

• 데이터셋
  • 합성 장면: MatrixCity
  • 현실 장면: Residence, Sci-Art, Rubble, Building
• 구현 디테일
  • 전경: 중앙 1/3 영역
  • Global Gaussian prior 학습
    • iteration: 60,000
    • densification: 1,000 ~ 30,000 (간격: 200)
    • Building과 MatrixCity는 position과 scaling에 대한 learning rate가 3DGS의 절반
  • Fine-tuning
    • iteration: 30,000
    • learning rate
      • position: 3DGS의 40%
      • scaling: 3DGS의 80%
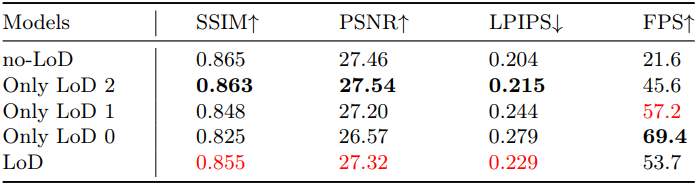
  • LoD 개수: 3
    • LoD 2: 0m ~ 200m
    • LoD 1: 200m ~ 400m
    • LoD 0: 400m ~
  • $n_\textrm{MAD}$ = 4

1. Comparison with SOTA

다음은 SOTA 방법과 성능을 비교한 표이다.

다음은 (위) 현실 장면과 (아래) MatrixCity에서 SOTA 방법과 렌더링 결과를 비교한 것이다.

2. Level of Detail

다음은 LoD의 효과를 검증한 결과이다.

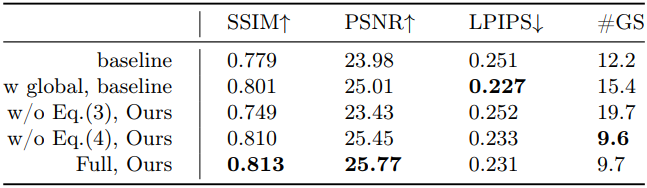
3. Ablation

다음은 학습 전략에 대한 ablation 결과이다.

다음은 LoD 전략에 대한 ablation 결과이다.