[논문리뷰] Class-Balancing Diffusion Models (CBDM)

CVPR 2023. [Paper]
Yiming Qin, Huangjie Zheng, Jiangchao Yao, Mingyuan Zhou, Ya Zhang
Cooperative Medianet Innovation Center, Shanghai Jiao-Tong University | University of Texas, Austin | Shanghai AI Laboratory
30 Apr 2023

Introduction

Diffusion model은 높은 충실도와 생성 다양성으로 알려져 있지만 대부분의 기존 diffusion model은 데이터의 레이블이 균일하게 분포된다는 가설로 학습된다. 그러나 실제 세계에서는 분포가 매우 왜곡되어 있는 경우가 많다. 각 클래스에 대해 균등하게 많은 양의 데이터를 수집하기 어렵고 학습 데이터셋의 head 카테고리는 tail 범주보다 100배 이상 다를 수 있다. 이러한 데이터셋의 경우 unconditional diffusion model은 저품질 이미지의 상당 부분을 생성하는 경향이 있다. 조건부 모델은 만족스러운 head 클래스 이미지를 생성하는 반면, tail 클래스에서 생성된 이미지는 인식할 수 없는 의미를 나타낼 가능성이 매우 높다. 제한된 데이터로 생성 모델을 학습하는 것과 관련하여 GAN 모델을 기반으로 하는 여러 방법이 이미 존재한다. 그러나 특히 diffusion model에 대한 불균형 클래스 분포의 영향을 조사하는 연구는 거의 없으며 실용적이지만 아직 탐구되지 않았다.

본 논문은 먼저 여러 long-tailed 데이터셋에 대한 불균형 생성 task에 diffusion model을 도입한 다음 long-tailed recognition에 사용되는 일반적인 방법에 따라 몇 가지 간단한 baseline을 구축한다. 왜곡된 분포로 인한 잠재적 퇴보를 극복하기 위해 새로운 Class-Balancing Diffusion Model (CBDM)을 제안한다. 이론적으로 CBDM은 생성된 이미지가 모든 샘플링 step에서 균형 잡힌 prior 분포를 갖도록 암시적으로 강제하기 위해 샘플링 동안 조건부 transfer 확률을 조정한다. 기술적으로 CBDM의 조정된 transfer 확률은 regularizer로 기능하는 조건부 diffusion model에 대해 추가적인 MSE 형태의 loss로 이어진다. 직관적으로 이 loss는 서로 다른 클래스에 따라 생성된 이미지의 유사성을 증가시키고 head 클래스에 대한 모델의 표현력을 손상시키지 않고 head 클래스에서 tail 클래스로 공통 정보를 전송하는 효과적인 접근 방식으로 밝혀졌다. CBDM은 여러 코드 라인 내에서 구현될 수 있으며 더 가벼운 버전은 기존 조건부 모델을 fine-tuning할 수 있다.

Method

1. Preliminary

Diffusion model은 은 학습에서 미리 정의된 forward process를 활용한다. 여기서 깨끗한 이미지 분포 $q(x_0)$는 timestep $t$에서 noisy한 분포 $q(x_t \vert x_0)$로 손상될 수 있다. 미리 정의된 분산 schedule \(\{\beta_t\}_{1:T}\)가 주어지면 중간 timestep에서 noisy한 분포는 다음과 같다.

\[\begin{equation} q(x_t \vert x_0) = \mathcal{N} (\sqrt{\vphantom{1} \bar{\alpha}_t} x_0, (1 - \bar{\alpha}_t) I) \\ \bar{\alpha}_t = \prod_{i=1}^t (1 - \beta_i) \end{equation}\]

이러한 forward process를 reverse시키기 위해 생성 모델 $\theta$는 다음과 같이 $x_t$에서 $x_{t-1}$을 복구하기 위해 posterior를 추정하는 방법을 학습한다.

\[\begin{equation} \min_\theta D_\textrm{KL} [q(x_{t-1} \vert x_t, x_0) \;\|\; p_\theta (x_{t-1} \vert x_t)] \end{equation}\]

이러한 목적 함수는 단순한 denoising loss로 축소될 수 있다.

\[\begin{equation} \mathcal{L}_\textrm{DDPM} = \mathbb{E}_{t, x_0 \sim q(x_0), \epsilon \sim \mathcal{N} (0,I)} [\| \epsilon - \epsilon_\theta (\sqrt{\vphantom{1} \bar{\alpha}_t} x_0 + \sqrt{1 - \bar{\alpha}_t} \epsilon, t) \|^2 ] \end{equation}\]

레이블 정보를 사용할 수 있는 경우 모델은 데이터-레이블 쌍 $(x_0, y)$가 있는 조건부 경우 $\epsilon_\theta (x_t, y, t)$와 unconditional한 경우 $\epsilon_\theta (x_t, t)$에서 위와 같이 noise를 추정하도록 학습된다. 샘플링에서 레이블 가이드 모델은 linear interpolation

\[\begin{equation} \hat{\epsilon} = (1 + \omega) \epsilon_\theta (x_t, y, t) - \omega \epsilon_\theta (x_t, t) \end{equation}\]

를 사용하여 noise를 추정하여 $x_{t−1}$을 복구한다. 이를 Classifier-Free Guidance (CFG)라고 한다.

2. Class-Balancing Diffusion Models

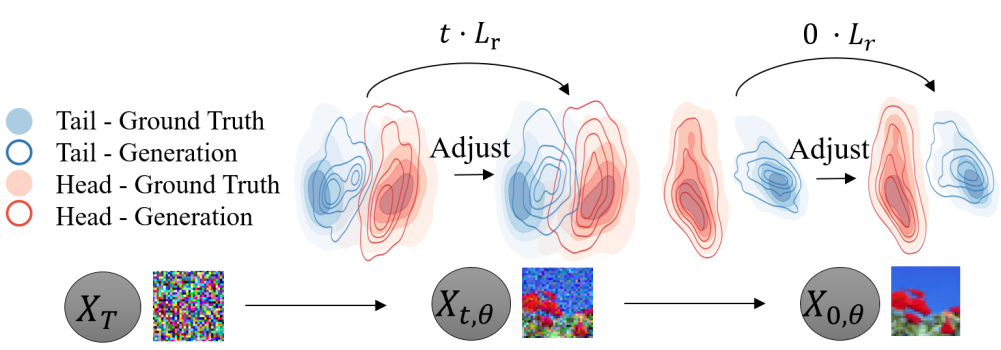
현재 diffusion model은 데이터 분포가 클래스에서 균일하다고 가정하므로 학습 단계에서 샘플을 동등하게 취급한다. 그러나 이러한 학습 전략은 생성 품질의 저하로 이어진다.

$q(x, y)$가 생성 모델에 의해 예측된 결합 분포 $p_\theta (x, y)$와 일치시켜야 하는 데이터 분포라고 가정하자. 밀도 비율

\[\begin{equation} r = \frac{q(x, y)}{p_\theta (x, y)} = \frac{q(x \vert y)}{p_\theta (x \vert y)} \cdot \frac{q(y)}{p_\theta (y)} \end{equation}\]

로부터 $q(x, y)$와 $p_\theta (x, y)$의 차이를 분석한다. 실제 레이블 분포 $q(y)$가 일반적으로 균일하다고 가정되는 prior $p_\theta (y)$와 동일할 때 밀도 비율 $r$은 조건부 모델 $p_\theta (x \vert y)$를 학습하기 위해 조건부 항으로 감소된다. 그러나 이러한 가설이 위반되면 head 클래스의 경우 $q(y) / p_\theta (y)$가 더 큰 가중치를 가져 모델이 편향되고 tail 클래스가 손상되며 그 반대의 경우도 마찬가지이다.

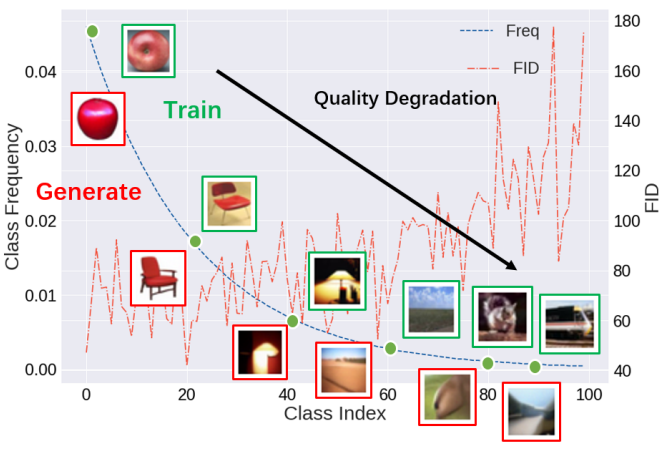
경험적으로 위 그림에 표시된 대로 tail 클래스에서 생성이 더 저하된다. 또한 head 클래스와 비교하여 DDPM은 tail 클래스 데이터 분포를 잘 캡처할 수 없으며 샘플링 프로세스 중에 mode가 제대로 다루어지지 않는다. 결과적으로 tail 클래스의 생성은 종종 품질과 다양성이 좋지 않다.

이 문제를 해결하기 위한 가장 직관적인 접근 방식은 클래스가 균형 잡힌 재샘플링을 통해 prior 레이블 분포를 조정하는 것이다. 그러나 이러한 급격한 조정은 쉽게 부정적인 개선으로 이어진다. Diffusion model의 step-by-step 샘플링 특성은 이 분포를 보다 부드럽게 조정할 수 있는 또 다른 측면을 제공한다. 클래스 분포와 prior 분포 사이에 차이가 있을 때 조건부 transition 확률 $p_\theta (x_{t−1} \vert x_t, y)$를 통해 학습 프로세스를 보정한다.

$p_\theta^\ast (x_{t−1} \vert x_t, y)$를 $q(y) / p_\theta (y)$가 올바르게 추정된 경우의 최적으로 학습된 것이라고 하고, $p_\theta (x_{t-1} \vert x_t, y)$를 클래스 불균형 케이스에서 학습된 것이라고 하자. 이러한 두 생성 분포 간의 관계는 다음과 같은 명제로 설명할 수 있다.

---

Proposition 1. 클래스 불균형 데이터셋에서 $\theta$로 parameterize된 diffusion model을 학습할 때 조건부 reverse 분포 $p_\theta (x_{t-1} \vert x_t, y)$는 조정 스키마로 다음과 같이 수정할 수 있다.

\[\begin{equation} p_\theta^\ast (x_{t-1} \vert x_t, y) = p_\theta (x_{t-1} \vert x_t, y) \frac{p_\theta (x_{t-1})}{p_\theta^\ast (x_{t-1})} \frac{q^\ast (x_t)}{q(x_t)} \end{equation}\]

---

위의 명제는 클래스 불균형 데이터셋에서 학습할 때 diffusion model이 모든 reverse step $t$에서 분포 조정 스키마를 적용하여 여전히 실제 데이터 분포에 접근할 수 있음을 보여준다. 그러나 이 스키마를 근사화하는 것은 모든 샘플링 step에서 실현 가능하지 않으므로 CBDM은 동일한 목적 함수를 달성하기 위해 학습 loss function에 이를 통합하여 model-free 부분

\[\begin{equation} \frac{q^\ast (x_t)}{q(x_t)} \end{equation}\]

를 제거한다. $p_\theta (x_{t−1})$와 $p_\theta^\ast (x_{t−1})$을 조건부 확률 $p_\theta^\ast (x_{t−1} \vert x_{t:T}, y)$의 기대값으로 더 분해하여 이 확률을 근사화하기 위한 상한을 Proposition 2에서 제시한다.

---

Proposition 2. 조정된 loss

\[\begin{equation} \mathcal{L}_\textrm{DM}^\ast = \sum_{t=1}^T \mathcal{L}_{t-1}^\ast \end{equation}\]

의 경우 timestep $t$에서 보정할 학습 목적 함수의 상한은 다음과 같이 도출할 수 있다.

\[\begin{aligned} \sum_{t \ge 1} \mathcal{L}_{t-1}^\ast =\;& \sum_{t \ge 1} D_\textrm{KL} [q(x_{t-1} \vert x_t, x_0) \;\|\; p_\theta^\ast (x_{t-1} \vert x_t, y)] \\ =\;& \sum_{t \ge 1} ( \underbrace{D_\textrm{KL} [q(x_{t-1} \vert x_t, x_0) \;\|\; p_\theta (x_{t-1} \vert x_t, y)]}_{\textrm{Diffusion model loss } \mathcal{L}_\textrm{DM}} \\ &+ \underbrace{ t \mathbb{E}_{y' \sim q_{\mathcal{Y}}^\ast } [ D_\textrm{KL} [ p_\theta (x_{t-1} \vert x_t) \;\|\; p_\theta (x_{t-1} \vert x_t, y') ]] }_{\textrm{Distribution adjustment loss } \mathcal{L}_r} ) \end{aligned}\]

---

위 명제의 상한은 두 부분으로 간주할 수 있다. 첫 번째 항 \(\mathcal{L}_\textrm{DM}\)은 일반 DDPM loss에 해당한다. 두 번째 loss \(\mathcal{L}_r\)은 정규화 항을로 분포를 조정하는 데 사용된다. 대략적으로 말하면 \(\mathcal{L}_r\)은 모델의 출력과 임의의 타겟 클래스 간의 유사성을 높인다. 따라서 head 클래스에 대한 overfitting의 위험을 줄이고 다른 클래스에서 얻은 지식을 통해 tail 클래스에 대한 생성 다양성을 확대한다. \(q_\mathcal{Y}^\ast\)가 데이터셋보다 tail이 짧을 때, 이 loss는 또한 학습 중에 선택될 과소 표현된 tail 샘플의 확률을 증가시킨다.

3. Training algorithm

CBDM의 상세한 학습 알고리즘은 Algorithm 1과 같다.

알고리즘에서 분포 조정 loss \(\mathcal{L}_r\)을 Monte-Carlo 샘플을 사용하여 MSE로 줄인다. 여기서 $\mathcal{Y}$는 분포 \(q_\mathcal{Y}^\ast\)를 따르는 샘플 세트이고 $y$는 이미지 레이블을 나타낸다. CFG의 경우 조건을 삭제할 고정 확률 (보통 10%)이 있다 (즉, $y$ = None).

\[\begin{equation} \mathcal{L}_r (x_t, y, t) = \frac{1}{| \mathcal{Y} |} \sum_{y' \in \mathcal{Y}} [t \| \epsilon_\theta (x_t, y) - \epsilon_\theta (x_t, y') \|^2 ] \end{equation}\]

CBDM은 모델 아키텍처를 채택하고 학습 loss \(\mathcal{L}_\textrm{DM}\)을 조정하여 임의의 기존 조건부 diffusion model에 적용시킬 수 있다. 특히 정규화 가중치 $\tau$의 선택은 밀도 비율

\[\begin{equation} \frac{p_\theta (x_t)}{p_\theta^\ast (x_t)} \end{equation}\]

의 선명도에 영향을 미친다. 또한 샘플링 세트 $\mathcal{Y}$의 선택은 CBDM의 또 다른 중요한 관점이며, 조정하려는 대상 분포에 따라 달라진다. 일반성을 잃지 않고 두 가지 경우에 대해 논의한다.

1. 레이블 분포를 클래스 균형 레이블 분포로 조정할 수 있다. 여기에서 레이블을 샘플링하여 \(\mathcal{Y}^\textrm{bal}\)을 구성한다.
2. 데이터 분포가 heavily longtailed인 경우, 안정된 학습을 위해 조정된 분포를 상대적으로 클래스 불균형이 적은 분포로 타겟팅할 수도 있다.

CBDM은 여러 메커니즘에서 두 경우 모두 잘 작동할 수 있다.

또한 이 loss로 naive하게 최적화하면 모델이 조건 $y$에 관계없이 동일한 결과를 출력하여 조건부 생성 성능을 저하시키는 일부 자명한 해로 모델이 붕괴될 수 있다. 따라서 이 문제를 방지하기 위해 stop-gradient 연산을 적용한다. CBDM의 최종 loss는 다음과 같다.

\[\begin{aligned} \mathcal{L}_\textrm{CBDM}^{\tau, \gamma, \mathcal{Y}} (x_t, y, t, \epsilon) &= \| \epsilon_\theta (x_t, y) - \epsilon \|^2 \\ &+ \frac{\tau t}{| \mathcal{Y} |} \sum_{y' \in \mathcal{Y}} (\| \epsilon_\theta (x_t, y) - \textrm{sg} (\epsilon_\theta (x_t, y')) \|^2 \\ &\quad \qquad \qquad + \gamma \| \textrm{sg} (\epsilon_\theta (x_t, y)) - \epsilon_\theta (x_t, y') \|^2 ) \end{aligned}\]

여기서 $\textrm{sg}(\cdot)$는 stop-gradient 연산을 나타낸다. $\tau$와 $\gamma$는 각각 정규화 항과 commitment 항의 가중치이며, 기본 설정에서 $\gamma = 1/4$로 설정된다. $\vert \mathcal{Y} \vert$은 레이블 세트의 element 수를 나타낸다.

Experimental results

• 데이터셋: CIFAR10LT, CIFAR100LT ($imb = 0.01$)
• 구현 디테일
  • DDPM: $\beta_1 = 10^{-4}$, $\beta_T = 0.02$, $T = 1000$
  • Optimizer: Adam
  • Leraning rate: $2 \times 10^{-4}$ (warmup 5000 epochs)

1. Main results

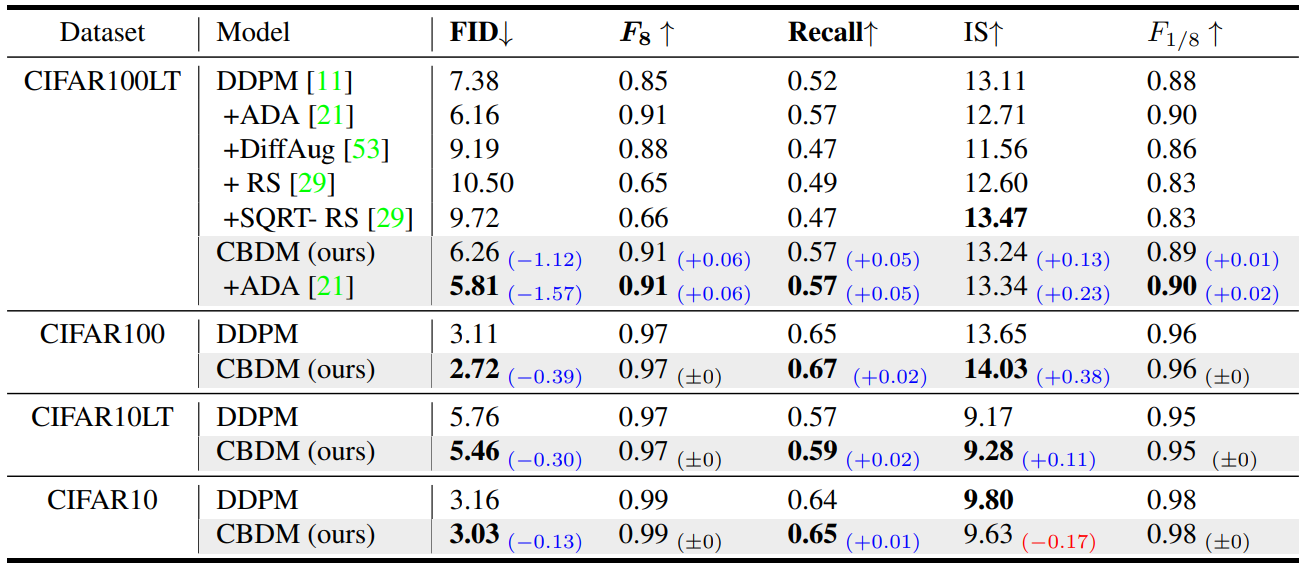
다음은 다양한 데이터셋에서의 CBDM의 성능이다.

다음은 heavily tail-distributed 클래스와 mild tail-distributed 클래스에 대한 생성 결과를 DDPM과 비교한 것이다.

Case-by-case study

다음은 클래스별 FID를 DDPM과 비교한 그래프이다.

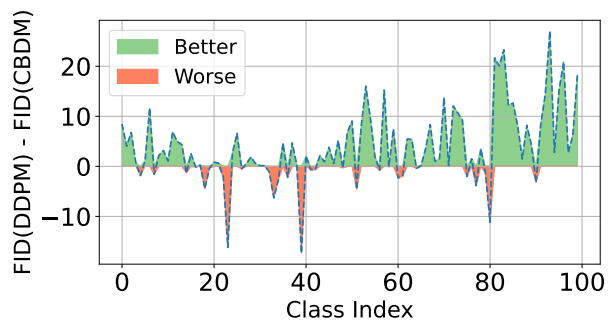
The choice of label set $\mathcal{Y}$

다음은 다양한 정규화 샘플링 세트 $\mathcal{Y}$에 대한 성능을 비교한 표이다.

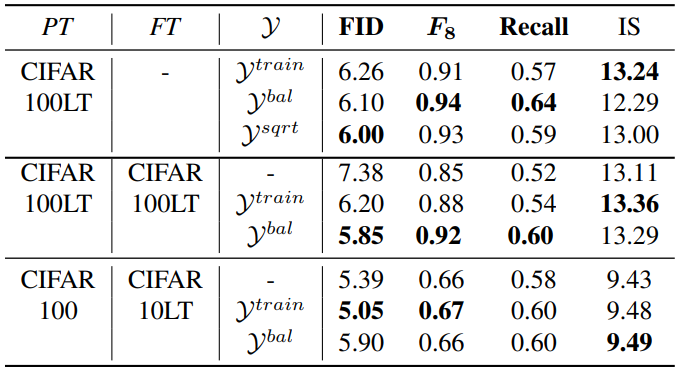
Enhancement of training classifiers on long-tailed data

다음은 다양한 학습 데이터에 대한 recognition 결과이다.

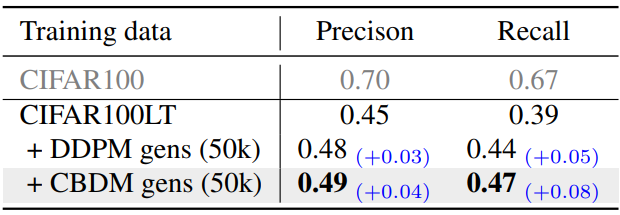
Comparison with other benchmarks

다음은 CIFAR에서 long-tailed SOTA들과 비교한 표이다.

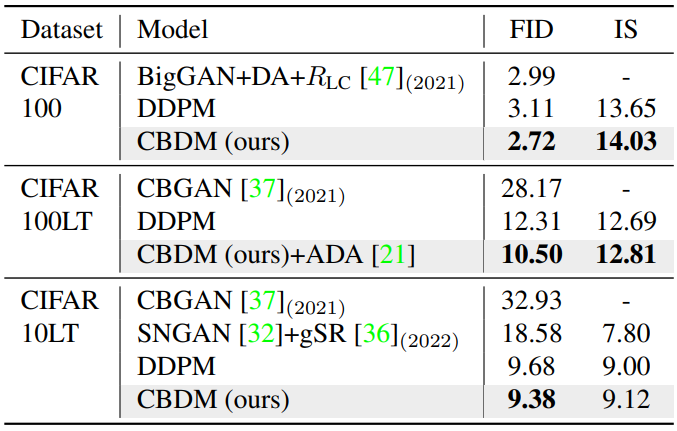
3. Ablations

Compatibility with different backbones

다음은 CIFAR100LT 데이터셋에서 다양한 backbone을 사용할 때의 결과를 비교한 표이다.

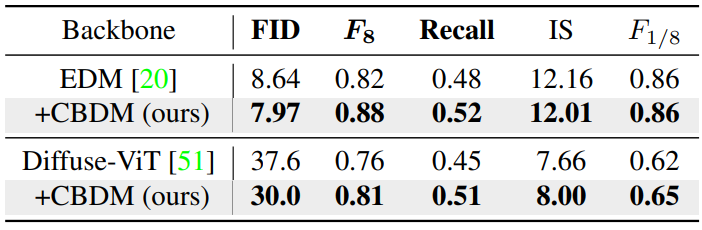
CBDM with DDIM sampling

다음은 100 DDIM step으로 샘플링한 결과이다.

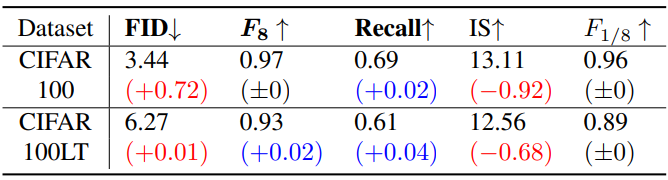
Effects of hyperparameters

다음은 다양한 정규화 가중치 $\tau$에 대한 이미지 품질이다.

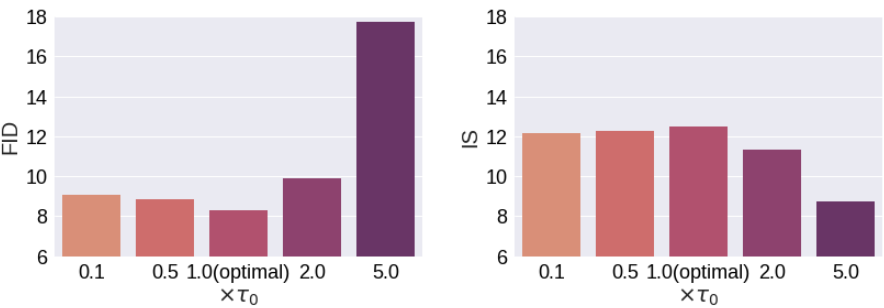
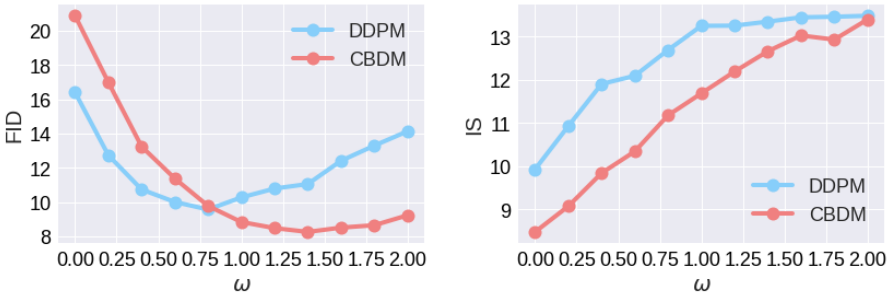
Guidance strength $\omega$

다음은 다양한 guidance 강도 $\omega$에 대한 이미지 품질이다.

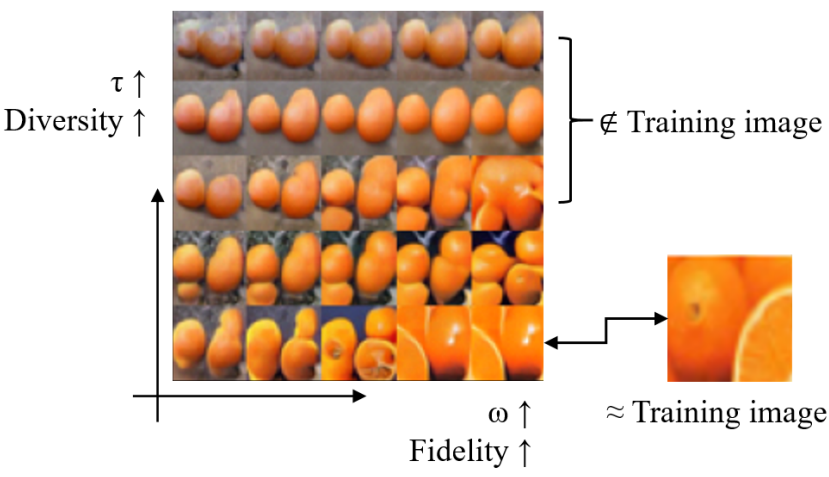
Fidelity-diversity control

다음은 guidance 강도 $\omega$와 정규화 가중치 $\tau$에 의해 이미지의 충실도와 다양성을 제어한 결과이다.