[논문리뷰] CARD: Classification and Regression Diffusion Models
NeurIPS 2022. [Paper]
Xizewen Han, Huangjie Zheng, Mingyuan Zhou
Department of Statistics and Data Sciences, The University of Texas at Austin
15 Jun 2022
Introduction
통계 및 기계 학습의 기본 문제는 일련의 공변량 $x$가 주어지면 응답 변수 $y$를 예측하는 것이다. 일반적으로 $y$는 regression에서는 연속 변수이고 classification에서는 카테고리형 변수이다. $x$를 $C$ 차원 출력으로 변환하는 deterministic function을 $f(x) \in \mathbb{R}^C$로 나타낸다. $f(x)$의 $c$번째 차원을 $f_c(x)$로 나타낸다. 기존 방법은 일반적으로 additive noise model을 가정한다. $y \in \mathbb{R}^C$를 사용하는 regression의 경우
\[\begin{equation} y = f(x) + \epsilon, \quad \epsilon ∼ \mathcal{N}(0, \Sigma) \end{equation}\]을 가정하고, 반면 \(y \in \{1, \cdots, C\}\)의 classification의 경우
\[\begin{equation} y = \arg \max (f_1(x) + \epsilon_1, \cdots, f_C (x) + \epsilon_C), \quad \epsilon_c \sim \textrm{EV}_1 (0, 1) \end{equation}\]이다. 여기서 $\textrm{EV}_1 (0, 1)$은 standard type-1 extreme value distribution이다. 따라서 주어진 $x$에 대한 $y$의 기대값은 regression의 경우
\[\begin{equation} \mathbb{E} [y \vert x] = f(x) \end{equation}\]이고 classification의 경우
\[\begin{equation} P(y = c \vert x) = \mathbb{E}[y = c \vert x] = \textrm{softmax}_c (f(x)) = \frac{\exp(f_c (x))}{\sum_{c'=1}^C \exp(f_{c'} (x))} \end{equation}\]이다.
이러한 additive noise model은 주로 조건부 평균 $\mathbb{E}[y \vert x]$를 정확하게 추정하는 데 초점을 맞추는 반면 noise 분포가 주어진 $x$에 대한 $y$의 불확실성을 정확하게 캡처할 수 있는지 여부에는 주의를 덜 기울인다. 이러한 이유로 주어진 $x$에 대한 $y$의 분포가 additive-noise 가정에서 분명히 벗어나는 경우 제대로 작동하지 않을 수 있다. 예를 들어, $p(y \vert x)$가 multimodal인 경우 ($x$에 누락된 카테고리형 공변량이 있을 때 일반적으로 발생) $\mathbb{E}[y \vert x]$는 주어진 특징 $x$에 대한 $y$의 어떠한 가능한 참 값에도 가깝지 않을 수 있다.
보다 구체적으로, 체중, 키, 혈압, 나이는 알려져 있지만 성별이 알려지지 않은 사람을 고려하면 이 사람의 테스토스테론 수치나 에스트로겐 수치는 쌍봉(bi-modal) 분포를 따를 가능성이 높으며 유방암 발병 가능성도 쌍봉 분포를 따를 가능성이 높다. 따라서 $y$의 조건부 평균을 특성화하기 위해 deterministic function $f(x)$를 사용하는 이러한 널리 사용되는 additive noise model은 본질적으로 불확실성 추정 능력이 제한적이다.’
본 논문의 목표는 주어진 $N$개의 학습 데이터 포인트 셋 \(\mathcal{D} = \{(x_i, y_i)\}_{1,N}\)에 대하여 $x$로 컨디셔닝된 $y$의 전체 분포를 정확하게 복구하는 것이다. 이 목표를 실현하기 위해 diffusion 기반 (일명 score 기반) 생성 모델을 고려한다. Forward 및 reverse diffusion chain 모두에 공변량 의존성을 주입한다. 본 논문의 방법은 연속형 및 카테고리형 $y$ 변수 모두의 조건부 분포를 모델링할 수 있으며 이 방법으로 개발된 알고리즘을 총칭하여 Classification And Regression Diffusion (CARD) model이라고 한다.
Diffusion 기반 생성 모델은 고해상도 실사 이미지와 같은 고차원 데이터를 생성하는 능력뿐만 아니라 학습 안정성으로 인해 최근 상당한 주목을 받고 있으며, score matching과 Langevin dynamics의 관점에서 이해할 수 있다. 또한 diffusion probabilistic model의 관점에서 이해할 수 있는데, 먼저 forward diffusion을 정의하여 데이터를 noise로 변환한 다음 reverse diffusion을 정의하여 noise에서 데이터를 재생성한다.
이러한 이전 방법들은 주로 unconditional한 생성 모델링에 중점을 둔다. 레이블, 텍스트 또는 손상된 이미지의 의미론적 의미 또는 컨텐츠와 일치하는 고해상도 실사 이미지를 생성하는 것을 목표로 하는 guided-diffusion model이 존재하지만, 본 논문은 보다 근본적인 diffusion 기반 조건부 생성 모델링을 연구하는 데 중점을 둔다. 특히, CARD가 데이터 \(\mathcal{D} = \{(x_i, y_i)\}_{1,N}\)을 관찰한 후 $p(y \vert x, \mathcal{D})$를 정확하게 복구하는 데 도움이 될 수 있는지 철저히 조사하는 것이다. 즉, 해당 공변량이 주어진 연속적인 또는 카테고리 응답 변수의 회귀 분석에 중점을 둔다.
Methods and Algorithms for CARD
Ground-truth 응답 변수 $y_0$와 그 공변량 $x$가 주어지고 diffusion model에 의해 만들어진 일련의 중간 예측 $y_{1:T}$를 가정하면 지도 학습의 목표는 다음과 같은 ELBO를 최적화하여 log-likelihood가 최대화되도록 모델을 학습하는 것이다.
\[\begin{equation} \log p_\theta (y_0, x) = \log \int p_\theta (y_{0:T} \vert x) dy_{1:T} \ge \mathbb{E}_{q(y_{1:T} \vert y_0, x)} \bigg[ \log \frac{p_\theta (y_{0:T} \vert x)}{q (y_{1:T} \vert y_0, x)} \bigg] \end{equation}\]$q (y_{1:T} \vert y_0, x)$는 diffusion model에서 forward process 또는 diffusion process이라 불린다. 위의 목적 함수는 다음과 같이 다시 쓸 수 있다.
\[\begin{aligned} \mathcal{L}_\textrm{ELBO} (y_0, x) &:= \mathcal{L}_0 (y_0, x) + \sum_{t=2}^T \mathcal{L}_{t-1} (y_0, x) + \mathcal{L}_T (y_0, x) \\ \mathcal{L}_0 &:= \mathbb{E}_q [- \log p_\theta (y_0 \vert y_1, x)] \\ \mathcal{L}_{t-1} &:= \mathbb{E}_q [D_\textrm{KL} (q(y_{t-1} \vert y_t, y_0, x) \; \| \; p_\theta (y_{t-1} \vert y_t, x))] \\ \mathcal{L}_T (y_0, x) &:= \mathbb{E}_q [D_\textrm{KL} (q(y_T \vert y_0, x) \; \| \; p (y_T \vert x))] \end{aligned}\]여기서 \(\mathcal{L}_T\)가 어떤 파라미터에도 의존하지 않고 미리 가정된 분포 $p(y_T \vert x)$ 쪽으로 관찰된 응답 변수 $y_0$를 조심스럽게 diffuse함으로써 0에 가깝다고 가정하는 관례를 따른다. 나머지 항은 모델 $p_\theta (y_{t−1} \vert y_t, x)$를 모든 timestep에 대해 tractable한 ground-truth denoising transition step $q(y_{t−1} \vert y_t, y_0, x)$에 근사하게 만든다. Vanilla diffusion model과 달리 diffusion process의 endpoint를 다음과 같이 가정한다.
\[\begin{equation} p(y_T \vert x) = \mathcal{N} (f_\phi (x), I) \end{equation}\]여기서 $f_\phi (x)$는 $x$와 $y_0$ 사이의 사전 지식이며, 예를 들어 $\mathbb{E}[y \vert x]$를 근사하도록 $\mathcal{D}$로 사전 학습된 신경망일 수도 있고, 관계를 모르는 경우 0으로 가정할 수 있다. Diffusion schedule \(\{\beta_t\}_{t = 1:T} \in (0,1)^T\)에 대하여, DiffuseVAE 논문과 비슷한 방법으로 forward process 조건부 분포를 지정하며, DiffuseVAE와 다른 점은 $t = 1$을 포함한 모든 timestep에 대하여 지정한다는 것이다.
\[\begin{equation} q(y_t \vert y_{t-1}, f_\phi (x)) = \mathcal{N} (y_t; \sqrt{1 - \beta_t} y_{t-1} + (1 - \sqrt{1 - \beta_t}) f_\phi (x), \beta_t I) \end{equation}\]위 식의 평균 항은 실제 데이터 $y_0$와 예측된 조건부 기대값 $f_\phi (x)$의 interpolation으로 볼 수 있으며, forward process에 의해 전자에서 후자로 점진적으로 변한다.
임의의 timestep에 대한 closed-form 샘플링 분포를 다음과 같다.
\[\begin{equation} q(y_t \vert y_0, f_\phi (x)) = \mathcal{N} (y_t; \sqrt{\vphantom{1} \bar{\alpha}_t} y_0 + (1- \sqrt{\vphantom{1} \bar{\alpha}_t}) f_\phi (x), (1 - \bar{\alpha}_t) I) \\ \textrm{where} \quad \alpha_t := 1 - \beta_t, \quad \bar{\alpha}_t = \prod_t \alpha_t \end{equation}\]이러한 공식은 다음과 같은 tractable한 forward process posterior에 해당한다.
\[\begin{equation} q(y_{t-1} \vert y_t, y_0, x) = q(y_{t-1} \vert y_t, y_0, f_\phi (x)) = \mathcal{N} (y_{t-1}; \tilde{\mu} (y_t, y_0, f_\phi (x)), \tilde{\beta}_t I) \end{equation}\]여기서
\[\begin{aligned} \tilde{\mu} &:= \underbrace{\frac{\beta_t \sqrt{\vphantom{1} \bar{\alpha}_{t-1}}}{1 - \bar{\alpha}_t}}_{\gamma_0} y_0 + \underbrace{\frac{(1 - \bar{\alpha}_{t-1}) \sqrt{\alpha_t}}{1 - \bar{\alpha}_t}}_{\gamma_1} y_t + \underbrace{\bigg( 1 + \frac{(\sqrt{\vphantom{1} \bar{\alpha}_t} - 1)(\sqrt{\alpha_t} + \sqrt{\vphantom{1} \bar{\alpha}_{t-1}})}{1 - \bar{\alpha}_t} \bigg)}_{\gamma_2} f_\phi (x) \\ \tilde{\beta}_t &:= \frac{1 - \bar{\alpha}_{t-1}}{1 - \bar{\alpha}_t} \beta_t \end{aligned}\]이다.
1. CARD for Regression
Regression 문제의 경우 reverse diffusion process의 목표는 관측값에 내재된 우연성 또는 로컬한 불확실성인 noise 항의 분포를 점진적으로 복구하여 샘플을 생성할 수 있도록 하는 것이며, 실제 조건부 $p(y \vert x)$와 일치하는 샘플을 생성할 수 있게 한다.
DDPM에 의해 도입된 reparmeterization에 따라 $\epsilon_\theta (x, y_t, f_\phi (x), t)$를 구성한다. $\epsilon_\theta$는 $y_t$에서 샘플링된 forward diffusion noise $\epsilon$를 예측하는 신경망으로 parameterize된 function approximator이다. 학습과 inference 절차는 표준 DDPM 방식으로 수행할 수 있다.


2. CARD for Classification
Regression과 비슷하게 classification task를 공식화할 수 있다.
- 연속적인 응답 변수를 $y_0$에 대한 one-hot label vector로 교체
- Mean approximator를 $f_\phi (x)$에 대한 클래스 레이블의 softmax 확률을 출력하는 사전 학습된 classifier로 교체
이 구성은 더 이상 $y_0$가 카테고리형 분포에서 도출된다고 가정하지 않고 대신 각 one-hot label을 클래스 프로토타입으로 취급한다. 즉, 연속 데이터와 state space를 가정하여 Gaussian diffusion model 프레임워크를 유지할 수 있다. 샘플링 절차는 probability simplex의 벡터 대신 각 차원의 실수 범위에서 재구성된 $y_0$를 출력한다. $C$를 클래스 수, $1_C$를 1의 $C$차원 벡터라고 하면, 이러한 출력을 temperature-weighted Brier score의 softmax 형식의 확률 벡터로 변환하여 예측과 $1_C$ 사이의 제곱 오차를 계산한다. 수학적으로 $k$번째 클래스를 예측할 확률과 최종 포인트 예측 $\hat{y}$는 다음과 같이 표현할 수 있다.
\[\begin{equation} \textrm{Pr} (y = k) = \frac{\exp(-(y_0 - 1_C)_k^2 / \tau)}{\sum_{i=1}^C \exp(-(y_0 - 1_C)_i^2 / \tau)} \\ \hat{y} = \underset{k}{\arg \max} (-(y_0 - 1_C)_k^2) \end{equation}\]여기서 $\tau > 0$은 temperature parameter이고, $(y_0 - 1_C)_k^2$은 $y_0$와 $1_C$ 사이의 element-wise 제곱 오차 벡터의 $k$번째 차원이다.
\[\begin{equation} (y_0 - 1_C)_k^2 = \| y_{0_k} - 1\|^2 \end{equation}\]직관적으로, 이 구성은 샘플링된 $y_0$의 출력을 가장 높은 확률로 one-hot label의 값 1로 인코딩된 실제 클래스에 가장 가까운 클래스를 할당한다.
동일한 공변량 $x$에 대한 조건부로, 생성 모델의 stochasticity는 각 reverse process 샘플링 후에 다른 클래스 프로토타입 재구성을 제공하여 모든 클래스 레이블에 대한 예측 확률 간격을 구성할 수 있게 한다. 이러한 확률적 재구성은 DALL-E 2와 유사한 방식으로 reverse diffusion process에서 텍스트 임베딩을 조건으로 이미지 임베딩을 재구성하기 전에 diffusion을 적용하며, 생성된 이미지의 다양성에 중요하다.
Experiments
1. Regression
Toy Examples
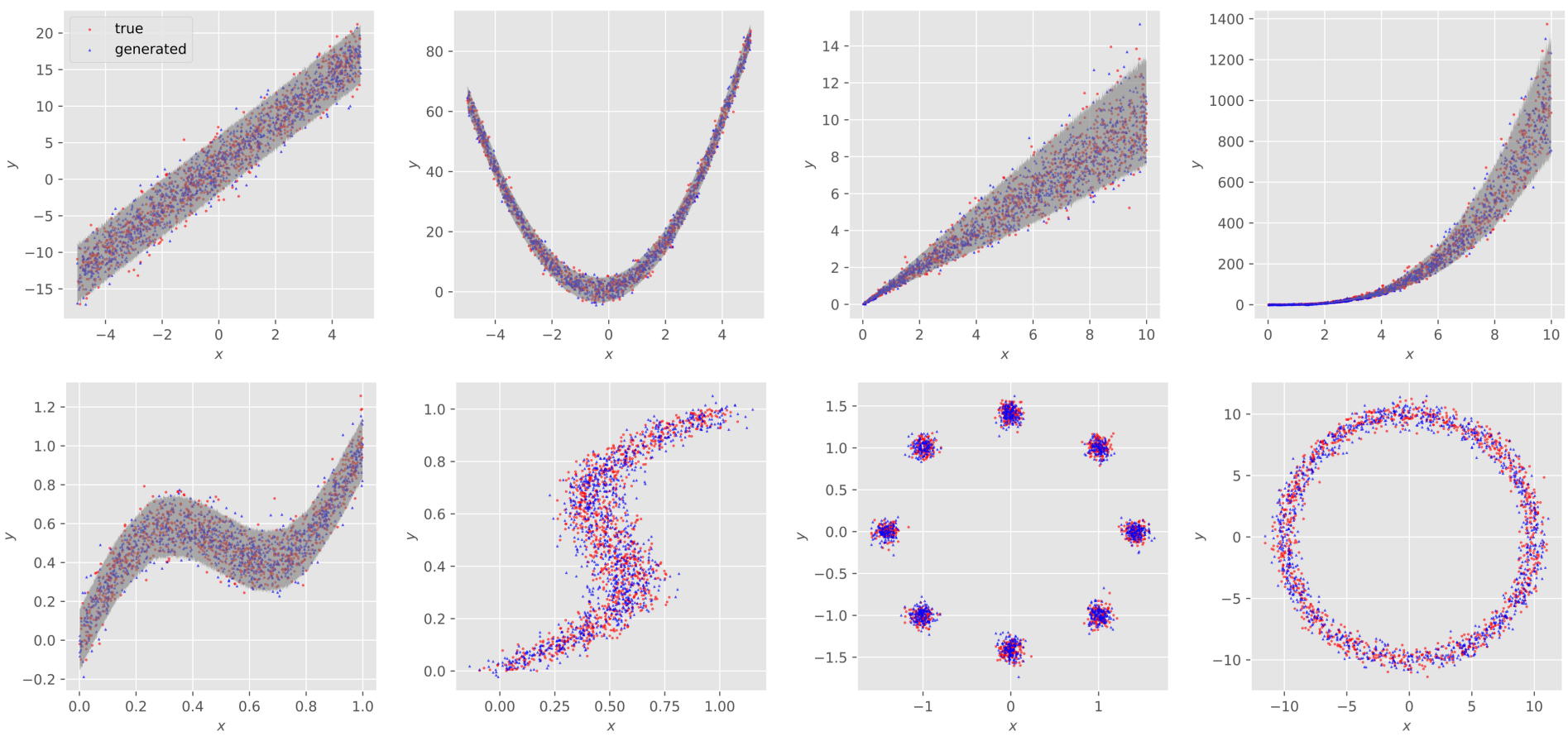
다음은 8개의 toy example에 대한 실제 데이터와 생성된 데이터의 regression을 나타낸 scatter plot이다.
UCI Regression Tasks
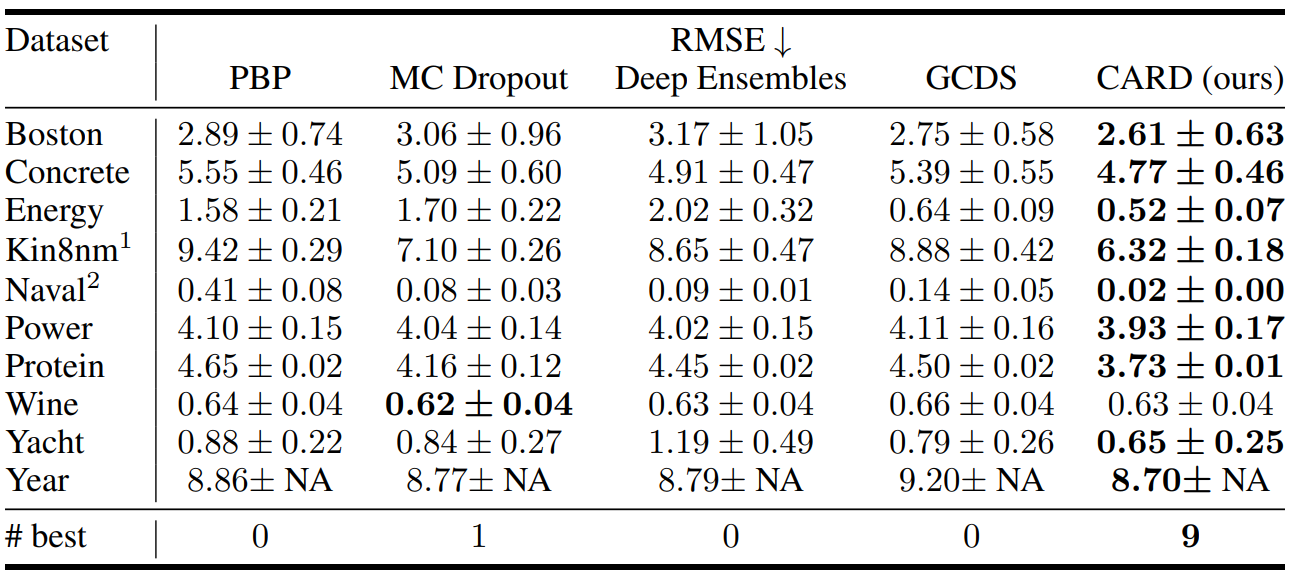
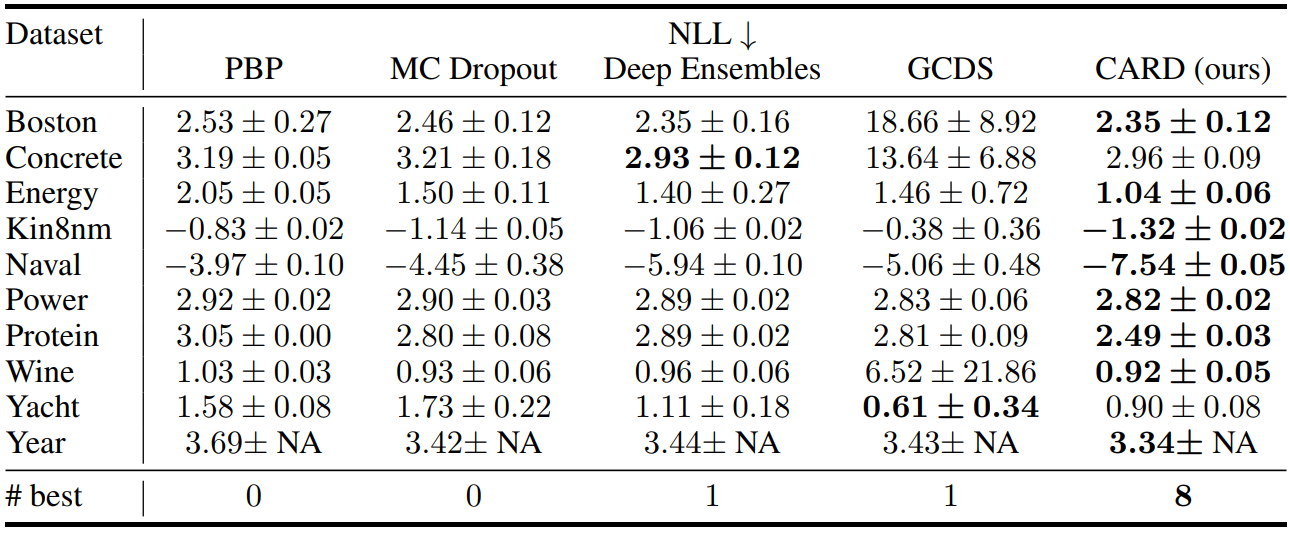
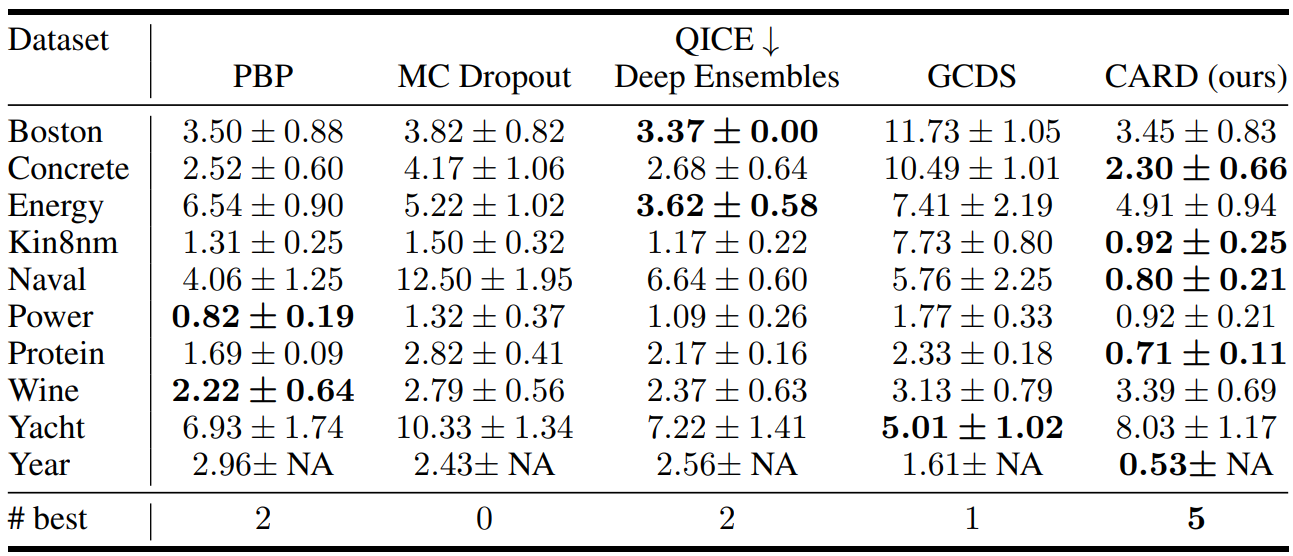
다음은 UCI regreesion task의 RMSE, NLL, QICE를 다른 모델들과 비교한 표이다.
2. Classification
Classification에 대한 저자들의 동기는 네트워크 아키텍처 설계와 밀접한 관련이 있는 벤치마크 데이터셋의 평균 정확도 측면에서 state-of-the-art 성능을 달성하는 것이 아니다. 본 논문의 목표는 두 가지다.
- 생성 모델을 통해 분류 문제를 해결하는 것을 목표로 하며 정확도 측면에서 deterministic한 출력으로 기본 classifier의 성능을 향상시키는 능력을 강조한다.
- 인스턴스 레벨에서 모델 신뢰도, 즉 생성 모델의 출력 확률을 통해 모델이 각 예측에 대해 얼마나 확실한지에 대한 아이디어를 도입하여 대안적인 불확실성을 제공한다.
CIFAR-10
다음은 CIFAR-10 classification에서의 정확도와 NLL을 다른 BNN과 비교한 표이다.

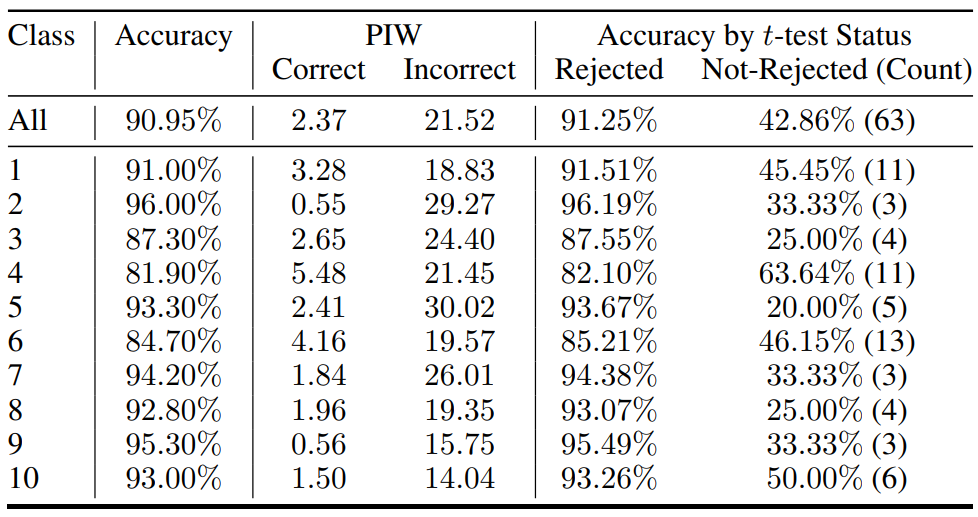
다음은 CIFAR-10 classification에서의 PIW (100배)와 $t$-test 결과이다.