[논문리뷰] Learning to Brachiate via Simplified Model Imitation
SIGGRAPH 2022. [Paper] [Page] [Github]
Daniele Reda, Hung Yu Ling, Michiel van de Panne
University of British Columbia
8 May 2022

Introduction
Brachiation은 팔만 사용하여 나뭇가지나 손잡이 사이를 이동하는 운동의 한 형태이다. Brachiating 움직임은 두 가지 유형으로 분류 될 수 있다
- Continuous contact brachiation: 항상 나무 가지와 같은 손으로 잡을 수 있는 접촉을 유지
- Ricochetal brachiation: 연속적인 grasping 사이에 비행 단계를 포함한
이 두 종류의 brachiation 중 ricochetal brachiation이 더 빠르며, 각각 걷기와 달리기와 유사하다.
심층 강화 학습(RL)은 이전에 다리, 공중 및 수중 이동에 적용되었다. 이러한 유형의 이동과 명백한 유사성에도 불구하고 brachiation은 여러면에서 독특하다. 첫째, 손잡이의 선택은 종종 불연속적이다. 이는 분명히 제어할 수 있는 feature, 즉 제어 권한이 적은 반면, 동시에 grasping에 영향을 미치기 위해 높은 공간 정밀도를 필요로 한다. 둘째, 미래의 손잡이에 도달하는 데 필요할 수 있는 모멘텀 때문에 일련의 손잡이에 걸친 동작의 사전 계획이 더 중요해진다. 마지막으로, brachiation은 매우 효율적인 수평 운동의 가능성을 제공한다. 이상적인 점 질량은 에너지 손실 없이 번갈아 진자 모양의 스윙과 포물선 비행 단계를 따를 수 있다.
본 논문에서는 14-link의 평면 다관절 모델을 시뮬레이션하기 위해 완전히 학습된 솔루션을 제시한다. Brachiation에 대한 이전 연구들과 유사하게 모델은 고정된 부착 모델을 grasping 역학의 proxy로 사용한다.
Environments
1. Simplified Model
본 논문의 단순화된 모델은 긴팔원숭이를 가상의 확장 가능한 팔이 장착된 점 덩어리로 취급한다. 가상 팔은 $r_\textrm{min}$ = 10cm이고 $r_\textrm{max}$ = 75cm인 반경 $r \in [r_\textrm{min}, r_\textrm{max}]$로 정의된 환형 영역 (두 동심원 사이의 영역) 내에서 손으로 잡을 수 있다. $r_\textrm{max}$는 전체 모델의 팔 길이(60cm)보다 크지만 단순화된 모델은 어깨가 아닌 긴팔원숭이의 질량 중심을 대신하도록 의도되었다.
단순화된 모델 동역학은 두 개의 교대 단계로 구성된다. 스윙 단계는 손 중 하나가 타겟 손잡이에(또는 근처에) 있을 때 캐릭터가 잡기를 수행할 때 시작된다. 이 단계에서 캐릭터는 잡는 팔의 방향을 따라 힘을 가하여 현재 손잡이 쪽으로 당기거나 밀어낼 수 있다. 스윙 단계 동역학은 스프링-댐퍼 점-질량 진자 시스템과 동일하다. 캐릭터는 진자의 스윙 암을 줄이거나 늘려 각속도에 영향을 줄 수 있다.
비행 단계는 어느 손도 잡지 않는 기간으로 정의된다. 이 단계에서 캐릭터의 궤적은 포물선 궤적을 따라 수동 물리학의 지배를 받는다. 비행 단계 동안 유지되는 control 권한은 도달 거리 내에 있는 경우 다음 손잡이를 언제 잡을지 결정하는 데서 온다.
최소 및 최대 팔 길이는 스윙 단계 동안 길이 제한이 위반될 때 충격량을 적용한다. 저자들은 GPU에서 간단하게 병렬화할 수 있는 PyTorch에서 단순화된 환경의 물리 시뮬레이션을 구현하였다.
2. Full Model
전체 모델은 실제 긴팔원숭이의 형태에 근접한 긴팔원숭이 같은 캐릭터의 평면 관절 모델이며 PyBullet을 사용하여 시뮬레이션된다.
긴팔원숭이 모델은 어깨, 팔꿈치, 손목, 엉덩이, 무릎, 발목을 포함한 13개의 경첩 관절과 골반의 단일 허리 관절로 구성된다. 수동적이라고 생각하는 손목 관절을 제외한 모든 관절에는 연관된 토크가 있다. Ball-and-socket 관절의 3D 동작을 2차원으로 캡처하기 위해 어깨 관절을 해당 관절 제한 없이 경첩 관절로 모델링한다. 이렇게 하면 시뮬레이션된 캐릭터가 실제 긴팔원숭이의 언더스윙 동작을 생성할 수 있다. 이 긴팔원숭이의 총 질량은 9.8kg, 팔 길이는 60cm, 서 있는 높이는 63cm이다. 시뮬레이션 안정성을 향상시키기 위해 손과 발의 질량을 인위적으로 늘린다. 긴팔 원숭이 모델의 물리적 특성은 아래 표에 요약되어 있다.
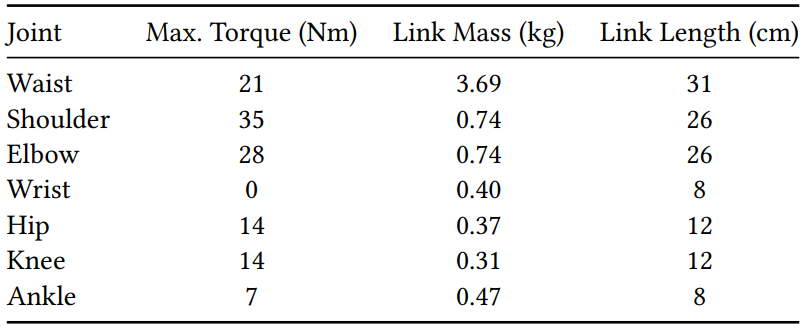
전체 모델의 잡기 동작은 지점 간 제약 조건을 사용하여 시뮬레이션된다. 이를 통해 손-물체 동역학 모델링의 복잡성을 추상화할 수 있지만 여전히 기본 물리학에 대한 합리적인 근사치를 제공한다. 저자들의 구현에서는 캐릭터가 잡기를 수행하고 손이 타겟 손잡이에서 5cm 이내에 있을 때 지점 간 제약 조건이 생성된다. 제약 조건은 바람직하지 않은 가상의 힘이 도입되는 것을 방지하기 위해 타겟 손잡이 위치와 반대로 잡는 손을 현재 위치에 고정한다. 해제 시 제약 조건이 제거된다.
3. Handhold Sequences Generation
단순화된 캐릭터와 전체 캐릭터는 모두 동일한 환경에서 작동하며 여기에는 손집이 시퀀스가 포함된다. Brachiation task에서 목표는 연속적인 손잡이를 정확하게 잡고 앞으로 나아가는 것이다. 연속적인 손잡이는 이전 손잡이에 상대적인 거리 $d \sim \mathcal{U} (1, 2)$ 미터와 피치 $\phi \sim [-15^\circ, 15^\circ]$로 정의된 균일한 분포로부터 생성된다.
4. Action Spaces
단순화된 모델과 전체 모델은 모두 60Hz의 control 주파수를 사용하고 시뮬레이션 주파수는 480Hz이다.
단순화된 모델의 action space는 타겟 길이 offset과 잡기 또는 놓기를 나타내는 flag의 두 가지 값으로 구성된다. 각 control 단계를 시작할 때 타겟 길이 offset이 현재 팔 길이에 추가되어 원하는 타겟 길이를 형성한다. 또한 grab flag는 현재 캐릭터 상태를 결정하는 데 사용된다. 각 시뮬레이션 단계에서 적용되는 힘은 원하는 타겟 길이를 기준으로 PD 제어를 사용하여 계산된다. 최대 가해지는 힘은 실제 긴팔원숭이의 최대 힘과 가까운 240N으로 고정된다.
전체 모델에서 action space는 단순화된 모델의 action space와 유사하며 모든 관절에만 확장된다. ACtion은 13개의 관절 각각에 대한 관절 각도 offset을 나타내는 15개의 파라미터와 각 손에 대한 잡기 또는 해제를 나타내는 flag로 구성된다. 각 관절에 적용된 토크는 PD 제어를 사용하여 계산된다. 각 관절에 대한 proportional gain $k_p$를 라디안 단위의 action 범위와 동일하게 설정하고 derivative gain을 $k_p / 10$으로 설정한다.
5. State Spaces
두 환경 모두 유사한 state space를 가지며, 캐릭터 정보와 향후 잡을 손잡이 시퀀스에 대한 정보로 구성된다.
단순화된 환경에서 캐릭터 state는 월드 좌표의 루트 속도와 현재 스윙 단계 시작 이후 경과 시간으로 구성된 3차원이다. 경과 시간 정보는 환경이 최소 및 최대 잡기 시간을 적용하기 때문에 환경을 완전히 관찰할 수 있도록 만드는 데 필요하다. 경과 시간을 최대 허용 잡기 시간으로 나누어 정규화한다. 0은 캐릭터가 잡고 있지 않음을 나타내고 1은 최대 시간 동안 잡았음을 나타낸다.
전체 모델의 캐릭터 state는 루트 속도, 루트 피치, 조인트 각도, 조인트 속도, 잡기 팔 높이, 잡기 상태로 구성된 45 차원 벡터이다. 몸통은 루트 링크로 사용된다. 루트 속도($\mathbb{R}^2$)는 시상면(sagittal plane)에서의 속도이다. 관절 각도($\mathbb{R}^{26}$)는 각 관절의 $\cos(\theta)$와 $\sin(\theta)$로 표현되며, 여기서 $\theta$는 현재 각도이다. 관절 속도($\mathbb{R}^{13}$)는 초당 라디안으로 측정된 각속도이다. 그랩 팔 높이($\mathbb{R}$)는 자유로운 손과 위쪽 방향의 루트 사이의 거리로, 다음 목표에 도달할 수 있는지 여부를 유추하는 데 사용할 수 있다. 마지막으로, 잡기 상태($\mathbb{R}^2$)는 각 손이 현재 잡고 있는지를 나타내는 bool flag이다.
두 환경 모두에서 control policy는 캐릭터 state 외에 손으로 잡을 위치와 관련된 task 정보를 받는다. 특히 task 정보에는 캐릭터의 좌표계에서 현재 손잡이 위치와 다가올 손잡이 위치 $N$개가 포함된다.
Learning Control Policies
심층 강화 학습 (DRL)을 사용하여 단순화된 환경과 세부적인 환경 모두에서 brachiation 기술을 학습시킨다. RL에서 각 timestep $t$에서 control policy는 action $a_t$을 수행하여 환경 state $s_t$에 반응한다. 수행된 action에 따라 policy는 reward 신호 $r_t = r (s_t, a_t)$를 피드백으로 받는다. DRL에서 policy는 신경망 $\pi_\theta (a \vert s)$를 사용하여 $a_t$를 계산한다. 여기서 $\pi_\theta (a \vert \cdot)$는 현재 policy에서 $a$의 확률 밀도이다. DRL의 목표는 다음을 최대화하는 네트워크 파라미터 $\theta$를 찾는 것이다.
\[\begin{equation} J_\textrm{RL} (\theta) = \mathbb{E} \bigg[ \sum_{t=0}^\infty \gamma^t r (s_t, a_t) \bigg] \end{equation}\]여기서 $\gamma \in [0, 1)$는 합이 수렴하도록 하는 discount factor이다. Policy gradient actor-critic 알고리즘인 Proximal Policy Optimization (PPO) 알고리즘을 사용하여 이 최적화 문제를 해결한다. 저자들은 병렬 세팅에서 하드웨어 리소스를 효과적으로 활용하여 학습 시간을 줄이기 위해 PPO를 선택하였다. 학습 파이프라인은 공개적으로 사용 가능한 PPO 구현을 기반으로 한다.
1. System Overview
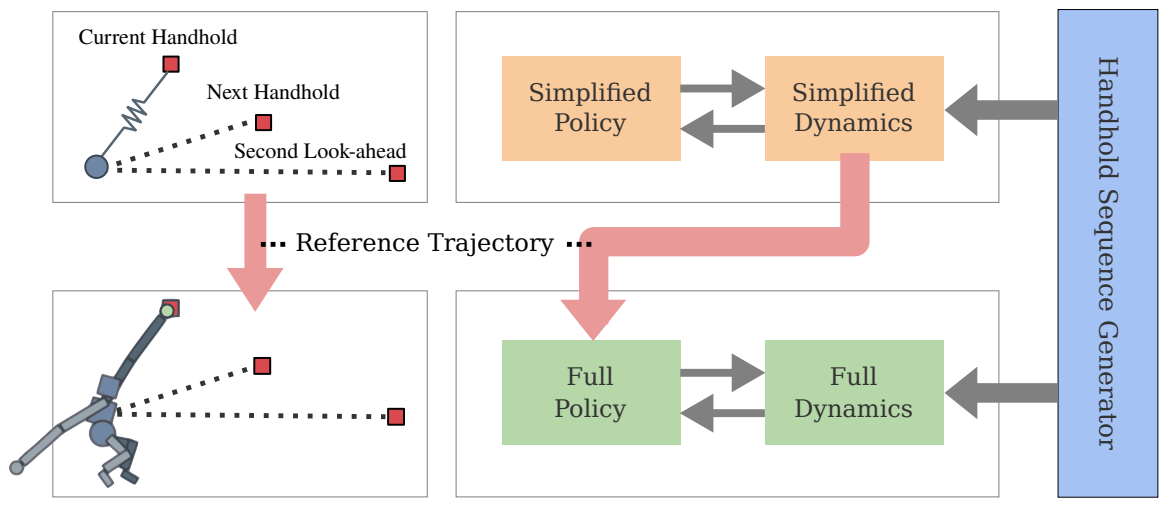
시스템 개요는 위 그림과 같다. 시스템에는 단순화된 모델, 전체 모델, 손잡이 시퀀스 생성기의 세 가지 구성 요소가 포함되어 있다. 학습 중에 단순화된 모델은 먼저 손잡기 생성기에 의해 생성된 랜덤하게 샘플링된 손잡기 시퀀스에 대해 학습된다. 단순화된 모델이 학습된 후 고정된 손잡이 시퀀스에 대한 단순화된 환경에서 참조 궤적을 얻는다. 이후 전체 모델은 task와 스타일 목적 함수를 최적화하면서 단순화된 모델의 참조 궤적을 모방하여 학습된다. 평가 시 단순화된 모델을 planner로 사용하여 전체 손잡이 시퀀스에 대한 선행 또는 잡기별 기준으로 전체 모델에 대한 guidance를 제공할 수 있다. 함께 작동하는 두 모델을 통해 시스템은 표준 RL policy에 어려움이 있는 어려운 손잡이 시퀀스를 통과할 수 있다.
2. Learning Simplified Policies
단순화된 정책은 캐릭터가 다음 손을 잡을 때 주어지는 sparse reward를 최적화하도록 학습된다. 단순화된 policy가 sparse task reward만으로 학습될 수 있다는 사실은 흥미로운 행동이 나타날 수 있도록 하기 때문에 바람직하다. DRL에서 학습이 성공하거나 학습 속도를 크게 높이려면 종종 reward shaping이 필요하다. 동시에 reward shaping은 control policy가 task와 관련 없는 목적 함수에 최적화되고 주요 task에서 벗어나도록 하는 바이어스를 도입할 수도 있다. Sparse reward를 사용하여 policy를 직접 최적화하면 찾기가 매우 어려운 솔루션 mode를 찾을 수 있다.
Simplified Policy Networks
단순화된 policy에는 controller와 value function이라는 두 개의 신경망이 포함된다. Controller와 value function은 출력 레이어에서만 다른 유사한 아키텍처를 가지고 있다. 각 신경망은 256개의 hidden unit과 ReLU activation이 있는 레이어가 3개인 feed-forward 네트워크이다. Action은 PD controller의 proportional gain 상수에 의해 조정되므로 controller 네트워크의 출력 레이어에 Tanh activation을 적용하여 값이 -1과 +1 사이에서 정규화되도록 한다. Value function은 정규화되지 않은 return 기대값에 근접한 스칼라 값을 출력한다. 네트워크에 대한 입력은 앞에서 설명한 것과 같다.
3. Learning Full Model Policies Using Simplified Model Imitation
전체 모델의 policy는 단순화된 모델에서 생성된 참조 궤적을 추적하여 모방 학습을 사용하여 학습된다. 모방 학습은 현재 캐릭터 state와 미래 참조 궤적이 주어진 각 timestep에서 조인트 토크를 생성하기 위해 전체 모델 policy가 필요한 inverse dynamics 문제로 간주될 수 있다. Reward function은 task reward 구성 요소, 보조 reward 구성 요소, 스타일 reward 구성 요소를 갖는 것으로 간주할 수 있다.
단순화된 환경에서와 같이 task reward $r_\textrm{task}$는 다음 타겟 손잡이를 성공적으로 잡은 것에 대한 sparse reward이다. 보조 reward $r_\textrm{aux}$은 tracking 기간과 reaching 기간을 포함하여 학습을 용이하게 하는 reward 항으로 구성된다. Tracking 항은 캐릭터가 참조 궤적을 밀접하게 따르도록 하고 reaching 항은 잡는 손이 다음 타겟 손에 쥐는 위치에 가까워지도록 장려한다. 스타일 reward $r_\textrm{style}$ 항이 추가되어 몸통을 똑바로 세우고 팔 회전을 늦추고 하체 움직임을 줄이고 에너지를 최소화하는 등 보다 자연스러운 움직임을 장려한다. 마지막으로 전체 reward는 다음과 같이 계산할 수 있다.
\[\begin{aligned} r_\textrm{full} &= \exp (r_\textrm{aux} + r_\textrm{style}) + r_\textrm{task} \\ r_\textrm{aux} &= w_t r_\textrm{tracking} + w_r r_\textrm{reaching} \\ r_\textrm{style} &= w_u \textrm{upright} + w_a r_\textrm{arm} + w_l r_\textrm{legs} + w_e r_\textrm{energy} \end{aligned}\]스타일 reward는 학습 결과에 영향을 미치지 않는다. 캐릭터는 스타일 reward 없이 상완 (upright) 동작을 배울 수 있다.
Full Policy Networks
Controller와 전체 모델의 value function은 레이어 너비가 256이고 레이어가 5개인 두 개의 신경망으로 구성된다. Policy의 처음 세 개의 hidden layer는 softsign activation을 사용하고 마지막 두 개의 hidden layer는 ReLU activation을 사용한다. Action을 정규화하기 위해 최종 출력에 Tanh가 적용된다. Critic은 모든 hidden layer에 ReLU를 사용한다. 이전 연구들은 네트워크 크기의 영향과 관련하여 본질적으로 모순되며 전신 모션 모방 작업에 대해 더 나은 성능과 더 나쁜 성능을 모두 제공하기 위해 더 큰 네트워크 크기를 찾는다. 실험에서 저자들은 단순화된 모델에 사용되는 더 작은 네트워크는 전체 환경에서 brachiation task를 학습할 수 없음을 발견했다.
4. Initial State and Early Termination
두 환경 모두에서 첫 번째 손잡이에 90도 각도로 매달려 있는 캐릭터를 초기화한다. 여기서 0도는 진자 정지 위치에 해당한다. 캐릭터의 초기 속도는 기본 상태가 다음 손잡이에 도달하는 데 필요한 전방 모멘텀을 제공하므로 0으로 설정된다.
종료 조건이 충족되면 환경이 재설정되며, 이를 복구 불가 state로 들어가는 것으로 정의한다. 복구 불가 state는 캐릭터가 어떤 손잡이도 잡고 있지 않고 하향 속도로 다음 손잡이의 잡을 수 있는 범위 아래로 떨어지는 경우에 도달한다.
복구 불가 기준 외에도 두 환경 모두 최소 및 최대 잡기 시간을 구현한다. 최소 및 최대 시간은 각각 0.25초 및 4초로 설정된다. 최소 잡기 시간의 아이디어는 잡는 동안 물리적으로 주먹을 형성하는 데 필요한 반응 시간과 시간을 시뮬레이션하는 것이다. 최대 잡기 시간은 사실상 또 다른 형태의 조기 종료 역할을 한다. Policy가 추진력을 생성하는 방법을 이미 학습하지 않은 경우 캐릭터가 복구 불가 state로 들어가도록 강제한다.
Results
- 학습 디테일
- NVIDIA RTX 2070 GPU 1개
- 간단화된 모델의 학습은 5분 소요, 전체 모델은 1시간 소요
- 최대 수집 샘플의 수는 2500만 개로 제한됨
- Learning rate: $3 \times 10^{-4}$에서 시작하여 exponential annealing으로 $3 \times 10^{-5}$까지 감소
- Optimizer: Adam
- Mini-batch size: 2000
1. Simplified Model Results
학습된 control policy는 중요한 비행 단계를 필요로 하고 캐릭터가 필요에 따라 앞뒤로 추가 스윙을 수행하는 비상 펌핑 동작을 나타내는 까다로운 손잡이 시퀀스를 통과할 수 있다. 다음은 펌핑 행동을 시각화한 것이다.

Number of Look-ahead Handholds
다음은 미리 볼 수 있는 손잡이 개수에 대한 간단화된 모델의 실험 결과이다.
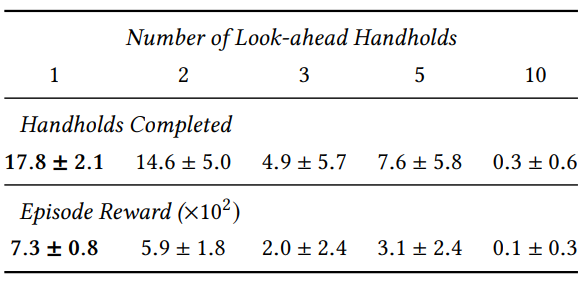
Importance of Early Termination
다음은 조기 종료 전략에 대한 간단화된 모델의 ablation study 결과이다.

2. Full Model Results
저자들은 학습 중에만 단순화된 모델을 사용하는 tracking reward를 사용하는 것 외에도 inference 시 단순화된 모델의 참조 궤적을 추가로 활용하는 세 가지 방법을 실험하였다. 실험에 사용된 모델 구성은 다음과 같다.
- A. Tracking reward only: Tracking reward는 task reward와 결합되어 전체 모델 policy를 학습시킨다. 참조 궤적은 tracking reward를 계산하는 데만 사용된다.
- B. Tracking + Other Rewards: Reward에는 tracking, task, 보조, 스타일 reward와 같은 모든 reward 조건이 포함된다.
- C. Rewards + Release Timing: Reward에는 B의 모든 것이 포함된다. 또한 참조 궤적의 릴리스 타이밍은 전체 모델 policy의 잡기 action을 제어하는 데 사용된다.
- D. Rewards + States: Reward에는 B의 모든 것이 포함된다. 또한 미래 참조 궤적의 일부가 전체 모델 policy 입력의 일부로 포함된다.
- E. Rewards + States + Grab Info.: Reward에는 D의 모든 것이 포함된다. 또한 미래 참조 궤적만으로 전체 모델 state를 컨디셔닝하는 대신 해당 미래 지점에 대한 잡기 flag도 제공한다.
결과는 아래 그래프와 같다.
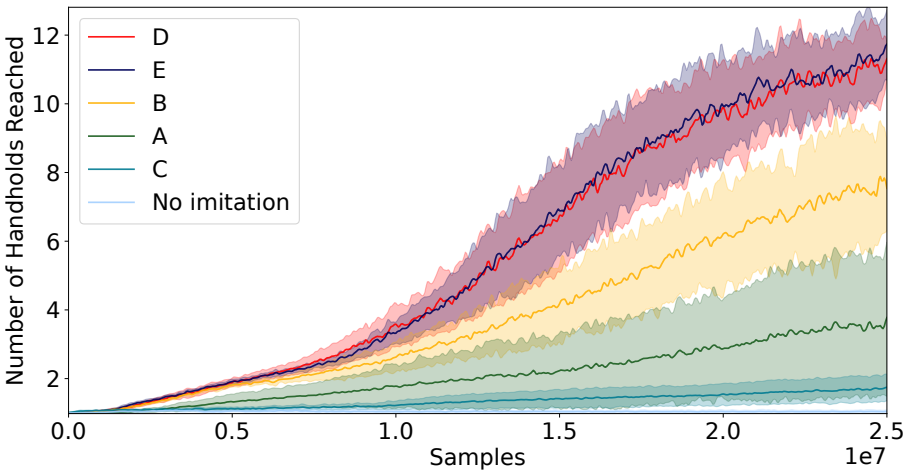
3. Full Model with Planning
Inference 시 단순화된 모델을 사용하여 예상 범위를 확장하여 전체 모델 policy의 능력을 확장할 수 있다. 전체 모델 policy의 value function은 학습에 사용된 예측 손잡이의 수 이상을 예상할 수 없다. 그러나 단순화된 모델은 model predictive control (MPC) 스타일로 손잡이 기반으로 다시 계획할 수 있을 만큼 충분히 빠르다. 런타임에 수천 개의 궤적을 병렬로 시뮬레이션하는 데 사용할 수 있다. 저자들은 미래 4초 동안 1만 개의 궤적을 탐색하도록 planner를 설정했다. 이는 기계 시간의 1초 이내에 완료될 수 있다.
Planner는 전체 모델 policy $\pi_\textrm{full}$, 전체 모델 value function $V_\textrm{full}$, 단순화된 모델 policy $\pi_\textrm{simple}$의 세 가지 완전히 학습된 구성 요소를 사용한다. 이 방법은 손잡이를 놓을 수 있는 인접한 천장 지형을 입력으로 사용한다. 전체 모델 캐릭터의 현재 state $s_t$를 감안할 때 지형 \(\{\mathcal{P}_k\}\)에서 길이가 $K$이고 손잡이 $H$개의 손잡이 계획을 랜덤으로 샘플링한다. 구체적으로, 평면 $\mathcal{P}_k$의 각 손잡이는 이전 손잡이를 넘어 수평 거리 $\delta x \sim \mathcal{U} (1.1, 1.8)$에서 샘플링되고 해당 높이를 지형에서 가져온다. 그런 다음 다음과 같이 정의된 목적 함수에 따라 최상의 계획, 즉 $k = \textrm{argmax } J (\mathcal{P}_k)$를 유지한다.
\[\begin{equation} J (\mathcal{P}_k) = V_\textrm{full} (s_t, k[0:N]) + \sum_j^H R_j \end{equation}\]여기서 $R_j$는 $\pi_\textrm{simple}$로 얻은 단순화된 모델에 대한 reward이고 $N$은 $H > N$인 policy look-ahead 값이다. 그런 다음 선택한 계획은 다음 손잡이에 도달할 때까지 사용되며 이 시점에서 전체 replanning이 발생한다. 이 MPC와 같은 프로세스는 무한히 반복된다. 저자들은 위의 목적 함수가 $\pi_\textrm{simple}$ 또는 $V_\textrm{full}$의 reward만 사용하는 것과 비교하여 더 나은 planning 궤적을 생성한다는 것을 경험적으로 발견했다. 이는 단순화된 모델의 reward가 전체 캐릭터의 feature를 포착하기에 충분하지 않은 반면 value function은 제한된 planning 범위를 갖기 때문이다.
다음은 다양한 planning 방법들에 대한 정량적 평가 결과이다.
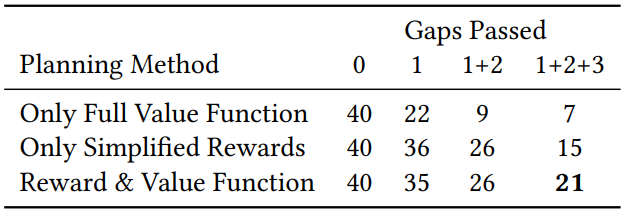
다음은 planner와 함께 policy를 사용할 때 통과하는 지형의 예이다.

(a) 전체 모델 value function만 사용한 planning
(b) 간단화된 모델만 사용한 planning
(c) 전체 모델 value function과 간단화된 모델을 혼합한 planning