[논문리뷰] Binary Latent Diffusion
arXiv 2023. [Paper]
Ze Wang, Jiang Wang, Zicheng Liu, Qiang Qiu
Purdue University | Microsoft Corporation
10 Apr 2023

Introduction
고품질의 새로운 샘플을 효율적으로 생성할 수 있는 이미지 분포 모델링의 목표는 표현 학습 및 생성 모델의 연구를 주도한다. 픽셀 space에서 이미지를 직접 표현하고 생성하는 것은 GAN, flow model, energy 기반 모델, diffusion model 등 다양한 연구를 자극하였다. 해상도가 높아짐에 따라 픽셀 값을 정확하게 회귀하기가 점점 더 어려워진다. 그리고 이 문제는 일반적으로 계층적 모델 아키텍처를 통해 또는 현저하게 높은 비용으로 해결해야 한다. 또한 뛰어난 생성 이미지 품질을 보여주지만 GAN 모델은 불충분한 모드 커버리지와 학습 불안정성 등의 문제를 겪는다.
학습된 latent space에서 이미지를 표현하고 생성하는 것은 유망한 대안을 제공한다. Latent diffusion은 픽셀 space보다 차원이 낮은 latent feature space에서 denoising을 수행하므로 각 denoising step의 비용이 줄어든다. 그러나 실수 latent 표현을 회귀하는 것은 여전히 복잡하며 수백 개의 diffusion step을 필요로 한다. VAE는 반복적인 step 없이 이미지를 생성한다. 그러나 latent space의 정적 prior는 표현력을 제한하고 posterior collapse로 이어질 수 있다.
모델링 복잡성을 크게 증가시키지 않고 latent 분포의 유연성을 높이기 위해 VQ-VAE는 vector-quantized latent space를 도입한다. 여기에서 각 이미지는 학습된 코드북의 벡터를 가리키는 인덱스 시퀀스로 표시된다. 그런 다음 벡터 양자화 표현에 대한 prior는 일반적으로 autoregressive model로 parameterize되는 학습된 sampler에 의해 모델링된다. VQ-VAE의 성공은 가속 병렬 autoregressive model과 multinomial diffusion model과 같은 다른 모델로 코드북 인덱스의 이산적인 latent space를 모델링하는 일련의 연구들을 자극하였다. VQ 기반 생성 모델은 학습 불안정과 같은 문제 없이 GAN과 같은 보다 정교한 방법보다 우수한 놀라운 이미지 합성 성능과 모델 커버리지를 보여준다. 그러나 각 이미지 패치를 나타내기 위해 하나의 코드북 인덱스를 사용하는 엄격한 제한은 코드북 크기에 대한 trade-off를 도입한다. 왜냐하면 더 많은 이미지 패턴을 커버할 수 있을 만큼 충분히 큰 코드북은 sampler에 대해 지나치게 복잡한 multinomial latent distribution를 도입할 것이기 때문이다.
본 논문에서는 각 이미지 패치가 이제 binary 벡터로 표현되며, 이산적인 binary latent code로 prior가 맞춤형으로 개선된 binary diffusion model에 의해 효과적으로 모델링되는 binary latent space에서 이미지의 콤팩트하면서도 표현적인 표현을 탐색한다 베르누이 분포용. 특히, 이미지와 binary 표현 간의 양방향 매핑은 binary latent space를 가지는 feed-forward autoencoder에 의해 모델링된다. 이미지가 주어지면 인코더는 이제 독립적으로 분산된 베르누이 변수 시퀀스의 정규화된 파라미터를 출력한다. 여기에서 이 이미지의 binary 표현이 샘플링되고 이미지를 재구성하기 위해 디코더에 공급된다. 베르누이 분포의 불연속 샘플링은 자연스럽게 기울기 전파를 허용하지 않는다. 저자들은 높은 학습 효율성을 유지하면서 고품질 이미지 재구성에 간단한 straight-through gradient copy가 충분하다는 것을 발견했다.
Binary latent space에 컴팩트하게 표현된 이미지를 사용하여 이미지의 binary latent code에서 prior를 모델링하여 새로운 샘플을 생성하는 방법을 소개한다. 기존의 많은 생성 모델의 단점을 극복하기 위해 랜덤 베르누이 분포에서 시작하는 denoising 시퀀스를 통해 새로운 샘플의 binary 표현을 생성하는 binary diffusion model을 도입한다. 베르누이 분포로 모델링된 binary latent space에서 diffusion을 수행하면 가우시안 기반 diffusion process에서와 같이 대상 값을 정확하게 회귀할 필요성이 줄어들고 더 높은 효율로 샘플링이 가능하다. 그런 다음 각 denoising step에서 예측 대상을 입력과 원하는 샘플 사이의 residual로 점진적으로 reparametrize하고 제안된 binary latent diffusion model을 학습시켜 학습 및 샘플링 안정성을 개선하기 위해 이러한 ‘flipping 확률’을 예측하는 방법을 소개한다.
Binary Image Representations
이미지 데이터셋이 주어지면 이미지와 binary 표현 간의 양방향 매핑을 학습하는 것으로 시작한다. 이는 각 이미지의 binary code가 이미지에서 추론된 독립적으로 분산된 베르누이 변수 시퀀스의 샘플로 획득되는 binary latent space로 autoencoder를 학습시킴으로써 달설된다. 구체적으로, 이미지를 $x \in \mathbb{R}^{h \times w \times 3}$로 나타내면 해당 베르누이 분포 $\Psi (x)$에 대한 정규화되지 않은 파리미터를 출력하는 이미지 인코더 $\Psi$를 학습시킨다. Sigmoid $\sigma$는 파라미터 $y \in \mathbb{R}^{\frac{h}{k} \times \frac{w}{k} \times c} = \sigma(\Psi(x))$를 정규화하기 위해 사용된다. 여기서 $h$와 $w$는 이미지의 공간 해상도를 나타내고 $k$는 인코더 $\Psi$의 downsampling factor이다. $c$는 인코딩된 feature 채널의 수이다.
이미지의 binary 표현을 얻기 위해 정규화된 파라미터 $z = \textrm{Bernoulli}(y)$가 주어지면 베르누이 샘플링을 수행한다. 여기서 베르누이 샘플링 연산은 기울기 전파를 자연스럽게 허용하지 않으며 인코더-디코더 아키텍처의 end-to-end 학습을 막는다. 실제로, 기울기를 직접 복사하고 역전파에서 미분할 수 없는 샘플링을 건너뛰는 straight-through gradient estimation이 안정적인 학습과 우수한 성능을 모두 유지할 수 있다. Straight-through gradient estimation은 다음과 같이 쉽게 구현할 수 있다.
\[\begin{equation} \tilde{z} = \oslash (z) + y - \oslash (y) \end{equation}\]여기서 $\oslash$는 stop gradient 연산이다. $z$와 동등하고 binary인 $\tilde{z}$는 이미지 재구성을 위해 디코더 네트워크 $\Phi$에 보내진다. 디코더 $\Phi$에서 $\tilde{z}$로 다시 전파된 기울기는 $y$로 직접 전송되며, 이는 인코더 $\Psi$에 대해 미분 가능하고 이산적인 binary latent space를 사용하여 전체 autoencoder의 end-to-end 학습을 가능하게 한다.
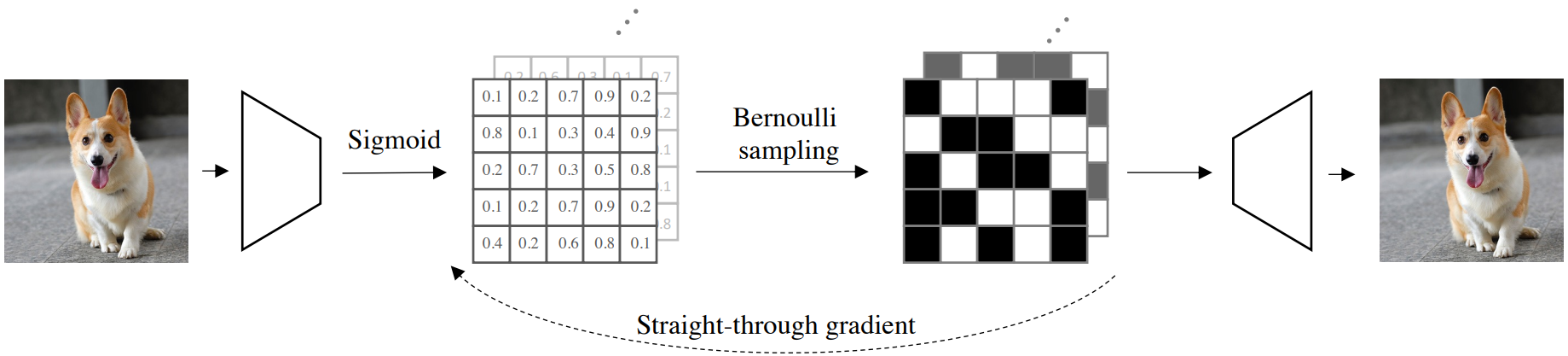
이미지 재구성은 $\hat{x} = \Phi (\tilde{z})$로 얻는다. Binary autoencoder의 전체 프레임워크는 위 그림에 시각화되어 있다. End-to-end 기울기 전파를 보장하는 기울기 함수를 사용하여 네트워크는 다음 최종 목적 함수를 최소화하여 학습된다.
여기서 $\mathcal{C}$는 MSE, perception loss, adversarial loss와 같은 loss function의 모음이다. $\omega_i$는 각 loss 항의 균형을 맞추는 기울기이다.
Bernoulli Diffusion Process
이미지 데이터셋과 각 이미지의 binary latent 표현이 주어지면 parameterize된 모델 $p_\theta (z)$를 사용하여 binary latent code로 prior을 효과적으로 모델링하는 방법에 대해 논의한다. 여기서 binary latent code의 새로운 샘플을 효율적으로 샘플링할 수 있다. 이를 위해 안정적이고 효과적인 학습 및 샘플링을 촉진하는 개선 기술과 함께 베르누이 분포에 맞게 특별히 조정된 diffusion model인 binary latent diffusion을 도입한다.
Diffusion model은 일반적으로 \(t \in \{1, \cdots, T\}\)에서 일련의 변동 분포 $q(z^t \vert z^{t-1})$로 구성된 $T$단계 diffusion process를 먼저 정의하여 확립된다. $q(z^t \vert z^{t-1})$의 각 변동 분포는 $z^{t-1}$에 noise를 점진적으로 추가하도록 정의되어 충분한 step $T$와 $q(z^t \vert z^{t-1})$를 정의하는 유효한 noise scheduler를 사용하며, 최종 상태 $q(z^T \vert z^0)$는 평가 및 샘플링이 용이하고 $z^0$의 유효한 정보를 거의 전달하지 않는 알려진 랜덤 분포로 수렴한다. 특히 본 논문은 이미지의 binary latent code의 사전 분포를 모델링하는 데 관심이 있다. 따라서 latent code 분포 $z \sim q(z^0)$로 diffusion process의 시작점을 정의한다. 여기서 $q(z^0)$는 latent code의 prior인 베르누이 분포이다. 그리고 전체 diffusion process $q$는 다음과 같이 정의할 수 있다.
\[\begin{equation} q(z^{1:T}) := \prod_{t=1}^T q(z^t \vert z^{t-1}), \quad \textrm{with} \\ q(z^t \vert z^{t-1}) = \mathcal{B} (z^t; z^{t-1} (1-\beta^t) + 0.5 \beta^t) \end{equation}\]여기서 $\mathcal{B}$는 베르누이 분포이고 $\beta^t$는 각 step $t$에서의 noise scale이다. Step $T$가 충분하고 scale $\beta^t$가 적합하면 forward diffusion process는 $\mathcal{B}(z^T; 0.5)$로 수렴할 것이다. 아래 그림은 binary latent diffusion process의 예시이다.
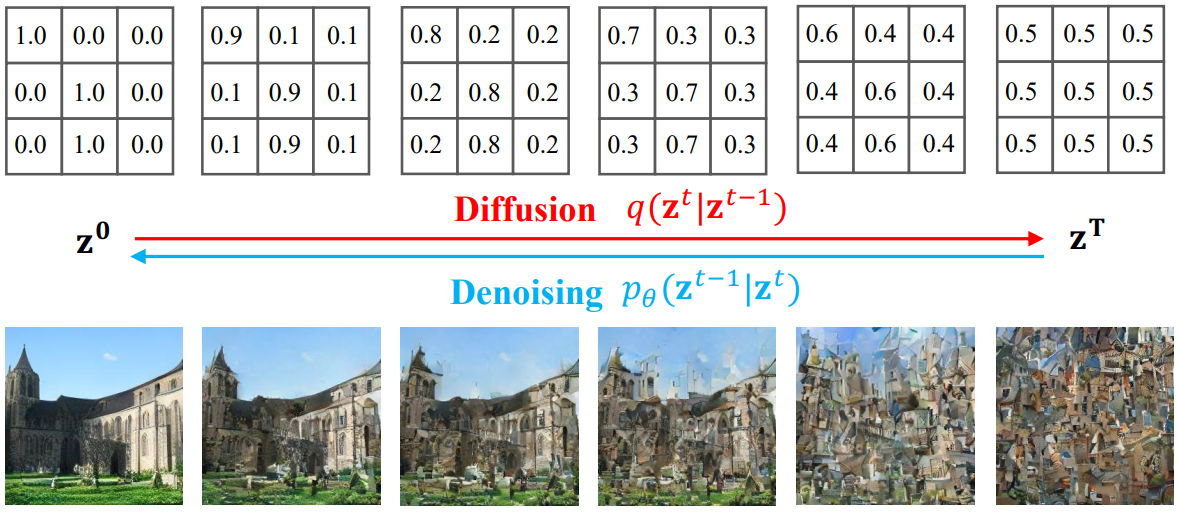
임의의 timestep $t$와 샘플 $z^0$이 주어지면 사후 분포는 다음과 같이 쉽게 얻을 수 있다.
여기서 $k^t$와 $b^t$는 timestep $t$까지 누적된 noise scale을 공동으로 정의한다. Markov chain과 posterior의 수치적 형식은 각 학습 batch에서 확률적 샘플링을 허용한다.
제안된 binary latent diffusion process의 noise scheduler는 각 step에서 noise scale $\beta^t$를 단순히 정의하거나 $k^t$와 $b^t$를 직접 정의하여 구성할 수 있다. $k^t$와 $b^t$를 직접 정의하더라도 해당 $\beta^t$는 여전히
\[\begin{equation} \beta^t = 1 - \frac{k^t}{k^{t-1}} \end{equation}\]로 얻을 수 있다.
Forward diffusion process가 적절하게 정의되었으므로 이제 목표는 $\hat{z}^{t-1} = f_\theta (z^t, t)$로 함수 $f_\theta$를 학습시켜 reverse diffusion process를 모델링하는 것이다.
\[\begin{equation} p_\theta (z^{t-1} \vert z^t) = \mathcal{B} (z^{t-1}; f_\theta (z^t, t)) \end{equation}\]샘플을 $q(z^T)$에서 $q_\theta(z^0)$의 샘플로 reverse하여 샘플링을 수행할 수 있다. Diffusion process $q$와 denoising process $p$는 VLB를 사용하여 VAE를 공동으로 정의한다.
\[\begin{aligned} \mathcal{L}_\textrm{vlb} := \;& \mathcal{L}_0 + \sum_{t=1}^{T-1} \mathcal{L}_t + \mathcal{L}_T \\ = \;& -\log p_\theta (z^0 \vert z^1) \\ &+ \sum_{t=1}^{T-1} \textrm{KL} (q(z^{t-1} \vert z^t, z^0) \;\|\; p_\theta (z^{t-1} \vert z^t)) \\ &+ \textrm{KL} (q(z^T \vert z^0) \;\|\; p(z^T)) \end{aligned}\]본 논문에서는 미리 정의한 고정된 noise scheduler $\beta^t$를 사용하므로 우변의 세번째 항은 $\theta$에 의존하지 않으며 항상 0에 가깝다. 모든 분포가 베르누이 분포를 포함하므로 모든 항을 closed form으로 수치적으로 계산할 수 있다.
1. Binary Latent Diffusion Reparameterization
Reverse diffusion process를 학습하기 위한 간단한 방법은 신경망 $f_\theta$가 $p_\theta (z^{t-1} \vert z^t)$를 모델링하도록 학습시키는 것이다. 각 $z^t$를 $z^0$와 $z^T$의 선형 보간으로 생각할 수 있으며, 파라미터들은 noise scheduler에 의존하여 0과 1 사이의 수를 취할 수 있다. 따라서, $f_\theta$가 $p_\theta (z^{t-1} \vert z^t)$를 모델링하도록 직접적으로 학습하는 것은 모델이 복잡한 보간을 정확하게 회귀해야 하므로 어렵다.
Predicting $z^0$
예측 대상을 $p_\theta (z^0 \vert z^t)$로 reparametrize하는 방법은 각 $t$에 대헤 $f_\theta$가 $z^0$를 $\hat{z}^0 = f_\theta (z^t, t)$로 직접 예측하도록 학습한다. 샘플링 중에는 각 $t$에 대해 예측된 $p_\theta (z^0 \vert z^t)$으로 $p_\theta (z^{t-1} \vert z^t)$를 복구한다.
\[\begin{equation} p_\theta (z^{t-1} \vert z^t) = q(z^{t-1} \vert z^t, z^0 = 0) p_\theta (z^0 = 0 \vert z^t) + q(z^{t-1} \vert z^t, z^0 = 1) p_\theta (z^0 = 1 \vert z^t) \\ \textrm{where} \quad q(z^{t-1} \vert z^t, z^0) = \frac{q(z^t \vert z^{t-1}, z^0) q(z^{t-1} \vert z^0)}{q(z^t \vert z^0)} \end{equation}\]구체적으로, binary code $z^t$와 noise scheduler가 있으면 다음과 같다.
\[\begin{aligned} p_\theta (z^{t-1} \vert z^t) &= \mathcal{B} (z^{t-1} \vert \frac{[(1-\beta^t) z^t + 0.5 \beta^t] \odot [k^t f_\theta (z^t, t) + 0.5 b^t]}{Z}) \\ Z &= [(1-\beta^t) z^t + 0.5 \beta^t] \odot [k^t f_\theta (z^t, t) + 0.5 b^t] \\ &+ [(1-\beta^t) (1-z^t) + 0.5 \beta^t] \odot [k^t (1 - f_\theta (z^t, t)) + 0.5 b^t] \end{aligned}\]여기서 $Z$는 유효한 확률을 보장하는 정규화 항이고, $\odot$은 element-wise product이다. 도입된 reparameterization을 통해 모든 timestep의 예측 대상은 $z^0$이 되며, 이는 엄격하게 binary로 유지되며 학습을 용이하게 한다.
Predicting the residual
예측 대상을 residual로 reparameterize하는 방법은 diffusion과 denoising score matching 사이를 연결하고 샘플링 결과를 개선한다. 제안된 binary latent diffusion에서 감소하는 noise scale은 $t$가 감소함에 따라 $z^t$가 $z^0$에 가까워지는 결과를 가져온다. 따라서 binary latent space의 샘플링은 $t$가 $t = 0$에 가까워질수록 자연스럽게 binary code로의 flipping이 더 적다.
예측에서 이 희소성(sparsity)을 더 잘 포착하고 발산을 방지하여 샘플링을 안정화하기 위해, 예측 대상은 binary latent diffusion에서 $z^0$와 $z^t$ 사이의 residual로 추가 parametrize될 수 있다. 구체적으로 $z^t \oplus ⊕ z^0$에 맞도록 $f_\theta (z^t, t)$를 학습시킨다. 여기서 $\oplus$는 element-wise logic XOR 연산을 나타낸다. 모델 $f_\theta$는 이제 binary code의 ‘flipping 확률’을 예측하도록 학습되었다. 그리고 예측 대상은 엄격하게 binary로 유지된다.
Final training objective
최종 목적 함수는 다음과 같다.
\[\begin{equation} \mathcal{L}_\textrm{residual} = \mathbb{E}_{t, z^0} \textrm{BCE} (f_\theta (z^t, t), z^t \oplus z^0) \end{equation}\]여기서 $\textrm{BCE}(\cdot, \cdot)$은 binary cross-entropy loss이다. 실제로는 최종 목적 함수를 \(\mathcal{L}_\textrm{residual}\)과 \(\mathcal{L}_\textrm{vlb}\)의 결합으로 설정하는 것이 좋다고 한다.
\[\begin{equation} \mathcal{L} = \mathcal{L}_\textrm{residual} + \lambda \mathcal{L}_\textrm{vlb} \end{equation}\]여기서 $\lambda$는 작은 수이다.
Sampling temperatures
실제로 residual $f_\theta (z^t, t)$의 예측은
\[\begin{equation} f_\theta (z^t, t) = \sigma (\mathcal{T}_\theta (z^t, t)) \end{equation}\]로 구현되며, 여기서 $\mathcal{T}_\theta$는 정규화되지 않은 flipping 확률을 출력하는 일반 transformer이며, Sigmoid function $\sigma$로 정규화된다. 샘플링 중에 예측을
\[\begin{equation} f_\theta (z^t, t) = \sigma (\mathcal{T}_\theta (z^t, t) / \tau) \end{equation}\]로 바꾸는 temperature $\tau$를 삽입하여 샘플링 다양성을 수동으로 조정할 수 있다. $\tau$는 학습 후 샘플링 동안 다양성을 조정하는 데만 사용되며 학습에서 hyperparameter로 포함되지 않는다. $\tau$가 샘플 다양성에 미치는 영향의 예는 아래 그림에 나와 있다.

2. Comparisons with Existing Methods
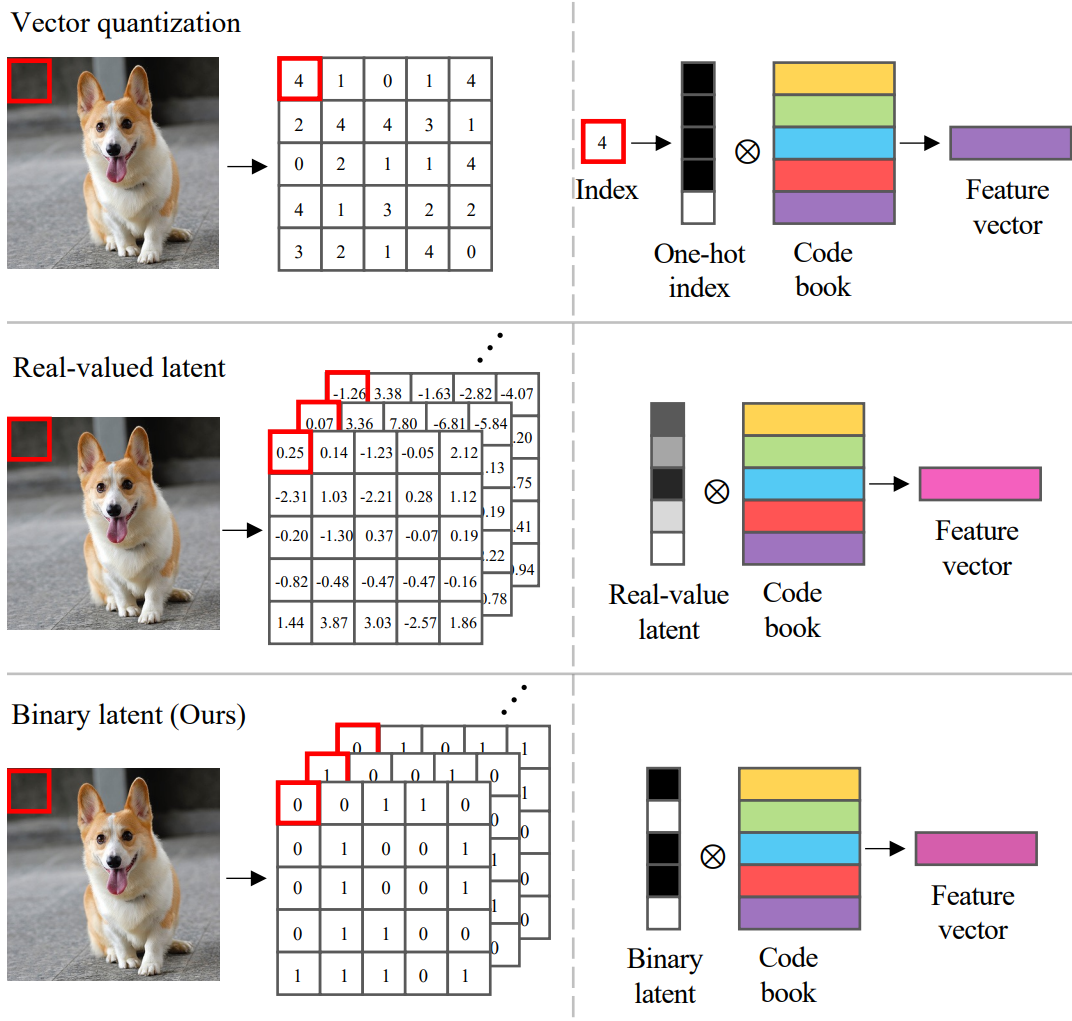
Latent space 이미지 표현의 다른 방벙에 비해 제안된 binary 표현을 채택하는 이점에 대해 간략하게 논의한다. 위 그림에서 볼 수 있듯이 vector-quantized latent space는 각 이미지 패치를 이산적인 인덱스 또는 one-hot vector로 나타낸다. 그런 다음 one-hot vector는 학습된 코드북과 곱하여 이미지 패치의 feature 표현을 얻는다. 연속적인 latent space의 이미지 표현은 단순히 디코더 네트워크의 첫 번째 가중치 행렬을 학습된 코드북으로 취급하여 유사한 방식으로 해석할 수 있다.
이미지 패치의 실수 latent code는 코드북에서 벡터의 임의의 선형 결합을 수행하며 저차원 코드로도 다양한 feature space를 커버할 수 있어 효율성이 높다. Binary 표현을 사용하는 본 논문의 방법은 코드북을 구성하는 벡터를 binary로 제한함으로써 이 두 가지 방법 사이의 균형을 위해 노력한다. 한편으로 코드북의 binary 구성은 VQ 표현에 비해 훨씬 다양하고 유연한 feature 구성을 제공한다. 예를 들어, 소형 32비트 binary 벡터는 VQ 표현에 일반적으로 사용되는 1024개의 패턴보다 훨씬 큰 40억 개 이상의 패턴을 나타낼 수 있다. 이렇게 개선된 패턴 적용 범위는 더 높은 표현력을 허용하고 고품질의 VQ 표현으로는 거의 달성할 수 없는 고해상도 이미지 생성을 가능하게 한다. 반면에 binary 제한은 표현이 간결하게 유지되도록 보장한다. 8k비트 binary 표현은 131k비트 표현을 사용하는 latent diffusion model과 비슷한 성능을 보인다.
Experiments
모든 실험에서 temperature $\tau = 0.9$와 $\lambda = 0.1$을 기본으로 사용한다. Binary latent space의 채널 수의 경우 256$\times$256 unconditional 이미지 생성은 $c = 32$, 256$\times$256 클래스 조건부 이미지 생성과 1024$\times$1024 unconditional 이미지 생성은 $c = 64$를 사용한다.
1. Unconditional Image Generation
다음은 256$\times$256 unconditional 이미지 생성에 대한 정량적 비교 결과이다.
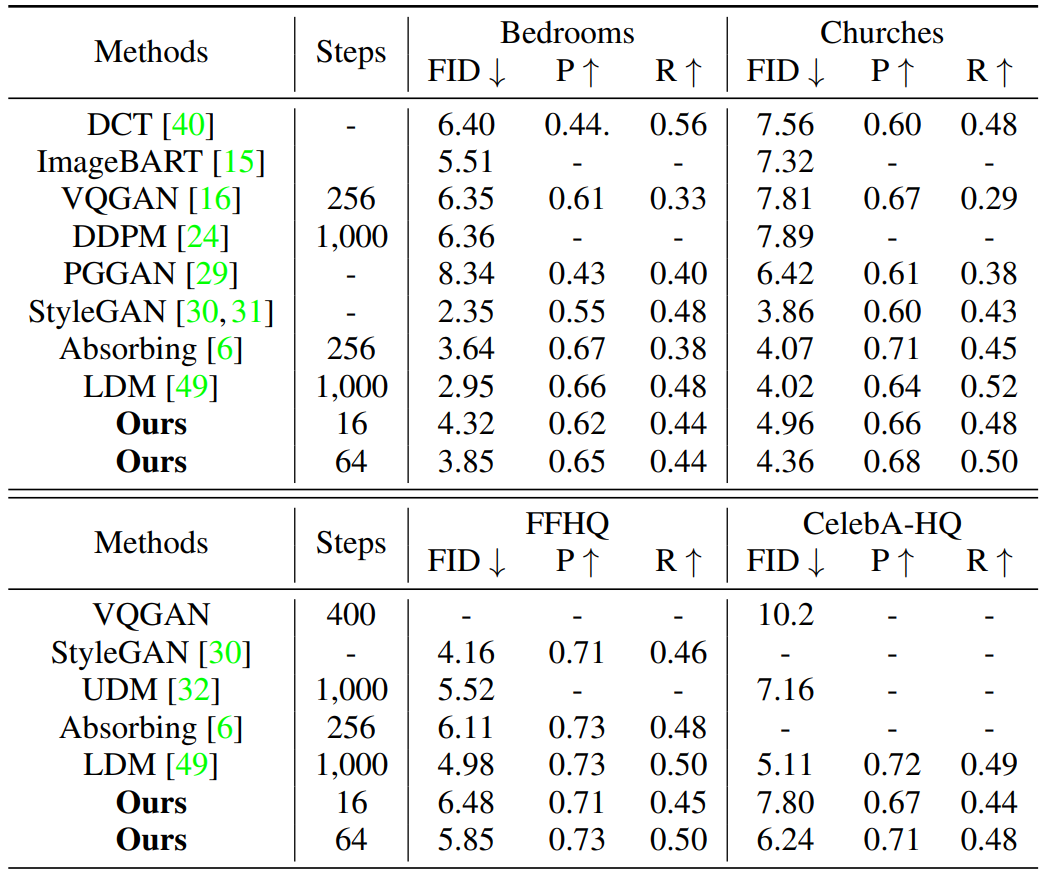
다음은 1024$\times$1024 unconditional 이미지 생성에 대한 정량적 비교 결과이다.
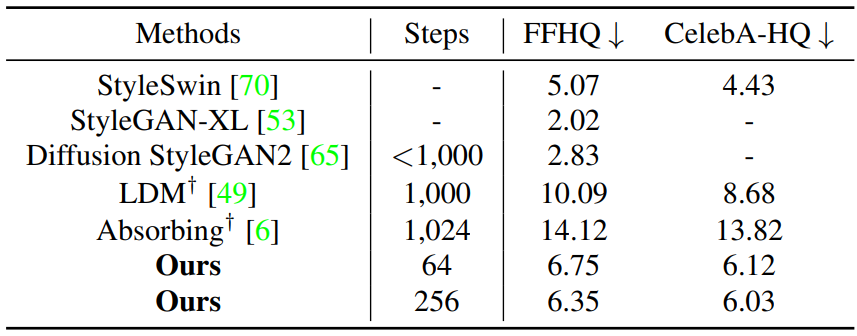
2. Conditional Image Generation
다음은 256$\times$256 클래스 조건부 이미지 생성에 대한 정량적 비교 결과이다.
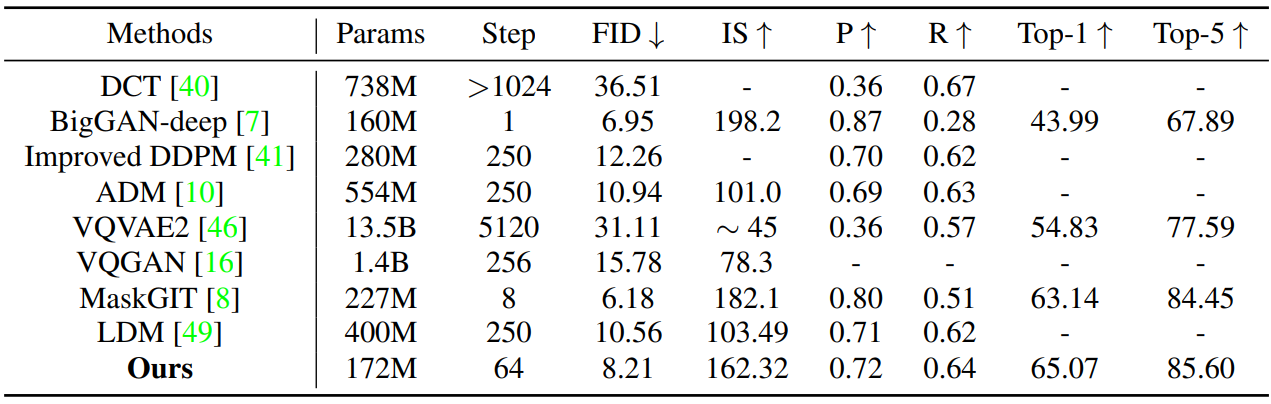
다음은 클래스 조건부로 생성한 이미지 샘플들이다.

3. Discussions
Image Reconstruction
다음은 다양한 latent code의 포맷에 대한 이미지 재구성 품질을 나타낸 표이다.
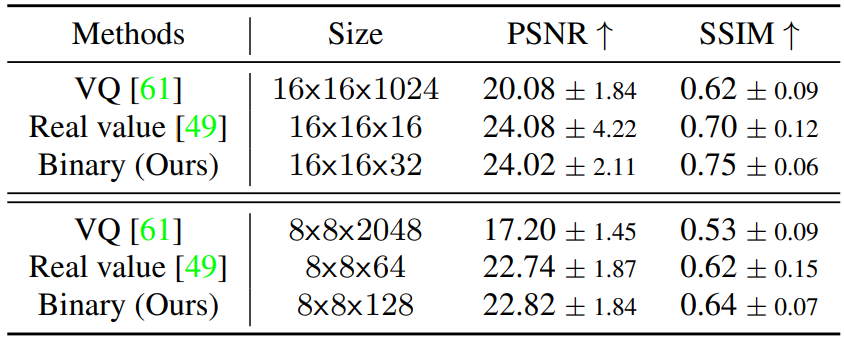
Alternative samplers
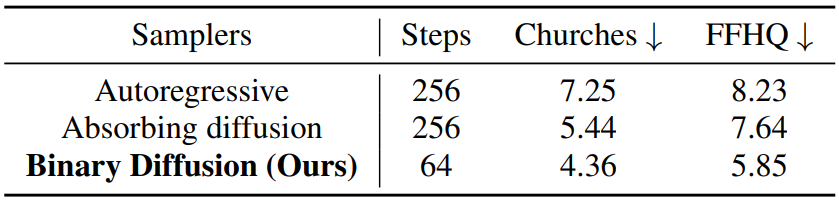
다음은 다양한 sampler로 베르누이 latent 분포에서 prior를 모델링하였을 때의 FID이다.
Efficiency
다음은 이미지 생성 속도를 비교한 표이다. (샘플/초)

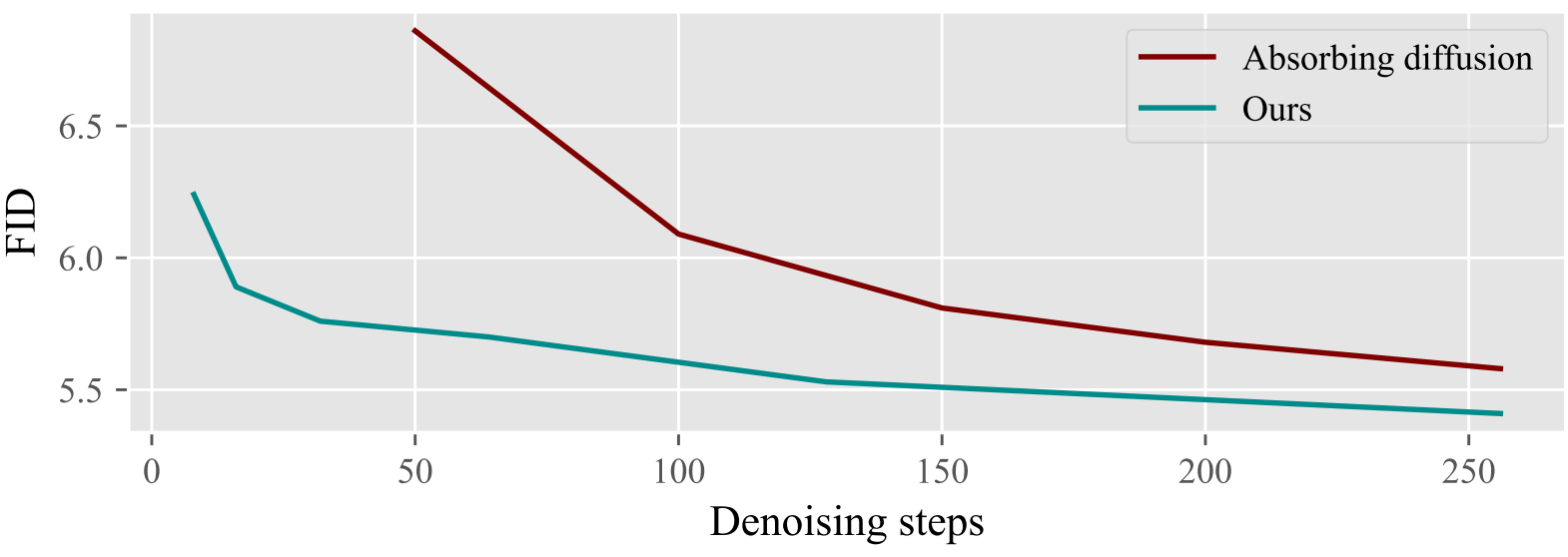
다음은 denoising step에 따른 FID의 변화를 absorbing diffusion model과 비교한 것이다. (공정한 비교를 위해 $\tau = 1.0$)
Ablation studies
다양한 $\lambda$와 예측 대상에 따른 FID와 Recall을 측정한 표이다.

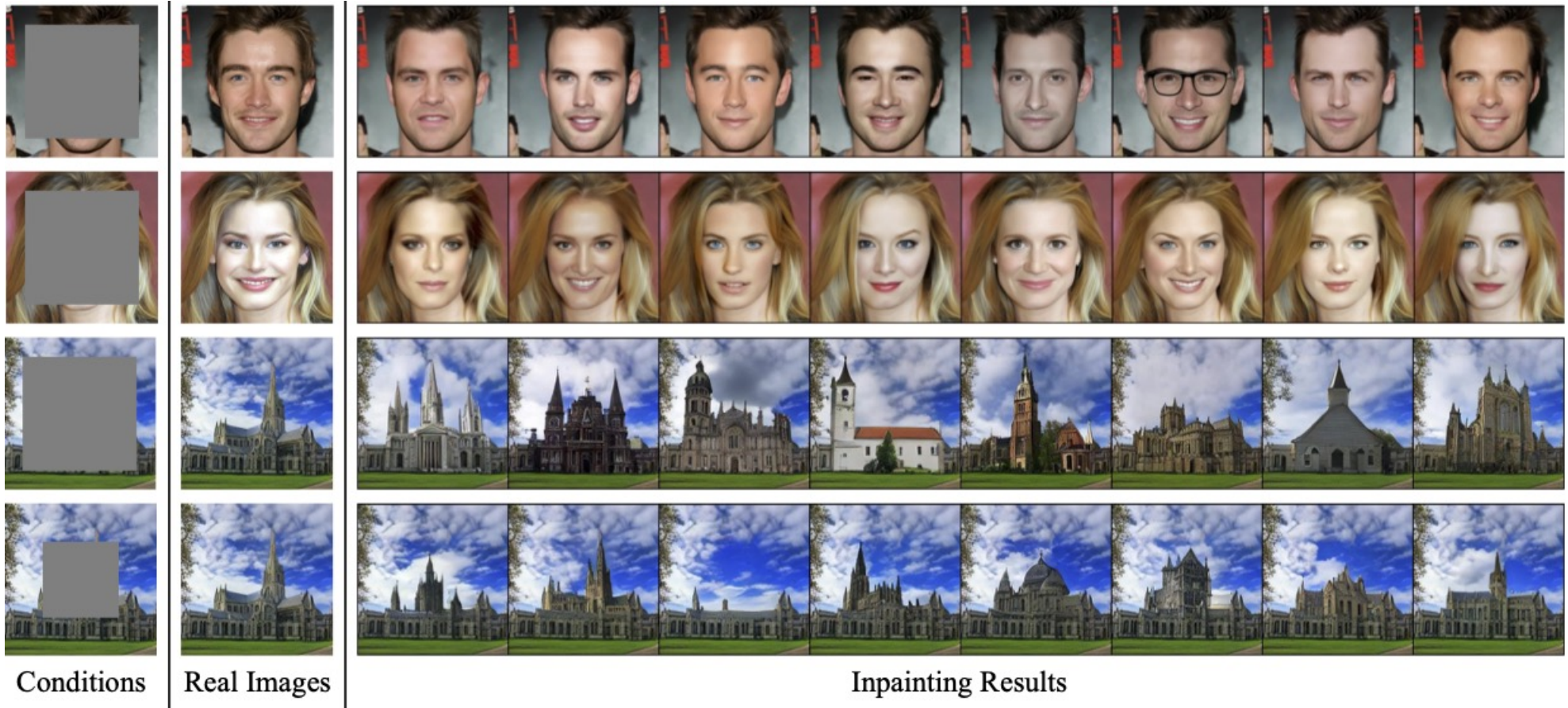
Image inpainting
다음은 inpainting 결과이다.