[논문리뷰] BG-Triangle: Bézier Gaussian Triangle for 3D Vectorization and Rendering
CVPR 2025. [Paper] [Page] [Github]
Minye Wu, Haizhao Dai, Kaixin Yao, Tinne Tuytelaars, Jingyi Yu
KU Leuven | ShanghaiTech University | Cellverse Co, Ltd
18 Mar 2025
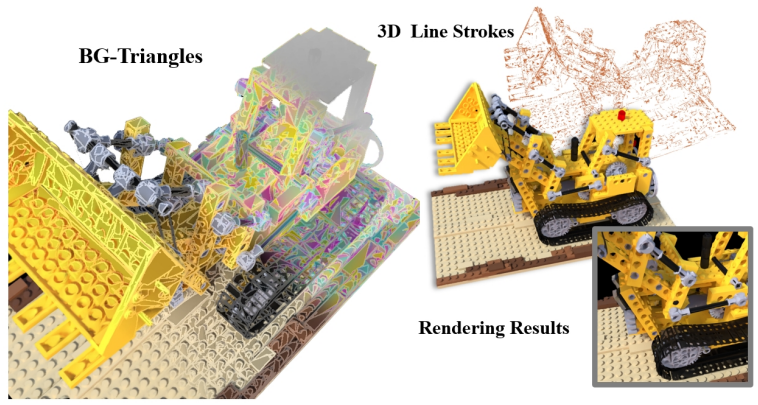
Introduction
3DGS와 NeRF의 주요 한계점은 특히 근접 촬영에서 날카로운 경계를 유지하는 데 어려움을 겪는다는 것이다. 3DGS는 각 Gaussian이 부드럽고 둥근 분포를 가진 3D 공간의 영역을 나타내기 때문에 본질적으로 디테일이 흐릿해지며, Gaussian이 서로 겹쳐지고 섞이기 때문에 모델이 급격한 변화를 포착하는 능력이 제한된다. 마찬가지로 NeRF는 density field의 연속적인 특성으로 인해 빠른 변화를 부드럽게 처리한다. 근본적인 문제는 표현 방식에 있다.
이러한 한계점을 해결하기 위해, 저자들은 명시적으로 정의된 메쉬와 동등한 수준의 확실성을 가지면서도 확률적 모델과 같은 유연성과 미분 가능성을 유지하는 새로운 표현을 찾고자 했다. 본 논문은 Gaussian을 픽셀 레벨 primitive로 사용하는 하이브리드 표현인 Bézier Gaussian Triangle (BG-Triangle)을 제시하였다.
형상 레벨에서는 Bézier 표면을 3D 장면 표현으로 활용하며, 각 primitive는 control point와 속성 집합으로 정의된 장면의 로컬한 표면 영역을 parmeterize한다. 이러한 표면은 rasterization 파이프라인을 지원하고, 속성 버퍼를 생성하고, depth test를 수행하는 등의 연산을 위해 삼각형 메쉬로 테셀레이션될 수 있다. 픽셀 레벨에서는 속성 버퍼를 렌더링 프록시로 사용하여 픽셀 정렬된 Gaussian들을 생성하여 해상도에 무관한 렌더링을 구현한다. 이를 통해 렌더링 중 알파 블렌딩을 통한 시각적 보정이 가능해지고 최적화 중에 부드러운 gradient 계산이 용이해진다.
BG-Triangle을 렌더링하기 위해, splatting을 수행한 후 Gaussian의 각 픽셀에 블렌딩 계수를 할당하여 해당 픽셀이 속한 BG-Triangle primitive의 영향을 반영하는 불연속성 기반의 렌더링 기법을 채택했다. 이 메커니즘은 primitive 영역 외부의 확률적 불확실성을 효과적으로 억제한다. 또한, 저자들은 실시간 성능을 위해 경계 기반의 렌더링 기법을 추가로 개발했다.
저자들은 coarse point cloud 초기화만으로 장면을 재구성할 수 있는 splitting 및 pruning 프로세스를 도입했다. 이 프로세스 덕분에 BG-Triangle은 학습 후에 다양한 수준의 세분성을 가진 물체를 표현할 수 있다. 더 coarse한 레벨에서는 primitive가 동일한 속성 집합을 공유하여 넓은 영역을 표현하므로 정보 활용 효율이 매우 높다. 이러한 효율성 덕분에 매우 적은 수의 primitive로도 고품질 렌더링이 가능하다.
BG-Triangle은 전반적인 렌더링 품질을 저하시키지 않으면서도 선명한 경계를 효과적으로 유지할 수 있다. 특히, 기존 기술로는 구현하기 어려운 세밀한 기하학적 디테일을 확대하여 볼 수 있도록 지원한다. BG-Triangle은 파라미터 효율성과 렌더링 품질/선명도 간의 새로운 trade-off를 이룬다.
Method
1. Bézier Patches
Bézier 삼각형 표면은 Bézier 곡선을 3차원으로 확장하는 표면의 한 유형으로, 삼각형 도메인에서 정의된다. 복잡한 표면과 곡선을 효율적으로 표현하여 기존 메쉬 표현에서처럼 과도한 삼각형 면의 필요성을 줄이며, 잘 정의된 무게중심 좌표계(barycentric coordinate)를 갖는다.
구체적으로, degree $n$의 Bézier 삼각형 $\textbf{S}$는 control point \(\textbf{p}_{i,j,k} \in \mathbb{R}^3\)로 정의된다. 여기서 $i + j + k = n$이고 $i, j, k \ge 0$이다. $u + v + w = 1$이고 $u, v, w \ge 0$인 중심 좌표 $(u, v, w)$를 사용하면 Bézier 삼각형에 있는 점 $\textbf{S}(u, v, w) \in \mathbb{R}^3$은 barycentric interpolation 공식을 통해 고유하게 결정될 수 있다.
\[\begin{equation} \textbf{S}(u,v,w) = \sum_{i=0}^n \sum_{j=0}^{n-i} B_{i,j,k}^n (u,v,w) \textbf{p}_{i,j,k} \\ \textrm{where} \; B_{i,j,k}^n (u,v,w) = \frac{n!}{i! j! k!} u^i v^j w^k \end{equation}\]Bézier 삼각형 표면을 기반으로, Bézier Gaussian triangle (BG-Triangle)을 primitive로 사용한다.
2. Rendering Pipeline
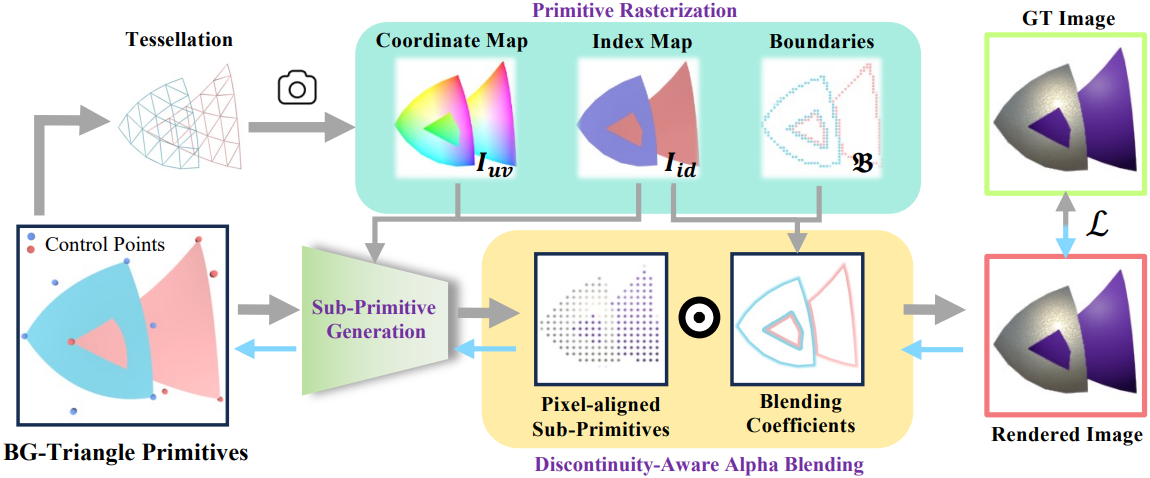
Tessellation and Rasterization
화면 픽셀과 Bézier 삼각형 간의 매핑은 그 공식의 본질적인 비선형성으로 인해 간단하지 않다. 이미지 평면의 픽셀 그리드에 맞추려면 Bézier 삼각형을 곡면에 가까운 더 작은 평면 삼각형으로 테셀레이션해야 한다. 이러한 평면 삼각형의 vertex는 중심 좌표와 primitive의 ID를 포함하여 원래 primitive의 속성 정보를 상속한다.
기존의 rasterization 파이프라인을 사용하여 depth test 후 rasterization된 이미지를 렌더링하고 삼각형 내에서 이러한 속성을 interpolation하여 좌표 맵 \(\textbf{I}_{uv} \in \mathbb{R}^{H \times W \times 3}\)과 인덱스 맵 \(\textbf{I}_{id} \in \mathbb{Z}^{H \times W}\)를 생성한다. 이러한 속성 버퍼는 타겟 뷰의 각 픽셀에 대한 좌표와 primitive ID를 나타낸다. 이웃 픽셀에 다른 primitive ID가 할당된 픽셀은 경계 픽셀로 표시되고 불연속성 기반 렌더링에 사용하기 위해 2D boundary point 집합 $\mathcal{B}$에 저장된다.
Sub-Primitive Generation
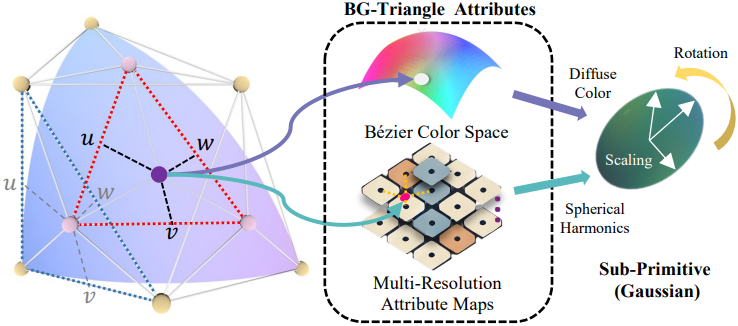
테셀레이션과 rasterization 후, primitive는 장면의 레이아웃 구조와 윤곽을 형성한다. 그러나 이것만으로는 외형을 설명하기에 충분하지 않다. 또한, 렌더링 파이프라인은 미분 가능하지 않다. 따라서 3DGS에서 영감을 받은 Gaussian 기반 확률 모델을 사용하여 이미지 픽셀에 픽셀 정렬된 sub-primitive를 생성한다. 3DGS와 달리, 본 설정에서는 Gaussian이 실시간으로 생성된다. 즉, 서로 다른 뷰에 대한 렌더링의 경우, 동일한 BG-Triangle에서 샘플링된 서로 다른 Gaussian들을 사용하여 렌더링된다.
먼저, $\textbf{S}(u,v,w)$에 대한 식을 사용하여 이미지의 각 전경 픽셀 $\textbf{q}$에 대한 3차원 좌표를 계산한다. 구체적으로, BG-Triangle primitive 인덱스 \(\textbf{I}_{id} (\textbf{q})\)와 그 중심 좌표 \(\textbf{I}_{uv} (\textbf{q})\)를 가져온다. 픽셀 $\textbf{q}$에 대응하는 BG-Triangle의 3차원 좌표 \(\textbf{S}_\textbf{q}\)는 다음과 같다.
\[\begin{equation} \textbf{S}_\textbf{q} (\textbf{I}_{uv} (\textbf{q}), \textbf{I}_{id} (\textbf{q})) = \sum_{i=0}^n \sum_{j=0}^{n-i} B_{i,j,k}^n (\textbf{I}_{uv} (\textbf{q})) \textbf{p}_{i,j,k} (\textbf{I}_{id} (\textbf{q})) \end{equation}\](\(\textbf{p}_{i,j,k} (\textbf{I}_{id} (\textbf{q}))\)는 \(\textbf{I}_{id} (\textbf{q})\)로 인덱싱된 BG-Triangle primitive의 control point)
그런 다음, 이러한 각 좌표점 \(\{\textbf{S}_\textbf{q}\}\)에 3DGS와 유사하게 rotation, scaling, spherical harmonic (SH) 계수 등의 속성을 갖는 Gaussian을 배치한다. 하지만 기하학적 구조는 Bézier 삼각형으로 정의되므로 불투명도는 갖지 않는다. 이러한 sub-primitive의 속성은 색상 control point \(\{\textbf{p}_{i,j,k}^c\}\)와 BG-Triangle의 속성 맵 \(\textbf{M}_h\)를 기반으로 interpolation된다.
동일한 BG-Triangle과 연관된 Gaussian의 diffuse color는 매우 유사하고 부드럽게 변한다고 가정한다. 이는 control point의 기울기 계산 및 최적화에 도움이 된다. 이 속성을 강화하기 위해 위 식과 유사한 기법을 사용한다. 각 색상 control point \(\textbf{p}_{i,j,k}^c \in \mathbb{R}^3\)은 RGB 색상 채널을 나타낸다. Diffuse color \(\textbf{c}_\textbf{q}\)를 interpolation하기 위해 다음 식을 사용한다.
\[\begin{equation} \textbf{c}_\textbf{q} (\textbf{I}_{uv} (\textbf{q}), \textbf{I}_{id} (\textbf{q})) = \sum_{i=0}^n \sum_{j=0}^{n-i} B_{i,j,k}^n (\textbf{I}_{uv} (\textbf{q})) \textbf{p}_{i,j,k}^c (\textbf{I}_{id} (\textbf{q})) \end{equation}\]나머지 속성들은 픽셀의 중심 좌표를 기반으로 하는 다중 해상도 2D 속성 맵을 사용하여 interpolation한다.
\[\begin{equation} \textbf{a}_h (\textbf{q}) = \Theta (\textbf{M}_h (\textbf{I}_{id} (\textbf{q})), \textbf{I}_{uv} (\textbf{q})) \end{equation}\]($\Theta (\cdot, \cdot)$는 2D 텍스처 interpolation 함수, \(\textbf{a}_h (\textbf{q})\)는 Gaussian의 한 속성, \(h \in \{\)rotation, scaling, SH 계수\(\}\)는 각각의 Gaussian 속성)
각 속성들은 렌더링 품질에 따라 민감도가 다르므로, 속성 맵 \(\textbf{M}_h\)에 서로 다른 해상도를 적용한다.
Discontinuity-Aware Alpha Blending
이러한 sub-primitive를 렌더링하기 위해 3DGS를 사용한다. Sub-primitive는 Gaussian 기반이므로, 불확실성으로 인해 렌더링 중 블러링 효과가 발생할 수 있다. 각 BG-Triangle 내에서 부드러운 전환이 보장되므로 내부의 흐릿함으로 인해 시각적 품질이 저하되지 않는다. 그러나 경계 영역에서는 이러한 불확실성을 완화하는 메커니즘이 필요하다. 경계에서 3D Gaussian을 직접 자르면 미분 불가능한 렌더링이 발생한다. 따라서, 불확실성을 줄이기 위해 경계를 부드럽게 하고 경계 근처의 splatting된 sub-primitive에 블렌딩 계수를 적용한다.
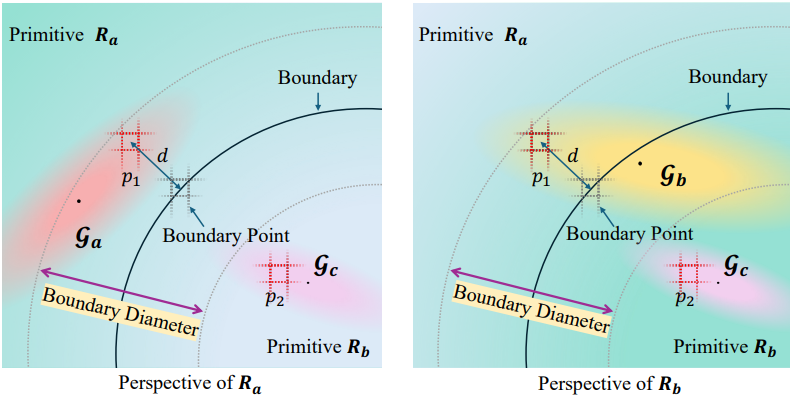
먼저, 이미지에서 경계의 영향 범위를 결정한다. 2차원 boundary point $\mathcal{B}$, \(\textbf{I}_{id}\), \(\textbf{I}_{uv}\)가 주어지면, 대응되는 3차원 boundary point를 유추한다. 각 boundary point는 고정된 scaling factor $r_b$를 갖는 isotropic Gaussian으로 처리된다. 다음으로, 이미지에 projection될 때 이러한 경계 Gaussian의 경계 반경 \(\sigma_i\)를 계산한다. 이는 $i$번째 boundary point \(\textbf{b}_i \in \mathcal{B}\)의 영향 범위를 정의한다. 그런 다음, Gaussian 기반 sub-primitive를 이미지에 splatting하고, splatting된 Gaussian $\mathcal{G}$에 의해 덮인 각 픽셀 $\textbf{q}$에 대한 블렌딩 계수 $w(\textbf{q})$를 다음과 같이 결정한다.
여기서 $g$는 이 Gaussian $\mathcal{G}$가 속하는 primitive의 identifier이고 $\gamma$는 다음과 같이 정의된 블러링 함수이다.
\[\begin{equation} \gamma (d; \sigma) = \min (2^{\frac{d}{\sigma} - 1}, 1) \end{equation}\]이는 거리 $d$를 경계 반경 $\sigma$ 내로 매핑하여, $w (\textbf{q})$ 식이 경계 영역 내에서는 블렌딩 계수를 1.0에서 0.0으로 전환하는 동시에 경계 영역 외부에서는 명확하게 정의되도록 한다.
마지막으로, 픽셀 $\textbf{q}$에서 Gaussian $\mathcal{G}$에 대한 경계의 영향을 완화하기 위해, 알파 값 $\alpha (\textbf{q})$를 기여도 $w (\textbf{q})$와 블렌딩하면 다음과 같다.
\[\begin{equation} \alpha (\textbf{q}) = o \cdot w (\textbf{q}) \cdot e^{-\frac{1}{2} (\textbf{q} - \mu)^\top \Sigma^{-1} (\textbf{q} - \mu)} \end{equation}\]($o$는 최적화를 돕기 위해 1.0에 가까운 상수, $\mu$와 $\Sigma$는 $\mathcal{G}$에서 projection된 2D 위치와 2D 공분산 행렬)
그런 다음, 포인트 기반 알파 블렌딩을 적용하여 픽셀의 최종 색상을 얻는다.
Rendering Acceleration
블렌딩 계수 $w(\textbf{q})$를 계산하기 위해서는 모든 sub-primitive와 각 픽셀에 대해 $\mathcal{B}$의 각 boundary point를 반복하여 결과를 계산해야 때문에 계산 복잡도가 매우 높다. 따라서 $w(\textbf{q})$를 계산할 때 타일 기반 렌더링 알고리즘을 사용한다. 이 알고리즘은 이미지 공간을 여러 타일로 나누고 각 boundary point의 영향을 받는 타일의 범위를 미리 계산한다. 그런 다음 관련 타일로 검색 범위를 제한하여 가장 큰 영향을 미치는 boundary point, 즉 가장 작은 $\gamma$ 값을 생성하는 boundary point를 찾는다. 특정 primitive ID에 속하는 boundary point를 빠르게 찾기 위해 각 타일 내의 boundary point를 ID별로 정렬한다. 이렇게 하면 이진 탐색을 사용하여 목표점을 효율적으로 찾을 수 있다.
3. Training and Optimization
3DGS와 유사하게 BG-Triangle은 미분 가능 렌더링을 직접 지원하며, 3DGS와 동일한 photometric loss를 사용한다.
\[\begin{equation} \mathcal{L} = (1 - \lambda) \mathcal{L}_2 + \lambda \mathcal{L}_\textrm{D-SSIM} \end{equation}\]($\lambda = 0.2$)
Primitive가 겹치거나 세밀한 구조에 맞추기 위해 지나치게 큰 primitive를 사용하는 경우에 최적화가 어려워진다. 이를 해결하기 위해, 저자들은 BG-Triangle에 맞춰 splitting과 pruning 기법을 제안하였다.
Splitting
분할할 primitive를 선택하는 기준은 두 가지이다.
- 학습 뷰에서 control point의 gradient 크기
- Edge prior
Control point 집합의 평균 gradient 값이 크다는 것은 해당 primitive에 상당한 조정이 필요함을 나타내며, 이는 종종 재구성이 부족한 기하학적 구조 때문이다. 따라서 더 세밀한 디테일에 더 잘 맞도록 평균 gradient가 \(\tau_g\)보다 높은 primitive를 분할한다.
Edge prior 측면에서는 학습 이미지에 edge detection을 적용하여 edge gradient를 추출하고, 이 gradient 값을 해당 primitive에 back-projection한다. Primitive에 누적된 edge gradient가 특정 threshold \(\tau_b\)를 초과하면 primitive를 분할한다.
Pruning
비효율적인 primitive를 제거하면 학습 효율을 향상시킬 수 있다. 제거해야 할 primitive를 식별하기 위해 세 가지 기준을 사용한다.
- Primitive의 visibility (primitive가 학습 뷰에서 보이는 비율)
- Primitive의 면적
- Primitive의 종횡비
Experiments
1. Initial Validations
다음은 두 합성 데이터에 대하여 BG-Triangle의 효과를 테스트한 결과이다.
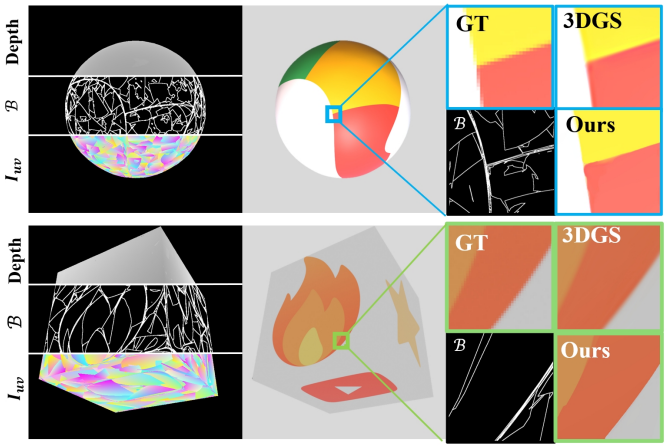
2. Comparisons
다음은 마스킹한 Tank & Temples 데이터셋과 NeRF Synthetic 데이터셋에서 다른 방법들과 비교한 결과이다.
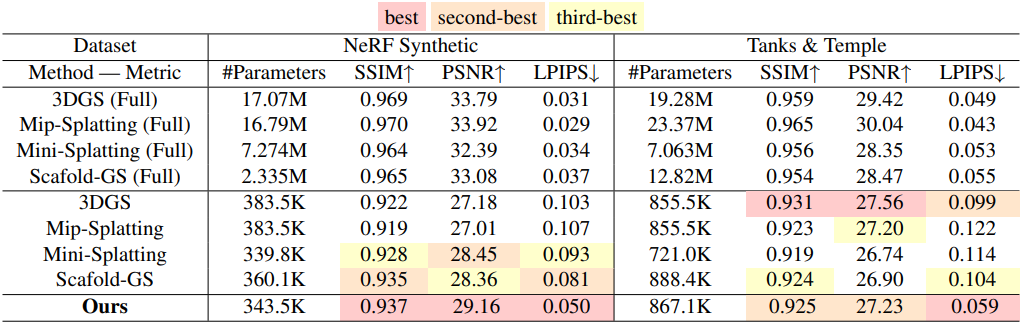


다음은 클로즈업한 뷰에서의 결과를 비교한 것이다. (NeRF Synthetic)
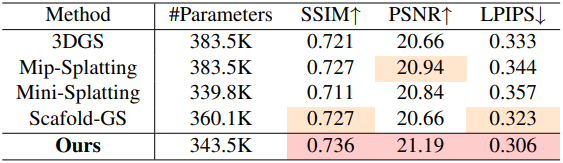
3. Ablation Study
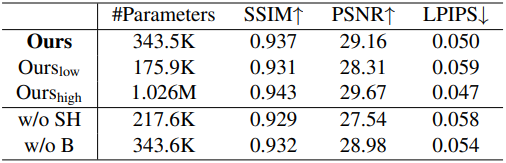
다음은 ablation study 결과이다.
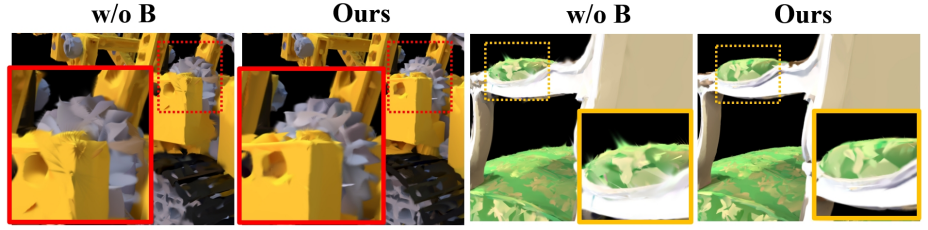
다음은 클로즈업한 뷰에서의 ablation study 결과이다.
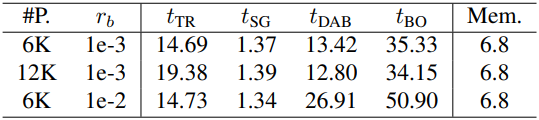
다음은 필요한 메모리와 iteration 당 학습 시간(ms)을 나타낸 표이다. (전체 iteration 수 = 30,000)