[논문리뷰] Deformable Beta Splatting

SIGGRAPH 2025. [Paper] [Page] [Github]
Rong Liu, Dylan Sun, Meida Chen, Yue Wang, Andrew Feng
University of Southern California
27 Jan 2025

Introduction

3DGS의 한계는 주로 기본 구성 요소의 제약에서 비롯된다. Gaussian 커널은 명시적 표현을 통해 실시간 렌더링을 지원하지만, 본질적으로 매끄럽고 흐릿한 결과를 생성해 날카로운 모서리나 평평한 표면 표현에 어려움이 있어 디테일과 사실감이 저하된다. 또한, Gaussian 커널의 긴 꼬리와 무한한 특성은 하드 코딩된 cutoff를 필요로 하며, 이는 아티팩트를 발생시키고 세밀한 기하학적 표현을 더욱 저해한다.

또한, 3DGS는 낮은 차수의 Spherical Harmonics (SH)를 사용하여 시점에 따라 달라지는 색상 정보를 인코딩한다. SH는 조명 변화를 모델링할 수 있지만, 높은 SH 레벨은 파라미터 수가 급증해 실시간 처리에 부적합하다. 결과적으로 3DGS는 낮은 SH 레벨에 의존하게 되고, 이는 단순한 색상 전환과 specular highlight 표현의 한계를 초래한다. Gaussian 커널과 SH 모두 고정 함수 기반이라 다양한 장면과 조명 조건에 적응성이 부족해 시각적 충실도에 한계를 보인다.

이러한 단점을 해결하기 위해, 본 논문에서는 기하학적 표현과 색상 표현을 모두 향상시키도록 설계된 Deformable Beta Splatting (DBS)을 제안하였다. DBS의 핵심은 베타 분포에서 영감을 받은 베타 커널로, 값이 0이 아닌 범위가 유한하며, 유연한 형상 제어를 제공한다. 베타 커널은 다양한 장면 복잡도에 자연스럽게 적응하며, 평평한 표면, 날카로운 모서리, 매끄러운 영역을 높은 정밀도로 표현할 수 있다.

저자들은 색상 표현을 위해 Spherical Beta (SB) 함수를 도입했다. SB는 난반사(diffuse) 성분과 정반사(specular) 성분을 분리하여, 날카로운 specular highlight와 고주파 조명 효과를 효과적으로 모델링할 수 있다. 차수가 3인 SH와 비교할 때, SB는 파라미터 수를 31% 수준으로 줄이면서도 더 뛰어난 성능을 보인다.

또한, 저자들은 3DGS-MCMC의 Markov Chain Monte Carlo (MCMC) 원리를 DBS 프레임워크에 맞게 재정의하고 확장하였다. 기존 3DGS의 밀도 제어 및 3DGS-MCMC의 확률 보존 밀도화 전략은 Gaussian 커널을 기반으로 설계되어, 베타 커널에 직접 적용하기 어려운 문제가 있다. 이를 해결하기 위해, 저자들은 수학적으로 opacity만 조절하면 커널 종류나 densification 횟수와 관계없이 분포를 보존할 수 있음을 증명하였다. 이로써 커널에 구애받지 않는 MCMC 전략이 가능해지며, 복잡한 휴리스틱이나 스케일 재계산 없이 최적화 및 densification 과정을 간소화할 수 있다. 추가로, opacity 제약 조건과의 수학적 일관성을 유지하기 위해 MCMC에서 사용하는 noise function도 베타 커널에 맞게 새롭게 정의하였다.

DBS는 모든 벤치마크에서 3DGS 기반 및 NeRF 기반 방식보다 일관되게 우수한 성능을 보여주었다. 또한, DBS는 3DGS에 필요한 파라미터의 45%만 사용하면서도 3DGS-MCMC보다 1.5배 빠르게 렌더링할 수 있다.

Method

1. The Beta Kernel

베타 커널은 베타 분포에서 파생되며, 이는 입력 $x \in [0, 1]$에 대하여 다음과 같이 정의된다.

\[\begin{equation} f(x; \alpha, \beta) = \frac{1}{\textbf{B}(\alpha, \beta)} x^{\alpha - 1} (1 - x)^{\beta - 1} \end{equation}\]

($\textbf{B}$는 정규화를 위한 베타 함수, $\alpha, \beta > 0$은 모양 제어 파라미터)

매끄러운 3D 뷰 일관성을 촉진하는 종 모양을 얻기 위해 $\alpha = 1$로 고정한다. 정규화 항을 제거함으로써 베타 분포를 베타 커널로 단순화할 수 있다.

\[\begin{equation} \mathcal{B}(x; \beta) = (1 - x)^\beta, \quad x \in [0, 1], \, \beta \in (0, \infty) \end{equation}\]

$\beta$를 직접 최적화하면 커널이 저주파 표현 쪽으로 편향될 수 있다. $\beta$가 0에 가까워질수록 베타 커널은 저주파를 강조하는 반면, 고주파 형태는 $\beta \rightarrow \infty$를 요구하기 때문이다. $\beta$의 적절한 범위를 유지하면서 편향 없는 최적화를 위해, exponential activation을 사용하여 $\beta$를 다시 정의한다. 또한, 베타 커널이 처음에는 Gaussian 형태를 닮아가다가 점차 다양한 형태를 학습하도록 적응하기를 원하기 때문에, $b = 0$일 때

\[\begin{equation} \int_0^1 (1 - x)^{ce^b} dx \approx \int_0^1 e^{-\frac{9x}{2}} \end{equation}\]

가 되는 상수 $c = 4$를 사용한다. 이렇게 하면 $b$가 0으로 초기화될 때 커널이 Gaussian과 유사해진다.

결과적으로, 베타 커널을 다음과 같이 정의된다.

\[\begin{equation} \mathcal{B} (x; b) = (1 - x)^{4e^b}, \quad x \in [0, 1], \, b \in \mathbb{R} \end{equation}\]

베타 커널이 Gaussian과 유사한 형태로 시작하도록 보장하고 최적화 과정에서 그 형태를 조정할 수 있도록 한다. 이를 통해 초기 $\beta$ 값을 수동으로 fine-tuning할 필요가 없어져 베타 커널이 Gaussian 커널의 더욱 유연한 상위 집합이 된다.

2. 3D Ellipsoidal Beta Primitive

3D Ellipsoidal Beta Primitive를 파라미터 집합으로 정의한다.

\[\begin{equation} B = \{\boldsymbol{\mu}, o, \textbf{q}, \textbf{s}, b, \textbf{f} \} \end{equation}\]

여기서 primitive의 중심 좌표 \(\boldsymbol{\mu} \in \mathbb{R}^3\), 불투명도 $o \in [0, 1]$, rotation을 나타내는 quaternion $\textbf{q} \in [-1, 1]^4$, scale \(\textbf{s} \in [0, \infty)^3\)는 3DGS의 파라미터와 동일하다.

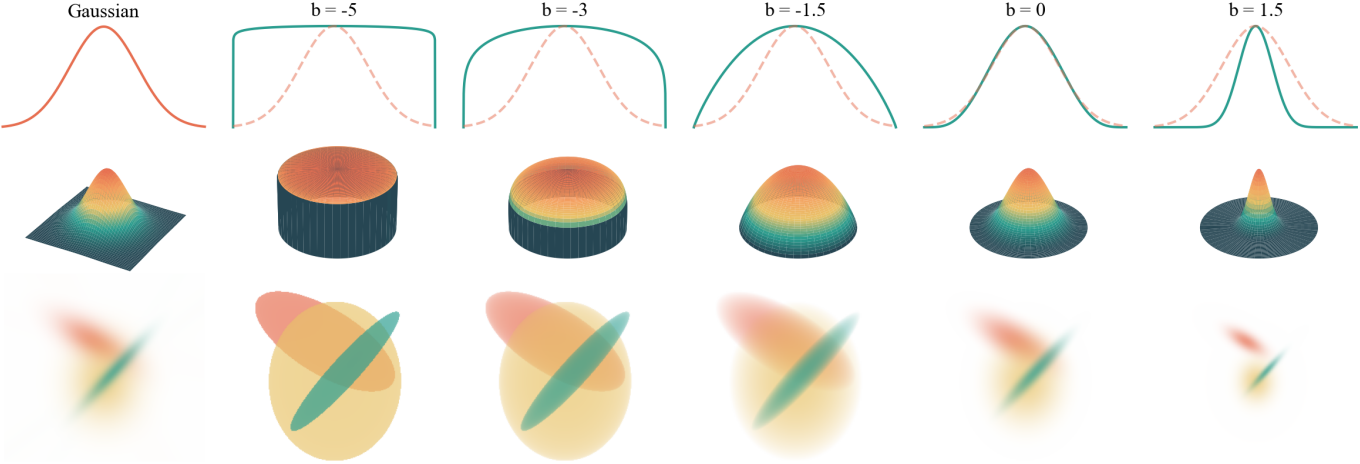
​​파라미터 $b \in \mathbb{R}$를 변경하면 커널 모양이 변형되며, $b = 0$일 때 Gaussian 함수와 거의 동일한 함수가 생성된다. 최적화가 진행됨에 따라 커널이 Gaussian 함수와 유사한 모양에서 더 날카로운 모서리와 평평한 표면을 포착할 수 있는 모양으로 동적으로 조정될 수 있도록 한다.

외관 모델링을 위해 각 primitive는 시점에 따라 달라지는 색상 정보를 인코딩하는 feature 벡터 $f \in \mathbb{R}^d$를 갖는다. 이 벡터는 복잡한 조명 상호작용을 표현하는 데 필수적이다.

픽셀 $\textbf{x} \in \mathbb{R}^2$의 렌더링 과정은 다음과 같다. 각 primitive는 viewing transformation $\textbf{W}$를 사용하여 2D 이미지 평면에 projection된다. 그 결과 2D projection 중심 \(\boldsymbol{\mu}^\prime \in \mathbb{R}^2\)와 이에 대응하는 2D 공분산 행렬

\[\begin{equation} \boldsymbol{\Sigma}^\prime = \textbf{JW}\boldsymbol{\Sigma}\boldsymbol{W}^\top \boldsymbol{J}^\top \quad \textrm{where} \; \boldsymbol{\Sigma} = \textbf{RSS}^\top \textbf{R}^\top \end{equation}\]

그런 다음 픽셀과 각 primitive 중심 사이의 거리를 계산한다.

\[\begin{equation} r_i (\textbf{x}) = \sqrt{(\textbf{x} - \boldsymbol{\mu}_i^\prime)^\top \boldsymbol{\Sigma}_i^{\prime -1} (\textbf{x} - \boldsymbol{\mu}_i^\prime)} \end{equation}\]

카메라를 기준으로 깊이에 따라 겹치는 primitive를 정렬한 후, 정렬된 집합 \(\mathcal{N} = \{B_1, \ldots, B_N\}\)에 대해 베타 커널을 사용하여 최종 픽셀 색상 \(\textbf{C}(\textbf{x})\)에 대한 기여도를 합성한다.

\[\begin{equation} \textbf{C}(\textbf{x}) = \sum_{i=1}^N \textbf{c}_i o_i \mathcal{B} (r_i (\textbf{x})^2; b_i) \prod_{j=1}^{i-1} (1 - o_j \mathcal{B} (r_j (\textbf{x})^2; b_j)) \end{equation}\]

3. Spherical Beta

3DGS는 시점에 따른 색상을 인코딩하기 위해 Spherical Harmonics (SH)를 사용한다. 차수가 $N$인 SH의 경우, feature 차원은 $3(N+1)^2$가 되어 파라미터의 수가 $N$의 제곱에 비례하여 증가한다. 실시간 성능을 위해 3DGS는 $N = 3$인 낮은 차수의 SH를 사용해야 하는데, 이는 부드러운 색상만 제공하고 선명한 specular highlight를 효과적으로 모델링하는 데 어려움을 겪는다. 이 문제를 해결하기 위해 Phong Reflection Model에서 영감을 받은 Spherical Beta (SB) 함수를 도입한다. Phong Reflection Model은 다음과 같이 정의된다.

\[\begin{equation} c(\hat{V}) = A_m + \sum_{m \in \mathcal{M}} [D_m + (\hat{R}_m \cdot \hat{V})^{\alpha_m} c_m] \end{equation}\]

($\hat{V}$는 정규화된 뷰 방향, $A_m$은 주변광, $D_m$은 diffuse color, \(\hat{R}_m\)은 정규화된 반사 방향, \(\alpha_m\)은 반사도를 제어하는 광택 계수)

SB는 주변광과 diffuse color를 하나의 base color $c_0$로 병합한 다음, 학습 가능한 베타 커널을 통해 specular lobe를 직접 모델링한다.

\[\begin{equation} c(\hat{V}) = c_0 + \sum_{m \in \mathcal{M}} \mathcal{B} (1 - \hat{R}_m \cdot \hat{V}; b_m) c_m \end{equation}\]

각 primitive에 대해, 반사되어 나가는 radiance를 모델링하는 $M = \vert \mathcal{M} \vert$개의 SB lobe를 도입한다. 각 SB lobe는 반사 방향 \(\hat{R}_m\), 색상 $c_m$, 광택도 $b_m$로 paramertize되기 때문에, feature $\textbf{f}$의 차원은 $3 + 6M$이며, specular lobe 수에 따라 선형적으로 증가하여 SH보다 효율적이다.

SB는 반사도 모델링 측면에서 Spherical Gaussian (SG)과 유사하지만, SG와 달리 \(\hat{R}_m \cdot \hat{V} = 0\)일 때 radiance의 불연속성이 발생하며 radiance가 0이 된다. 이를 통해 cutoff와 관련된 아티팩트를 제거하면서 radiance의 연속성을 유지한다.

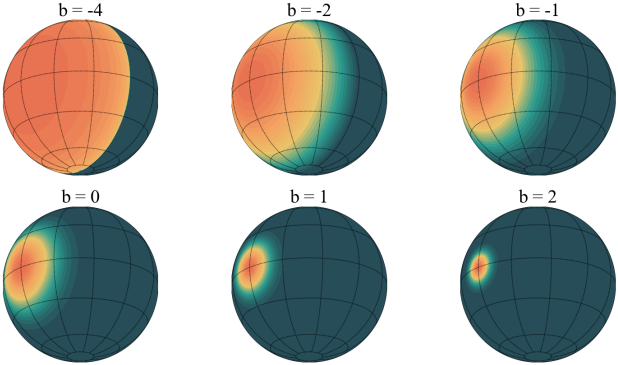
위 그림은 다양한 $b_m$ 값에 대한 specular highlight와 그에 해당하는 specular lobe를 보여준다. SB는 고주파 및 저주파 반사도를 모두 모델링할 수 있으며, 더 적은 파라미터로 복잡한 조명 상호작용과 반사 효과를 모델링할 수 있다.

4. Kernel-Agnostic Markov Chain Monte Carlo

3DGS-MCMC는 각 primitive의 불투명도를 확률로 처리하여 3DGS의 최적화를 Markov Chain Monte Carlo (MCMC) 과정으로 재정의하였다. 불투명도가 pruning threshold 미만인 죽은 Gaussian을 식별하고, 불투명도 값을 기반으로 multinomial sampling을 통해 죽지 않은 Gaussian으로 재배치하여 다시 생성한다. 불투명도와 scale을 모두 조정함으로써, densification 과정에서 기본 확률 분포를 보존하여 프로세스를 안정화한다. 또한, 위치 noise를 도입하여 탐색을 촉진하고 overfitting을 방지하였다.

그러나 이러한 휴리스틱 전략과 scale 조정은 본질적으로 Gaussian 함수의 속성과 연결되어 있어 임의의 커널에 직접 적용하기 어렵다. 이러한 한계를 해결하기 위해, 본 논문은 3DGS-MCMC에서 구축된 프레임워크를 기반으로 Kernel-Agnostic MCMC를 제안하였다.

최적화

탐색을 촉진하고 overfitting을 방지하기 위해, 최적화 과정에서 primitive들의 위치를 ​​교란하는 noise 항 $\epsilon$을 채택한다. 그러면 primitive의 위치 $\boldsymbol{\mu}$는 다음과 같이 업데이트된다.

\[\begin{equation} \boldsymbol{\mu} \leftarrow \boldsymbol{\mu} - \lambda_\textrm{lr} \cdot \nabla_\boldsymbol{\mu} \mathcal{L} + \lambda_\epsilon \epsilon, \quad \epsilon = \lambda_\textrm{lr} \cdot \mathcal{B} (o_i; b^\prime) \cdot \Sigma_\eta \end{equation}\]

($b^\prime = \textrm{ln}(25)$)

저자들은 3DGS-MCMC의 logit noise function을 베타 커널 함수로 대체하여 더욱 간결하고 명확하게 정의된 noise function을 구현했다.

Beta primitive를 학습시키기 위해 다음과 같은 loss function을 사용한다.

\[\begin{equation} \mathcal{L} = (1 - \lambda_\textrm{SSIM}) \mathcal{L}_1 + \lambda_\textrm{SSIM} \mathcal{L}_\textrm{SSIM} + \lambda_o \sum_i \vert o_i \vert + \lambda_\Sigma \sum_i \sum_j \vert \sqrt{\textrm{eig}_j (\Sigma_i)} \vert \end{equation}\]

Opacity regularizer \(\lambda_o \sum_i \vert o_i \vert\)는 커널에 독립적인 densification을 보장하고 primitive의 탐색을 장려한다. \(\lambda_\Sigma \sum_i \sum_j \vert \sqrt{\textrm{eig}_j (\Sigma_i)} \vert\)는 opacity regularizer와 함께 primitive의 소멸과 재생성을 촉진한다.

Densification

불투명도를 정규화하고 조정하는 것이 복제된 primitive의 수나 선택된 splatting 커널에 관계없이 효과적이고 유효함을 수학적으로 증명할 수 있다. 불투명도가 $o$인 splatting 커널 $f(x)$로 정의된 primitive 1개를 $N$개로 복사한다고 가정하면, $N$개의 새로운 primitive 뒤의 알파 블렌딩 가중치가 기존 primitive 1개일 때와 동일해야 하므로, opacity를 $o^\prime$으로 정규화해야 한다.

\[\begin{equation} (1 - o^\prime)^N = 1 - o \\ o^\prime = 1 - (1 - o)^{1/N} \end{equation}\]

여기에 $f(x)$를 통합하면 primitive 중심을 넘어선 보존, 특히 경계에서의 보존이 복잡해진다. 3DGS-MCMC는 Gaussian 커널에 맞춰 scale 조정을 통해 경계 보존을 처리했는데, 이는 복잡하고 변형 가능한 커널들에는 직접 적용할 수 없다.

그러나 저자들은 정규화된 작은 $o$ 값이 주어졌을 때 Taylor expansion을 사용하여 $o^\prime$을 근사화할 수 있음을 발견했다.

\[\begin{equation} o^\prime = 1 - (1 - o)^{1/N} \approx \frac{o}{N} \end{equation}\]

이제 densification된 분포를 고려해 보면 다음과 같다.

\[\begin{equation} 1 - \left( 1 - o^\prime f(x) \right)^N \approx 1 - \left( 1 - \frac{o}{N} f(x) \right)^N \end{equation}\]

$\frac{o}{N} f(x)$도 작으므로 이항 근사를 적용하면 다음과 같다.

\[\begin{aligned} 1 - \left( 1 - o^\prime f(x) \right)^N &\approx 1 - \left( 1 - \frac{o}{N} f(x) \right)^N \\ &\approx 1 - \left( 1 - N \cdot \frac{o}{N} f(x) + \mathcal{O} (o^2) \right) \\ &= o f(x) + \mathcal{O} (o^2) \end{aligned}\]

따라서 원래 분포 $o \cdot f(x)$와 일치한다. 오차항 $\mathcal{O} (o^2)$는 opacity regularizer를 사용하기 때문에 무시할 수 있게 된다. 따라서 복사 횟수 $N$과 splatting 커널 $f(x)$에 관계없이 불투명도를 정규화함으로써 원래 분포와 densification된 분포 간의 차이가 줄어든다.

Experiments

1. Results and Comparisons

다음은 다른 방법들과 렌더링 품질을 비교한 결과이다.

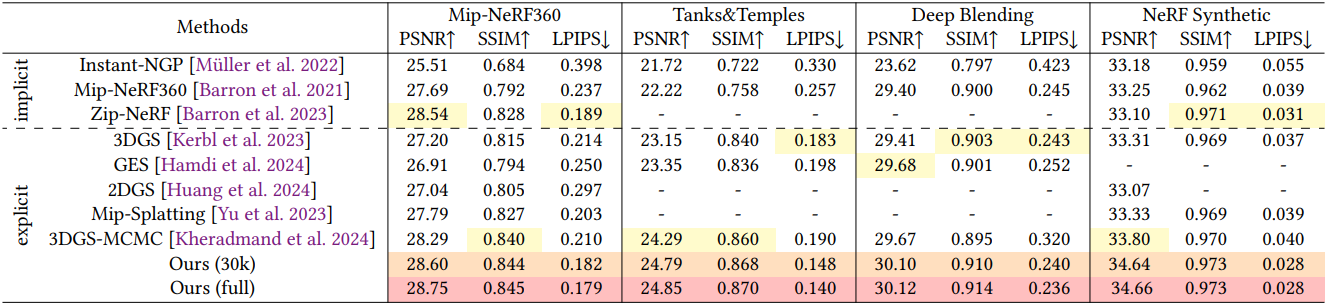
다음은 학습 및 렌더링 효율성을 비교한 결과이다.

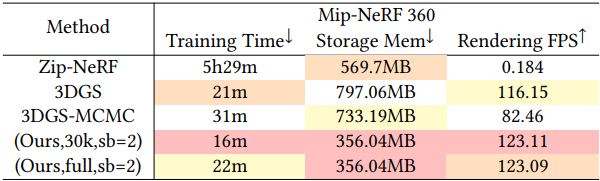
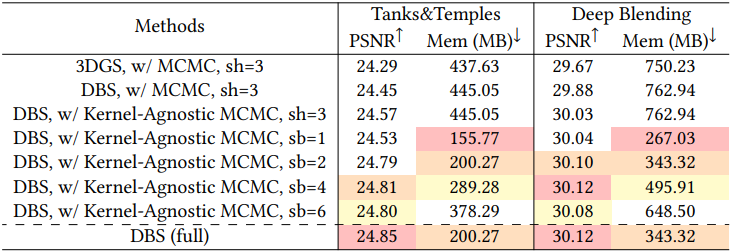
2. Ablation Study

다음은 ablation study 결과이다.

3. Beta Decomposition

다음은 장면 형상을 구조와 디테일로 분리한 결과이다.

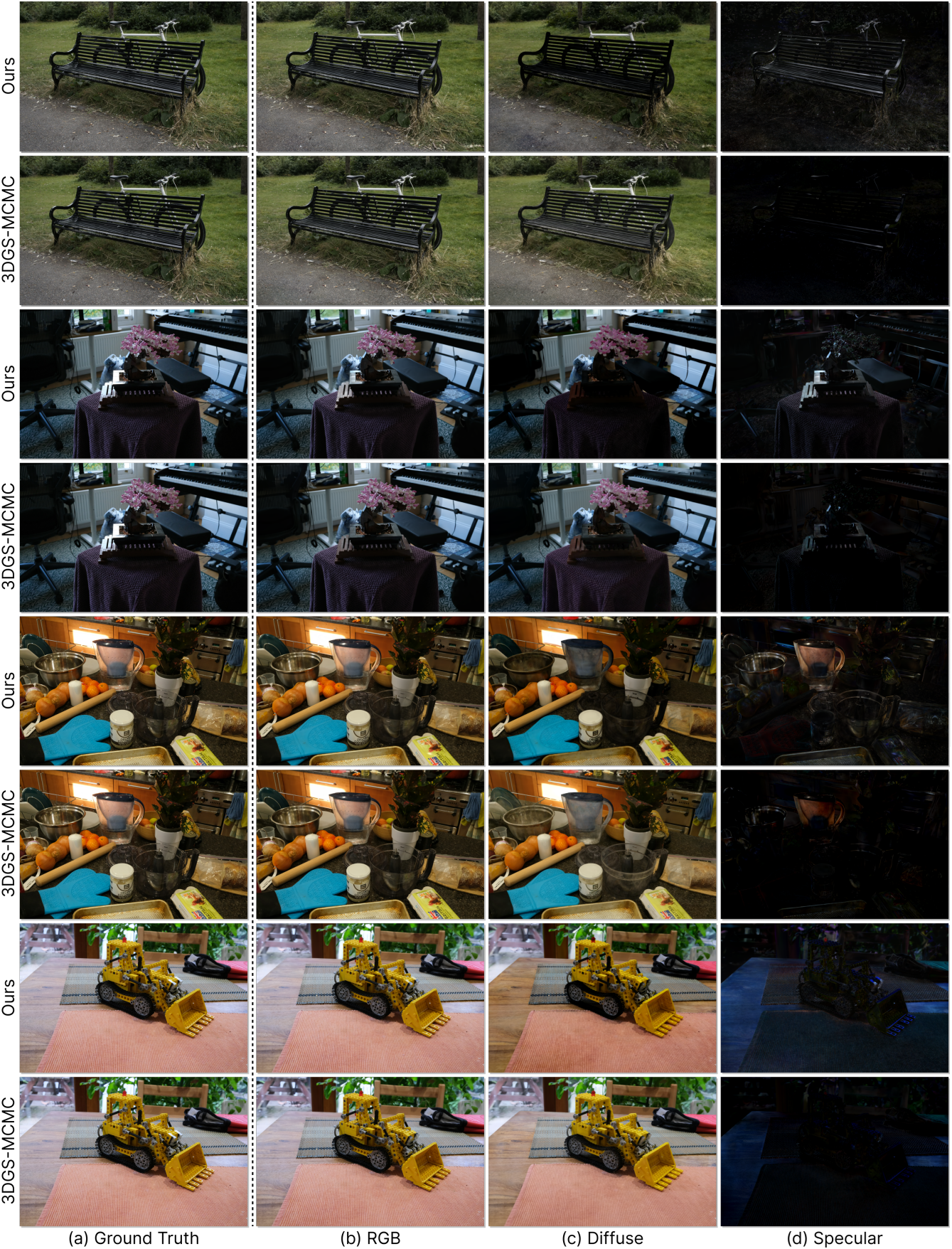
다음은 장면을 diffuse 성분과 specular 성분으로 분리한 결과이다.

Limitations

1. 프레임워크는 rasterization 기반이므로 정렬 과정에서 깊이 근사 부정확성으로 인해 때때로 popping 아티팩트가 발생한다.
2. SB 함수는 거울과 같은 반사와 anisotropic specular highlight를 효과적으로 모델링하는 데 어려움을 겪는다.
3. Frustum model은 베타 커널이 멀리 떨어진 배경에 대해 평평한 형상을 최적화하도록 하여 전반적인 형상 분포에 영향을 미친다.